齿轮成形磨削加工热力耦合数值仿真研究

韩江(1963-),男，河南洛阳人，博士,合肥工业大学教授,博士生导师;

夏链(1964-),女,四川乐山人，博士,合肥工业大学教授,硕士生导师.

齿轮成形磨削加工热力耦合数值仿真研究

张魁榜,韩江,夏链,杨清艳

(合肥工业大学 机械与汽车工程学院,安徽 合肥230009)

摘要:齿轮成形磨削加工为齿轮精加工工艺,在高速成形磨削加工过程中,会产生大量的热。一方面这些磨削热会在齿轮表面产生较高的温度,容易引起工件表面烧伤;另一方面磨削热会在工件表层产生梯度变化较大的温度场,从而形成磨削残余应力,造成工件表层金相组织变化,既会影响齿轮磨削加工的精度,也会影响齿轮使用的寿命。文章借助工程分析软件Abaqus和Matlab,基于磨削移动热源理论和三角形热源分布模型,通过磨削接触长度计算,建立了齿轮成形磨削三维温度场仿真模型;利用热-力耦合分析方法,得到齿轮磨削热应力和应变的数值仿真云图,实现齿轮成形磨削加工温度场及热变形的精确分析,对提高齿轮成形磨削加工精度具有一定的理论意义。

关键词:成形磨齿加工;有限元模型;温度场;热力耦合

收稿日期：2014-07-18；修回日期：2014-11-13

基金项目：国家重大科技专项资助项目(2012ZX04001021)

作者简介：张魁榜(1987-),男,湖北黄石人，合肥工业大学讲师;

doi:10.3969/j.issn.1003-5060.2015.10.001

中图分类号:TG580

Numerical simulation of thermo-mechanical

coupling of gear form grinding process

ZHANG Kui-bang，HAN Jiang，XIA Lian，YANG Qing-yan

(School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:Gear form grinding,which is commonly used for gear finish machining, can greatly improve the precision of gears. But during the process of high speed form grinding, it will produce large amounts of heat. This grinding heat will generate a high temperature on the surface of the gear that will cause the surface burns, and will produce larger varying temperature gradient field on the work-piece surface, thus forming the residual stress of grinding and causing the work-piece surface microstructure changes, which will affect the precision of gear grinding and the service life of the gear. In this paper, by using the engineering analysis software Abaqus and Matlab, the three-dimensional temperature field simulation model of gear form grinding is established based on the theory of moving grinding heat source and triangular heat distribution model and the calculation of grinding contact length. The numerical simulation cloud chart of gear grinding heat stress and strain is gotten by using the thermal-mechanical coupled analysis method, achieving the accurate analysis of the gear form grinding temperature field and thermal deformation. The study has theoretical significance for improving the precision of gear form grinding.

Key words:gear form grinding; finite element model; temperature field; thermo-mechanical coupling

随着现代化工业快速发展,通过计算机辅助制造提升零件加工质量成为重要手段。汽车变速箱和飞机变速箱等对齿轮精密加工要求越来越高,齿轮的高精密磨削已经成为一种必然趋势,其主要特点是减少齿轮磨削过程中的齿面误差,从而减少齿轮传动过程中的噪声并提高使用寿命。

目前工业上齿轮成形磨削精度一般能够达到DIN3962 3级,可以满足一般齿轮传动的精度要求,但对于高精密传动部件还需要提高齿轮磨削加工精度。文献[1]采用VC++编程仿真分析了成形磨削深度对齿轮磨削精度的影响,结果表明可以通过控制磨削深度来提高齿轮成形磨削精度;文献[2]通过对成形砂轮截形偏移、砂轮安装角度误差、砂轮与工件的中心距误差及砂轮修整等因素进行分析,找到了影响齿轮成形磨削精度与各误差间的基本规律;文献[3]对齿轮成形磨削几何误差模型进行了理论建模,对激光干涉仪测量的成形磨齿机几何误差结果进行了补偿,提高了齿轮成形磨削精度。

齿轮成形磨削过程中砂轮与工件接触面大,在磨削加工时需要很高的能量来去除材料[4],这些能量大部分会转化成热量,一部分被冷却液带走,一部分进入砂轮,还有一部分会进入工件,使工件表面温度升高,可能导致工件表面烧伤、降低疲劳强度,从而严重影响工件表面质量和使用寿命[5]。有关研究结果表明[6],在精密加工中,由热变形所引起的制造误差占总制造误差的40%～70%,因此磨削温度场对齿轮的加工质量、机械与传动性能等将产生直接影响。国内外学者对磨削热进行了大量研究。Jaeger最早在1942年提出了磨削加工移动热源理论模型[7]，这个模型首次被文献[8]应用在磨削过程中,即磨削接触区沿着磨削方向在工件表面作热源移动,并假设磨削热主要产生在磨削接触面上;文献[9]认为热模型中应该忽略接触区表面摩擦力,提出了进入工件的磨削热能量比例公式;贝季瑶在1964年提出了三角形热源分布模型[10],这种模型被大多数学者所采用,一直沿用至今。

1成形磨齿加工原理

齿轮成形磨削方法是利用成形砂轮磨削齿轮的渐开线齿形,在磨削直齿外齿轮和直齿内齿轮时,砂轮的轴线垂直于齿轮的轴线,砂轮截形的中心线和砂轮齿槽的中心线相重合,因此砂轮的截形就相当于齿轮齿槽的截形。成形砂轮磨齿没有展成运动,磨齿的精度主要取决于砂轮的修整精度与砂轮的定位精度。当磨削直齿轮时,砂轮的轴向截面形状即为工件的端面齿形;当磨削斜齿轮时,砂轮的轴向截面形状为砂轮与工件理论齿面的空间接触线在砂轮轴向平面的投影。成形砂轮磨齿采用单齿分度时,是不连续的成形磨削,工件轴向进给来实现全齿宽的磨削。磨斜齿轮时,在工件轴向进给的同时,还应作附加的旋转运动,以获得相应的螺旋角。

采用不连续成形法磨削时,砂轮截面形状应和齿轮相一致,齿轮成形磨削方法有3种——砂轮单齿面工作、双齿面工作和三齿面工作,如图1所示。

图1　齿轮成形磨削方法

从图1中可以看出,三齿轮磨削接触面积最大,有3个面相接触,三齿面磨削方法加工时效率最高,但是最易出现磨削热过高,造成磨削烧伤。因此本文对齿轮成形三面磨削进行热仿真分析。

齿轮成形磨削主要优势有:① 砂轮与工件齿面接触面大(沿整个齿面),单位面积承受磨削力较小;② 磨削中采用大磨削量、较低的磨削进给速度;③ 砂轮与工件磨削接触线和啮合线不重合(呈交叉),传动时平稳、噪音低;④ 成形磨齿机可以提高齿轮磨削精度,标准验收精度为DIN3962 3级,如有特殊要求可达DIN3962 1~2级,齿面成形磨削表面粗糙度比展成法磨削有明显提高;⑤ 通过修整砂轮,可以完成齿顶、齿根、齿向及鼓形齿修形。

磨削烧伤缺陷是成形砂轮磨削齿轮工艺中的主要问题,若此问题有效解决,成形砂轮磨齿工艺则可得到更广泛的应用。磨削区的磨削热,不仅影响到工件,也影响砂轮的使用寿命,因此,研究齿轮磨削区温度分布状况,是齿轮磨削机理的重要问题。鉴于齿轮磨削加工的特殊性,确立正确的磨削热模型是研究磨削热分析的关键所在。

2齿轮成形磨削三维热模型

由齿轮成形磨削原理可知,齿轮成形磨削从砂轮轴向界面看,近似于平面磨削,而且磨削参数(包括进给速度、进给量、砂轮材料、工件材料)都可以和平面磨削一样,只有磨削包络接触面不同,因此从原理上,齿轮成形磨削和平面磨削机理一致。由于齿轮磨削在实际中温度很难准确测量,因此本文将平面磨削热分析理论应用到齿轮磨削过程中,以避免齿轮磨削过程中温度精确测量的难题。

2.1齿轮磨削三维建模

砂轮磨削过程可被描述成工件磨削表面上移动热源三维瞬态热传导问题,建立齿轮三维模型和笛卡尔坐标系，如图2所示,热量q加载在磨削平面S1、S2和S3上,沿着砂轮进给方向移动,计算区域内瞬态温度场的导热微分方程如下:

(1)

其中，ρ为合金钢4140密度;Cp为导热系数;Ω为工件传热区域。

S1、S2、S3边界条件分别为:

(2)

(3)

(4)

其他表面则有:

(5)

初始条件为:

(6)

其中,T0为实验室温度,初始值为20 ℃。

根据成形法的磨削原理,采用间歇分度加工法进行磨齿加工,同时磨削齿轮的1个齿的齿槽及2个齿的齿面,可认为每个轮齿的磨齿温度分布基本相同。因此,在Abaqus中建立磨齿有限元分析模型,将齿轮沿齿宽方向即Z轴方向分为80等分,沿齿高方向即X轴方向分为8等分,靠近磨削平面处更密,采取规则的8节点6面体参元的有限元单元,采用扫略等方法进行网格划分。载荷加载在一个齿的齿槽部分,齿槽的左齿面和齿根上的面,即图2中的S1、S2和S3面。

图2　成形磨削齿轮三维模型

2.2移动热源分布模型

由于齿轮成形磨削时,砂轮沿着工件表面移动,磨削而产生的热源也以同样的速度沿工件移动,与平面磨削非常接近,因此平面磨削的理论同样适合齿轮的成形磨削加工。根据Jaeger移动热源理论,建立齿轮磨削加工移动热源理论模型,进行齿轮成形磨削热数值仿真分析。在Abaqus中将磨削过程分为80个仿真步骤,即热源沿磨削方向Z轴上移动80步。很多学者对磨削热源分布模型进行了大量研究,有矩形热源分布模型、梯形热源分布模型和三角形热源分布模型,在平面磨削中,目前被大多数学者接受的是三角形热源模型,如图3所示。

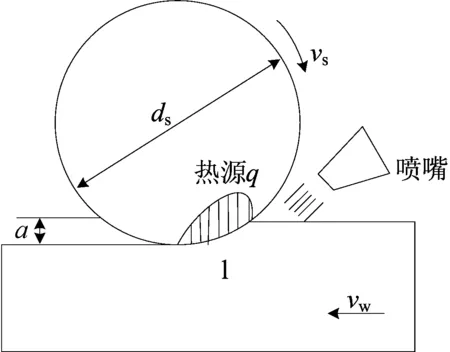
图3　三角形热源分布模型

本实验的三角形移动热源模型如图4所示,即在Abaqus中通过对工件磨削表面2列单元网格分别加载0.33q和q的热量来近似三角形热源模型,并使热源沿磨削方向移动。

磨削热来源于磨削功率的消耗。磨削加工时,磨除单位体积(或质量)金属所消耗的总能量为qt,单位为J/mm3,可表示为[11-12]:

(7)

其中,vs为砂轮磨削表面线速度;vw为工件移动速度;vt为砂轮与工件间的相对速度;a为磨削进刀深度;Ft为切向磨削力；lc为磨削接触长度。

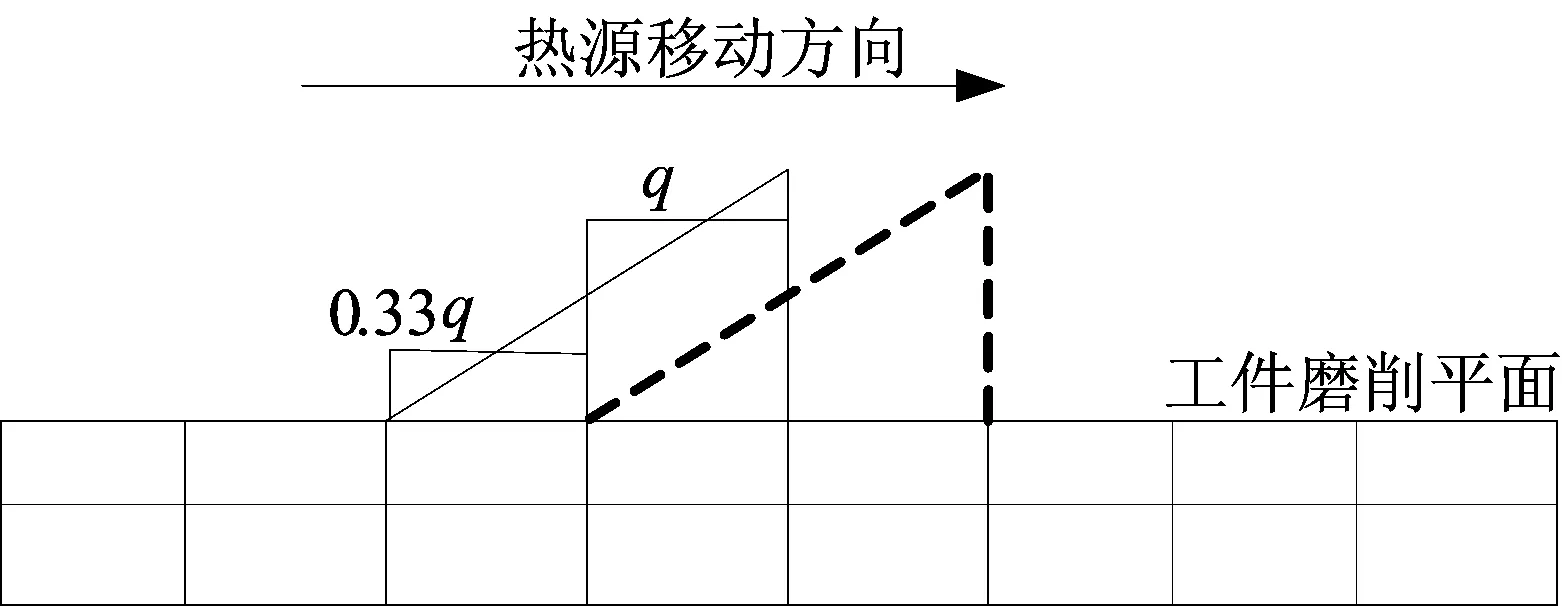
图4　热源移动模型

在实际磨削过程中,磨削总能量qt不会全部进入工件,还有大量能量进入砂轮和冷却液,而进入工件的热量和总能量比值称为能量比例(ε),计算公式如下:

(8)

变换可以得到进入工件的热量值q为:

(9)

一般来说,在一组实验条件下,磨削过程中能量比例ε变化不大,只和砂轮性能、磨削参数等有关,根据文献[12]的研究,将ε取为13%。

2.3磨削接触长度计算

在磨削过程中,准确计算磨削接触长度是磨削热分析精度重要因素之一。根据定义,几何磨削接触弧面是在一定的磨削深度下,砂轮的理想外圆表面与工件在磨削区内重合部分的曲面;几何磨削接触面积为接触长度乘以接触宽度,动态磨削面积则和砂轮表面形貌、磨削工艺参数、砂轮和工件的接触状态等因素有关,是个动态变化量。

在实际磨削情况中由于磨削过程十分复杂,砂轮、工件、磨粒等会发生弹性塑性变形,不同的磨削参数弹性变形大小不同,还有磨削热的影响,因此实际磨削接触长度计算十分复杂,一般用几何磨削接触长度来代替实际磨削接触长度。

对于齿轮的成形磨削3面相接触,其接触面为齿槽部分的3个面,因此在计算磨削体积时,其接触长度lc应该为一个齿的齿面及齿槽部分的长度和,如图5所示,面1和面2可以看做齿轮磨削接触面。由于是圆柱齿轮,根据对称性,计算其中一面即可。面1由2部分组成：渐开线部分AC段和基圆与齿根圆之间的过渡曲线AD段。

根据图5中齿轮的渐开线形状,可以得到AB段长度，即

(10)

其中，lAE=0.5θarb，θa=invαa,αa=arccos(rb/ra);lEB=παarb/90。因此可以得到:

(11)

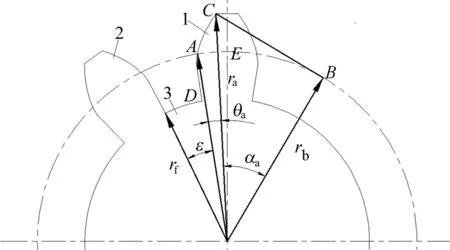
图5　磨削接触长度示意图

根据磨削接触长度定义,可以计算出整个齿轮成形磨削接触长度lc为:

(12)

根据磨削相关热理论,可以将磨削接触长度计算公式代入(9)式,计算出齿轮磨削过程中表面加载热量值q。

3成形磨齿温度场有限元仿真

齿轮材料为40号合金钢，基本参数见表1所列。

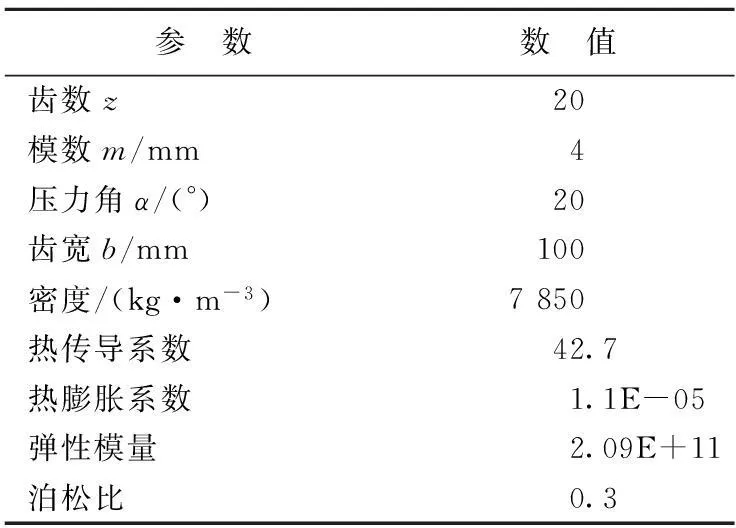
表1　齿轮的基本参数

在进行温度场有限元仿真时,根据有限元分析模型,按照表1齿轮基本参数设置齿轮的参数和材料属性,选择分析类型为瞬态。根据实际加工情况,定义好有限元仿真初始条件、边界条件、热约束和热载荷大小,确定载荷步。由移动的矩形线热源的载荷总长和vw,得热源q的加载时间τ=0.037 s,每个载荷步时间取为0.003 7 s,将热源载荷施加在三维模型的节点上进行磨齿温度场仿真分析。

经过求解,绘出的加载载荷步过程中磨齿温度场云图如图6所示,温度值范围约为69.17～143.2 ℃。从图6可以看出在进行齿轮的三面接触成形磨削过程中,当砂轮磨削到金属的某一位置时,该处齿槽和两侧的齿顶部分温度分布较高,其余部分的热量分布较少、温度低。其中主要原因是齿槽部分由于2面齿面和砂轮加工时形成封闭的空间,热量不易传输出去,导致热量集中于齿槽部分。选取左、右齿廓上的节点,绘制的节点温度变化曲线如图7所示。

图6　砂轮磨削过程中的温度云图

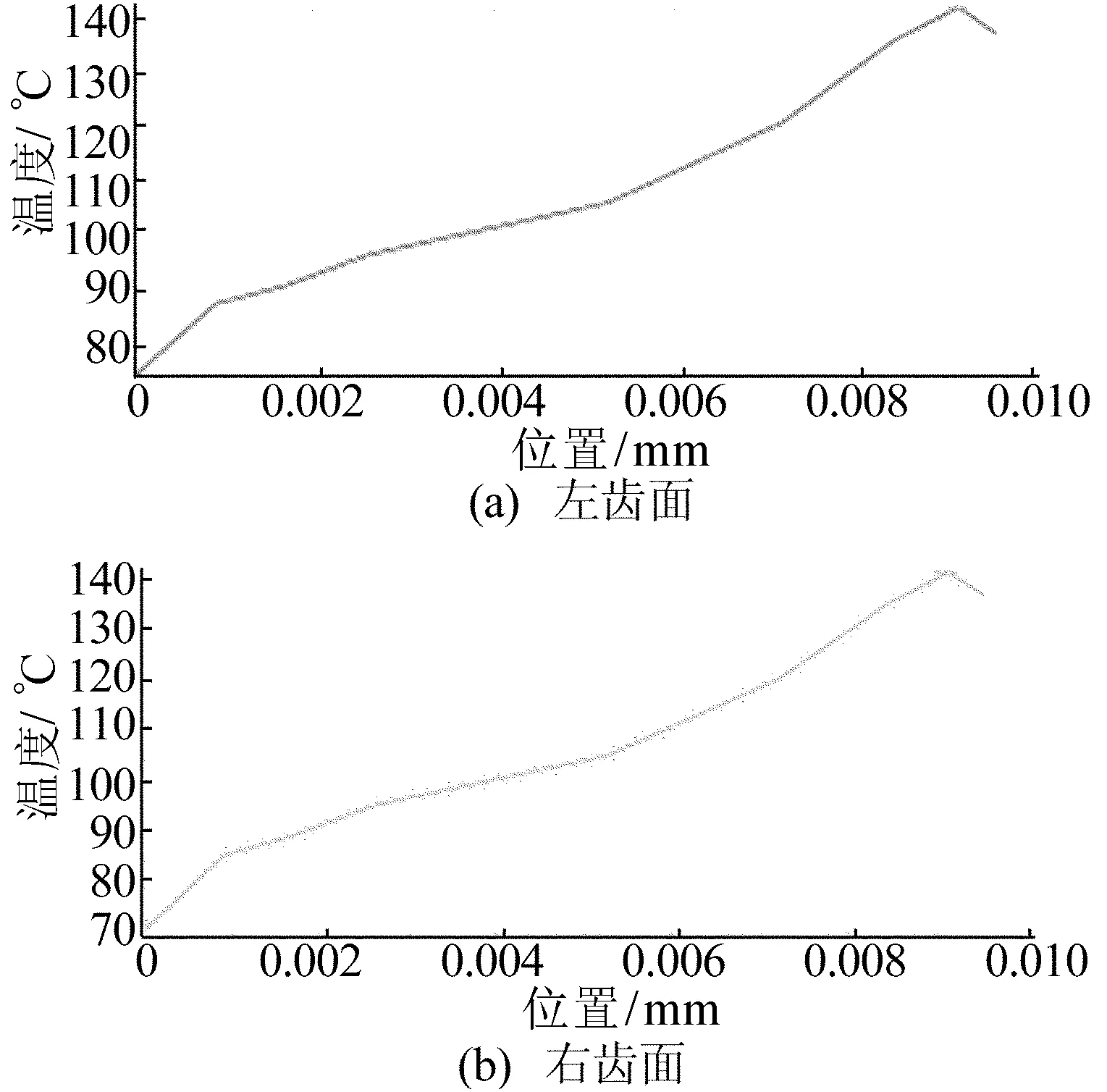
图7　齿轮齿面轮廓路径上的节点温度曲线

图7显示左、右两齿面齿顶部分热量集中,主要因为齿轮材料钢的传热能力比空气传导大,整个齿面上的热量往齿顶扩散；同时由于是圆柱直齿轮,左、右两齿面的热量走势也是一样的。

4成形磨齿热力耦合有限元仿真

齿轮的成形磨削过程中,随着砂轮的高速磨削,剧烈的摩擦和切削使得局部区域的温度迅速上升,可能会引起磨削表面金相组织变化,使磨削表面残余应力变大,从而影响齿轮磨削表面质量和精度。为了分析这种高温、高应变率耦合的大变形问题,本文采用热-力耦合的动态显式积分有限元方法进行齿轮成形磨削热-力耦合分析。

热-力耦合分析方法有2种方式:① 顺序耦合法，首先进行热分析,然后将求得的节点温度作为体载荷施加到结构应力分析中,这种方法只考虑温度对变形的影响,不考虑变形对温度的影响;② 直接耦合法，使用具有温度和位移自由度的耦合单元,同时得到热分析和力分析的结果,这种方式得到的结果是热-力全耦合的。当温度场和应力场相互作用非线性程度不高时,使用顺序耦合法更加有效,直接耦合法不适于步骤多的分析。根据齿轮成形磨削的特点,本文采用顺序耦合法更为合适。

在Abaqus中经过顺序热-力耦合分析,得到的仿真结果如图8～图10所示。

由图8可知,在磨削过程中,应力较大的部位集中在剩余工件的表层,远离磨削处的应力较小;当砂轮磨削到金属的某一位置时,该处的应力最大,而当砂轮离开时,该处的应力开始减小;最大磨削热应力产生于齿轮被磨削接触区域中心,包括齿根部分中心、两侧齿面中心部分,最大热应力可以达到7.17×106N。

图8　齿轮成形磨削热应力云图

图9是砂轮磨削过程中齿轮沿着X、Y方向上的热变形云图,从图中可以看出X方向上热变形最大值为4.60×10-7m,Y方向上热变形最大值为4.62×10-7m,这对于齿轮成形磨削精度具有重要影响。图10是齿轮磨削局部应变云图放大200倍后的结果,可以很清楚地看出，轮齿被磨削面产生比较大的热变形,增大了齿厚。

图9　砂轮磨削过程中的变形云图

图10　放大200倍后的变形云图

5结束语

通过齿轮成形磨削温度场和热-力耦合仿真分析可知,当砂轮磨削到金属的某一位置时,位于磨削弧的齿槽和齿顶处的磨削瞬态温度最高,因而磨削弧中心附近的瞬态磨削热应力与变形最大,直接影响磨削残余应力;磨削瞬时高温将使磨削表层软化,影响磨削层硬化程度和金相组织变化,这些都对齿轮磨削表面性能产生重要影响,其中磨削瞬时高温的影响是关键。在加工过程中应特别注意磨削参数的选择,这将对齿轮的磨削质量产生很大的影响。

本文为齿轮成形磨削提供了一种磨削热-力耦合分析的方法,对提高齿轮成形磨削质量和精度具有一定的实际意义。

[参考文献]

[1]Ren X Z, Du X Y, Su J X, et al. Error analysis and simulation of gear form grinding[J]. Advanced Materials Research, 2011, 189/190/191/192/193: 3109-3112.

[2]袁鸿,张金,黄筱调.成形磨齿齿形误差分析[J]. 机械科学与技术, 2012, 30(12): 2141-2145.

[3]韩江,杨清艳,张魁榜,等. 数控成形砂轮磨齿机床几何误差建模与补偿[J].合肥工业大学学报:自然科学版,2012,35(12):1585-1588，1609.

[4]Malkin S.Grinding technology:theory and applications of machining with abrasives[M].New York:Wiley,1996：96-112.

[5]周志雄,毛聪,周德旺,等.平面磨削温度及其对表面质量影响的实验研究[J].中国机械工程,2008,19(8):980-984.

[6]Zuo D W,Matsuo T.Significance of grinding temperature in metal removal[J].Key Engineering Materials,2001,202/203(6):57-60.

[7]Jaeger J C.Moving sources of heat and the temperature at sliding contacts[J].Proceedings of the Royal Society of New South Wales,1942,76:203-224.

[8]Outwater J O, Shaw M C. Surface temperatures in grinding[J].Transactions of the ASME, 1952, 74: 73-86.

[9]Hahn R S. The relation between grinding conditions and thermal damage in the workpiece[J].Transactions of the ASME,1956,78:807-812.

[10]贝季瑶.磨削温度的分析与研究[J]. 上海交通大学学报,1964, 28(3):45-49.

[11]Kohli S P,Guo C,Malkin S, et al. Energy partition to the workpiece for grinding with aluminum oxide and CBN abrasive wheels[J].Journal of Manufacturing Science and Engineering, 1995, 117(2):160-168.

[12]张魁榜,韩江,张丽慧,等.基于传热反算建立磨削三维热模型的新方法[J]. 中国机械工程, 2013, 24(18): 2480-2484.

(责任编辑胡亚敏)