多无人机编队协同目标分配的两阶段求解方法

叶青松， 胡笑旋， 马华伟

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.合肥工业大学 飞行器网络系统研究所，安徽 合肥 230009）

无人机（UAV）有隐蔽性好，起降简单，操作灵活等特点，可以代替人去完成枯燥、恶劣、危险的任务，在军事和民用领域发挥着重要的作用。任务分配是指在多任务和多无人机之间进行合理规划，充分考虑任务约束、无人机性能约束和环境约束，对无人机进行任务指派，使它们能够以最佳的方式完成既定任务［1－2］。

任务分配是一类组合优化问题，其解空间随着无人机数量和任务数量的增加而呈指数级增加，从而给求解带来极大的困难。对于不同场景下的任务分配，人们提出了多种任务分配模型，常见的模型有网络流模型（Network Flow Model，NFM）［3－5］、混合整数线性规划模型（Mixed Integer Linear Programming，MILP）［6－9］和车辆路径问题模型（Vehicle Routing Problem，VRP）［10］等。这些模型有着多种求解算法，包括满意决策算法［11－12］、合同网算法［13－14］、粒子群算法［15－16］、遗传算法［17］、蚁群算法［18］等。文献［8］提出了以任务最小完成时间为目标的多UAV任务分配和航迹规划的混合整数规划模型，以及任务重分配的思路；文献［9］建立了多UCAV协同任务分配的形式化模型，并使用基于进化计算的算法求解；文献［13］在建立初始分配的基础上，引入负载系数参数，使用合同网算法实现对任务的分配；文献［17］提出了任务分配问题的遗传算法求解思路，在建立模型时，考虑了无人机对目标的毁伤概率、目标的价值以及航程；文献［18］考虑了动态任务的时间约束和无人机的能力差别，建立了扩展的协同多任务分配模型，并使用基于分工的蚁群算法对模型加以求解。

目前，大多数文献研究的是在特定的任务分配场景中，利用现有或者改进的算法对建立的模型进行求解，这些研究工作能够获得较好的任务分配结果。但是，考虑到战场环境对算法运行时间的严格约束，目前的很多方法在执行速度上仍然不能满足要求。如蚁群算法等启发式算法的求解过程在一个控制中心上执行，是一种集中式计算，在任务分配规模较大时，运行速度较慢；合同网算法采取投标竞标的方式进行决策，无人机之间相互发送投标竞标数据包，是一种分布式的计算方法，但是该方法依赖于无人机之间的通信，在任务分配规模较大时容易形成通信阻塞。

本文针对多无人机编队对地面目标打击任务的分配问题，提出一种两阶段的求解方法，首先进行编队级目标分配（后文提到的任务分配等同于目标分配），对目标聚类形成目标簇，确定每个无人机编队所攻击的目标簇，然后进行编队内目标分配，将每一个目标分配给具体无人机，多个编队的编队内目标分配可以并行执行。编队级任务分配是集中式计算，可在控制中心上执行；编队内任务分配是分布式计算，可在编队内的长机上执行。两阶段求解方法降低了任务分配问题的求解规模，达到提高求解效率的目的。

1 问题描述

面对复杂的战场环境，多机协同能提高任务的完成质量和效率，这使得多机协同任务分配的研究具有实际意义。

本文研究的是多无人机编队对多目标打击任务的分配问题，若干个无人机编队从不同的机场出发，打击一定数量的地面目标，完成任务后返回机场。每个无人机编队中有若干架无人机，其中一架长机，其余的为僚机。目标的位置已知，每个目标只能被一架无人机攻击，无人机攻击的总目标数量不得多于其载弹数。目标分配的准则是整体攻击收益的最大化。

本文所用符号如下：令U＝｛Um｜1≤m≤M｝表示M个无人机编队，无人机编队Um位于第m个机场Am，机场Am的位置记为（ax，ay）；无人mm机编队Um中有｜Um｜架无人机，记为Um＝，其中表示Um中的第r架无人机，无人机携带导弹数记为，导弹单位成本记为，航程单位成本记为。令T＝｛tq｜1≤q≤NT｝表示NT个地面目标的集合，目标tq的位置记为（tx，ty），价值记为vq。qq

2 问题分解

由于战场的高动态性，无人机目标分配需要在极短的时间内完成。因此，本文采用两阶段的方法对任务分配问题进行求解，将问题划分成编队级目标分配和编队内目标分配2个阶段。

（1）编队级目标分配。输入无人机编队数据以及目标数据，计算目标簇中心点，为无人机编队分配最近的目标簇，多次迭代直到中心点不再变化，输出每个无人机编队所分配的目标簇。

（2）编队内目标分配。每个无人机编队内的长机接受阶段1所分配的目标簇，并负责将目标簇中的目标分配给本编队内无人机，输出本编队内每个无人机攻击目标的路径。

在编队内目标分配过程中，每个编队的目标分配是并行执行的，同时，每个无人机在选择攻击目标时，是在其所属编队应打击的目标簇中选择，而不是在所有目标中选择。与直接进行目标分配相比，两阶段方法缩小了原始问题的规模，从而能够提高求解速度，缩短求解时间。

2.1 编队级目标分配

编队级目标分配的目标是形成M个目标簇，记为T＝｛T1，T2，…，Tn，…，TM｝，1≤n≤M，｜Tn｜表示目标簇Tn中的目标数目，目标簇Tn的中心点为Cn，每个目标簇分配给最近的无人机编队，每个无人机编队所分配的目标簇中的目标数目不得大于本编队载弹数。选取布尔型变量Xmn，Xmn＝1表示将目标簇Tn分配给无人机编队Um，其余Xmn＝0。d（Am，Cn）表示机场Am到目标簇Cn中心点的欧式距离（后文提到的距离指的是欧氏距离）。

编队级目标分配的模型如下：

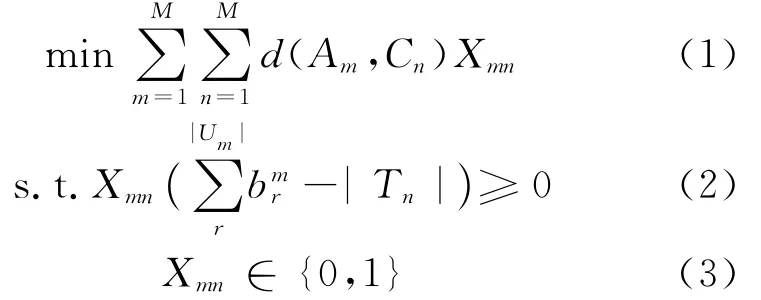
（1）式表示以无人机编队到目标簇中心的攻击距离和最小为目标，（2）式表示无人机编队所攻击的目标簇中目标数不得大于本编队载弹数。

本文使用改进的K－Medoids［19］算法求解编队级目标分配。K－Medoids是一种基于划分的聚类算法，其核心思想是将已知的若干个数据对象划分成多个簇，每个簇中的对象离本簇中心较近，而离其他簇中心较远。

K－Medoids是一种改进的K－means［20］算法，两者的区别在于：K－Medoids算法在计算簇中心时，选取的是本簇中的一个数据对象，而不是本簇中所有数据对象的属性均值，因而，K－Medoids算法不易受孤立数据对象影响算法，产生簇中心大幅度偏移，具有较强的鲁棒性和准确性［21－22］。

基于K－Medoids算法的编队级目标分配过程如下：

（1）随机选择M个目标作为M个目标簇的初始中心点。

（2）将无人机编队分配到最近的目标簇中心点，每个中心点对应一个无人机编队。

（3）循环迭代每个目标，将每个目标聚类到最近的目标簇中心点，若出现目标簇内目标数大于本目标簇分配给的无人机编队载弹数，从本目标簇中选取一个到其他目标簇中心点最近的一个目标，将该目标转移到最近的中心点对应的目标簇中。规定一次目标迭代中，2个目标簇之间不得相互转移目标，从而保证不出现回路。

（4）更新目标簇中心点，在每个目标簇中，选择到本目标簇中其他目标距离和最小的目标作为该目标簇新的中心点。

（5）当目标簇中心点不再变化时，结束，并输出目标簇，否则转步骤（2）。

通过编队级目标分配，每个无人机编队分配了最近的目标簇，同时，无人机编队攻击的目标簇中的目标数目不超过编队的导弹载荷，使得无人机编队攻击任务负载均衡。

编队级目标分配为编队内目标分配提供输入，无人机编队间可以并行执行目标分配，从而，降低了每个无人机编队目标分配复杂度，从整体上提高了目标分配求解效率。

2.2 编队内目标分配

假设无人机编队Um攻击目标簇Tn，每个无人机可以攻击多个目标，每个目标只能被无人机攻击1次。将无人机编队Um所在机场Am节点编号设为0，目标节点的编号取目标编号，形成节点集合H，i、j为H中2个节点。dij为节点i与节点j之间的距离。定义布尔型决策变量xrij，r表示无人机编队Um中的第r架无人机，则有：

编队内目标分配模型如下：

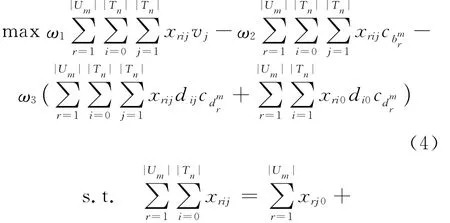
（4）式表示模型以无人机攻击目标带来的收益与航程成本之差最大化为目标；（5）式表示每个目标最多能被无人机攻击1次；（6）式表示每个无人机从机场出发并最终回到机场；（7）式表示无人机不能攻击超过其载弹数的目标。

本文选取蚁群算法求解编队内目标分配问题。蚁 群 算 法 （Ant Colony Optimization，ACO）［23］由意大利学者 Macro Dorigo受自然界蚂蚁觅食的行为启发而提出，该算法后多被应用于组合优化问题求解中。蚁群算法中的信息素更新机制使得蚂蚁朝着更优的路径聚集，与随机搜索算法相比，计算效率更高［24］。

本文使用蚁群算法求解编队内目标分配过程如下：

（1）设置蚂蚁数目为A，并对每只蚂蚁初始化，对目标节点间的信息素初始化。

（2）每只蚂蚁选择目标，并生成路径。

（3）每只蚂蚁进行信息素局部更新。

（4）更新最优路径。

（5）信息素全局更新。

（6）如果达到设定的最大循环次数G，则退出，否则转步骤（2）。

在步骤（2）中，每只蚂蚁选择下一节点的概率计算公式为：

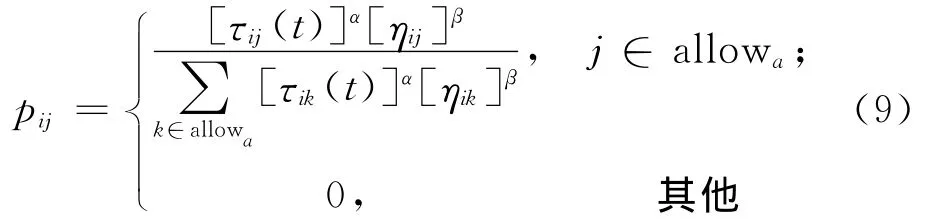
其中，τij（t）为t时刻节点i与节点j之间的信息素浓度；α为信息启发式因子；β为期望启发式因子；allowa为下一时刻蚂蚁a所能选择的节点；ηij为启发函数，其值为：

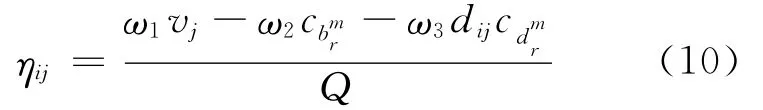
其中，Q为设定的信息素浓度归一值。

在步骤（3）中，信息素局部更新公式为：

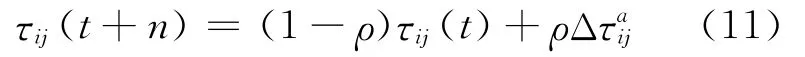
其中，τij（t＋n）为t＋n时刻节点i与节点j之间的信息素浓度；ρ为信息素局部更新控制参数；Δ的值为：

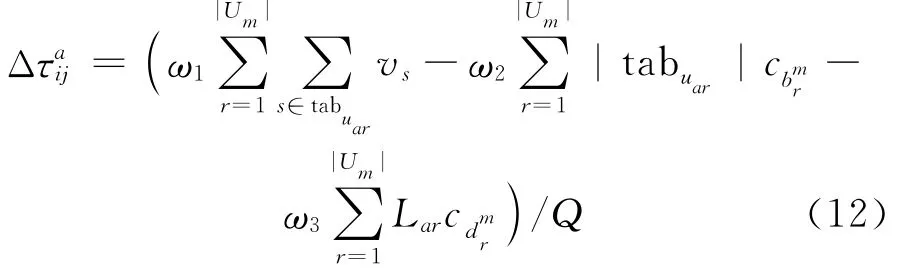
其中，tabuar为蚂蚁a代表无人机走过的路径；｜tabuar｜为该路径中的目标数目；Lar为tabuar的路径长度。

在步骤（5）中，信息素全局更新公式为：

其中，σ为信息素全局更新控制参数；Δτij的值为：

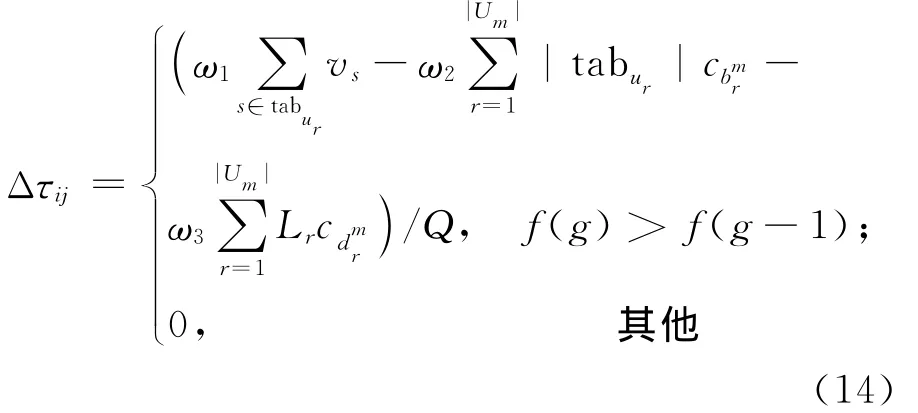
其中，f（g）为第g次迭代全局最优路径｛tabu，1…，tabu｝对应的目标函数值；Lr为无人机｜Um｜走过的路径tabur的长度。

3 仿真实验

仿真实验分为2个部分，首先用一组实验验证本文所提出的两阶段方法的可行性，然后进行多组不同编队数量、不同目标数量的目标分配对比实验，将本文方法和单阶段方法进行对比，验证本文方法的有效性。所谓单阶段方法，指的是不进行编队级目标分配，直接使用编队内目标分配算法对所有目标进行直接分配的方法。

本文选取100×100的二维场景，在场景内，随机生成了25个目标，并随机生成4个机场，部分数据见表1、表2所列。

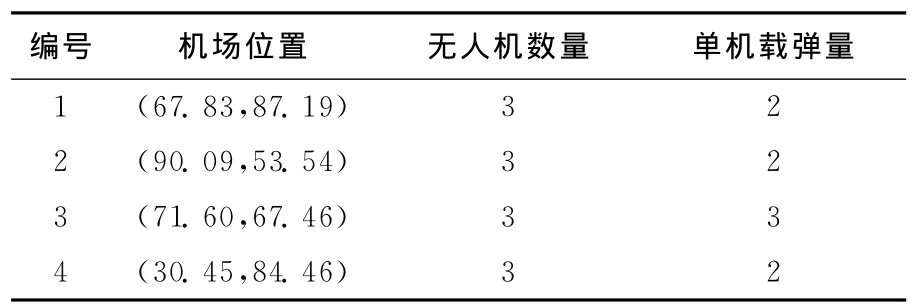
表1 无人机数据

表2 本文算法参数

实验在Intel Core2Duo E7500CPU，2GB RAM的实验机器上进行，算法执行时间为：编队级目标分配耗时0.04s，编队内目标分配耗时0.09s。运行结果如图1、图2所示。

图1中，无人机编队指向的目标表示该编队所要攻击的目标聚簇的中心，如无人机编队4所要攻击的目标聚簇中心点为目标5；图2显示了无人机编队中的每个无人机的攻击顺序。

接下来，本文分别选取了25、50、100、150、200个目标，3、4个编队，分别组合进行实验，记录两阶段方法和单阶段方法的运行结果和运行时间，如图3、图4所示。

由图3可以看出，两阶段方法的执行时间明显低于单阶段方法，在目标数量较多时，两阶段方法能大幅度降低目标分配问题的求解时间。从图4可以看出，在目标数为25、50、100、150时，两阶段方法求得的目标函数值略大于单阶段方法，只有在目标数为200时，两阶段方法求得的目标函数值才小于单阶段方法。因此，使用两阶段方法求解目标分配问题不会明显降低解的质量。

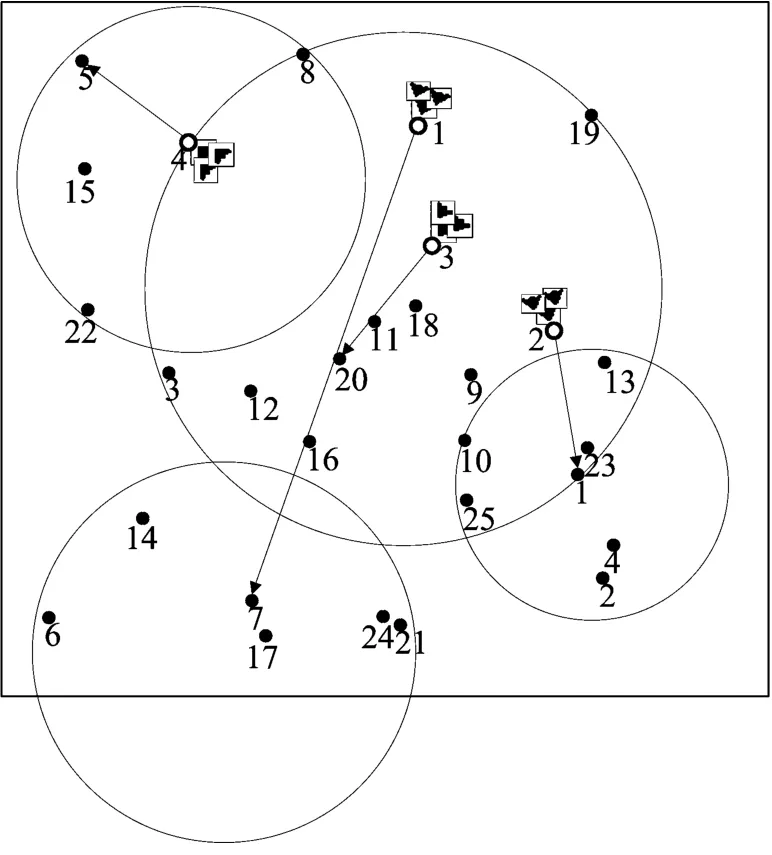
图1 编队级目标分配

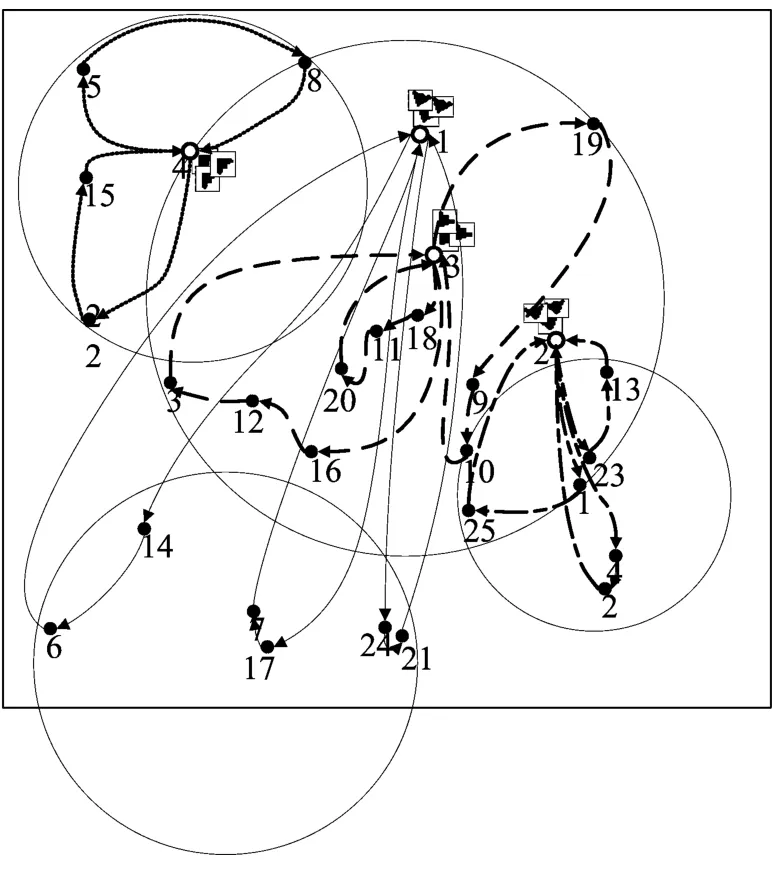
图2 编队内目标分配

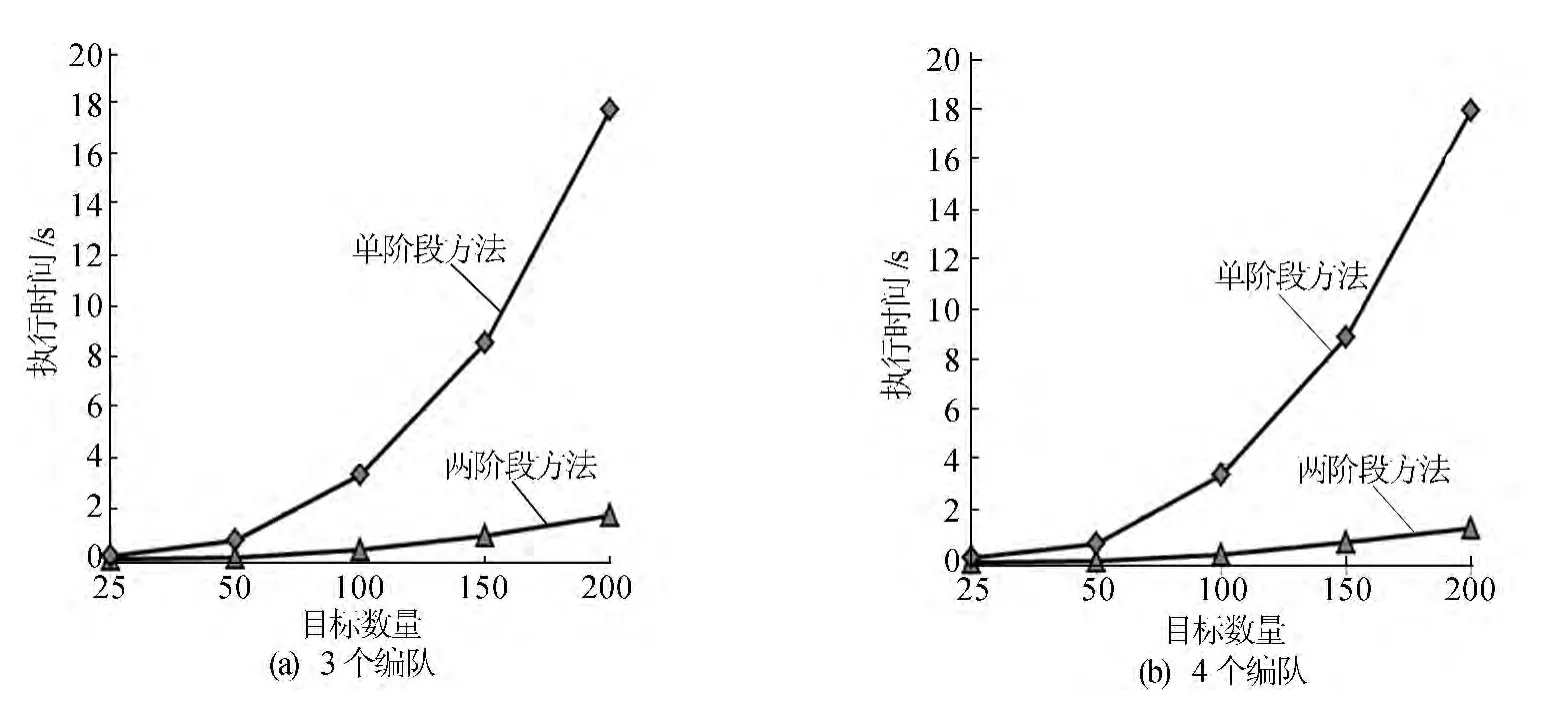
图3 2种方法执行时间对比图

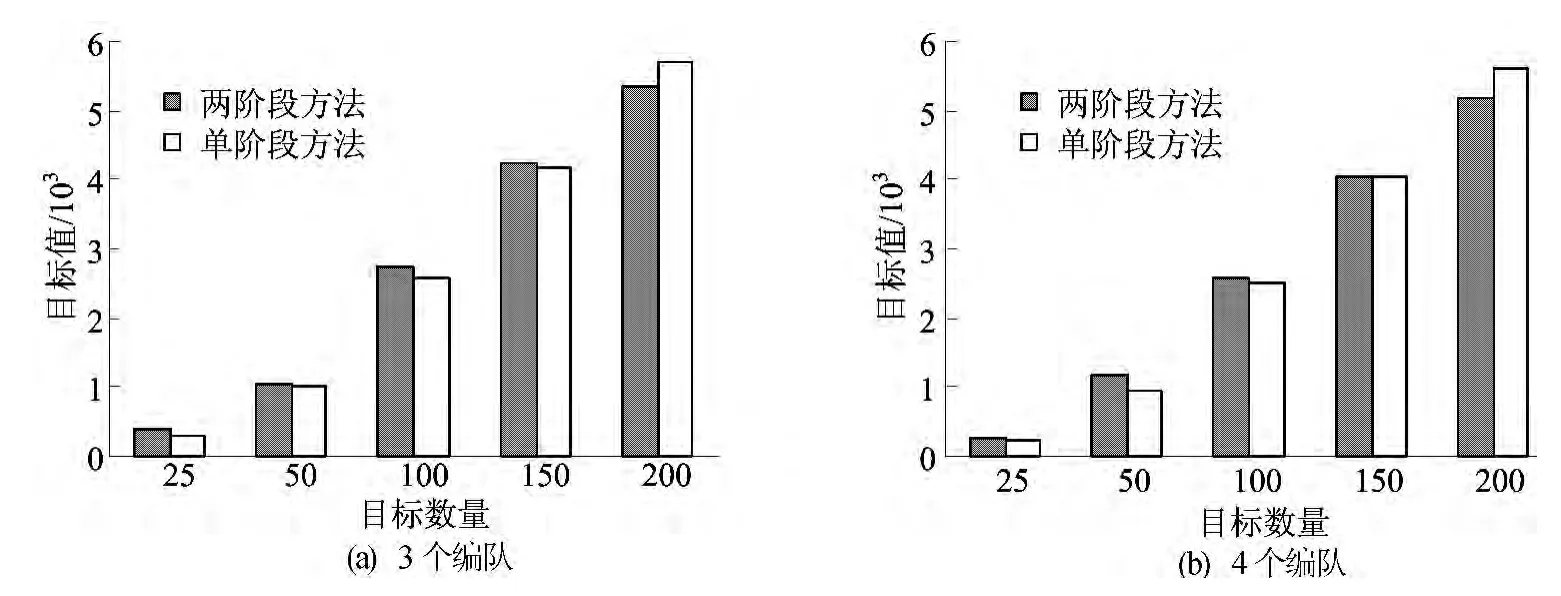
图4 2种方法目标值对比图

4 结束语

本文提出了一种新的两阶段方法来求解多无人机编队协同目标分配问题，将问题分解成编队级目标分配和编队内目标分配2个阶段，首先将目标聚成若干个目标簇，将目标簇分配给不同的无人机编队，然后，每个编队的长机将所分配到的目标簇中的目标分配给编队内的无人机。本文给出了整个过程中的求解模型和算法，实验结果表明，该方法是可行和有效的。

该方法的目的是在一个合理的时间内生成一个令人满意的解决方案，而不是在一个不可接受的时间内找到全局最优解。该方法可以满足战场场景下对目标分配算法严格的运行时间要求，可以在实际应用中使用。此外，该方法是可扩展的，可以被应用到其他类型的智能体中。

［1］ 沈林成，陈 璟，王 楠.飞行器任务规划技术综述［J］.航空学报，2014，35（3）：593－606.

［2］ 唐苏妍，朱一凡，李 群，等.多Agent系统任务分配方法综述［J］.系统工程与电子技术，2010（10）：2155－2161.

［3］ Nygard K E，Chandler P R，Pachter M.Dynamic network flow optimization models for air vehicle resource allocation［C］／／American Control Conference，2001，Proceedings of the 2001，Vol 3.IEEE，2001：1853－1858.

［4］ Schumacher C，Chandler P，Pachter M，et al.UAV task assignment with timing constraints［C］／／AIAA Guidance，Navigation，and Control Conference and Exhibit，Austin，Texas，2003.doi：10.2514／6.2003－5664.

［5］ Schumacher C，Chandler P R，Rasmussen S J，et al.Task allocation for wide area search munitions with variable path length［C］／／American Control Conference，2003，Proceedings of the 2003，Vol 4.IEEE，2003：3472－3477.

［6］ Alighanbari M.Task assignment algorithms for teams of UAVs in dynamic environments［D］.Massachusetts Institute of Technology，2004.

［7］ Griggs B J，Parnell G S，Lehmkuhl L J.An air mission planning algorithm using decision analysis and mixed integer programming［J］.Operations Research，1997，45（5）：662－676.

［8］ Bellingham J，Tillerson M，Richards A，et al.Multi－task allocation and path planning for cooperating UAVs［M］.Cooperative Control：Models，Applications and Algorithms.Springer US，2003：23－41.

［9］ 叶媛媛，闵春平，朱华勇，等.基于整数规划的多 UCAV任务分配问题研究［J］.信息与控制，2006，34（5）：548－552.

［10］ O’Rourke K P，Carlton W B，Bailey T G，et al.Dynamic routing of unmanned aerial vehicles using reactive tabu search［J］.Military Operations Research，2001，6（1）：5－30.

［11］ 廖 沫，陈宗基.基于满意决策的多机协同目标分配算法［J］.北京航空航天大学学报，2007，33（1）：81－85.

［12］ 叶媛媛，闵春平，沈林成，等.基于满意决策的多 UAV协同目标分配方法［J］.国防科技大学学报，2005，27（4）：116－120.

［13］ 钱艳平，夏 洁，刘天宇.基于合同网的无人机协同目标分配方法［J］.系统仿真学报，2011，23（8）：1672－1676.

［14］ 刘 波，张选平，王 瑞，等.基于组合拍卖的协同多目标攻 击 空 战 决 策 算 法 ［J］.航 空 学 报，2010，31（7）：1433－1444.

［15］ 李 炜，张 伟.基于粒子群算法的多无人机任务分配方法［J］.控制与决策，2010，25（9）：1359－1363.

［16］ 杜继永，张凤鸣，杨 骥，等.多UCAV协同任务分配模型及粒 子 群 算 法 求 解 ［J］.控 制 与 决 策，2012，27（11）：1751－1755.

［17］ Chen G，Cruz J B，Jr.Genetic algorithm for task allocation in UAV cooperative control［C］／／AIAA Guidance，Navigation，and Control Conference and Exhibit，Austin，Texas，2003.doi：10.2514／6.2003－5582.

［18］ 苏 菲，陈 岩，沈林成.基于蚁群算法的无人机协同多任务分配［J］.航空学报，2008，29（Z1）：S184－S191.

［19］ Kaufman L，Rousseeuw P J.Finding groups in data：an introduction to cluster analysis［M］.John Wiley ＆ Sons，2009：108－110.

［20］ MacQueen J.Some methods for classification and analysis of multivariate observations［C］／／Proceedings of the fifth Berkeley Symposium on Mathematical Statistics and Probability，Vol 1.Berkeley，Calif：Univ of Calif Press，1967：281－297.

［21］ Park H，Lee J S，Jun C.A K－means－like Algorithm for K－medoids clustering and its performance［C］／／Proceedings of ICCIE，2006：102－117.

［22］ Park H S，Jun C H.A simple and fast algorithm for K－medoids clustering［J］.Expert Systems with Applications，2009，36（2）：3336－3341.

［23］ Dorigo M，Gambardella L M.Ant colony system：a cooperative learning approach to the traveling salesman problem［J］.IEEE Transactions on Evolutionary Computation，1997，1（1）：53－66.

［24］ 于 雷，任 波，鲁 艺.自适应蚁群算法的多机协同空战目标分配方法［J］.火力与指挥控制，2008（6）：49－51.