中国园林的分形同构现象解析

陈晶晶，郭二辉，郑晓军，田朝阳

(河南农业大学林学院，河南郑州 450002)

西方传统设计的数学基础是正方形、三角形、圆形等简单规则形构成的欧几里得几何学，欧氏几何被当作目前包括风景园林在内的几乎所有设计学科的几何基础［1］。欧氏几何形构图理论，与其说是对自然界复杂形态理性的简化、抽象，不如说是对自然界复杂性的否定，尤其是对大尺度的场地规划采用欧氏几何会对自然造成极大的破坏［2］。早在1889年，西方城市设计的先驱、奥地利建筑师卡米诺·西特［3］曾抨击规则形用于城市设计是对艺术的扼杀，因为自然是所有艺术形式的源泉。对于根本不含简单规则形的中国传统园林，如用欧氏几何的原理来解析，无异于用西方歌剧理论来诠释中国的京剧。

以师法自然为特征的中国传统园林有没有几何学基础作为科学的依据呢?王庭蕙等［4-5］利用拓扑几何学理论解读了中国传统园林中部分未知的几何规律，为我们开启了科学解读传统园林的榜样。1975年，美籍法国数学家曼德勃罗编写的《分形对象:形，机遇与维数》一书，使得人们对纷繁多样的自然界形态有了新的认识，标志着分形理论的诞生［6］，为师法自然的艺术设计提供了科学的几何学基础。

1 分形几何理论

1.1 分形的概念

在自然界中，存在着许多传统欧几里得几何学所不能描述的一大类复杂的、无规则的几何现象，例如，蜿蜒曲折的海岸线、起伏不定的山脉、粗糙不堪的断面、变幻无常的浮云、纵横交错的血管、令人眼花缭乱的满天繁星等等，它们的特点是极不规则或极不光滑的［6］，这就是分形几何体。分形几何学是一门以非规则几何形态为研究对象的几何学，由于不规则的现象在自然界中是普遍存在的，因此分形几何学又被称为大自然的几何学。

1.2 分形几何的基本特征

分形几何体具有自然形体的“不规则形”和“局部与局部、局部与整体的相似性”2大基本特征。

1.3 分形几何的应用

目前分形几何在建筑设计、城市规划、区域规划、园林植物等许多领域都有广泛的应用［7-11］。但是，在园林分析和设计中未见报道。

2 中国传统园林中的分形同构现象

2.1 中国园林设计理论与分形理论

分形几何理论的2大特征与中国传统园林有着某种意义的契合。第一，中国传统园林的设计手法是师法自然，即模拟自然要素的不规则形态。第二，中国传统园林“移山缩水” “拳山勺水”，是对自然要素的科学的地理重构［12］，即局部与整体的高度关联和有机结合。

2.2 中国园林复合形的不规则特性

中国园林的复合形 (图1)，指由直线、曲线和折线组成的不规则形［2］，是师法自然的产物，与自然界的分形几何体极为一致，都是不规则的几何形体。

图1 中国传统园林中的不规则复合形

2.3 中国园林复合形的自相似性

以古典园林谐趣园、退思园、狮子林、留园等众多名园为例。

图2-6可以看出，其各个园子的场地边界、建筑群体边界、水边界、路径的边界存在自相似性，即分形同构现象。

图2 谐趣园边界、建筑群体布局内外边界、路径边界、水系边界的分形同构

图3 退思园边界、建筑群体布局内外边界、路径、水系的分形同构

图4 网师园边界、建筑群体布局内外边界、路径、水系的分形同构

各个园子的各类要素形态，通过取形、微调、缩放、旋转，达到与园址形态的分形相似。而园址的形态，是取形的基础。各种园林要素的边界形态，与园址的边界形态具有极大的相似性，它们之间也存在相似性。

2.4 基于分形理论的中国园林构架

图7为通过取形和缩放2种方法模拟的谐趣园建筑群体布局、路径、水系边界的分形图，如果对

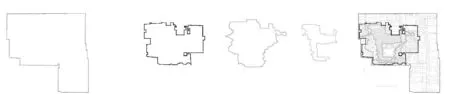
图5 狮子林边界、建筑群体布局边界、路径、水系的分形同构

图6 留园中部边界、建筑群体布局边界、路径、水系的分形同构

图7 模拟谐趣园建筑群体布局边界、路径、水系的分形同构各要素的形态进一步微调 (理微)、旋转 (互锁、互含、向心)，便可得到类似谐趣园的真实场景。

3 中国现代园林中的分形同构现象

中国传统园林的现代化面临诸多问题，最突出的问题是时代变迁下的尺度推移问题，即古典江南小尺度下的园林，如何在科学设计方法的指导下，适应大尺度公园、风景名胜区、各类城市绿地的设计。

分形几何的“不规则形”和“局部与整体的相似性”2大基本原则，也许为解决这一问题提供了思路和方法。实际上，历史上的大尺度皇家园林圆明园、颐和园、避暑山庄已经在无意识地使用分形几何方法，实现了尺度的推移;中国现代大尺度园林中的佳作花港观鱼和方塔园、太子湾公园、紫竹院公园、陶然亭公园 (图8-11)中也出现了大量不规则的分形几何构形，其山、水、地形、边界以及建筑布局都是运用分形几何理论的结果。

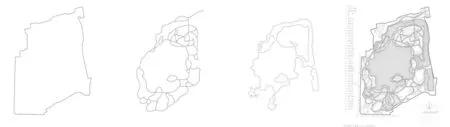
图8 上海长风公园边界、路径、水系的分形同构

图9 杭州花港观鱼公园的边界、路径、水系的分形同构

图10 杭州太子湾公园的边界、路径、水系、建筑群体布局的分形同构

图11 西安四盒园的边界、路径、园墙、建筑群体布局的分形同构

4 小结

西方园林界对自然的美学认可，始于17世纪;西方数学界对自然的科学认可，则迟至1975年分形几何学创立时。中国传统园林中对自然美的认知和对分形理论的无意识运用长达千年。如果说拓扑几何中的太极图是中国人世界观、宇宙观的图示表达，那么，中国传统园林中的分形意识是中国人自然观的展示。中国园林的核心设计哲学依然是“尊重自然，师法自然”。相对于“机械”的欧氏几何，“有机”的分形几何理论和方法不仅可以承载这种设计哲学，而且有助于我们建立中国传统园林的高级图形语汇，构成理论并用于现代风景园林实践。

［1］ 郭湧.当下设计研究的方法论概述［J］.风景园林，2011(2):68-71.

［2］ 田朝阳，闫一冰，卫红.基于线、形分析的中外园林空间解读 ［J］.中国园林，2015，31(1):94-100.

［3］ 卡米诺·西特.城市建设艺术［M］.仲德崑，译.南京:东南大学出版社，1990.

［4］ 朱光亚.中国古典园林的拓扑关系［J］.建筑学报，1988(8):33-36.

［5］ 王庭蕙.中国园林的拓扑空间 ［J］.建筑学报，1999(11):60-63.

［6］ 张济忠.分形［M］.北京:清华大学出版社，1995.

［7］ 叶俊，陈秉钊.分形理论在城市研究中的应用［J］.城市规划汇刊，2001(4):38-42.

［8］ 田达睿，周庆华.国内城市规划结合分形理论的研究综述及展望 ［J］.城市发展研究，2014，21(5):96-101.

［9］ 冒亚龙，雷春浓.一种理性的建筑设计与评价视角:应用分形的建筑设计尝试［J］.重庆建筑大学学报，2005，27(4):4-9.

［10］ 张霜霜.浅析论分形理论在建筑设计中的应用［J］.四川建筑，2014(5):56-58.

［11］ Jiang W，Ji C C，Zhu H.Fractal study on plant classification and identification ［J］.International Workshop on Chaos—Fractals Theories and Applications，2009:434-438.

［12］ 董莳.地理重构与情境剪辑: “空间地理”的意义构建［D］.杭州:中国美术学院，2011.