基于链路预测的全国活羊调运网络重构

樊洁茹，孙向东，戴 琪，靳 祯，4

（1．中北大学 理学院，山西 太原030051；2．动物卫生与流行病学中心，山东 青岛266114；3．阿尔山市农畜产品质量安全监督检测站，内蒙古 兴安盟137800；4．山西大学 复杂系统研究所，山西 太原030006）

0 引 言

小反刍兽疫俗称羊瘟，是由小反刍兽疫病毒引起的一种急性病毒性传染病，属我国规定的一类动物疫病．本病主要感染山羊、绵羊等小反刍动物，发病率高达100%，在严重暴发时，死亡率为100%．2014年春季，全国多个省份突然爆发小反刍兽疫疫情，且传播速度快，空间分布广，疫情呈现全国性扩散趋势，全国羊群高度易感．据初步调查，疫情传播以活羊的长途调运为主，了解活羊调运网络对研究小反刍兽疫的传播至关重要．然而大规模的流调需要耗费大量的人力、物力、财力，短时间内不可能实现．现实中只得到活羊调运的部分信息，因此，寻找真实的活羊调运网络，是我们迫切需要解决的问题．得到真实完整网络的方法之一就是链路预测［1－5］，其目的是网络重构［6－8］，即通过重新构建网络来恢复真实网络的面貌［9－10］．网 络 重 构 问 题 最 早 由Guimera 和Sales－Pardo提出，他们基于随机分块模型来进行网络重构［11］．此后，Zhang，Wang等人对随机分块模型及其可靠性进行了分析［12］．本文根据所获得的活羊调运部分信息，利用地理信息系统（ArcGIS软件）得到了全国活羊调运观测图，并利用链路预测的方法，重构了全国活羊调运网络．经过多次实验和市场调查，初步验证了所得结果的可靠性和真实性．根据本文所得到的重构网络，可预测每个节点的感染途径，感染时间和染病概率，从而有效地切断主要风险路径，将疫病控制在一个有限的范围内．

1 小反刍兽疫流行的观测网络

我国2007年首次在西藏自治区发现小反刍兽疫疫情，虽在2010年复发，但一直局限在西藏境内．2013年12月，该病疫情再次发生于新疆自治区，随后甘肃、内蒙古、宁夏等地先后发生疫情．经采取扑杀消毒、关闭市场、暂停调运等综合措施，疫情一度控制在西部四省份．

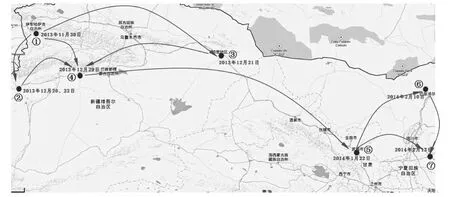
图1 2013年11月～2014年2月小反刍兽疫病例地理分布图Fig．1 Geogrophical distributing map of peste des petits rumihants from November 2013to February 2014

随着恢复西部省份活羊调运，加之内地处于春节后补栏高峰期，病毒通过欧亚大陆桥传入内地，并经活畜交易市场放大后流向全国多个省份．2014年3月份以来内地相继发生系列疫情，截止4月6日18时，全国已有18省份86地市144县区报告发生185起疑似或确诊疫情（见图2），对3月份以来的疑似和确诊疫情进行分析，超过90%的疫情是由活羊的长途调运引起的．因此了解动物的调运网络对进一步研究动物疫病的传播至关重要．

通过现场流行病学调查，结合市场链分析表明，我国活羊调运路线十分复杂，调运信息的采集相当困难，大规模的流调短时间内做不到，只能从局部去考虑．现实中采取疫情溯源及疫情跟踪方式，从小反刍兽疫疫情暴发点山东省嘉祥县入手，对所有引入疫点的活羊进行追溯性调查，以及对从疫点输出的活羊的去向进行跟踪调查，得到了2014年3月全国活羊调运部分信息．根据获得的不完全信息和数据，利用ArcGIS软件得到全国活羊调运网络观测图（见图3）．

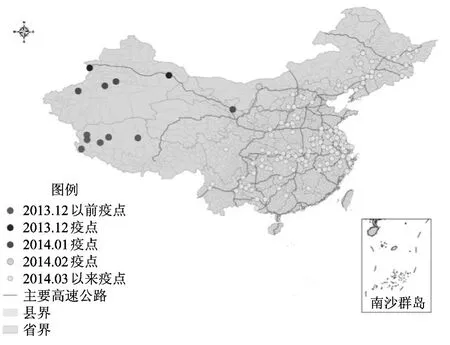
图2 2007年以来全国疫点分布图Fig．2 Distribution diagram about national epidemic spot since 2007

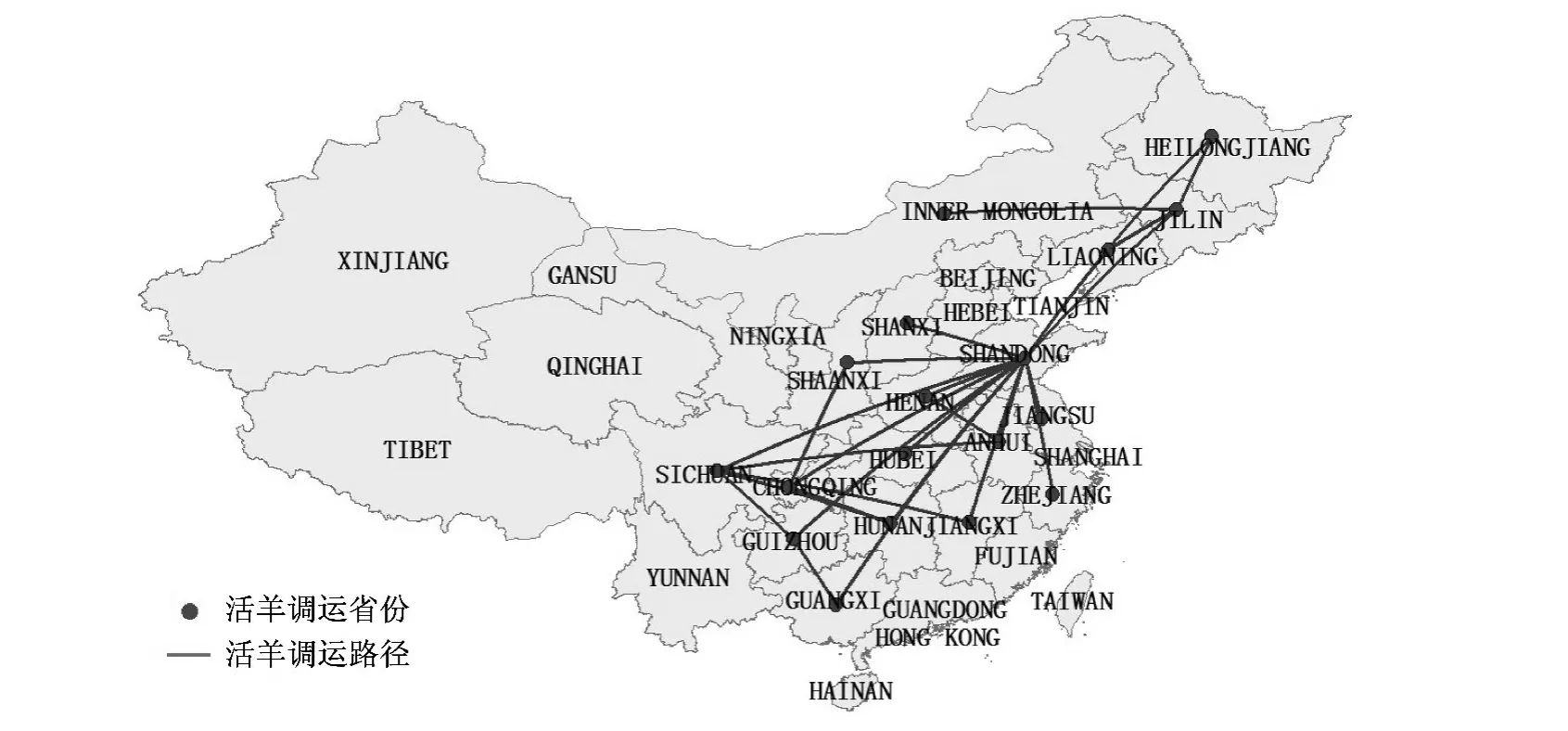
图3 全国活羊调运网络观测图Fig．3 Network observation map based on national live sheep migration

然而，根据疫情溯源及疫情跟踪所得到的调运数据是不完整的，存在调运情况的缺失．除此之外，一些被调查者鉴于某些原因会隐瞒或谎报调运事实，导致所得到的调运数据为虚假信息．因此观测网络中既有一些丢失边，又有一些虚假边，不能反映真实的活羊调运情况．如果采取实际调研的方法揭示观测网络中丢失与虚假的链路需要耗费高额的成本，所以本文将利用精确的链路预测算法［11］，得到更加接近于真实也更加完整的活羊调运网络．由两部分决定，一是网络被分成若干群的方案P3（见图4（a）），二是分属于两个群的两点之间产生连边的概率矩阵Q3（见图4（b））．网络中的节点被分为三组，分别由三种形状标识，概率矩阵Q 中的元素为式中：lOαβ为在AO中组α 和组β 之间的实际连边数，而rαβ为两组之间可能的最大连边数．

2 全国活羊调运网络的重构

链路预测的主要目的之一就是网络重构［13］．本文从以上不完整的活羊调运观测网络（图3）出发，利用随机分块模型预测网络中所有链路的信度，然后根据链路信度的排序识别丢失边和虚假边；通过改进后的贪婪算法，加入一些预测到的丢失边，删除观测网络中可能存在的虚假边，从而得到全国活羊调运重构网络．

2．1 随机分块模型

随机分块模型是最普适性的网络模型之一［14－17］．该模型将网络中的节点分成若干个群，两个节点是否链接的概率只取决于节点所在的群．用Ω 表示全体分群方案组成的集合，给定一个具体方案P∈Ω 和这个方案下一个具体的连边概率矩阵Q，一个随机分块模型M 就确定了，即M＝

（P，Q）．

以其中一种随机分块模型M3为例，该模型

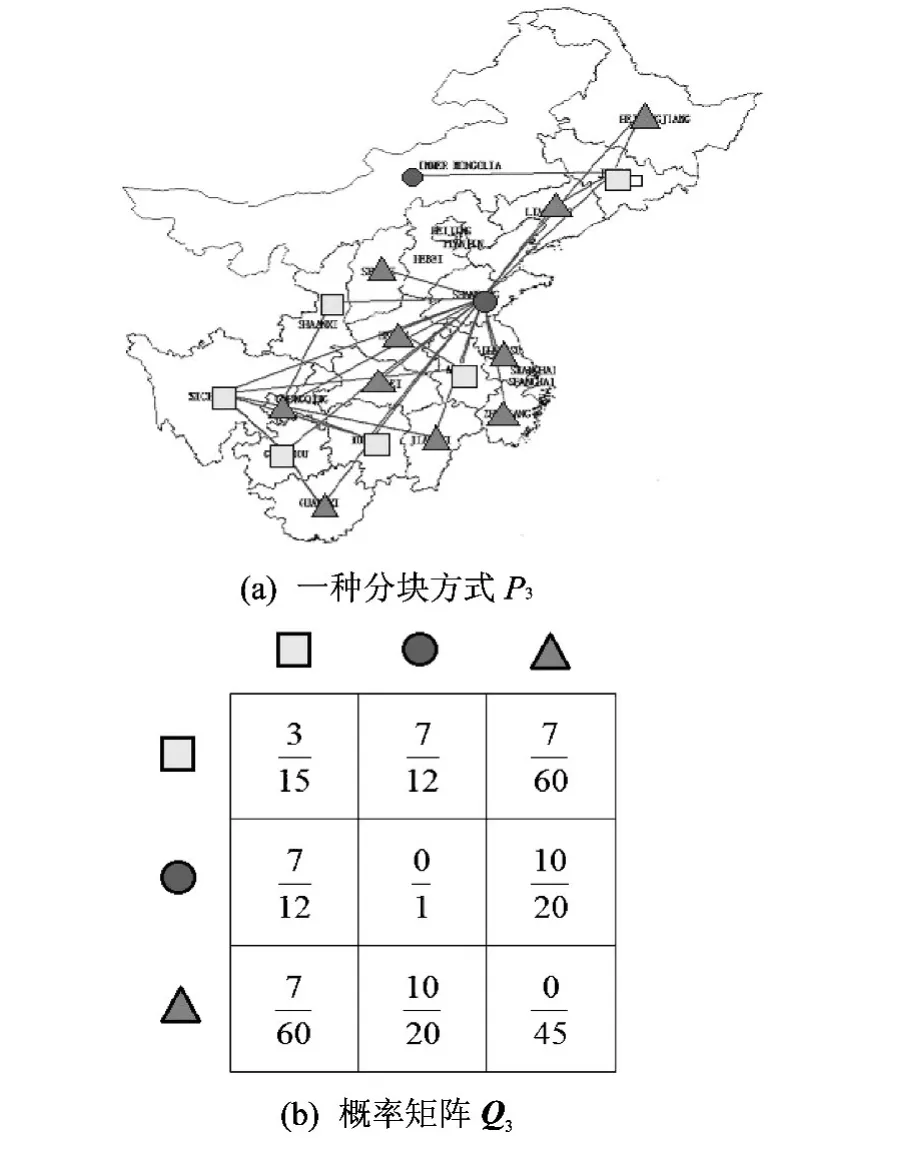
图4 随机分块模型M3Fig．4 Random block model M3

2．2 链路的信度

概率p（Axy＝1｜AO）可以用来表征链路｛vx，vy｝的信度［11，13］，

2.5 两组患儿并发症情况 对照组患儿并发症发生率25.0%(10/40),3例(7.5%)肺炎，2例(5.0%)肺不张，外心包积液、低心排血量综合征、败血症、瞳孔不等大、精神异常各1例(2.5%)。观察组并发症发生率4.8%(2/41),其中1例(2.4%)穿刺处血肿，1例(2.4%)封堵器脱落。

式中：｜Q｜是矩阵元素的数目，等于网络划分的群数的平方，而

对于某P 中的两个群α 和β，rαβ表示两个群中所有可能的连边数，lOαβ表示所观察到的网络AO中连接两个群α 和β 的连边数，则根据Beta函数积分公式，可以得到链路｛vx，vy｝信度的最终结果

式中：σx是节点vx所属群的编号；σy是节点vy所属的群的编号，

对于一个只有5个节点的网络，其分块方式都有77种，遍历18个节点所有可能的分块方式，其计算量是不可接受的．因此结合统计力学中总体均值的形式，使用大都市算法［18］来抽样相关分组更有利于得到链路信度的可靠性估计．首先把观测网络（见图3）中的18个节点每一个节点分别看作一组，每一步选择一个随机的节点并试图把它移动到一个随机的其他组，计算H（式（5））的变化．如果ΔH≤0，这个移动就被接受，否则，这个移动以exp（－ΔH）的概率被接受继续下一步移动，直到所有节点都移动到同一个组的时候循环结束，最终得到18种分块方式．

根据式（4），遍历以上18种分块方式即可求出网络中所有链路的信度．

2．3 网络重构

Guimera和Sales－Pardo设计了一个简单的贪婪算法［11，13］：首先将网络中所有的边按照信度排序，然后每次将信度最低的边删除，同时连接一条信度最高的边．此算法过程中，丢失边和虚假边的数目是相等的，这显然是不真实的．本文改进了贪婪算法，将“删边－加边”的操作分开进行．首先进行“删边”，每次将信度最低的一条边删除，这一操作仅当网络整体的信度增大的时候被接受．如果被拒绝，则对剩余边中信度最低的边继续进行上述过程，直到连续5次被拒绝后停止．然后进行“加边”，每次连接一条信度最高的边，这一操作也仅当网络整体的信度ħ（式7）增大的时候被接受．如果被拒绝，则对剩余边中信度最高的边继续进行上述过程，直到连续5次被拒绝后停止．

根据改进后的贪婪算法得到全国活羊调运网络缺失链路（见表1）和虚假链路（见表2），增加丢失链路，删除虚假链路就得到了一个新的网络，即全国活羊调运重构网络A（见图5）．此重构网络对于观测网络的可信度ħ＝（A｜AO）（式7）达到最大值．

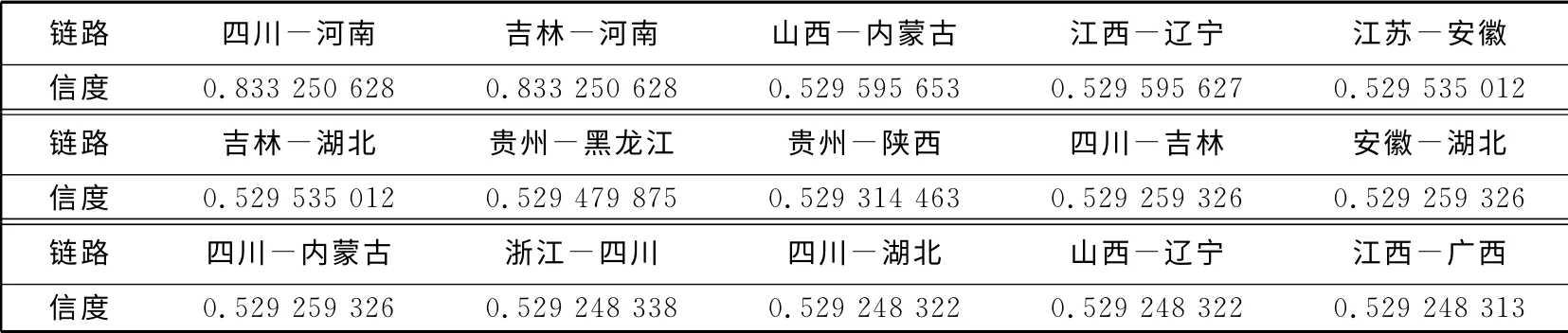
表1 缺失链路及其信度Tab．1 Missing link and its reliability

表2 虚假链路及其信度Tab．2 False link and its reliability

图5 全国活羊调运网络重构图Fig．5 Reconstructed network graph with national live sheep migration

在以上重构网络（图5）中，共有18 个节点，37条边．其中，节点山东的度为13，节点四川的度为9，节点吉林的度为6．66．7%的省份有3～4条连边．节点浙江的度最小．

由表1 可知，与河南有关的两条链路（四川－河南、吉林－河南）的信度较高．据调查，河南是我国主要的活羊集散地之一，全省有几十个规模较大的活羊交易市场，因此他们之间存在活羊调运的可能性较大．表2 中安徽－山东、贵州－山东这两条链路信度较低，可能因为安徽、贵州也是较大的活羊集散地，且他们与山东的羊养殖模式类似，所以存在活羊调运的可能性较小．由此看来，预测是符合实际的．

对以上的活羊调运网络重构过程进行了5次实验，5次实验得到的丢失链路与虚假链路完全相同．为进一步验证所得结果的可靠性，在重构网络中随机去掉一些保留路径，再随机加上同等数量的其他路径，得到了一个构造网络．利用以上方法，对构造网络进行网络重构，结果准确地预测出了去掉和增加的路径，还原了重构网络的面貌．可见，本文得到的活羊调运重构网络是比较可靠的．另一方面，根据市场调查和电话采访，山西与内蒙古之间确实存在活羊调运情况，这条链路在活羊调运观测网络中是不存在的，属于预测到的丢失链路．由此可知，本文得到的活羊调运重构网络是比较真实的．

3 结论与应用

本文根据2014年3月全国活羊调运信息，利用ArcGIS软件得到全国活羊调运观测图，根据随机分块模型和大都市算法，通过Matlab软件计算出网络中所有可能存在的链路的信度，运用改进后的贪婪算法得到观测网络中缺失的15条链路和虚假的5条链路，最终重构了全国活羊调运网络．

本文所得到的活羊调运重构网络，共有18个节点，37条边．其中，节点山东的连边数最多，其次是四川，吉林．显然这几个省份与其他省份的羊群贸易往来最多，疫情传播的风险最大．因此在疫病流行时，应从这几个省份开始采取相关措施，有效地切断传播途径，将疫病控制在一个有限的范围内，减少经济损失．除此之外，在此重构网络的基础上，还可以预测每个节点的感染途径，感染时间和染病概率，为制定动物疫病的防控措施提供了很好的依据．

以上活羊调运重构网络不仅适用于小反刍兽疫，也为研究其他羊类疫病（如布鲁氏菌病、口蹄疫等）提供了依据．

［1］Sarukkai R R．Link prediction and path analysis using markov chains［J］．Computer Networks，2000，33（1）：377－386．

［2］Zhu J，Hong J，Hughes J G．Using markov chains for link prediction in adaptive web sites［C］．Soft－Ware 2002：Computing in an Imperfect World．Springer Berlin Heidelberg，2002：60－73．

［3］Popescul A，Ungar L H．Statistical relational learning for link prediction［C］．IJCAI Workshop on Learning Statistical Models From Relational Data，2003：81－87．

［4］O’Madadhain J，Hutchins J，Smyth P．Prediction and ranking algorithms for event－based network data［J］．ACM SIGKDD Explorations Newsletter，2005，7（2）：23－30．

［5］Lin D．An information－theoretic definition of similarity［C］．ICML，1998（98）：296－304．

［6］Cannistraci C V，Alanis－Lobato G，Ravasi T．From link－prediction in brain connectomes and protein interactomes to the local－community－paradigm in complex networks［J］．Scientific reports，2013（3）：1－13．

［7］Li F，He J，Huang G，et al．A clustering－based link prediction method in social networks［J］．Procedia Computer Science，2014（29）：432－442．

［8］Liu W，LüL．Link prediction based on local random walk［J］．EPL（Europhysics Letters），2010，89（5）：58007．

［9］Clauset A，Moore C，Newman M E J．Hierarchical structure and the prediction of missing links in networks［J］．Nature，2008，453（7191）：98－101．

［10］Holland P W，Laskey K B，Leinhardt S．Stochastic blockmodels：First steps［J］．Social networks，1983，5（2）：109－137．

［11］GuimeràR，Sales－Pardo M．Missing and spurious interactions and the reconstruction of complex networks［J］．Proceedings of the National Academy of Sciences，2009，106（52）：22073－22078．

［12］Zhang X，Wang X，Zhao C，et al．Degree－corrected stochastic block models and reliability in networks［J］．Physica A：Statistical Mechanics and its Applications，2014（393）：553－559．

［13］吕琳媛，周涛．链路预测［M］．北京：高等教育出版社，2013．

［14］Karrer B，Newman M E J．Stochastic blockmodels and community structure in networks［J］．Physical Review E，2011，83（1）：016107．

［15］Ding J，Jiao L，Wu J，et al．Prediction of missing links based on multi－resolution community division［J］．Physica A：Statistical Mechanics and its Applications，2014．

［16］White H C，Boorman S A，Breiger R L．Social structure from multiple networks．I．Blockmodels of roles and positions［J］．American journal of sociology，1976：730－780．

［17］Anderson C J，Wasserman S，Faust K．Building stochastic blockmodels［J］．Social networks，1992，14（1）：137－161．

［18］Huang K．Statistical Mechanics［M］．New York：John Wiley ＆Sons，1987．