海洋中深度与压强的转换方法
2015-03-10冀天宇蒋国荣史剑周中刚邓波解放军理工大学气象海洋学院江苏南京0南京军区气象水文中心江苏南京0098解放军98部队广东湛江54000
冀天宇,蒋国荣,史剑,周中刚,邓波(.解放军理工大学气象海洋学院,江苏南京0;.南京军区气象水文中心,江苏南京0098; .解放军98部队,广东湛江54000)
海洋中深度与压强的转换方法
冀天宇1,蒋国荣1,史剑1,周中刚2,邓波3
(1.解放军理工大学气象海洋学院,江苏南京211101;2.南京军区气象水文中心,江苏南京210098; 3.解放军91338部队,广东湛江524000)
摘要:介绍了海洋学计算中3种深度与压强的转化方法:(1)EOS-80(Equation of State of Seawater 1980,EOS-80)标准采用的方法;(2)最新发布的TEOS-10(Thermodynamics Equation of seawater 2010,TEOS-10)标准采用的方法;(3)通过海水吉布斯函数计算压强与深度的关系的方法。对以上3种计算方法进行了比较,结果表明:在一般的海洋学研究中,3种方法精度相差不大,均可使用。在要求计算效率的情况下,可以选用EOS-80标准采用的方法,在更高精度的海洋学研究中,应该使用TEOS-10标准采用的方法或者吉布斯函数方法。
关键词:深度压强转换;海水吉布斯函数;EOS-80;TEOS-10
1 引言
海洋中压强与深度的换算关系是一种重要关系。在海洋调查仪器的观测资料处理中,需要将海洋调查仪器测量得到的压强转化为深度;在海洋理论研究,海洋模式计算中,由于密度是压强的函数,所以需要将等深度面上的格点资料中的深度值转化为压强值来计算密度。由于密度与压强存在对应的函数关系,所以对密度进行铅直向积分来计算压强存在困难。压强与深度的精确关系依赖于海水状态方程的精确表达式。Saunder根据1980海水状态方程(Equation of State of Seawater 1980,EOS-80),提出了一种实用的压强与深度的转换方法[1],并且被EOS-80标准所采用[2]。但是这一方法忽略了温度、盐度对深度与压强关系的影响。McDougall等根据最新提出的2010海水热力学方程(Thermodynamics Equation of seawater 2010,TEOS-10)提出了压强与深度转换的一种新方法[3],相比EOS-80标准而言包括了温度、盐度对压强与深度的关系的影响,并被TEOS-10标准所采用[4]。鉴于目前探讨海洋中深度与压强的转换关系的中文文献较少,本文对上述计算方法进行了介绍,并且在McDougall等工作的基础上,根据海水热力学定律[5],依据海水吉布斯函数,实现了压强转换为深度的吉布斯函数方法,并对以上三种计算方法进行了比较和讨论。
2 EOS-80采用的压强与深度的转换关系
2.1从深度到压强的转换
Saunders[1]给出了根据1980海水状态方程给出的实用的温度压强关系:
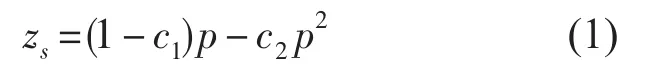
式中,c1=(5.92+5.25sin2ϕ)×10-3[mdb-1],c2= 2.21×10-6mdb-2。
根据(1)式得到(2)式,即为EOS-80标准采用的深度到压强的标准算法:
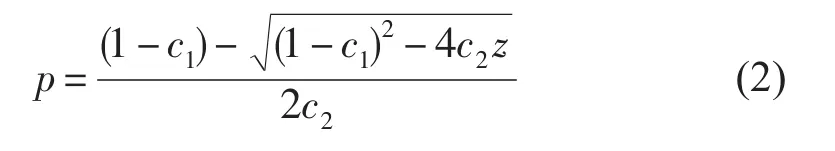
2.2从压强到深度的转换
EOS-80标准对从压强到深度的转换采取了拟合的方法,即
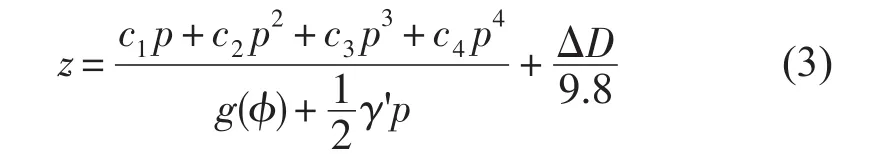
式中,c1=9.72659,c2=-2.2512×10-5,c3= -2.279×10-10,c4=-1.82×10-15,γ'=2.184×10-6ms-2/ db,ΔD=∫p0δdp',δ=ν(S,T,P)-ν(35,0,P),为比容偏差,g(ϕ)=9.780318(1.0+5.2788×10-3sin2(ϕ)+10-5× sin4(ϕ))[ms-2]。
(3)式中的比容偏差项要比第一项小两个量级[1],这说明在深度与压强的关系中,温度与盐度的贡献很小。EOS-80方法在压强转换为深度时略去了上式中的比容偏差项,一般而言这是可以接受的,但是在高精度的海洋学研究中,直接略去比容偏差项对深度与压强的关系的影响,势必会造成一定的误差。
3 TEOS-10采用的压强与深度的转换关系
TEOS-10是在一个完善的理论体系中建立起来的具有一致性和完备性的新方程,参考联合国教科文组织(United Nations Educational,Scientific,and Cultural Organization,UNESCO)对该方程的官方说明,TEOS-10方法在进行深度与压强关系的转换时,采用类似EOS-80方法的做法,首先对静力平衡方程=-ρg进行垂直积分,得到:
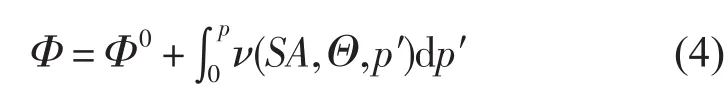
式中,Φ代表重力位势,SA代表绝对盐度,Θ代表守恒温度(绝对盐度、守恒温度的定义、同实用盐度和摄氏温度的转化参考UNESCO对TEOS-10的官方说明[4])。
Feistel和Hagen(1995)导出了海水的吉布斯函数[6],可以用来求解包括内能,熵,比容,声速,位温等一些热力学变量。Mcdougall对该吉布斯函数进行了拟合,提出了包含25项的计算海水密度的表达式,并且被TEOS-10标准所采用[7]。该密度的拟合表达式能够直接对比容进行积分,从而直接求解出海水的比焓。与EOS-80标准中采用的方法不同,该方法在计算比容的铅直积分时没有略去比容偏差的贡献。这样,温度、盐度对深度与压强的关系的影响就包括在了表达式中。对(4)式进行积分后有:
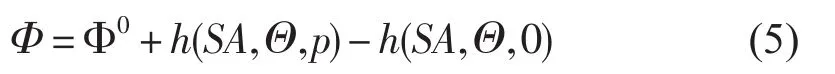
式中,h(SA,Θ,p)代表海水的比焓,Φ代表海水重力势。根据Mcdougall拟合的25项密度计算公式可以直接求得海水的比焓[4],即h(SA,Θ,p),进而得到深度与压强的关系。
在进行从深度到压强的转换时,TEOS-10方法根据上述从压强到深度的转换关系,采用Mcdougall等提出的改进的Newton-Raphson迭代方法[8]求解从深度到压强的转换关系,其本质上的原理同样是Mcdougall等拟合出的,用于计算密度的25项表达式。
4 根据海水的吉布斯函数计算深度与压强的关系
TEOS-10相对于EOS-80最大的区别就是利用海水的吉布斯函数计算海水的各种性质。热力学理论现在已经证明:如果一个热力学系统基本方程是已知的,那么通过相应的微分和代数运算就能够求出整个系统的各种热力学性质。目前虽然没法直接计算得到海水的吉布斯函数,但是可以分别求解出海水中水和盐的吉布斯函数[5]。
首先定义比吉布斯能函数g,表示单位质量海水的吉布斯能。其与海水的质量无关。海水的比吉布斯能可以视为海水中纯水的比吉布斯能和盐的比吉布斯能之和,即:
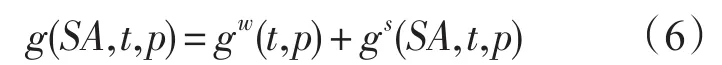
ν表示比容。根据热力学关系:
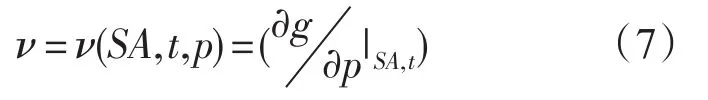
可以求得比容对压强的积分为:
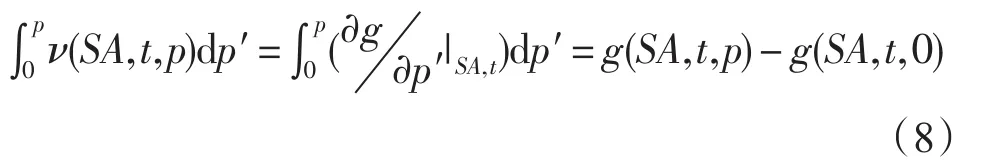
积分形式的海水静力平衡方程为:
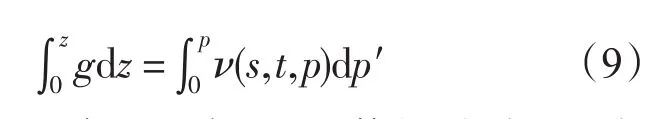
式中,ν表示比容。根据1979修订公式,重力加速度随着纬度和深度变化,即g=gs+γz,gs代表重力加速的地球表面值,是纬度的函数。gs与纬度的关系由下式给出:
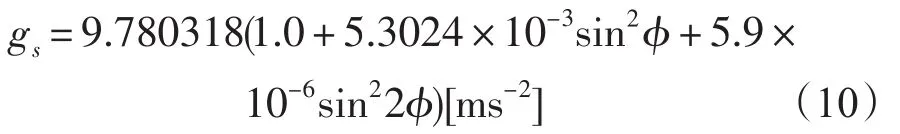
带入(9),得到:
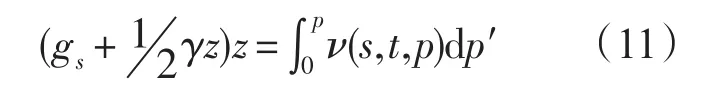
引入压强修正项(Saunders,1981),根据SA与S的转化关系:
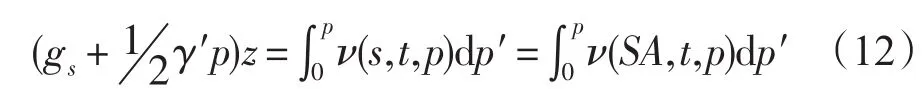
式中,γ′=2.226×10-6ms-2/db。
根据(8)和(11)式可以得到压强、深度的转化关系:
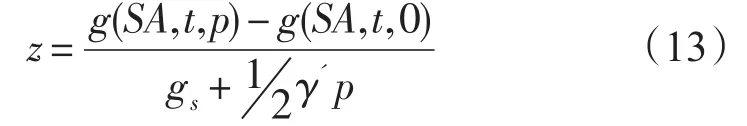
式中,海水的吉布斯函数g为多项式的形式,其系数可以参考UNESCO发布的TEOS-10官方使用手册[4]。
由于压强变量是海水的吉布斯函数的一个自变量,在求解从深度到压强的关系便会遇到困难。因此吉布斯函数方法只适于求解从压强到深度的换算关系。
5 计算结果的对比和讨论
海洋研究中常用简单的线性关系进行压强与深度之间的换算,即:

式中,p0为标准大气压,ρref为参考密度,取为1025 kg/m3。为了说明每种方法的计算精度,本文根据WOA09(World Ocean Atlas 2009)气候态平均资料,选取分别选取太平洋,印度洋,大西洋中的三个站点,其经纬度坐标分别为(173.5°E,30.5°N),(29.5°W,26.5°N),(75.5°E,15.5°S)。所选站点的温盐垂直分布曲线见图1。表1至表4列出了不同方法的计算结果。

图1 所选择站点的温度、盐度垂直分布
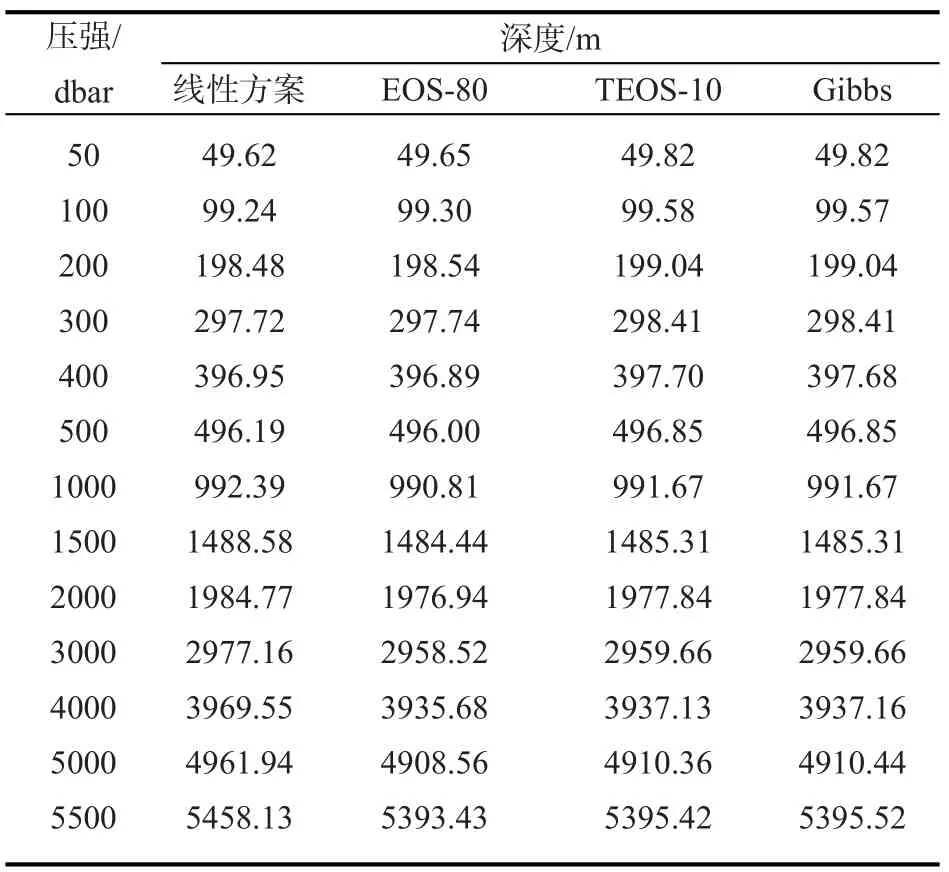
表1 太平洋中部站点压强转化为深度的结果的比较
表1、表2的第一列是常用的深度与压强的线性关系的计算结果,比较几种不同方法的计算结果,可以看出采取线性关系计算海洋中的压强与深度关系与其他方法相比还是存在比较大的差异的,这种差异在海洋表层较小,随着深度的增加而增加,最大差值能够达到7%。鉴于公式(1)的简洁性,完全可以采用EOS-80标准使用的方法来估算海洋中深度与压强的关系。
表1的第三四列表示在所取站点的温盐分布的情况下,不同压强条件,TEOS-10标准采用的计算方法和吉布斯函数计算方法计算结果的差值(其余站点结果相似,未列出)。两种方法的计算原理同属于热力学框架。从表1中可以看出,在小于2000 db的压强条件下,这两种方法的计算结果几乎完全一致,随着深度的增加,一直5500 db的深度,二者的计算差值仅为0.2 m左右,因此可以说明根据吉布斯函数的计算压强到深度的转换关系的方法是可行的,适用的。
表3和表4分别表示使用EOS-80方法和TEOS-10方法进行深度与压强转换的计算结果的差值。从压强转换为深度的结果来看(见表3),这两种方法的差值最大为2 m左右。从深度转化为压强的结果来看(见表4),这两种方法计算差值最大为150 db左右,但是在海洋中上层,这两种方法的计算差异比较小。因此在不同的计算精度要求下,尤其是在将深度转为压强的计算中,两种方法的计算差异还是要考虑的。
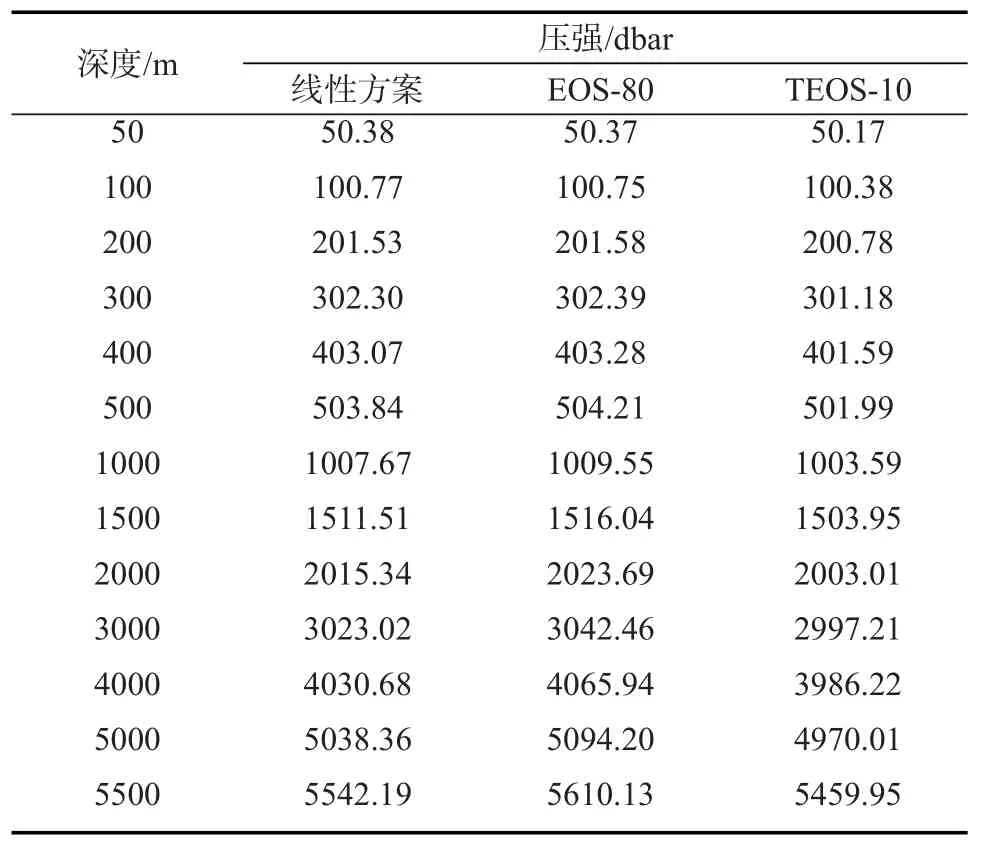
表2 太平洋中部站点深度转化为压强的结果的比较
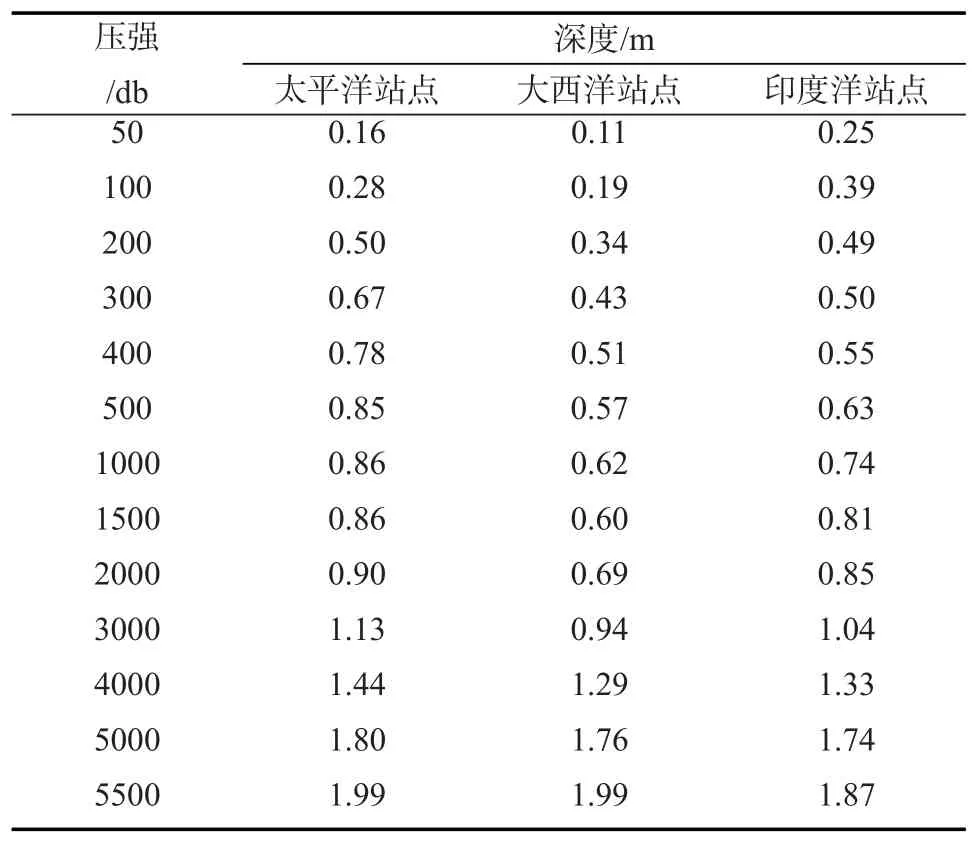
表3 三个站点上使用TEOS-10方法和EOS-80方法将压强转化为深度的结果的差值
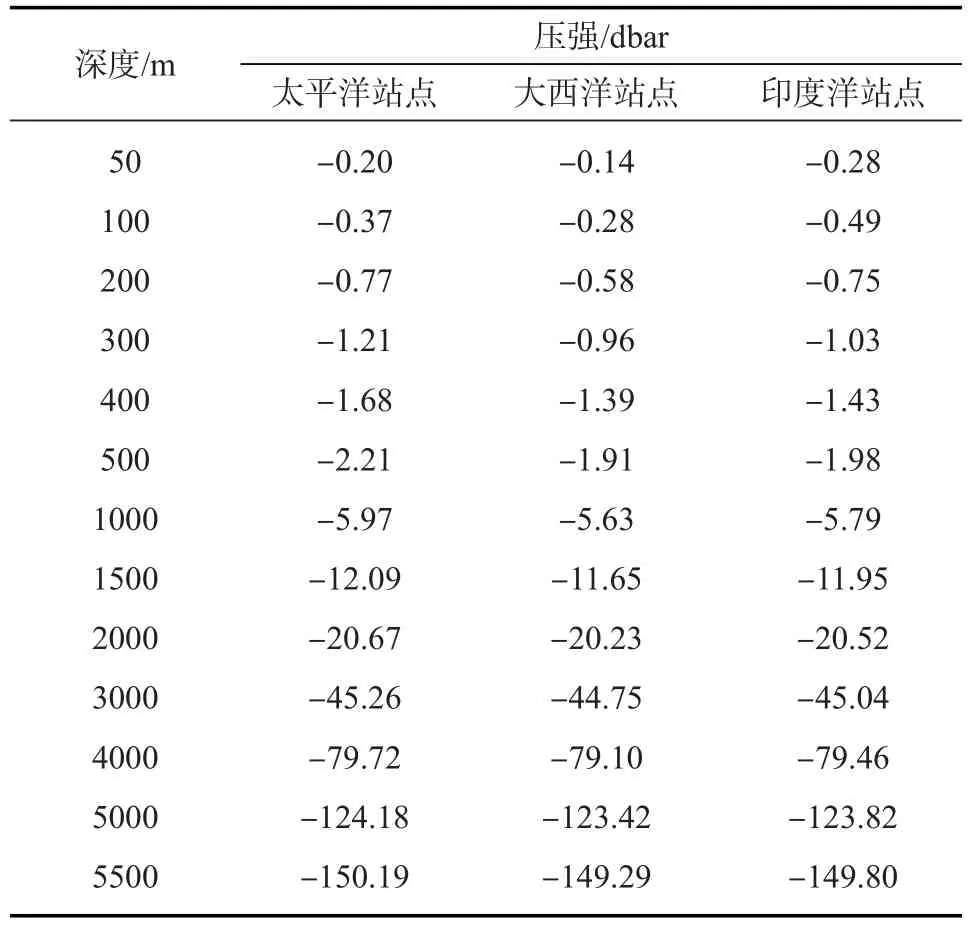
表4 三个站点上使用TEOS-10方法和EOS-80方法将深度转化为压强的结果的差值
造成这两种计算结果的差异的原因在于EOS-80方法计算深度与压强的关系时略去了比容偏差项ΔD=∫0pδdp'(见公式3),从而建立了深度与压强的直接关系。Saunder[1]计算后认为比容偏差项对深度与压强关系的影响比压强的改变对深度与压强关系的影响要小两个量级,可以不予考虑。TEOS-10方法采用Mcdugall等根据海水吉布斯函数拟合出的25项表达式计算深度与压强的关系,比容偏差项对深度压强转换关系的影响包括在比容对压强的积分中(见公式5),从理论上而言,TEOS-10标准更为精确。使用吉布斯函数计算深度与压强的关系同样能够将比容偏差项的影响包含在比容对压强的积分内(见公式8)。从这一点上看,TEOS-10方法和吉布斯函数计算方法要比EOS-80的计算方法更为精确。比容偏差项是温度、盐度与压强的函数。众所周知,海洋中上层是温度盐度变化剧烈的水层,从表3、表4中可以看出,在不同站点的中上层,这两种不同方法的计算差异还是比较小的。这是因为温度、盐度的变化对比容偏差的影响较小。而随着深度与压强的增加,这两种计算方法的差值也逐渐增加,这是因为压强的变化对比容偏差项影响较大,从而造成了表3表4所示的差异。
根据以上讨论,对于一般的海洋学研究,采用EOS-80和TEOS-10方法均可,也可采用吉布斯函数方法。TEOS-10标准方法和吉布斯函数方法相对EOS-80标准方法而言,在将深度转化为压强时,计算精度有明显提高,但同时计算过程也较复杂。在有些计算资源紧张的场合下(比如在嵌入式设备中),为了权衡计算精度和计算效率之间的矛盾,可以采用EOS-80标准所采用的方法。如果在精度要求更高的情况下,应该采用TEOS-10标准使用的方法或者本文使用的吉布斯函数计算的方法。
6 结论
本文讨论了三种深度与压强相互转化的方法,并比较了三者的差异。在一般的海洋学研究中,这三种方法均可以使用。在注重计算效率的情况下,可以使用EOS-80标准所使用的方法,在精度要求更高的海洋学研究中,应该使用TEOS-10标准使用的计算方法,如果只需要将压强转换为深度,吉布斯函数计算方法也是可行的。
参考文献:
[1] Saunders P M. Practical conversion of pressure to depth [J]. Journal of Physical Oceanography, 1981, 11: 573-57.
[2] ICES, SCOR, IAPSO. The Practical Salinity Scale 1978 and the International Equation of State of Seawater 1980 [R]. UNESCO Technical Papers in Marine Science No 36, 1981: 25.
[3] McDougall T J,Barker P M. Getting started with TEOS-10 and the Gibbs Seawater(GSW)Oceanographic Toolbox 2010 [ SCOR/ IAPSO WG127][R].2011.28.
[4] IOC, SCOR, IAPSO. The international thermodynamic equation of seawater-2010: Calculation and use of thermodynamic properties [J]. Intergovernmental Oceanographic Commission, Manuals and Guides, 2010, 56: 196.
[5] Sun Y M, Shi J X, Yang H P. The thermodynamic equation of seawater 2010 and its comparison with the equation of seawater 1980 [J].Advance in Earth Science, 2012, 27(9): 1014-1025.
[6] IAPWS. Release on the IAPWS Formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use[A].Fredericia,1996.
[7] Jackett D R, McDougall T J, Feistel R, et al. Algorithms for density, potential temperature, conservative temperature, and the freezing temperature of seawater [J]. Journal of Atmospheric and Oceanic Technology, 2006, 23: 1709-17128.
[8] McDougall T J, Wotherspoon S J. A simple modification of Newton’s method to achieve convergence of order 1 +√2 [J]. Applied Mathematics Letters, 2014, 29: 20-25.
[9]姚勇,卫薇,陈华秋. 90国际温标对80国际海水状态方程影响的研究[J].海洋技术, 2001, 20(3): 74-78.
[10] Bacon S, Fofonoff N. Oceanic heat flux calculation [J]. Journal of Atmospheric and Oceanic Technology, 1996, 13(6): 1327-1329.
[11] Feistel R, Weinreben S, Wolf H, et al. Density and absolute salinity of the Baltic Sea 2006-2009[J]. Ocean Science, 2010, 6 (1): 3-24.
[12] Jackett D R, McDougall T J, Feistel R, et al. Algorithms for density, potential temperature, conservative temperature, and the freezing temperature of seawater[J]. Journal of Atmospheric and Oceanic Technology, 2006, 23(12): 1709-1728.
Conversion methods of depth and pressure in the ocean
JI Tian-yu1, JIANG Guo-rong1, SHI-Jian1, ZHOU Zhong-gang2, DENG Bo3
(1. Insititude of Meteorology, PLA univ. of Sci. & Tech., Nanjing 211101 China; 2. Mete-hydrological center of Nanjing Military Region, Nanjing 210016 China; 3. 91388 PLA troops, Zhanjiang 524000 China)
Abstract:Three conversion methods of depth and pressure in the ocean are described. (1) Method adopted by EOS-80 standard (Equation of State of Seawater 1980, EOS-80); (2) Method adopted by TEOS-10 standard (Thermodynamics Equation of seawater 2010,TEOS-10); (3) Convert pressure to depth via the Gibbs function of seawater. After comparison of three methods, the results show that, in general oceanographic research, the three methods can all be used in general oceanographic research, according to their similar accuracy. However, the EOS-80 method should be adopted in the request of computational efficiency, and the TEOS-10 method or Gibbs function method should be taken in the high-precision oceanographic research.
Key words:conversion between depth and pressure;Gibbs function;EOS-80;TEOS-10
作者简介:冀天宇(1989-),男,硕士研究生,主要研究方向为海洋动力学与数值模拟。E-mail:414203624@qq.com
基金项目:国家自然科学基金(41106014);江苏省自然科学基金(BK20131066)
收稿日期:2014-06-10
DOI:10.11737/j.issn.1003-0239.2015.02.007
中图分类号:P733
文献标识码:A
文章编号:1003-0239(2015)02-0045-06
