基于实验数据的有效性分析滑动变阻器的特性
2015-03-10赵清锋
赵清锋
基于实验数据的有效性分析滑动变阻器的特性
赵清锋
(孝昌县第一高级中学,湖北 孝昌 432900)
基于方差理论,提出了物理实验数据的有效性评估方法,给出了数据有效率的计算公式;分别讨论了分压电路与限流电路中待测电阻两端的电压U随滑动变阻器调节比例l(x)之间的关系,并分析了数据的有效率与k(滑动变阻器总阻值与待测电阻的阻值之比)之间的关系,同时提出了不同电路中滑动变阻器的选择以及选择后的调节技巧;最后以数据的有效性为基础将分压电路和限流电路进行比较分析.
滑动变阻器;分压电路;限流电路;方差
1 引 言
分压电路与限流电路是电路理论的基础,也是电学实验的重点,对于分压电路与限流电路中滑动变阻器的特性在文献[1-4]中已有讨论,但是定量的标准以及调节的技巧目前尚未有专门的分析. 基于此,本文从数据的有效性角度出发,以方差理论为基础提出了物理实验数据的有效性评估方法;然后分别讨论了电学实验中比较重要的分压电路与限流电路中待测电阻两端的电压U随滑动变阻器调节比例l(x)之间的关系,分析了数据的有效性与k(滑动变阻器总阻值与待测电阻的阻值之比)之间的关系,并借助Matlab绘图加以形象描述,同时提出了不同电路中滑动变阻器的选择以及选择后的调节技巧;最后结合数据的有效率将分压电路和限流电路进行比较分析.
2 实验数据的有效性评估
在电学实验中,实验数据的有效性至关重要,有效性如果较低会导致误差的增加. 文中以方差理论为基础,提出了数据有效性的评估方法.
随机变量X的方差表达了X的取值与其数学期望的偏离程度,根据定义,对于离散型随机变量有[5]:
D(X)=∑∞k=1[xk-E(X)]2pk,
其中P{X=xk}=pk,k=1,2,…是X的分布律. 因此,方差D(X)是刻画X取值分散程度的一个量,它是衡量X取值分散程度的一个尺度.
而在物理实验中,通常需要得到均匀分布的数据(或指定位置的数据),但是由于实验器材的影响,得到的数据并不均匀(或偏离指定位置),由此就会出现数据的有效性问题,基于此本文结合方差的概念,类比给出数据有效性的评估方法. 首先给出数据的不均匀程度:
D(X)=∑N-1k=1|xk-Xk|pk,
其中pk指实验数据xk的分布律,Xk指第k个实验数据的理想位置,xk指第k个实验数据的实际位置,N为数据的组数,XN-X1为数据的范围.D(X)反映了实验数据的均匀程度,D(X)越小表明所取的数据分布越均匀. 应该注意的是此处D(X)与方差中的概念有所不同,此处用绝对值反映其偏离程度.
进而给出实验数据有效性的评估函数(数据有效率)为
A(X)=1-D(X)(xN-x1)∑N-1k=1pk×100%.
(1)
按照式(1)计算,数据的有效率越大表明实验数据越理想,且有效率可以取0到100%之间的任意值,以方便定量分析.
3 分压电路中滑动变阻器的特性
设滑动变阻器的最大阻值为R0,且总长度为l,设接入ap段的长度为x,则滑动变阻器ap段的电阻为xlR0,pb段的阻值为l-xlR0,ap段的电阻与待测电阻Rx并联,再与pb段的电阻串联,电源的电动势为E,忽略其内阻,如图1所示.ap段与Rx并联部分的电压为
U=xlRxl2Rx+xlR0-x2R0E.
(2)
令k=R0Rx,l(x)=xl[l(x)∈(0,1)],将(2)式分子分母同时除以Rxl2,化简如下:
U=l(x)1+kl(x)-kl(x)2E.
(3)
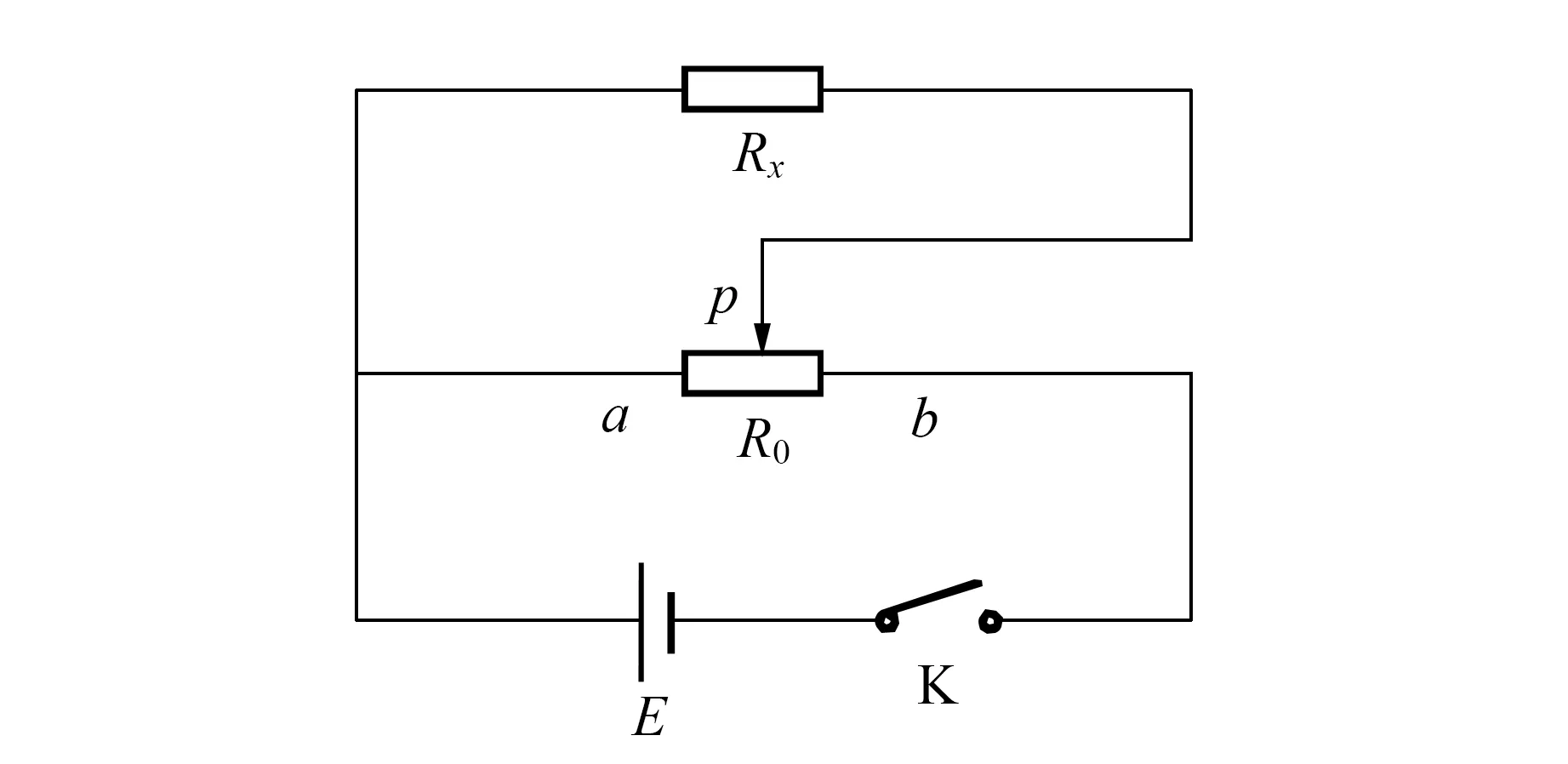
图1 分压电路图
当k=0.1,0.5,1,2,5,10,20,分别作出UE-l(x)图像如图2所示.

图2 分压电路中不同k值UE -l(x)图像
从图2中可以看出,随着k的增加,图线逐渐变得弯曲,离直线UE=l(x)的最远距离也在逐渐地增加,结合(1)式,可作出数据有效率A(x)随k的变化关系如图3所示.

图3 数据有效率A(x)随k值的变化关系
从图3中可以看出,随着k的增加,数据有效率逐渐降低,数据的有效率A(x)与k的关系列举如表1所示.

表1 k-A(x)关系
按照实验中调节滑动变阻器的习惯,均匀地调节滑动变阻器然后读取数据,按照此方法取不同的k值均匀调节10次,读取电压数据,用一维坐标描述如图4所示(k与表1中的数据对应).

图4 不同k值情况下均匀调节10次得到电压数据分析
从图4中可以看出当k较小时,均匀调节滑动变阻器所得电压数据分布比较均匀,而当k较大时,所测数据就比较分散,数据有效性降低,这样必然导致最终作图误差较大,尤其是在描绘小灯泡的伏安特性曲线实验中.
所以在采用分压电路时应该选择较小的滑动变阻器,这样所测的数据有效性才更好,若实验中确实没有这样的滑动变阻器,则在调节滑动变阻器的过程中应在l(x)=xl较大的位置调节幅度减小,这样可以使调节过程中读取的数据尽量均匀,从而提高数据的有效性.
4 限流电路中滑动变阻器的特性
与分压电路相似,设滑动变阻器的最大阻值为R0,总长度为l,设bp段的长度为x,则ap段的电阻为l-xlR0,ap段的电阻与待测电阻Rx串联,如图5所示.
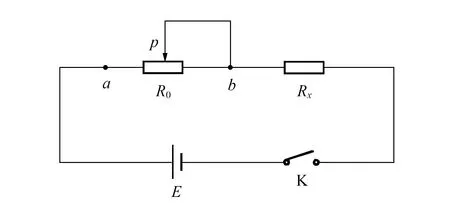
图5 限流电路图
待测电阻所分得的电压为
U=lRxlRx+(l-x)R0E.
(4)
令k=R0Rx,l(x)=xl,将(4)式分子分母同时除以Rxl,化简如下:
U=11+k-kl(x)E.
(5)
当k=0.1,0.5,1,2,5,10,20,分别作出UE-l(x)图像如图6所示.

图6 限流电路中不同k值对应UE与l(x)之间的关系
从图6中可以看出,k越小滑动变阻器的调节范围越小,调节范围UE∈11+k,1;随着k的增加图线逐渐变得弯曲,也就是数据的均匀程度在逐渐地减小. 因此在采用限流电路时,既要让数据分布比较广又要让数据分布比较均匀是不可能的. 限流电路通常用于测量待测电阻的阻值,同等条件下比分压电路输出功率小,更节能.
结合本文中所给数据有效率的计算式,可作出数据有效率A(x)随k的变化关系如图7所示.
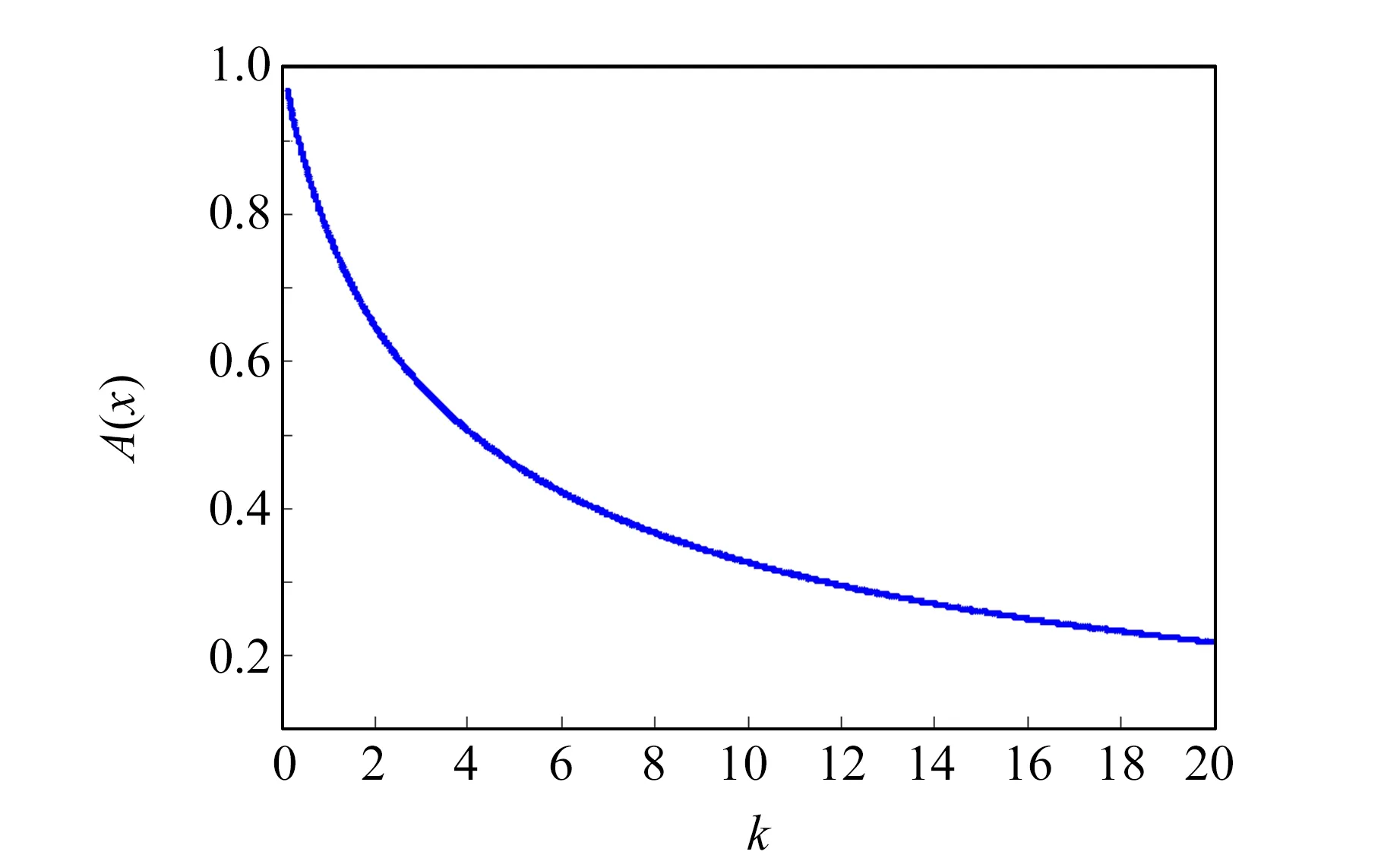
图7 数据有效率A(x)随k值的变化关系
从图7中可以看出,随着k的增加,数据有效率逐渐减小. 在此取不同的k值均匀调节滑动变阻器10次读取电压数据用一维坐标描述如图8所示.
从图8中可以看出当k较小时,均匀调节滑动变阻器所得电压数据分布比较均匀,但数据的分布范围较小;而当k较大时,所测数据比较广,但分布很不均匀,数据有效率降低.
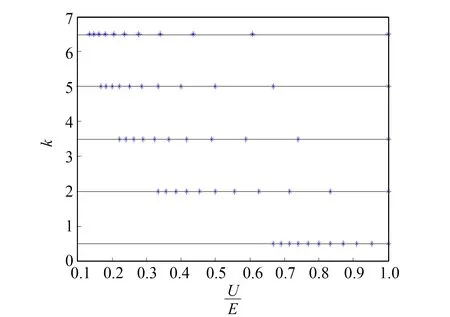
图8 不同k值情况下均匀调节10次得到电压数据分布
5 分压电路与限流电路的比较
从2种方案的图像进行分析可以发现,当滑动变阻器与待测电阻比值k较大时,在调节滑动变阻器的过程中,分压电路ap段的电阻Rap与待测电阻的阻值Rx比较接近,与限流电路效果相当. 在分压电路中Rap=l(x)Rx1/k+l(x),当k值较大时,Rap≈Rx. 作出k=0.5,2,10,20,50情况下Rap/Rx随l(x)的变化如图9所示.

图9 Rap/Rx与l(x)的关系
从图9中可以看出,当k=50时,当l(x)较小时变化很快,而当l(x)接近0.1时,Rap/Rx几乎接近1,也就是说对于滑动变阻器其绝大多数调节区域没有用到,或者说在调节的过程中只有很小的区域内调节是有效的,而实验者的习惯是均匀地调节,这样得到的数据有效性将会很低. 当k值较大时,分压电路与限流电路效果相当,取k=10画出分压电路与限流电路UE与l(x)的关系如图10所示.

图10 k=10时UE随l(x)的变化关系
另外,从数据的有效性分析,分压电路和限流电路数据的有效性都随着K值的增加而减小,现将2种电路中数据的有效率图像放在一起分析如图11所示.
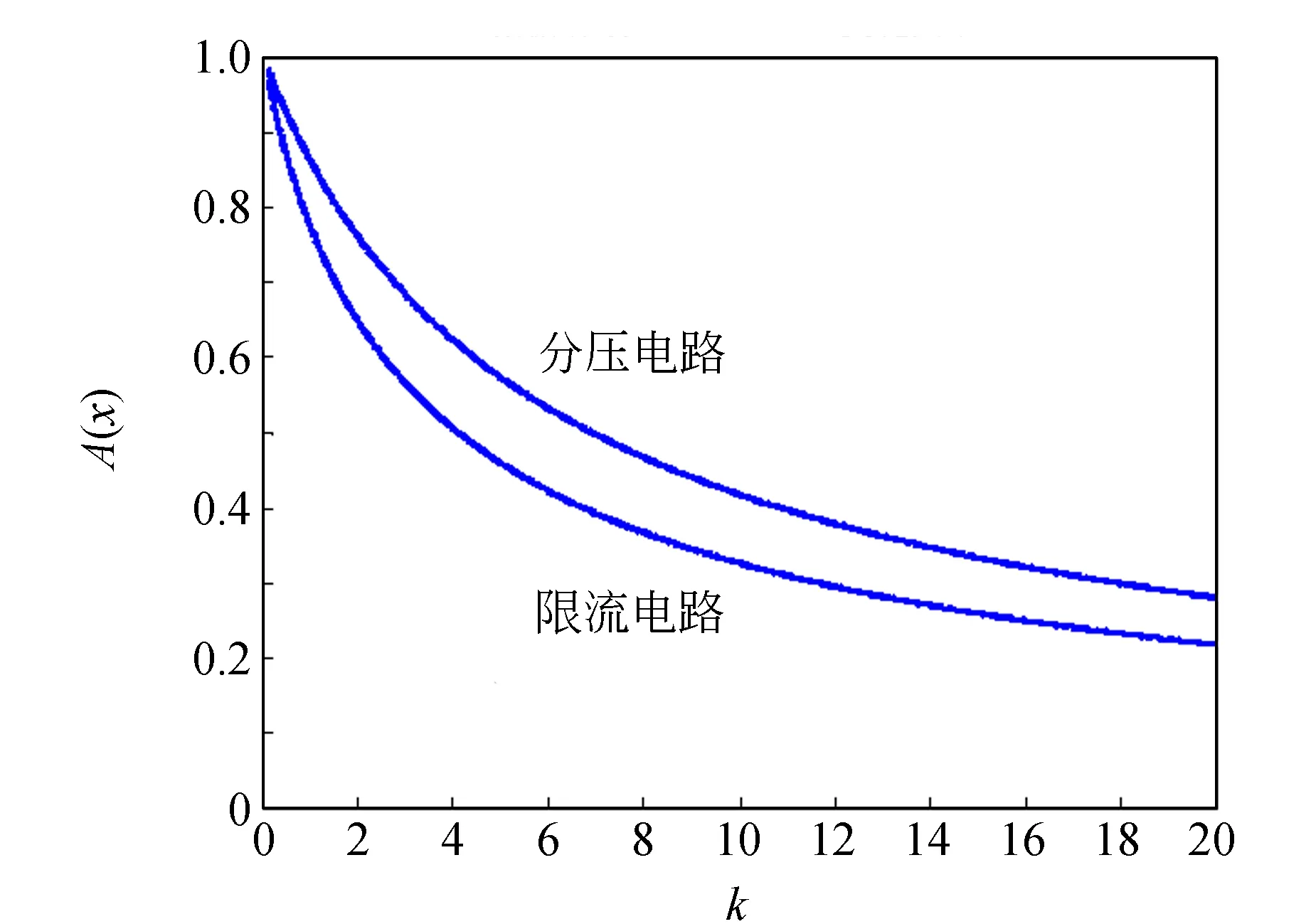
图11 数据有效率A(x)随k值的变化关系
从图11中可以看出,按照本文给出数据有效率的定义,分压电路数据的有效率总是比限流电路高,又由于限流电路所测数据范围较小,因此在选择电路时,若不考虑功率的因素,分压电路比限流电路效果好.
6 结束语
通过分析发现同等条件下分压电路数据的有效率总比限流电路的高,数据测量范围广,因此不考虑功率的因素选择分压电路更好. 数据的有效率是类比方差理论给出,目的在于衡量实验数据的分布理想程度(本文主要用于衡量数据均匀分布程度),设计有效率的公式可以达到到中间的任意数据,以方便定量的评估,但有效率的公式还有待进一步完善.
[1] 徐立海. 用图像分析限流和分压接法中滑动变阻器的选取[J]. 物理实验,2006,26(2):27-29.
[2] 穆晓东. 制流与分压电路实验参数的选择与确定[J]. 大学物理实验,2004(1):34-36.
[3] 徐成华. 分压电路的电压输出特征[J]. 物理教学,2010(8):29-31.
[4] 徐荣广. 实验探究分压电路中负载电阻的电压变化[J]. 物理实验,2013,33(3):21-23.
[5] 盛骤,谢式千,潘承毅. 概率论与数理统计[M]. 北京:高等教育出版社,2008:100-101.
[责任编辑:尹冬梅]
Analyzing the characteristics of slide rheostat based on the validity of experimental data
ZHAO Qing-feng
(Xiaochang No.1 High School, Xiaochang 432900, China)
Based on error theory,an evaluation method of the validity of physics experiment data was presented, a compute formula on data validity was put forward. The relationships between the voltage on the resistor and the adjustment of the slide rheostat in bleeder circuit or current-limiting circuit were discussed; the dependence of the data validity onk(the ratio between the resistance of the resistor being tested and the total resistance of the slide rheostat) was analyzed. Some key points on the selection and adjustment of slide rheostat were suggested, and finally, bleeder circuit and current-limiting circuit were compared based on data validity.
slide rheostat; bleeder circuit; current-limiting circuit; variance
2015-01-06
赵清锋(1988-),男,湖北襄阳人,湖北省孝昌县第一高级中学二级教师,学士,主要研究方向为物理实验设计与分析.
G633.7
A
1005-4642(2015)06-0015-04
