煤矿瓦斯涌出量动态预测的PCA-MFOA-GRNN模型及应用*

2015-03-10皮子坤贾宝山贾廷贵李宗翔

传感技术学报 2015年11期

皮子坤，贾宝山*，贾廷贵，李锐，李宗翔

（1.辽宁工程技术大学安全科学与工程学院，辽宁阜新123000；2.矿山热动力灾害与防治教育部重点实验室，辽宁阜新123000）

我国是产煤大国，煤炭在我国能源消耗中占一次性能源的70%左右［1］。随着我国煤矿开采深度和生产能力不断加强，矿井瓦斯问题成为严重制约煤矿安全生产的重要因素之一［2］。对矿井绝对瓦斯涌出量进行精准预测，提前采取必要的防治措施是预防煤矿瓦斯灾害事故和减少人员与财产损失的关键。国内外许多学者对煤矿瓦斯涌出量预测进行了大量研究。肖鹏、李树刚等运用灰色理论对煤矿瓦斯涌出量进行建模及其预测研究［3］；张淑玲、崔洪庆等运用灰色关联理论对矿井瓦斯涌出灾害进行预测研究［4］；吕伏、梁冰等采用主成分回归分析法对回采工作面瓦斯涌出量进行预测［5］；罗景峰、许开立运用模糊数学理论，采用可变模糊组合方法对瓦斯涌出量进行预测［6］；朱红青、常文杰等运用BP神经网络，结合分源预测法对回采工作面瓦斯涌出量进行预测［7］；何利文、施式亮等运用时间序列与混沌理论，对回采工作面瓦斯涌出预测方法研究［8］。这写方法及其预测模型各具特点，但在预测精度方面，相对误差较大，存在一定的局限性。煤矿瓦斯涌出受到煤矿本身地质条件、所采取的开采工艺技术等诸多因素共同作用，直接导致煤矿瓦斯涌出量精确预测方面难度加大。近些年兴起的人工神经网络［9-10］在非线性拟合方面取得了一定的成果，但在收敛性及泛化能力上都存在一定的缺陷，如训练速度过慢，容易陷入局部最小值等。

鉴于此，笔者提出建立基于PCA-MFOA-GRNN相耦合的预测模型，对回采工作面的瓦斯涌出量进行预测。

运用PCA算法，对影响矿井瓦斯涌出的影响因素进行前期处理，这些因素之间存在的相关性会给模型带入很多冗杂因子信息，致使模型的预测准确度和泛化能力都较低，而主成分分析法的降维技术可以减小模型变量，最大程度消除变量间的冗杂信息。提高了预测模型的准确率与稳定性。

对果蝇算法中的Si函数增加一个跳脱参数B进行改进，避免了局部最优因子对预测模型的干扰，再将MFOA算法对GRNN的平滑因子σ进行优化；将PCA结果作为模型的输入，建立了PCA-MFOAGRNN的耦合预测模型，并应用于实际煤矿当中，验证了该模型瓦斯涌出预测的精确性与可靠性。

1 相关理论

1.1 PCA基本理论

主成分分析（PCA）是利用降维的思想，在力保数据信息损失最少的原则下，把多个指标转化为少数几个综合指标的一种对多变量数据进行最佳综合简化的多元统计方法。

假设有n个样本，每个样本观测p个指标，记为X=(x1,x2,…,xp)′。变量X的均值为μ，协方差矩阵为Σ。则：

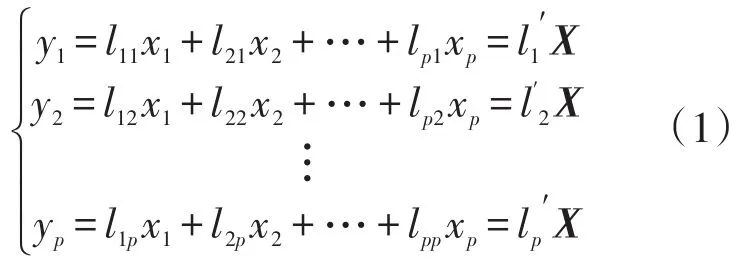
1.2 GRNN基本原理

广义回归神经网络(GRNN)是一监督式的学习方式网络。1991年，Donald F.Specht提出了这个学习算法［11］，GRNN算法是由机率类神经网络所演变而来，不需要像传统回归分析一样先假设一个明确函数形式，只需要以机率密度函数的方式呈现。这个算法不只可以做分类问题，也可以用来学习动态模式并做预测或控制，而且对于线性或非线性的回归问题都有很好的处理能力。GRNN由于人为调节参数很少，只有一个阈值，网络的学习全部依赖数据样本，从而得以最大程度地避免了人为主观假定对预测结果的影响。

GRNN神经网络的创建需要将所有数据划分为输入向量、输出向量、训练数据和测试数据，如图1所示。

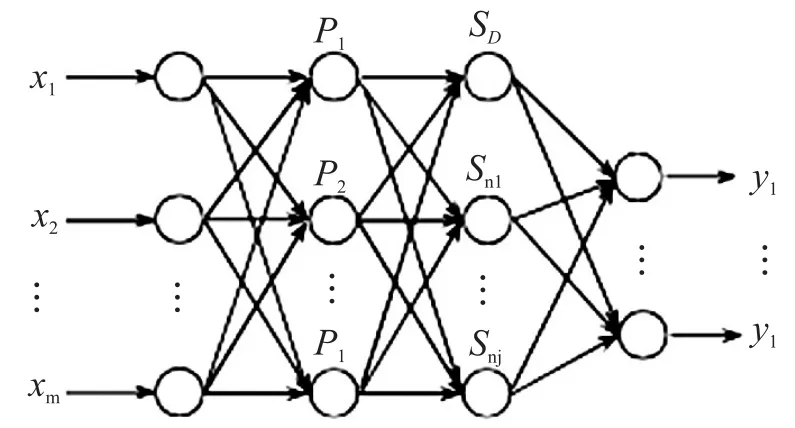
图1 GRNN结构示意图

设自变量为x，因变量为y，定义x、y的联合概率密度为f(x,y)，条件概率密度为：

则得到x的条件平均值y（也称为y在x上的回归）

联合概率密度函数满足高斯分布

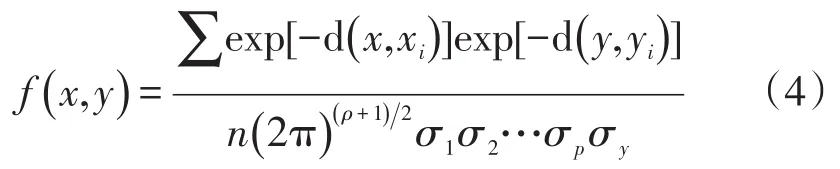
式中：xi和yi是训练集内的输入和输出，σ为宽度函数，σ满足下列趋势：

将（6）式代入（4）式整理后得，

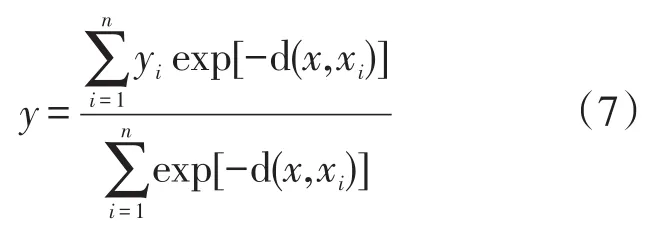
对于多因变量的问题，假设每个因变量均与自变量满足高斯分布，则每个因变量均可用式（7）计算出来。

1.3 FCA-MFOA优化GRNN的参数

果蝇优化算法（FOA）是台湾学者潘文超提出的，是一种基于果蝇觅食行为寻求全局优化的新算法［12-13］。果蝇能灵敏的嗅到40 km以外食物飘散在空气中的气味，通过估计周围味道浓度，随后朝着味道浓度极值方向飞去，重复迭代味道浓度寻求目标函数的最优解［14-15］。由于FOA算法容易陷于局部极值，无法找寻到全局极值，笔者将Si函数增加一个跳脱参数B，以此对果蝇算法进行修正，得到修正的果蝇算法（MFOA），如式（8）所示。通过增加该参数，使整个算法不但能跳脱局部极小值找到全局极值，Fitness function函数也能够取到负值，避免算法无法取负值的缺陷。

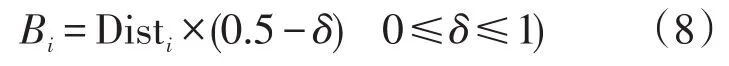
修正的FOA算法（MFOA）具体运算步骤如下：

①果蝇群体初始化，果蝇随机初始位置为(X_axis,Y_axis)，种群规模为sizepop=10，迭代次数为maxgen=100；②对果蝇个体随机赋值（方向和距离），Xi=X_axis+rand,Yi=Y_axis+rand；③刚开始果蝇不知道目标具体位置，因而先估计果蝇个体与原点的距离D，同时计算味道浓度判定值S，；④计算出果蝇个体在该处的味道浓度值，smell(i)=F(Si)；⑤寻找出果蝇群体中味道浓度最大值[best Smell best index]=max(Smell)；⑥保留最佳味道浓度值与该果蝇坐标，Smell best=bestSmell,X_axis=Xbestindex,Y_axis=Ybestindex；⑦进入迭代寻优，重复②～⑤，并判断味道浓度是否优于前一迭代味道浓度，若是，则执行步骤⑥，否则继续下一次迭代循环，直到达到最大循环次数时才停止。

具体运算流程如图2所示。

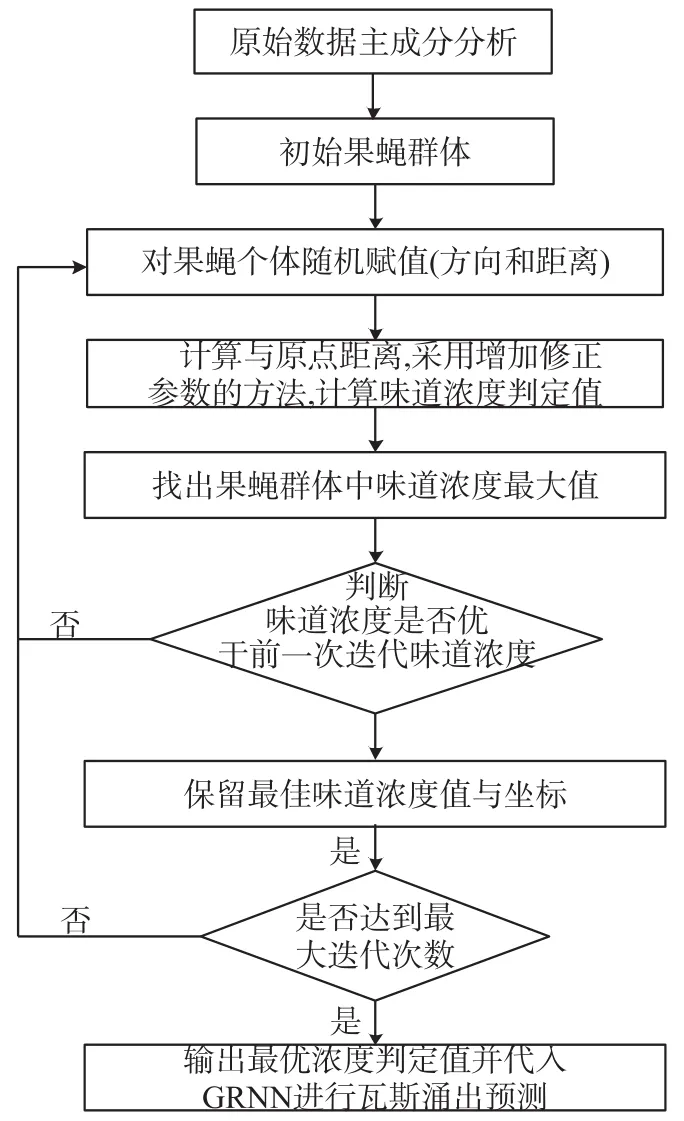
图2 FCA-MFOA优化GRNN流程图

2 预测模型的建立

2.1 模型样本数据的选择

笔者选取文献［10］提供的瓦斯涌出相关数据来进行建模及预测，煤层瓦斯含量X1，m3/t、煤层埋藏深度X2，m、煤层厚度X3，m、煤层倾角X4，°、采高X5，m、采煤工作面长度X6，m、推进速度X7，m/d、采出率X8，%、临近层瓦斯含量X9，m3/t、临近层厚度X10，m、临近层层间距X11，m、层间岩性X12、开采强度X13，t/d、顶板管理方式X14，X1～X14为影响工作面瓦斯涌出量Y的主要因素，选取表1中1～15组数据作为训练集样本，16～18组作为测试集样本，如表1所示。

2.2 瓦斯涌出影响因素的主成分分析

在影响瓦斯涌出量的因素中，煤层厚度与采高一致，故在主成分分析中，只选因素X3，而工作面顶板的管理方式均相同，对分析结果没影响，所以不考虑X14因素。运用SPSS 21.0软件对表1数据进行主成分分析，分析结果如表2所示。

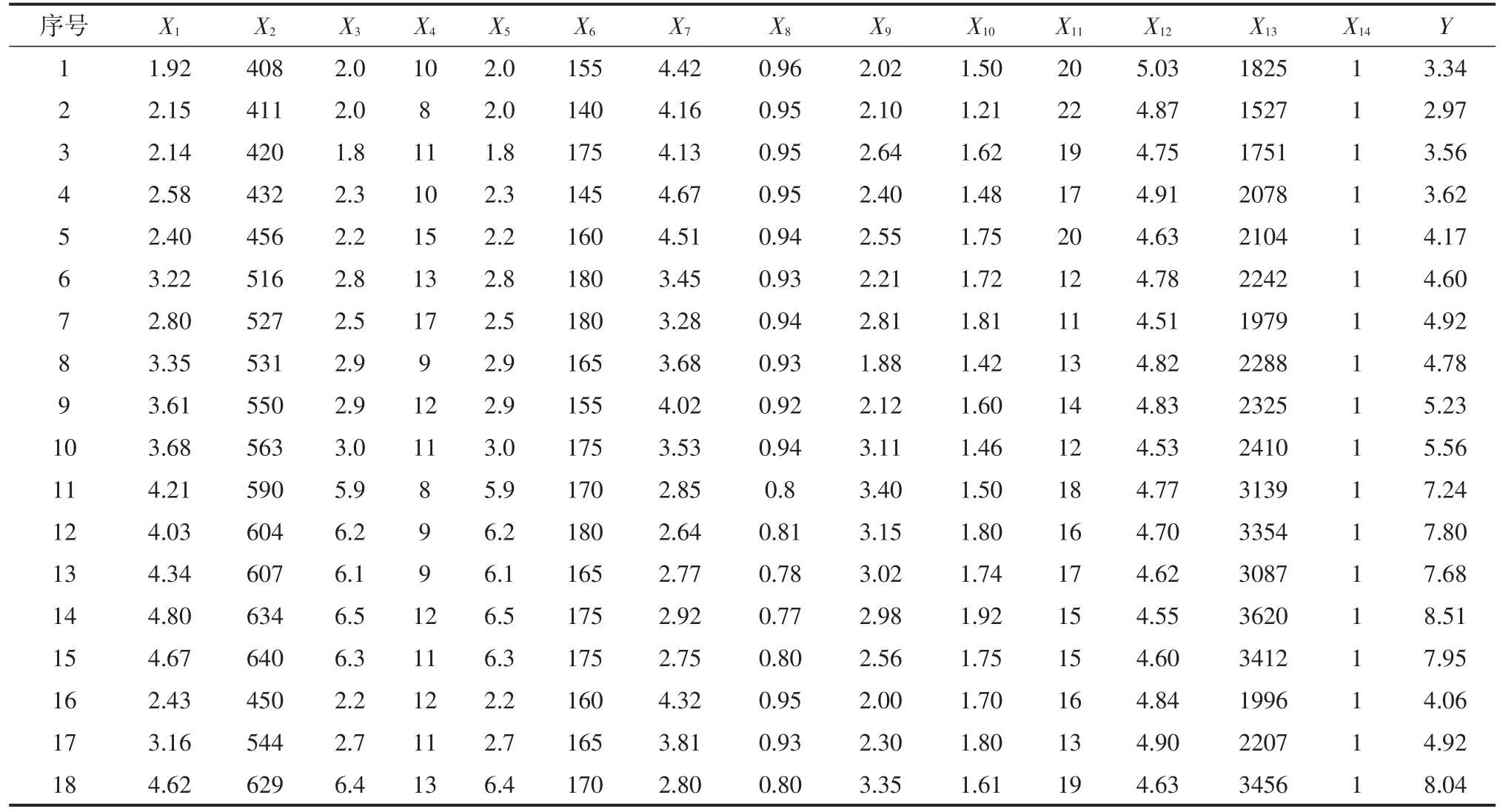
表1 回采工作面瓦斯涌出量影响因素数据统计

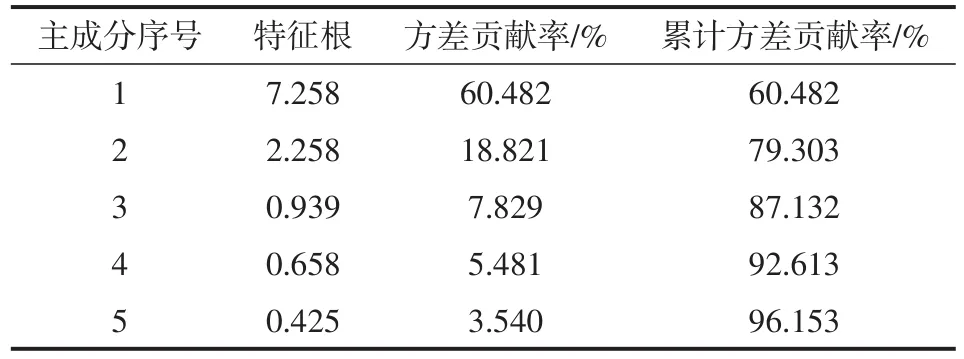
表2 主成分分析方差贡献表

由表2可得，主成分分析结果的前4个主成分累计方差贡献率为92.613%，说明这4个主成分已经包含了这13个影响因素中的绝大部分有效信息。为了保证预测模型的精确度，笔者选取前5个主成分，累计方差贡献率为96.153%，作为预测模型的输入。这5个主成分的得分系数如表3所示，由表3数据计算得这5个主成分，结果如表4所示。

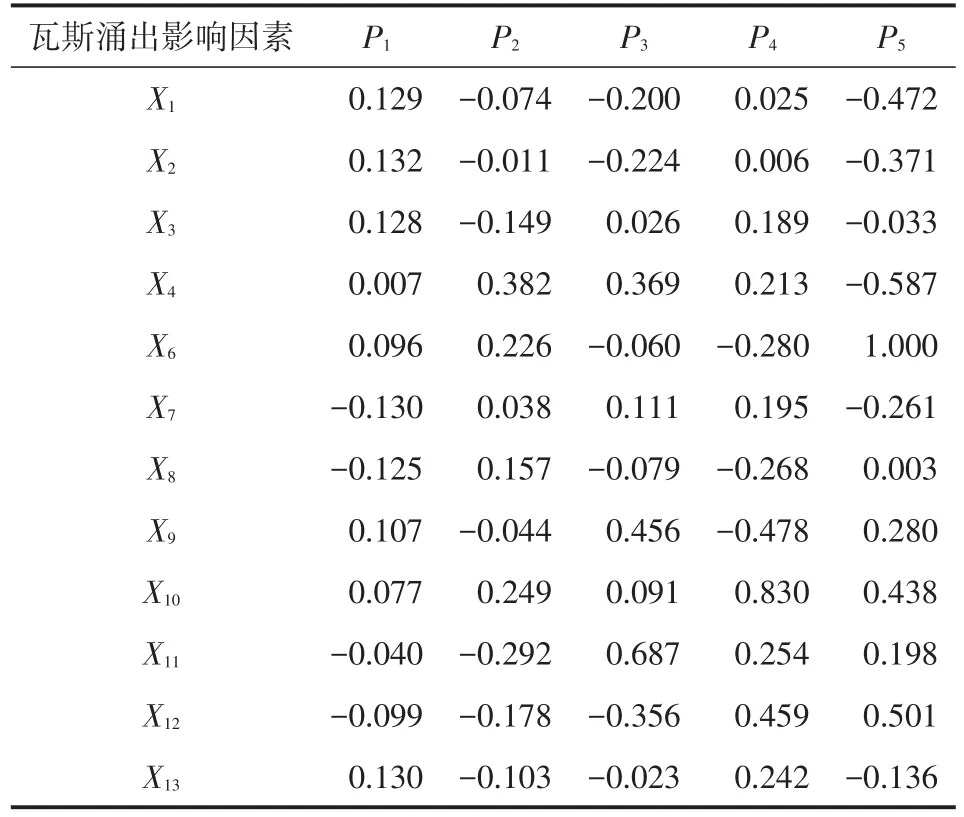
表3 前5个主成分得分系数

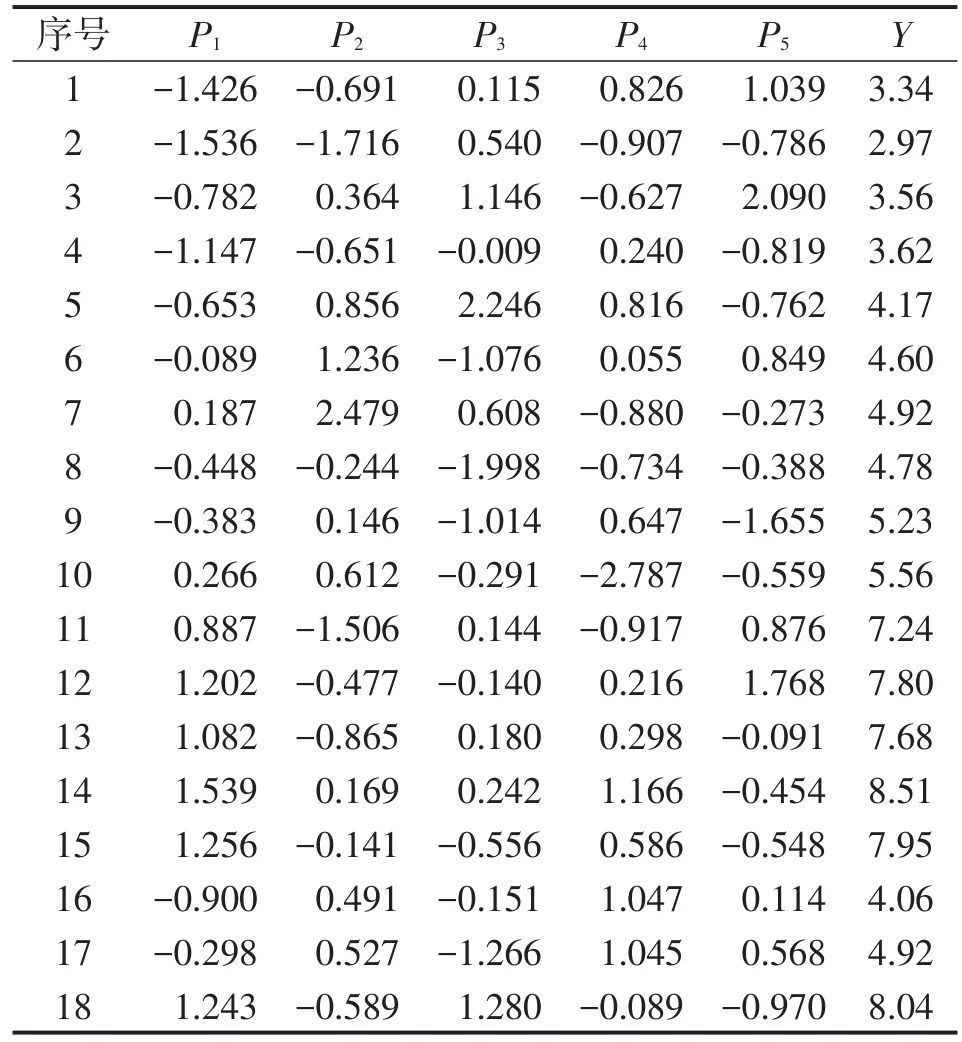
表4 前5个主成分

对瓦斯涌出量影响因素进行PCA降维处理，提出特征信息，有效减少了瓦斯涌出因素变量的数量，简化了各变量之间的关系。将5个瓦斯涌出综合影响因素作为预测模型的变量，避免了各因素间复杂的非线性问题对模型的干扰。

2.3 PCA-MFOA-GRNN工作面绝对涌出量预测

运用Matlab软件，将表4中P1～P5作为输入向量，Y为输出向量，建立PCA-MFOA-GRNN综采工作面瓦斯涌出动态预测模型。选取表1中1～15组数据为预测模型的训练集，16～18组数据作为检验模型算法性能的数据集。

在广义回归神经网络预测模型中，平滑参数σ，即Spread参数值与神经元数、训练样本有关。合理的优化Spread参数值，直接影响模型的预测性能。文中应用MFOA算法对GRNN的Spread参数值进行合理调整优化。经由MFOA的100次迭代动态调整GRNN后RMSE收敛情况，如图3所示，在迭代优化过程中RMSE在第62个世代收敛，RMSE=0.056 69，计算对应的最佳Spread参数值为0.057 6。

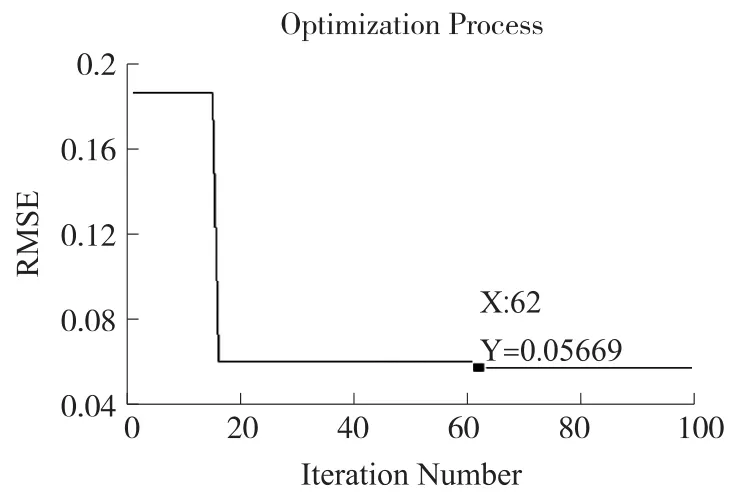
图3 MSE收敛情况

运用前面所训练好的预测模型将测试集样本输入向量输入该模型，进行预测运算，如图4所示。图4为预测模型的预测值与实测值对比图。

图4 PCA-MFOA-GRNN模型测试数据预测结果对比

2.4 预测模型检验分析

为了检验PCA-MFOA-GRNN动态预测模型的预测性能的可靠性，本文运用未修正的FOA-GRNN算法、CIPSO-ENN算法、BP神经网络预测、Elman网络预测，这4种算法的预测结果与之对比，结果如表5所示。

表5 五种预测模型预测效果对比

由表2可知，PCA-MFOA-GRNN预测模型的预测值分别为：4.067 5、4.857 7、7.829 6，相对误差分别为：0.185%、1.267%、2.617%，平均相对误差为1.357%，相比其他四种算法所计算出的预测值，PCA-MFOA-GRNN预测模型平均相对误差均小于其最小，达到理想的预测效果。

3 结论

①提出了基于主成分分析（PCA）与修正的果蝇算法（MFOA）优化GRNN算法的煤矿综采工作面瓦斯涌出动态预测模型（PCA-MFOA-GRNN）。运用主成分分析对影响瓦斯涌出因素进行降维处理，得出的5个主成分作为预测模型的输入，同时对FOA算法Si函数增加一个跳脱参数B，避免了局部最优因子对预测模型的干扰，提高了预测模型的稳定性与预测精确度。

②利用该模型的预测结果与其他4算法的预测结果相比较，该模型预测精度最高，为煤矿瓦斯涌出量预测提供一个有效的方法。

③影响煤矿综采工作面瓦斯涌出量的因素很多，本文仅收集了14个方面的数据进行计算分析，从科学严谨与广泛推广的角度，应该采集更加全面的影响因素数据，使本模型更具普遍使用意义。

［1］王涛，王洋洋，郭长娜，等.QGA-RBF神经网络在矿井瓦斯涌出量预测中的应用［J］.传感技术学报，2012，25(1)：119-123.

［2］付华，刘雨竹，李海霞，等.煤矿瓦斯浓度的CAPSO-ENN短期预测模型［J］.传感技术学报，2015，28(5)：717-722.

［3］肖鹏，李树刚，宋莹，等.瓦斯涌出量的灰色建模及其预测［J］.采矿与安全工程学报，2009，26(3)：318-321.

［4］张淑玲，崔洪庆，刘国兴，等.灰色关联理论在矿井瓦斯涌出灾害预测中的应用［J］.煤炭技术，2008，27(3)：67-69.

［5］吕伏，梁冰，孙维吉，等.基于主成分回归分析法的回采工作面瓦斯涌出量预测［J］.煤炭学报，2012，37(1)：113-116.

［6］罗景峰，许开立.基于可变模糊组合方法的瓦斯涌出量预测［J］.中国安全生产科学技术，2011，7(6)：29-32.

［7］朱红青，常文杰，张彬.回采工作面瓦斯涌出BP神经网络分源预测模型及应用［J］.煤炭学报，2007，32(5)：504-508.

［8］何利文，施式亮，宋译，等.基于支持向量机（SVM）的回采工作面瓦斯涌出混沌预测方法研究［J］.中国安全科学学报，2009，19(9)：42-46.

［9］曲健，陈红岩，刘文贞，等.基于改进网格搜索法的支持向量机在气体定量分析中的应用［J］.传感技术学报，2015，28(5)：774-778.

［10］付华，姜伟，单欣欣.基于耦合算法的煤矿瓦斯涌出量预测模型研究［J］.煤炭学报，2012，37(4)：654-658.