T-形磁通集聚器磁场放大特性及影响因素研究*

吕忆玲，张晓明，2*，陈国彬，樊之琼

（1.中北大学电子测试技术重点实验室，太原030051；2.中北大学仪器科学与动态测试教育部重点实验室，太原030051）

磁通集聚器结构由高磁导率的软磁材料制成。在磁场环境中，高磁导率材料具有汇聚磁力线的作用。该作用能够使得高磁导率材料内部磁场强度大于外部环境磁场强度。在现阶段常用的微型磁传感器精度低，无法满足地磁场环境中弱磁场高灵敏度高精度的测量需求。因此在现有磁传感器的基础上外加磁通集聚器结构能够提高现有磁传感器的灵敏度，提高弱磁场的测量精度和灵敏度。相比于信号调理电路增大灵敏度，磁通集聚器利用放大环境磁场特性增大磁传感器的灵敏度，该方式不会影响传感器电路系统的测量噪声［1］。软磁材料具有很小的矫顽力以及剩磁，因此磁通集聚结构产生的放大磁场随外部环境磁场的变化具有较好的线性度以及较小的滞后特性。

磁通集聚器结构能够将外部磁场中的磁通收集起来并将其聚集在一个较小空间中。相比于外部环境磁场，该空间中分布的磁场具有较大的磁通量密度，因此磁通集聚器具有能够放大外部磁场的功能。Menitt N.Deeter利用两块圆台体的高磁导率软磁材料作为磁通集聚器增大光纤磁传感器的灵敏度［2，3］。在不同形状的磁通集聚器中，具有圆台体形状的磁通集聚器在其轴向的放大特性最好。但随着微加工技术的不断发展，一些磁性器件以及磁阻类磁传感器的制备都向着微米级甚至纳米级的方向发展［4］。但是现阶段微加工技术很难实现三维圆台体的制备，因此用于微型磁传感器的磁通集聚器都是具有特定形状的二维薄片结构［5］。Schneider利用CMOS工艺制备了基于坡莫合金材料的漏斗状磁通集聚器，实验表明该结构能够有效增大磁敏晶体管的灵敏度［6］。Simon B及Drljaa P M等人针对不同形状的磁通集聚器磁场放大特性进行了仿真初步的分析，分析表明T-形磁通集聚器对外部磁场的放大效果最好［7，8］。Sansheng W及Xiaoguang Y等人利用磁通集聚器来提高微型磁传感器的性能，结果证明它能提高微型传感器的线性度［9，10］。但现阶段主要基于仿真分析磁通集聚器结构轴向磁场放大特性及影响轴向磁场放大因素，针对其结构轴向磁场放大特性及影响轴向磁场放大因素的试验测试较少，因此本文在基于ANSYS仿真分析的基于上再加上试验测试进行分析。

本文在分析高磁导率磁场集聚放大理论的基础上，利用ANSYS仿真软件主要针对T-形磁通集聚器对外部磁场轴向放大性能进行分析；并分析研究T-形磁通集聚器的磁导率、空气间隙、长宽之比和结构厚度对外部磁场放大倍数的影响；最后设计相应的磁通集聚器进行试验测试。

1 高磁导率材料磁场集聚放大理论分析

磁通集聚器的制备材料通常是高磁导率软磁合金材料，当这类材料处于一个均匀的外部磁场环境H0中时，在其磁化过程中其内部会产生一个与外部磁场H0方向相反的叠加磁场，该磁场称为材料的退磁强度，其与磁化强度的关系为［11］

其中，M为磁化强度，N为材料的退磁因子，范围在0和1之间，该退磁因子与材料的形状尺寸参数有关，对于一般形状的材料其三轴方向上的退磁因子是不同的，材料内部不同位置的退磁因子也是不同的。则在软磁材料的内部，磁场强度等于［12］

μ0是真空的相对磁导率，Jm为软磁材料的磁感应强度。Jm等于［12］

μr为材料的相对磁导率，可以得到磁通集聚器内部的磁感应强度Bin等于

其中μeff为材料的有效磁导率，则［12］

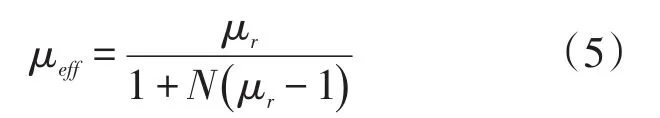
从式（5）中可以看出，材料的有效磁导率μeff与材料的相对磁导率μr以及材料的退磁因子N有关。当材料相对磁导率μr趋向于无穷时，其有效磁导率μeff趋向于最大值为

可以看出随着材料相对磁导率μr逐渐增大，其变化对有效磁导率μeff的变化影响逐渐减小，因此在相对磁导率大于某一阈值时，材料的有效磁导率就主要由其退磁因子所决定。又由于退磁因子材料结构的形状参数有关，从而可以得出材料的有效磁导率由材料的形状参数所决定。对于具有左右对称形状的高磁导率材料来说，当其处于均匀稳定的磁场环境中时，其内部中间位置的磁感应强度是最大的。如在该材料中间对称轴位置将其切割为两个相同的对称结构，其对称结构之间缝隙位置的磁感应强度也要大于环境中磁感应强度。但该磁感应强度小于在切割之前的整体材料内部中间位置的磁感应强度，主要由于缝隙使在材料内部分布的磁通产生了向环境中的磁通泄漏，其缝隙宽度越宽，泄露的磁通量就越多，从而导致缝隙位置的磁感应强度越小。因此，在其缝隙宽度足够小的情况下，可以认为将双对称结构缝隙位置的磁感应强度与整体结构内部中间位置的磁感应强度一致。因此，当Bgap为空气间隙的磁感应强度，B0为外部磁感应强度时，双对称结构间隙位置的磁感应强度放大倍数可以表达为［13］

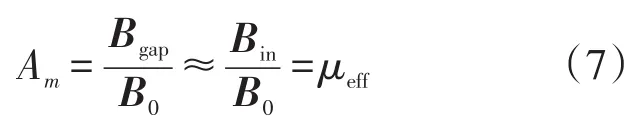
2 T-形磁通集聚器轴向磁场的分析

通过磁场集聚放大理论分析，本文首先分析未加空气间隙及带有空气间隙T-形磁通集聚器轴向磁场仿真分析，如图1、图2所示。

图1 未加空气间隙的T-形磁通集聚器

图2 带有空气间隙的T-形磁通集聚器

利用ANSYS有限元软件对磁通集聚器进行静态磁场仿真分析，加载与x轴平行的外部均匀磁场，仿真结果如图3所示。

图3 未加及带有空气间隙的磁通集聚器轴向磁场强度

从图3可以看出，对于未加空气间隙隔开的磁通集聚器来说，磁通集聚器内部的磁场强度最高值位于结构的中间点。为了使磁传感器能够测得中间点位置的磁场强度，利用长度为1 mm的空气间隙把磁通集聚器从中间位置隔开使其成为对称结构。具有对称结构的磁通集聚器对外部磁场的放大特性具有对称性。对于单个磁通集聚器来说，结构内部最大磁场强度同样位于结构的中间位置。相比于隔开之前的磁通集聚器结构内部中间位置的磁感应强度，空气间隙中间点位置的磁场强度较小。这是由于磁通集聚器集聚外部磁力线时，磁力线在从结构一端到另一端流动的过程中并不是始终在磁通集聚器的内部，而是在其流动过程中产生了磁通泄漏现象，如图4所示。但相对于外部磁场强度，空气间隙中间点位置对外部磁场放大效果同样较为明显。此仿真结果与磁场集聚放大理论分析相一致。

图4 T-形磁通集聚器磁力线图

根据以上的分析可知，磁通集聚器一般设计成对称结构，如图5所示。

图5 T-形磁通集聚器示意图

利用有限元软件对磁通集聚器静态磁场仿真分析，结构具体尺寸如表1所示。

表1 T-形磁通集聚器具体尺寸参数 单位：mm

仿真实体结构模型包括双对称磁通集聚器结构与空气区域，双对称磁通集聚器置于空气区域内部的中心位置。仿真过程中，选用SOLID96单元类型，在材料属性设置时分别设置磁通集聚器及空气区域的相对磁导率为100 000和1；其次，建立仿真结构模型、网格划分、加载与x轴平行的外部磁场强度，大小为50 000 nT；最后进行求解，利用路径法提取x轴方向上点的坐标及对应点的BX、BY、BZ强度，如图6所示。

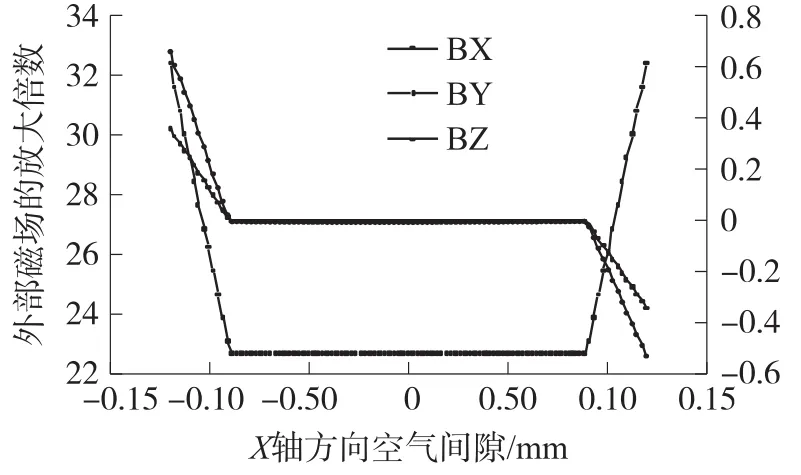
图6 磁通集聚器结构空气间隙轴向磁场

从图6可以看出，磁通集聚器对周围环境磁场具有集聚、放大作用，空气间隙轴向磁场对外部磁场的放大倍数同样具有对称性。通过分析得，T-形磁通集聚器对外部磁场放大了22.5倍。当加载沿x轴方向上的平行磁场时，理论上轴向BY、BZ强度等零。但由于磁通经过磁通集聚器的空气间隙时，在空气间隙的边缘区域产生了磁通泄漏现象，如图7所示。因此，在空气间隙边缘区域，轴向BY、BZ强度产生微小波动。

图7 T-形磁通集聚器磁通图

3 T-形磁通集聚器放大特性影响因素的分析

通过以上对T-形磁通集聚器磁场放大原理分析可知，磁通集聚器对外部磁场的放大倍数不仅与磁通集聚器的形状有关，还与它的材料磁特性有关，磁通集聚器形状又是由不同的参数比例构成的，因此需要研究磁通集聚器的磁导率、长宽之比、空气间隙和结构厚度对外部磁场放大倍数的影响。利用ANSYS软件针对T-形磁通集聚器放大特性影响因素进行仿真分析。

为了分析不同磁导率对磁通集聚器放大倍数的影响，按表1中的数值设定T-形磁通集聚器的尺寸参数。在仿真过程中，分别设置磁通集聚器相对磁导率μr为100、500、1 000、3 000、5 000、8 000、10 000，仿真结构如图8（a）所示。从图中可以看出，磁通集聚器放大倍数随材料的相对磁导率的增大而增大，在相对磁导率增大到一定值时，磁通集聚器放大倍数已趋于稳定，达到了饱和值。通过曲线拟合可知，磁通集聚器材料的相对磁导率与外部磁场的放大倍数呈非线性关系。仿真结果与磁场集聚放大理论分析相一致。在分析不同长宽之比l/do对磁通集聚器放大倍数的影响，根据表1中的结构尺寸参数，改变磁通集聚器的长度l来改变结构的长宽之比，分别设置磁通集聚器的长宽之比为0.1、0.125、0.25、0.5、1、2，其它参数不变，材料的相对磁导率为105，仿真结构如图8（b）所示。从图中可以看出，磁通集聚器长宽之比越大，外部磁场的放大倍数就越大。通过曲线拟合可知，磁通集聚器的轴向磁场放大倍数与结构长宽之比之间呈单调递增的变化关系。为了分析不同空气间隙宽度对磁通集聚器放大倍数的影响，根据表1中的结构尺寸参数，在其它条件不变的情况下，改变空气间隙的宽度lg仿真分析结构空气间隙宽度对外部磁场放大倍数的影响，分别设置空气间隙宽度为0.1 mm、0.5 mm、1 mm、2.4 mm、3.4 mm、4.4 mm，仿真结果如图8（c）所示。从图中可以看出，磁通集聚器的轴向磁场放大倍数随结构间隙长度的增大而减小。通过曲线拟合可知，磁通集聚器空气间隙宽度与外部磁场的放大倍数呈非线性关系。在分析厚度对磁通集聚器放大倍数的影响中，根据表1中的结构尺寸参数，在其它条件不变的情况下，改变结构厚度仿真研究磁通集聚器厚度对外部磁场放大倍数的影响，分别设置厚度尺寸为1.95 mm、3.25 mm、4.55 mm、5.85 mm、7.15 mm，仿真结果如图8（d）所示。从图中可以看出，不同厚度的磁通集聚结构磁场放大倍数没有明显的变化规律。

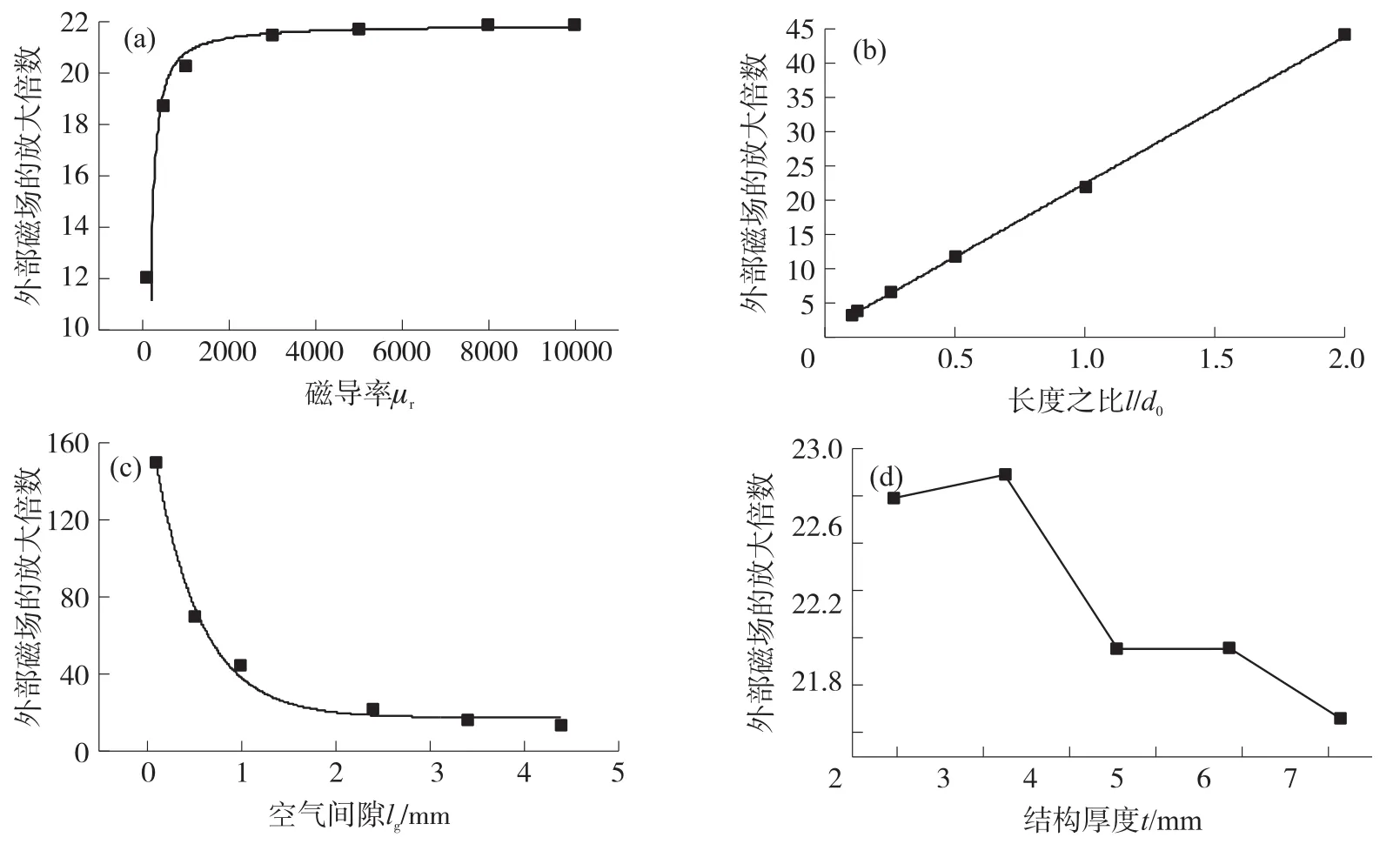
图8 磁通集聚器轴向磁场放大特性影响因素

4 试验测试

为了验证磁通集聚器轴向磁场放大特性，对磁通集聚器进行了弱磁场环境下的测试。根据制备要求的实际情况，利用线切割方法将软磁材料加工成参数尺寸如表1的T-形磁通集聚器结构，再进行高温退火处理，退火后得到T-形磁通集聚器如图9所示。

图9 退火后磁通集聚器示意图

在测试过程中，令亥姆霍兹线圈产生的环境磁场在±2.24×104nT范围内按正反行程方式进行往复变化，结构间隙内部三分量磁感应强度通过校准后的HMC1043三轴磁阻传感器进行测量。其中传感器z轴沿结构磁场放大轴向，x轴位于结构平面并与z轴正交，y轴垂直于结构平面。图10为带有T-形磁通集聚器及未加磁通集聚器磁传感器放大轴向测量数据对比图，从图中可以看出，磁通集聚器确实能够对环境周围磁场具有放大作用。T-形磁通集聚器轴向放大磁场三轴分量如图11所示。

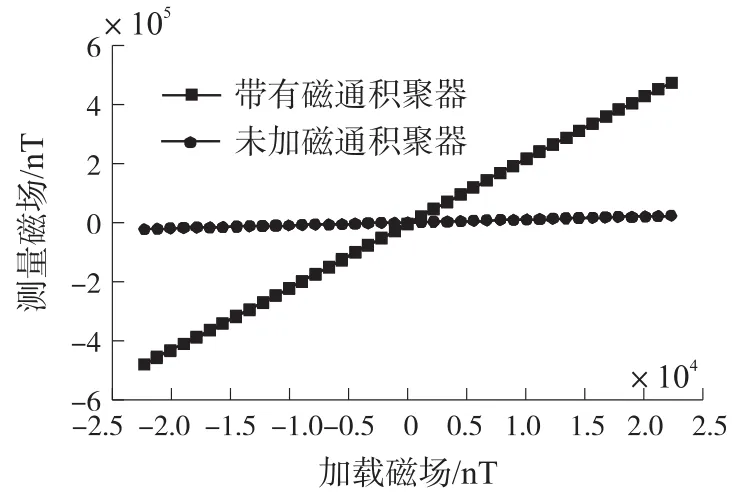
图10 T-形磁通集聚器与未加结构放大磁场z轴对比

图11 T-形磁通集聚器放大磁场三轴分量

从图11可以看出，x、y两轴上的磁场强度存在微笑波动，这是由磁传感器安装误差引起的。曲线拟合得到磁通集聚器对外部磁场的放大倍数为21.8倍。通过以上分析可得，T-形磁通集聚器通过仿真和实验得到外部磁场放大倍数存在微小误差，这是由于仿真过程结构的网格划分及磁传感器测量安装都存在着一定的误差。因此，可以认为实验结果与ANSYS仿真的结果相一致。

为了验证不同长宽之比的磁通集聚器轴向磁场放大特性，在其它尺寸相同的情况下，针对总长度l为100 mm的T-形结构及总长度为50 mm结构进行测试并将测试数据进行对比，对比结果如图12所示，线性拟合得到总长度l为50 mm和100 mm结构的放大倍数分别为21.8、42。可以看出相比于T-形（50 mm）集聚结构，总长度100 mm的磁通集聚器的放大倍数接近T-形（50 mm）集聚结构轴向放大倍数的两倍，结果表明结构长宽之比越大，轴向磁场放大倍数越大。此试验结果与仿真的结果相一致。

图12 T-形（50 mm）结构及T-形（100 mm）结构放大磁场对比

为了验证不同空气间隙宽度的磁通集聚器轴向磁场放大特性，对间隙分别为2.4 mm、3.4 mm及4.4 mm的T形结构进行了测试，测试结果如图13所示，线性拟合得到相应的放大倍数分别为21.8、17.1、15.2，可以得到，磁通集聚器的轴向磁场放大倍数随结构间隙长度的增大而减小，试验结果与仿真的结果相一致。

图13 不同空气间隙加载磁场与测量磁场之间关系

为了验证不同厚度的磁通集聚器轴向磁场放大特性，对结构厚度分别为4.55 mm、5.85 mm、7.15 mmT-形磁通集聚结构进行了测试，测试结果如图14所示，线性拟合得到相应的放大倍数分别为21.8、22.3、19.5，可以看出不同厚度的磁通集聚结构磁场放大倍数没有明显的变化规律，可以得出磁通集聚结构厚度对其放大倍数基本没有影响。试验结果与仿真的结果相一致。

图14 不同厚度加载磁场与测量磁场之间关系

4 总结

在现阶段常用的微型磁传感器精度低，无法满足地磁场环境中弱磁场高灵敏度高精度的测量需求。通过一系列的仿真及实验验证证明了磁传感器外加上磁通集聚器能够用于提高磁测系统的灵敏度，能够在无源的条件下提高弱磁场测量的精度。仿真结构与试验结果之间存在微小的偏差，这是由于仿真过程中网格划分或软件内部计算存在的误差及试验存在的误差造成的，因此，可以认为仿真结果与试验结果相一致。可以通过选择性能更好的材料及改变磁通集聚器形状及尺寸大小来更好的提高磁传感器的性能。该研究结果能够为磁通集聚器结构设计及优化方面提供一定的参考价值。

［1］Mengchun P，Jiafei H.Magnetic flux vertial motion modulation for 1/fnoise reduction of magnetic tunnel junctions［J］.Sensors and Actuators A：Physical，2012，179：92-97.

［2］Deeter M N.Fiber-optic Faraday-effect magnetic-field sensor based on flux concentrators［J］.Appl Opt，1996，35（1）：154-7.

［3］Deeter M N.High sensitivity fiber-optic magnetic field sensors based on iron garnets［J］.1994，522.

［4］Isabel G.T，Juliana O.Soft Thin Films for Flux Concentrators［J］.ieee transactions on magnetics，2009，45（1）：168-171.

［5］Sun X，Jiang L，Pong P W T.Magnetic flux concentration at mi⁃crometer scale［J］.Microelectronic Engineering，2013，111：77-81.

［6］Schneider M，Castagnetti R，Allen M，et al.Integrated flux concen⁃trator improves CMOS magnetotransistors［C］.Proceedings of the Proc IEEE Microelectromechanical Syst Conf，1995：151-6.

［7］Simon B，Oliver P.Magnetic field amplification by slender cuboidshaped magnetic concentrators with a single gap［J］.Sensors and Actuators A：Physical，2010，157（1）：135-139.

［9］Sansheng W，Tongfu H.research on a superconducting magnetic flux concentrator for a GMI-Based mixed sensor［J］.the ieee coun⁃cil on superconductivity，2014，24（5）.

［10］Xiaoguang Y，Hang L.A giant magneto resistive（GMR）effect based current sensor with a toroidal magnetic core as flux concen⁃trator and closed-loop configuration［J］.the ieee council on super⁃conductivity，2013，24（3）.

［11］Leroy p，Coillot c.Optimization of the shape of magnetic field con⁃centrators to improve the sensitivity of hall sensors［J］.Tm-tech⁃nisches messen，2006，73（6）：339-349.

［12］Popovic R S，Blanchard H.Hall sensors with integrated magnetic flux concentrators［C］.Hartung-Gorre Verlag，1999.

［13］Drljaca P M，Vincent F，Besse P A，et al.Design of planar magnet⁃ic concentrators for high sensitivity Hall device［J］.sensors and Actuators A，2002，97（98）：10-14.