基于TIDW的木材内部缺陷三维应力波成像方法*

陈方翔，冯海林，杜晓晨，方益明，翁 翔

（1.浙江农林大学信息工程学院，杭州311300；2.浙江省林业智能监测与信息技术研究重点实验室，杭州311300）

应力波断层成像技术在木材无损检测中得到了广泛应用。Ross等［1］最早利用应力波检测技术对红橡树腐朽区域进行检测。通过应力波成像软件观察所获得的图像能得到木材内部腐朽位置、面积和腐朽程度［2］。如王立海等［3］利用应力波与X射线二维CT图像的结合诊断能高效准确地确定原木内部腐朽区域；戚大伟等［4］对X射线图进行滤波、锐化，从而使得木材内部缺陷的细节更加明显；Wang等［5］利用应力波成像技术采用8个传感器对原木进行初期腐朽检测，实验结果表明该技术检测木材内部缺陷准确率达到62%，其中有8.5%的健康木材被误检为腐朽材。梁善庆等［6］通过应力波断层成像技术获取木材二维断层图像，通过断层图像获取木材内部缺陷的大小、形状等信息。杨学春等［7］利用应力波法对原木内部腐朽检测的相关内容进行研究，结果表明应力波测试仪能得到原木内部腐朽基本形状的二维图像，并判断不同树种内部的严重腐朽情况。

这些研究大部分都是利用现有的商业化成像软件进行二维成像应用研究，对应力波成像算法本身的研究还比较少见。冯海林等［8］提出一种图像重建算法，利用周围点值估计未知网格点的速度值，测试结果证明了该方法的可行性。Choi等［9］利用基于模型的损伤检测算法来定位缺陷位置及腐朽程度。木材三维应力波成像对算法本身的研究也较少，研究人员常常利用无损检测技术获取木材二维断层图进行三维研究。Brancheriau等［10］利用超声波成像技术，获取木材内部结构。王在山等［11］利用线性插值法对木材CT图像进行三维重建，从而提高木材利用效率。

反距离加权算法（Inverse Distance Weighted）最早用于气象和地质成像研究。刘广明等［12］利用光谱指数法与IDW法对三维土壤盐分空间变异特征进行了解析与评价，提升了区域土壤盐分的三维预测精度。Wang等［13］利用IDW方法获取长江及黄河流域气象数据，得到人类活动与气象的关系。陈冬花等［14］分别利用IDW法与Kringing法分析气温与海拔的关系，实验结果表明在低温环境下IDW模型模拟效果比Kringing模型略好。该算法根据空间分布规律对未知区域进行推演，具有较好的实验测试效果，并且其运算速度快、使用范围广、计算时所需存储空间小等特征，在气象、地理成像研究中较为常见。

将IDW算法应用于木材内部缺陷应力波三维成像会存在如下问题：①预估点的计算结果与邻域内所有已知点均有关，增加了算法复杂性；②预估点的计算结果与邻域内所有已知点之间的距离有关，忽视了插值点的空间结构性。因此，本文提出了一种TIDW（Top-kInverse Distance Weighted）算法，该算法将预估点邻域关系扩展到三维空间，增加预估点的搜索半径，找出邻域内与其距离小于搜索半径的所有已知点，引入Top-k查询，查找搜索半径内与预估点影响最大的k个已知点，从而计算得到预估点的值并进行应力波三维成像。利用TIDW算法与IDW算法对样本1至样本5进行三维应力波成像实验对比，结果表明TIDW成像算法具有更高的成像精度和检测准确率。

1 反距离加权算法

空间插值是一种利用已知点属性求得未知点属性的方法，通过空间中已知点与未知点的空间结构关系，从而计算得出未知区域中点的属性。

反距离加权算法是空间插值方法之一，常用于地理空间插值［15］。该方法利用预估点与已知点之间的距离为权重，离预估点越近的已知点权重越大，其权重大小与距离成反比。设空间预估点为pi（xi，yi）（i=1，2，3，…，n），其邻域内有已知点qi（xi，yi）（i=1，2，3，…，n），其中Zqi为邻域内已知点的属性值。待预估点Zpi属性值是通过待预估点邻域内已知点qi（xi，yi）的属性值Zqi加权平均值计算得出，其权的大小与待插点和邻域内点之间的距离di有关，是一种与距离的倒数成反比关系的插值方法。其基本公式为［16］：

其中Zpi为待预估点的估算值，Zi为邻域内第i个已知点的属性值，di为第i个已知点与待预估点之间的距离，n为参与插值计算邻域内已知点的个数。为权重系数，m越大则说明越靠近预估点的已知点对插值结果的影响越大。

2 TIDW成像算法

本文改进了IDW算法，提出了TIDW（Top-kIn⁃verse Distance Weighted）的应力波成像算法，对预估点与其邻域内已知点的空间结构性进行了优化，增加了预估点的搜索半径，引入Top-k查询技术，提高了预估点的计算精度。

2.1 邻域空间扩展方法

算法根据木材周围传感器采集到的应力波传播速度数据，得到邻域内已知点的速度集，并通过已知点数据集，计算得到预估点的属性。在计算预估点属性时需对其邻域内已知点进行筛选，本文中的筛选方法参考了空间定位［17］和方位搜索法，其中方位搜索法一般包括四方搜索、六方搜索、八方搜索等，方位的划分越多，则选择的参估点越多。四方搜索法，是根据预估点的横、纵坐标把平面分成四个象限，在每一个象限中查找与预估点距离最近的已知样本点。文中将二维空间中的四方搜索法扩展至三维空间中，当预估点位置确定后，利用其搜索半径查找相关已知点。若空间区域为N，邻域内的已知点X属于N，预估点根据搜索半径筛选X中的已知点。预估点计算方法如下：

①设预估点pi（xi，yi）周围8个邻域空间内存在个已知点qi（xi，yi）（i=1，2，…，M，M＜X），且qi的属性为Zqi。

②每个邻域空间中qi的选取应满足搜索半径r，r满足r＜R（R为木材的半径），r的取值应保证预估点pi（xi，yi）在空间邻域内存在已知点qi与之相关，并设阈值δ，当搜索到已知点的数目小于该阈值δ时，可扩大搜索半径，直到搜索到的已知点数达到该阈值为止。

③令λpi表示预估点pi（xi，yi）到其邻域内有关点的权重，则λpi可以表示为：

其中，表示点pi（xi，yi）和qi（xi，yi）之间的距离倒数，m为适合的常数，通常m=1。可将式（1）转化为：

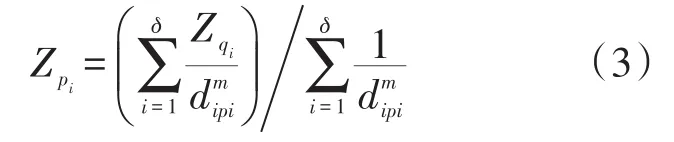
2.2 基于Top-k查询方法

Top-k查询技术主要用于查询大量数据中相关性最大的k个结果［18-19］，TIDW算法利用Top-k查询技术，找出在预估点邻域范围内与其影响最大的k个已知点及其属性。Top-k查询定义如下：给定M个元组的集合T，每个元组具有m′=（u1，u2，…，um）个属性，将集合T，存储为列文件的集合S={S1，…，Sm}，每个列文件为二元组合Si（rid，ui），其中rid表示对象的标示符，ui表示对象在属性处的属性值。每个列文件的存储方式为各元组的属性值的单调非增序列。定义F为m′个属性的评分函数，其式如下［20］：

λi是评分函数定义在属性值ui上的权重。通常，F是单调函数，即 ∀a1,∀a2∈T，如果对所有1≤i≤m′，a1u1≤a2u2，那么。利用Top-k查询技术查询集合T，中各元组的k个子集，通过读取m列已经降序排列的列文件集合S，顺序读取序列中，当元组rid出现时，随机读的方式在另外一个m-1个列文件获取其他属性值，然后计算他们的评分值，如果这个值是目前见过最大的k个，用优先队列维护k个元组及其相关信息。对每一列序列，设其当前读取位置ui，设阈值τ=F（u1，u2，…，um），当优先队列里k个元组分数值的最小值不小于τ时，查询结束。将式（3）变形如下：

Zqi为已知点的属性值，λpi为定义在属性值上的权重，为最终属性值。根据式（4），将式（5）变形如下：

Zqi为已知点的属性值，为定义在属性值上的权重，F(pi)为评分函数。

2.3 TIDW算法成像步骤

步骤1：输入传感器采集到的应力波速度数据；

步骤2：输入传感器坐标X（x，y，z），通过采集的时间矩阵Tm×n，计算出线速度Vm×n矩阵；

步骤3：设预估点X为2 000，计算出邻域内已知点集M′，计算权重 λpi；

步骤4：设定r与阈值δ根据式（2）计算权重，保存为序列形式；

步骤5：利用式（5）与已知点集M′求Zpi，令i=1，转步骤③；

步骤6：令 λi=λpi；带入式（6）；

步骤8：根据式（6）中的属性值F（pi），将预估点根据不同属性值进行颜色赋值，并三维可视化。

3 实验分析与结果

本实验采用项目组自主研发的便携式木材断层成像设备，在对木材进行检测时，需要在被测木材的不同高度处随机安装传感器，每次使用12个传感器进行数据采集，实验时依次敲击各个传感器，对同一样本需进行2次数据采集，共采集24组数据，将数据用于三维成像分析。图1为敲击12个传感器采集样本实验数据图。

图1 成像设备及检测方式

3.1 实验材料与方法

本实验样本编号、样本种类、样本周长、样本测量高度、样本含水率等信息如表1所示。

表1 实验样本基本信息

本文实验采用意大利Klortner公司生产的KT-R重锤式木材测湿仪来测量含水率。在样本缺陷内注入适量的水，直到水量达到测量高度时停止，取出缺陷内水并将其倒入量杯测量缺陷内水的体积V′得到样本缺陷体积，样本体积V是由样本横截面的面积乘以测量高度计算得到，公式如下：

图2为样本1至样本6的实物图，本实验利用人工挖凿空洞与自然腐朽的孔洞进行测试效果对比。其中样本1、3、6中的孔洞为人工挖凿，用于模拟真实腐朽情况；样本2、4、5中的孔洞为自然腐朽。

图2 6个实验样本木桩

3.2 IDW算法与TIDW算法成像结果对比

将两种算法分别对不同缺陷类型样本进行成像实验对比，实验结果如表2至表6所示。成像结果中以深色点组成的区域来模拟样本中实际腐朽的区域，浅色点组成的区域来模拟样本中健康的区域。

表2为对缺陷相对规则并且缺陷为工人挖凿的样本进行二维成像测试，由测试结果可知，IDW算法的成像结果并不能显示缺陷位置，而TIDW算法的成像效果较好，并能反映出缺陷的基本位置与缺陷情况。

表3为对样本1-2进行三维成像测试。样本缺陷体积相对均匀，并由表中实验结果可知，利用IDW算法的成像结果并不能显示缺陷的腐朽程度，而TIDW算法三维成像效果较好，能反映出缺陷的位置与缺陷的腐朽程度。

表4为对缺陷不规则并且为自然腐朽的样本进行二维成像测试。由测试结果可知，IDW算法成像结果并不能显示缺陷位置，而TIDW算具有较好的成像效果，并能反映出缺陷的基本位置与缺陷情况。

表5为对样本3至样本5进行三维成像实验，样本3和样本4的缺陷体积相对均匀，而样本5的缺陷不均匀。由表中实验结果可知，利用IDW算法成像效果并不能显示缺陷的腐朽程度，而TIDW算法的三维成像效好，并能反映出缺陷的位置与腐朽程度。

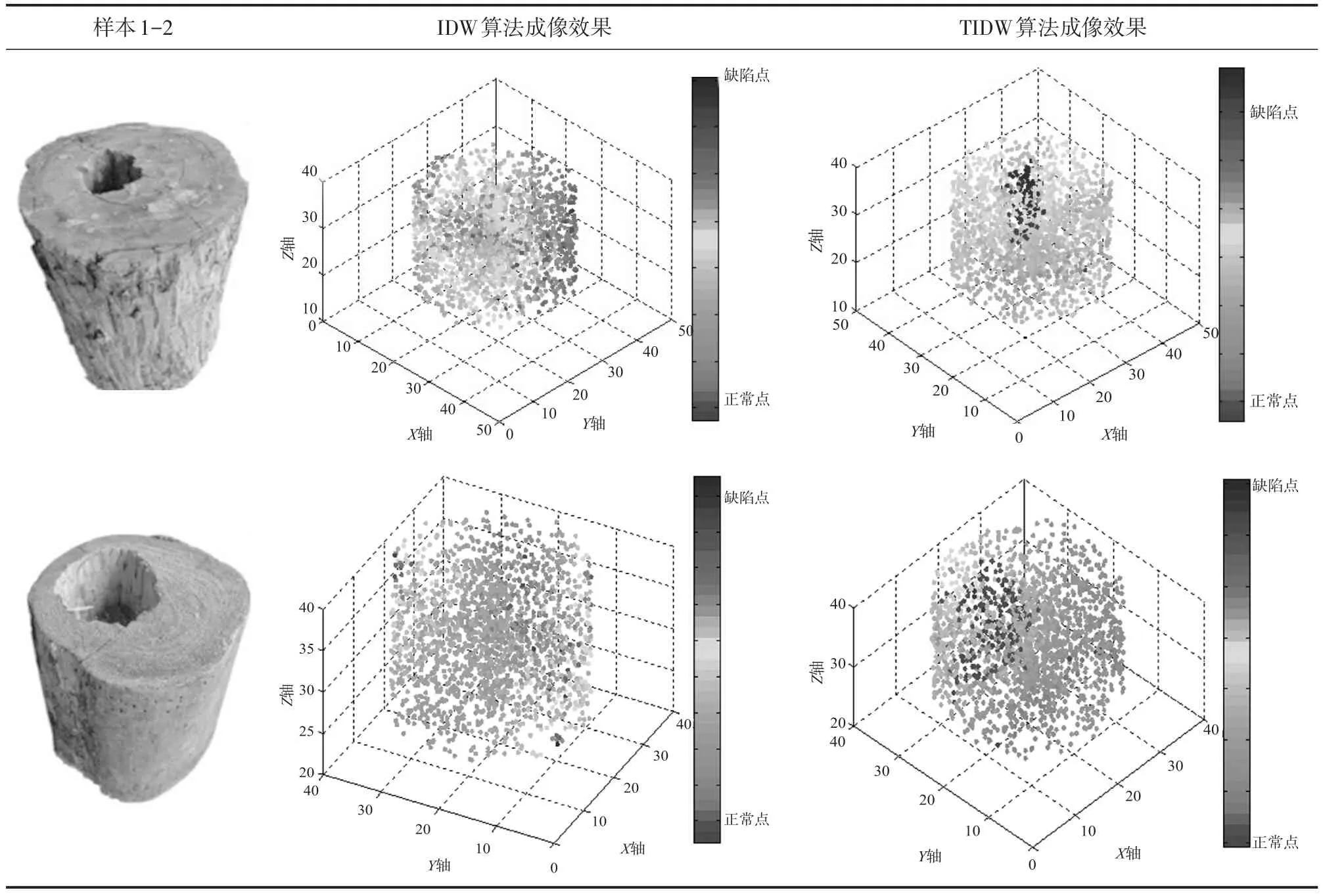
表2 缺陷规则的样本二维测试结果

表3 缺陷规则的样本三维测试结果

表4 缺陷不规则的样本二维测试结果

表6为对缺陷相对规则并且存在2个工挖凿的空洞样本进行二维与三维成像测试。由测试结果可知，IDW算法成像结果并不能显示缺陷位置与缺陷腐朽程度，而TIDW算法成像效果相对较好，能反映出缺陷的基本位置，但不能很好的反映出缺陷的腐朽程度。

3.3 成像结果分析

表7中显示缺陷的实测量体积、算法计算得到的缺陷体积以及相对误差，用于验证检测结果的正确性。通过计算图中红色缺陷部分点的比率乘以实测样本体积，可得到缺陷部分体积，如下：

其中Vi为通过算法计算得到缺陷部分的体积，V为对应样本体积，n′为缺陷点个数，X为插值点总数。

V1为利用IDW算法计算所得体积，V2为利用TIDW算法计算所得体积。Dt1为IDW算法计算得到的缺陷体积与实测缺陷体积的相对误差，Dt2为TIDW算法计算得到的缺陷体积与实测缺陷体积的相对误差，其公式如下：

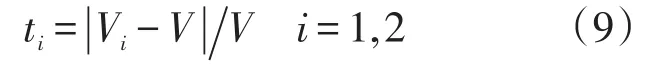
表5 缺陷不规则的样本三维测试结果

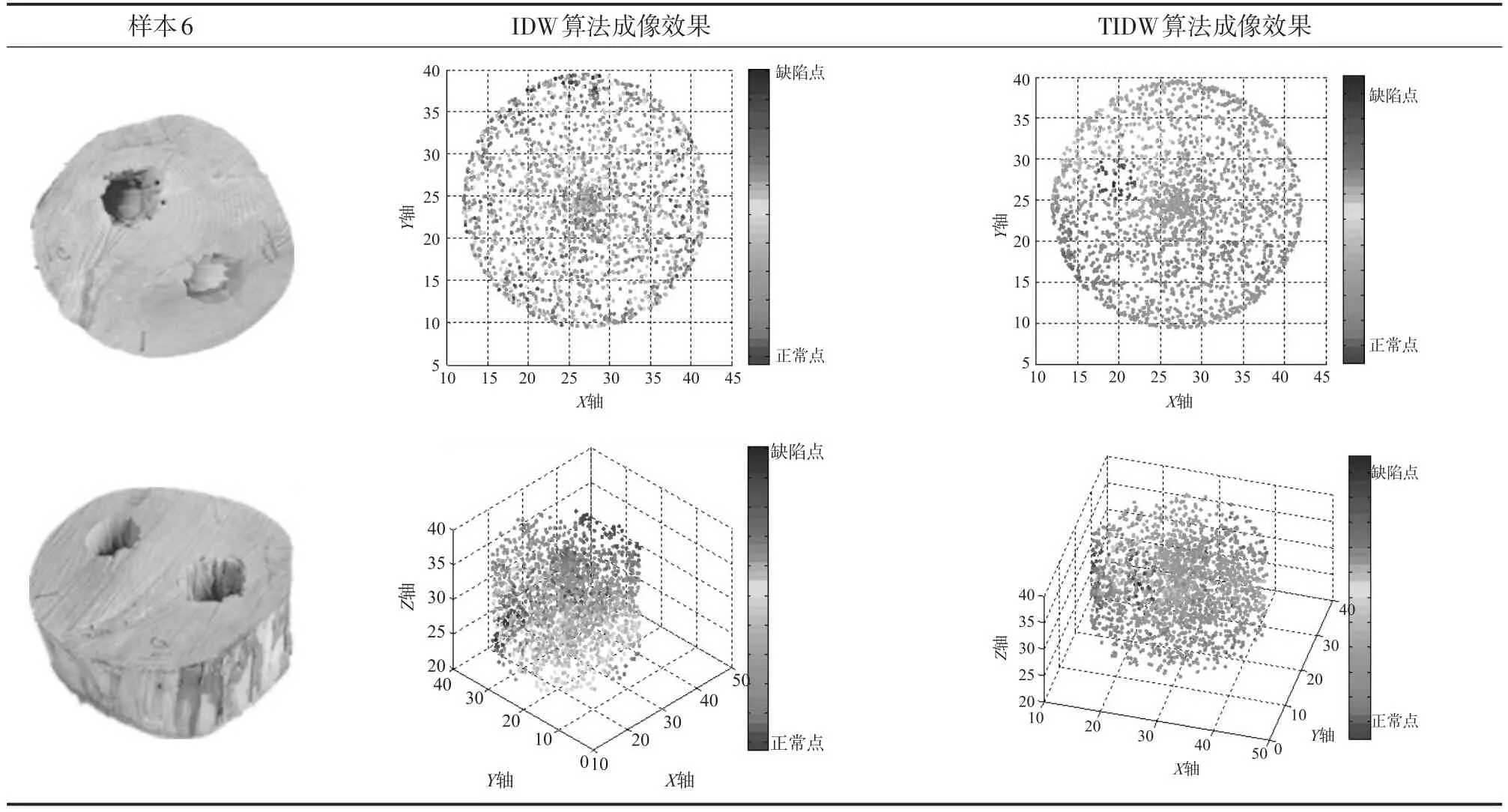
表6 样本中存在多个缺陷的测试结果

表7 样本缺陷检测结果

本文中1至6号实验样本的实测缺陷体积、计算得到缺陷体积及相对误差信息如表7所示。其中相对误差Dt1的范围在14.07%～422.2%之间，相对误差Dt2的范围在0.18%～52.56%之间，样本1至样本5的相对误差Dt2小于相对误差Dt1，并且相对误差Dt2在16.1%以内，而样本6中的相对误差Dt2大于相对误差Dt1。实验结果显示样本1，2，3，4的相对误差Dt2在10%以内，表明利用TIDW算法成像的精度较高；相对误差，说明利用IDW算法成像效果并不理想，与样本实际缺陷体积有较大误差。样本5的相对误差Dt2为16.1%，其误差偏大的原因可能是由于样本5的上下端腐朽程度相差较大，腐朽不均匀，使得TIDW算法成像结果与实际情况存在一定误差，即利用算法计算所得的缺陷体积与实际缺陷体积有较大误差；样本6的相对误差Dt1为14.07%，相对误差Dt1小于相对误差Dt2，但由表6中实验图像结果可知，IDW算法成像结果中的缺陷位置与实际缺陷位置不同，缺陷的腐朽程度与实际样本的缺陷腐朽程度也不同；样本6的相对误差Dt2为52.56%，其原因可能是样本中存在2个人工开凿的孔洞，利用TIDW算法对此类样本进行成像时会存在较大误差，并结合由表6中成像结果可知，TIDW算法成像中的缺陷位置基本符合实际缺陷位置，但其腐朽程度与实际缺陷腐朽程度不同，因此两种算法对此类样本成像的准确率都不高。由样本1至样本6的检测结果可知，利用IDW算法检测样本中缺陷体积，其平均检测准确率仅为38.26%，而利用TIDW算法检测样本中缺陷体积，其平均检测准确率为85.24%。

4 结论

本文提出了一种基于TIDW的木材内部缺陷三维应力波成像方法，应用于应力波木材无损检测，并对木材内部缺陷进行三维成像研究。通过与IDW算法成像结果比较，该算法无论从定性还是定量上都能更好反映木材内部腐朽情况，具有较高的成像精度。利用传感器采集木材周围应力波传播速度，通过对不同样本缺陷情况进行实验，验证了该算法对木材内部缺陷三维成像的可行性。检测单个空洞的缺陷样本，算法成像准确率可达到85.24%以上，而针对多孔洞的样本实验检测准确率不高，能基本反映样本缺陷位置，但缺陷体积计算有一定误差，需要进一步研究。

［1］Ross R J，Ward J C，Tenwolde A.Identifying bacterially infected oak by stress wave nondestructive evaluation［J］.USDA Forest Service，Forest Products Laboratory，1962（30）：277-281.

［2］Gilbert A E，Smiley E T.Picus Sonic Tomography for the quantifi⁃cation of decay in white oak（Quercus alba）and Hickory（Carya spp.）［J］.Journal of Arboriculture，2004，30（5）：277-280.

［3］王立海，孙天用.基于应力波与X射线二维CT图像原木内部腐朽无损检测［J］.森林工程，2011，27（6）：26-29.

［4］戚大伟.木材无损检测图像处理系统的研究［J］.林业科学，2001，37（6）：92-96.

［5］Wang X P，Wiedenbeck J，Ross R J，et al.Nondestructive Evalua⁃tion of Incipient Decay in Hardwood Logs［D］.Gen.Tech.Rep.FPL-GTR-162.Madison，WI：U.S.Department of Agriculture，For⁃est Service，Forest Products Laboratory，2005.

［6］梁善庆，傅峰，胡娜娜，等.三种应力波断层成像诊断木材内部缺陷［A］.第二届中国林业学术大会，S11木材及生物质资源高效增值利用与木材安全论文集［C］.北京：中国林学会，2009，457-462.

［7］杨学春，王立海.红松木材结构缺陷对应力波传播参数的影响［J］.东北林业大学学报，2005，33（1）：30-31.

［8］Feng H L，Li G H，Fu S，et al.Tomographic image reconstruction using an interpolation method for tree decay detection［J］.Biore⁃sources，2014，9（2）：3248-3263.

［9］Choi F C，Li J，Samali B，et al.Application of modal-based dam⁃age-detection method to locate and evaluate damage in timber beams［J］.Journal of Wood Science，2007，53（5）：394-400.

［10］Brancheriau L，Saadat-Nia M A，Gallet P，et al.Ultrasonic Imag⁃ing of Reaction Wood in Standing Trees［J］.Acoustical Imaging，2012，31（3）：399-411.

［11］王在山，戚大伟.木材CT图像的三维重构［J］.森林工程，2014，30（6）：38-40.

［12］刘广明，吴亚坤，杨劲松等.基于光谱指数的区域土壤盐分三维空间变异研究［J］.光谱学与光谱分析，2013，33（10）：2758-2761.

［13］Wang Y，Ding Y J，Ye B s，et al.Contributions of climate and hu⁃man activities to changes in runoff of the Yellow and Yangtze riv⁃ers from 1950 to 2008［J］.Science China Earth Science，2013，56（8）：1398-1412.

［14］SONG J J，KWON S，LEE G W.Incorporation of parameter uncer⁃tainty into spatial interpolation using Bayesian trans-Gaussian kriging［J］.Advances in Atmospheric Sciences，2015，32（3）：413-423.

［15］Song J J，KWON S，LEE G W.Incorporation of parameter uncer⁃tainty into spatial interpolation using Bayesian trans-Gaussian kriging［J］.Advances in Atmospheric Sciences，2015，32（3）：413-423.

［16］范玉洁，余新晓，张红霞，等.降雨资料Kriging与IDW插值对比分析-以漓江流域为例［J］.水文，2014，34（6）：61-65.

［17］张晋升，李一博，王伟魁，等.基于TFDA的有限空间多目标声定位方法［J］.传感技术学报，2013，26（11）：1508-1512.

［18］聂云峰，王长胜，陈崇毅.一种空间查询高效的无线传感网络路由协议［J］.传感技术学报，2015，28（5）：745-751.

［19］郑瑾，贾维嘉，王国军.无线传感器网络中基于数据分布表的Top-k查询协议［J］.传感技术学报，2010，23（9）：1340-1346.

［20］Shaikh S A，Kitagawa H.Top-koutlier detection from uncertain data［J］.International Journal of Automation and Computing，2014，11（2）：128-142.