基于玻尔兹曼的微机械陀螺温度误差补偿*

王增跃 ，李孟委 ，刘国文

（1.中北大学电子测试技术国家级重点实验室，太原030051，2.北京航天控制仪器研究所，北京100076 3.中北大学微系统集成研究中心，太原030051）

作为导航和姿态测量系统的核心器件，微机械陀螺因重轻、成本低、体积小、可靠性高等优点，已应用于民用车辆导航和军用机载导航、稳瞄、光电吊舱等系统中，有取代传统陀螺仪的趋势。微机械陀螺一般由单晶硅材料经光刻和刻蚀工艺制造而成［1］，硅材料是一种热敏材料，应用环境温度变化以及微机械陀螺长时间工作自身发热都会对零偏和标度因子产生较大影响。因此，大部分微机械陀螺还无法应用于高精度的姿态测量与惯性导航系统中［2-5］。在短时间内通过工艺改善来降低温度影响，提升微机械陀螺精度，难度较大，而通过实验数据分析，建立温度与零偏、标度因子的数学模型，并进行温度误差补偿，以提高微机械陀螺的应用精度是目前常用的途径。关于微机械陀螺温度特性分析与误差补偿，国内外已经进行大量深入的研究：文献［6］Abdel-Hamid通过对不同温度点下MEMS陀螺零偏特性的研究，验证了零偏输出特性的决定误差因素是环境温度的变化；文献［7］Aggarwal等人使用简单线性拟合的方法得到温度与MEMS惯性器件零偏之间的关系，经过补偿提高了导惯性导航的精度，但单一线性拟合不能达到较好的温度补偿效果，补偿后端精度仅为1 °/s～3 °/s；文献［8］中，使用混合线性回归的方法，对MEMS陀螺的输出进行补偿，使得补偿后的均值可以减小1～2个数量级，但运算过程相对复杂；文献［9］中，提出一种互相关分析快速温度标定的方法，与传统方法相比，节省大量时间，并且保证了模型的准确性，但其计算过程相对繁琐，可移植性差；文献［10］为了使得MEMS陀螺在一定温度区间进行分段拟合，但在增加计算量的基础上，并未达到较好的温度补偿效果。本文依托国家级重点实验室，通过高精度三轴温控转台研究微机械陀螺仪在-20℃～60℃条件下，环境温度变化对陀螺仪零偏及标度因子的影响，通过数据分析建立温度误差模型，并采用玻尔兹曼曲线拟合方法并进行温度误差补偿，相比线性拟合温度补偿，其温度误差补偿效果明显。

1 微机械陀螺仪温度误差机理分析

微机械陀螺仪以硅和石英为主要材料，当环境温度发生变化时，硅作为热敏材料会发生尺寸的变化，同时发生变化的还有材料的弹性模量热膨胀系数内应力等；其中主要影响因子为材料弹性模量和尺寸的改变。尺寸大小发生的变化对微机械陀螺仪误差影响很小，而硅材料弹性模量的变化对微机械陀螺仪性能有较大影响［11-13］。系统刚度随着材料弹性模量的变化而发生变化，进一步改变陀螺仪的谐振频率，陀螺仪输出产生漂移，材料弹性模量随温度变化近似成线性关系，如式（1）所示：

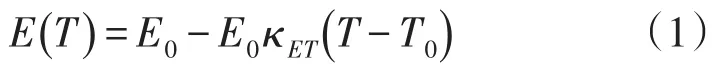
分析MEMS陀螺仪的工作机理，在温度T0附近的小范围内时，陀螺谐振频率与温度的关系可以线性近似的用式（2）表述：

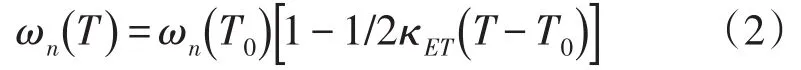
2 微机械陀螺仪温度实验

2.1 零偏温度实验

微机械陀螺仪温度实验装置如图1所示。将微机械陀螺仪静止固定在高精度三轴温控转台（转速精度：0。0001°/s）上，温度范围-20℃～60℃，按照应用需要，以10°C/小时的速度，分别进行升温和降温实验数据连续采集。温度范围内重复10次零偏试验。

2.2 角速率温度实验

微机械陀螺仪静止固定在三轴温控转台上，温度范围-20℃～60℃，按照应用需要，以10℃/h的速度，分别进行升温和降温实验数据连续采集。并在每个温度点进行角速率测试实验，即在每个温度点上，选取如下速率点（单位°/s）：0、±0.2、±0.5、±1、±2 、±5、±10、±25、±50、±75共19个速率点，进行恒温转速实验数据采集。温度范围内重复10次转速测量试验。

图1 高精度温控转台实验

3 零偏温度数据分析与补偿

10组试验数据变化趋势一致，以其中一组为例对原始数据进行分析，如图2所示，发现X轴陀螺和Y轴陀螺输出零偏受温度变化影响较大，且随温度的升高零偏值越大，最大偏移误差达到3°/s～4.4 °/s。

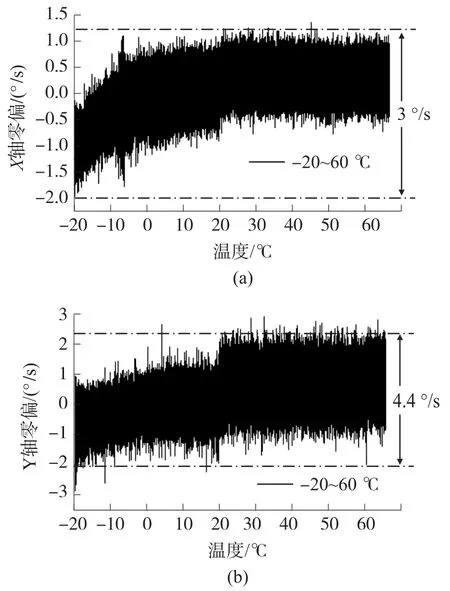
图2 X、Y轴陀螺零偏和温度关系

根据试验要求对每个温度点的X轴陀螺和Y轴陀螺采集的零偏数据求零偏均值，如表1所示。

表1 X、Y轴零偏均值——温度关系数据表

线性拟合：

玻尔兹曼曲线拟合：

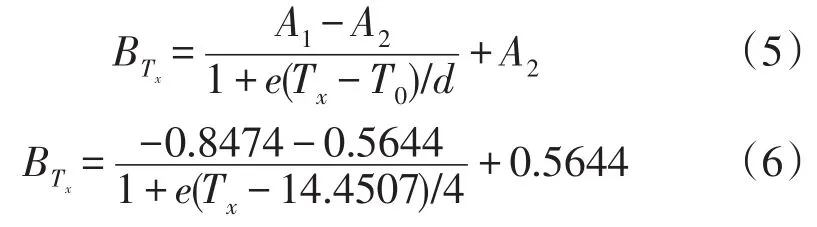
根据线性拟合公式和玻尔兹曼曲线拟合公式分别对微机械陀螺数据进行拟合，拟合公式如式（4）和式（6），X轴两种拟合效果对比如图3所示，根据拟合的数学模型进行误差补偿，补偿效果如图4。Y轴和X轴拟合效果相似，补偿效果如图5所示。

图3 零偏温度线性和玻尔兹曼拟合效果对比图

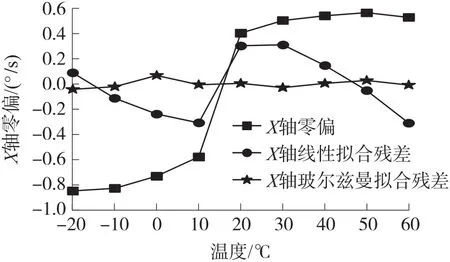
图4 X轴零偏温度线性补偿前后对比图

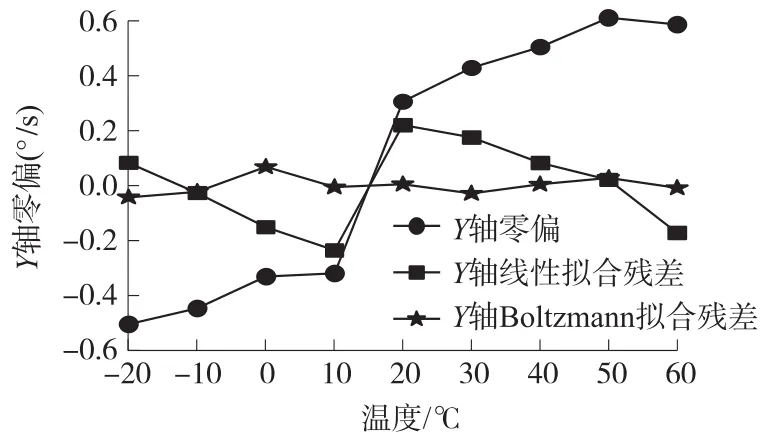
图5 Y轴零偏温度线性补偿前后对比图

4 标度因子温度误差分析与补偿

由于温度影响陀螺谐振频率导致的标度因子不稳定［16］，进一步影响微机械陀螺信号的输出，降低陀螺仪的姿态测量和导航精度因此，在实验数据基础上，分析陀螺仪输出，建立正确的温度误差模型并对陀螺仪输出进行补偿显得尤为重要。对温度实验数据进行分析，建立X轴、Y轴的温度标度因子数据表格，如表2所示，随温度变化趋势如图6所示。

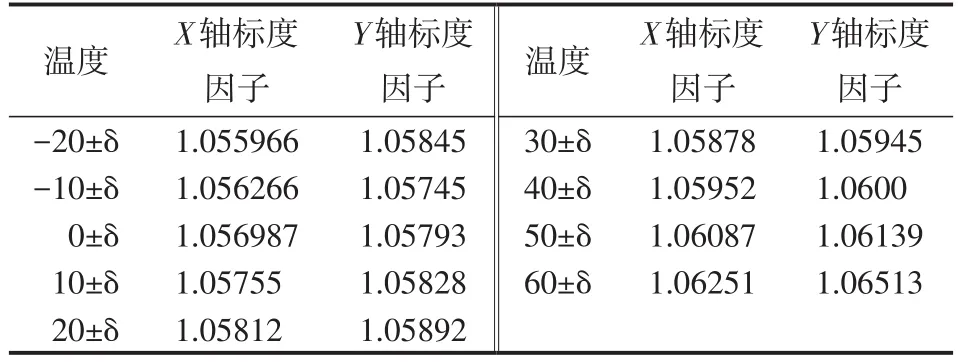
表2 X、Y轴标度因子——温度关系数据表

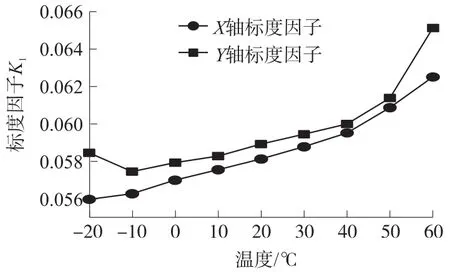
图6 X、Y轴陀螺的标度因子和温度的关系

根据式（3）和式（4）分别对标度因子进行线性和玻尔兹曼曲线拟合，得出拟合关系式（7）和式（8），拟合效果如图7所示。X轴数据和Y轴数据拟合原理和效果相似，以X轴数据为例进行拟合。

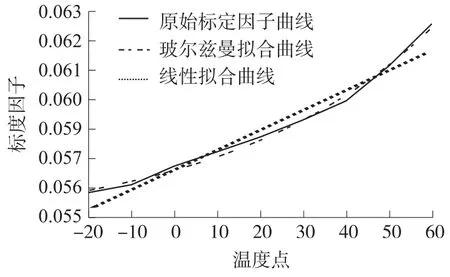
图7 陀螺的标度因子温度拟合效果对比关系

然后根据温度拟合关系式（3）和式（4），对输出角速率进行温度标度因子补偿，补偿效果如图8和图9所示。对比可知通过高精度转台测得补偿后的X和Y轴的加速率输出数据，玻尔兹曼曲线拟合方法要优于线性拟合。如图10、11所示，通过数据分析可得通过玻尔兹曼曲线拟合补偿后的角速率输出误差由原来的5°/s提高到补偿后的0.01°/s。

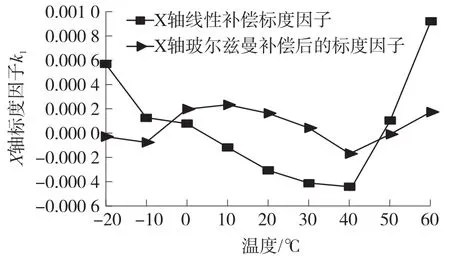
图8 X轴陀螺的标度因子温度补偿后对比关系

图9 Y轴陀螺的标度因子温度补偿后对比关系

图10 微机械陀螺标度因子补偿前后角速率输出图

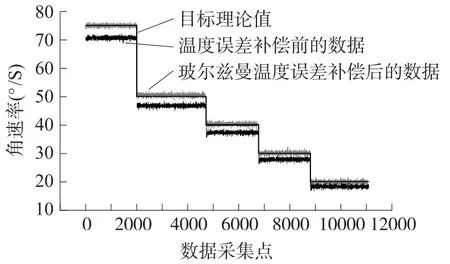
图11 微机械陀螺温度误差补偿前后角速率输出图

5 试验结果分析

综合温度对零偏和角速率输出的影响，分析玻尔兹曼曲线拟合对微机械陀螺的补偿效果：温度补偿前，一定温度范围内陀螺仪零偏最大误差为4.4°/s，如图2所示，标度因子最大误差为0.66%，如图6所示；补偿后该陀螺仪零偏最大误差降为0.2°/s，如图4、图5所示，标度因子最大误差0.003%，如图8、图9所示。总体而言，补偿后微机械陀螺仪精度提高1～2个数量级。

6 结束语

通过高精度温控转台测试实验，并结合微机械陀螺仪零偏输出、角速率输出与温度之间关系，使用最优拟合的方法，在一定温度范围内，对微机械陀螺仪温度误差建模；并通过温度误差模型进行温度误差补偿，减小了温度对微机械陀螺仪的影响，并验证玻尔兹曼误差模型的正确性与可实用性；该补偿方法可用于他项目微传感器误差的标定，有效的缩短时间和节约补偿成本。

［1］邱林茂，高文冀，李磊，等.导引头中MEMS陀螺漂移补偿算法研究［J］.火控雷达技术，2013，2（42)：1-2.

［2］Zhang Chong，Wu Qi-song，Yin Tao.A MEMS Gyroscope Read⁃out Circuit with Temperature Compensation［J］.Proceedings of the 2010 5th IEEE International Conference on Nano/MicroEngi⁃neered and Molecular Systems，2010：458-461.

［3］杨亮，苏岩，裘安萍，等.高品质因数微机械陀螺的温度自补偿［J］.光学精密工程，2013，11（21）2-3.

［4］李翊，刘炜，吴凌华，等.基于灰色模型的MEMS陀螺温度补偿［J］.海军航空工程学院学报，2015，2（30）1-2.

［5］秦伟，苑伟政，常洪龙，等.基于模糊逻辑的MEMS陀螺零漂温度补偿技术［J］.弹箭与制导学报，2011，31（6)：19-22.

［6］Abdel-Hamid W.Accuracy Enhancement of Integrate MEMSIMU/GPS Systems for Land Vehicular Navigation Applications［D］.PhdThesis，Department of Geomatics Engineering，Universi⁃ty of Calgary，Calgary，AB，Cananda，2005.

［7］Aggarwal P，Syed Z，EI-Sheimy N.Thermal Calibration of Low Cost MEMS Sensors for Land Vehicular Technology Conference［C］//VTC Spring，IEEE2008：2859-2863.

［8］陈维娜，曾庆化，李荣冰，等.微机械陀螺温度混合线性回归补偿方法［J］.中国惯性技术学报，2012，20（1)：99－103.

［9］罗兵，吴美平，尹文，等.微机械陀螺温度系数的快速标定方法［J］.传感技术学报，2011，23（10)：1445-1448.

［10］程龙，王寿荣，叶甫.硅微机械振动陀螺零偏温度补偿研究［J］.传感技术学报，2008，21（3)：483-485.

［11］陈怀，张嵘，周斌，等.微机械陀螺仪温度特性及补偿算法研究［J］.传感器技术，2004，23（10)：24-26.

［12］温祖强，钱峰.微机械陀螺温度特性及其补偿算法研究［J］.电子测量技术，2011，34（1)：51-54.

［13］苏中，李擎，李旷振，等.惯性技术［M］.北京：国防工业出版社，2010：38－40.

［14］陈湾湾，陈智刚，马林，等.MEMS微机械陀螺温度特性分析与建模［J］.传感器技术学报，2014，27（2）：1004-1699.

［15］赵旭，苏中，马晓飞，等.大温差应用环境下的MEMS陀螺零偏补偿研究［D］.现代传感技术学报，2012，8（25）：2-4.

［16］Fang Jiancheng，Li Jianli.Integrated Model and Compensation ofthe Rmal Errors of Silicon Microelectromechanical Gyroscope［C］//IEEE Transactions on Instrumentation and Measurement So⁃ciety，2009，9：2923-2930.