基于时间反转聚焦的声发射源定位算法*

李秋锋，陈建娟，何才厚，张 维，李帅辉，陈积乐

（1.南昌航空大学无损检测技术教育部重点实验室，南昌330063；2.江西省特种设备检验检测研究院鹰潭分院，江西鹰潭335000；3.南京大学近代声学教育部重点实验室，南京210093）

材料或结构在受力产生变形或断裂时，材料中局域源以弹性波的形式快速释放出应力应变能的物理现象称为声发射（AE），有时也称为应力波发射。声发射实质是一种力学现象，是应力波产生、传播和接收的过程，从声发射源到传感器接收都完全遵循弹性波传播理论［1］。随着声发射技术日益成熟，其在建筑、石油、生物医学、制造和军工等应用也越来越广泛［2-7］。

声发射检测技术中确定声发射源的具体位置是一个主要目的，其定位精度也是评价多通道声发射检测设备的一项重要指标。目前对于声发射源定位已经研究出很多方法，而对于突发型信号的声源定位方法可概括为两种：区域定位法和时差定位法。区域定位是一种快速、简便但是很粗略的定位方法，其具有传感器布置灵活，检测范围大的优点，但是检测到的声源位置表示在一个区域内；时差定位是根据声源所发出的信号到达同一组检测探头的不同时间差、声速及探头间距等参数经过几何关系计算出声源在该组检测探头检测范围内的具体位置，结果是一确定点，定位更加准确，因此目前大都采用时差定位法进行声发射源定位［8，9］。但是由于声发射源发出的信号是经过一段传输介质后到达传感器，传输过程中信号会发生形态变化和模式转化，因而实际传感器接收到的声波含有纵波、横波、表面波和板波等各种形式的声波，要在同一个门槛电压下各传感器接收信号中找出反映到达时间对应点是很困难的，可能测出的是不同模式波的时差，这样得到的时差就带有很大的误差，所以需要借助波形分析技术和信号处理方法，出现了许多模态分析和波形处理方法，在不同程度上提高了定位精度［10-12］。但是这些分析和处理方法都停留在对波形模态辨识和提取上，仍然存在一定误差。

时间反转是指将不同传感器接收到的声源发出信号，按时间历程的反向过程重新向介质追踪回去，即先到后发、后到先发，可有效实现声源信号重构的一种方法［13-15］。根据时间反转思想对声发射检测信号进行声源聚焦处理，就可以忽略波形模态的影响，使声源信号在空间上和时间上重新进行聚焦，使得信号同时同相到达聚焦点，其信号的能量也汇聚到聚焦点［16，17］。

1 声发射源定位方法

1.1 时间反转基本原理

时间反转是声互易性原理的应用之一，可不需要介质和传感器性质及结构的先验知识就可实现声波自适应聚焦，对声源或二次声源信号进行重构，准确检测声源位置。一个完整的信号传输系统包括传感器和传输介质，假设信号P（ω）经过传输介质被传感器接收到后，信号频响可表示为：

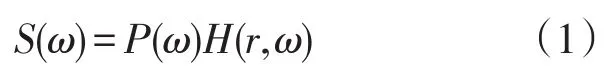
H（r，ω）为传输系统的通道传递函数。要获得接收信号S（ω）的时反信号实质就是对式（1）取复共轭，得到时反响应信号为X（ω）：

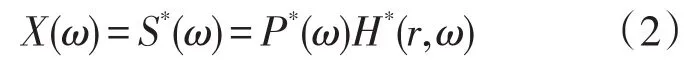
根据声波互易性原理，对于传输通道确定的结构，传感器和激励器位置可以互易，且具有相同的频率响应［18］。因此将时间反转后的信号X（ω）在对应的传感器上加载，波源处可得到信号则可表示为：

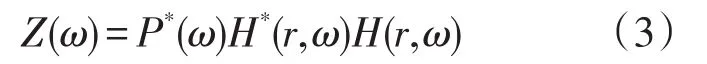
式中：P*（ω）为激励信号的频域共轭即时反信号；“H*（r，ω）H（r，ω）”为实、偶、正函数，其在时间零点的傅里叶逆变换将会同相叠加，形成主相关峰值，而当多个传感器一起按照此方法处理，通过累加后将使得声源处信号峰值显著增强，形成聚焦，这就是时间反转聚焦的基本原理。

1.2 声发射源信号增强机理

要将上述时间反转聚焦理论应用于声发射源定位上，首先要考虑声发射信号的传播特点。声发射检测是一种被动检测方法，没有外加激励信号，声发射信号是材料损伤处即声发射源直接发出，如图1所示，信号通过不同的传播路径被布置在周围的传感器接收到，进行时间反转处理，就需将接收到的信号反相加载到传感器上发出，将在声源处即可得到增强，形成聚焦。但是由于检测过程中监测范围内的声源位置是未知的，而声源对反转加载激励信号会产生散射，然后再被各传感器接收到，通过对反转加载后的接收信号进行处理也可以确定声源位置。

图1 声发射信号时间反转示意图

由于声发射信号本身就很微弱，如果反相加载后再次接收将产生大量干扰信号，这将会大大影响时间反转效果，所以在物理上实现接收信号的反相加载是很难实现的，因此提出一种通过数据处理的方式实现时间反转聚焦的方法。如图1所示，假设声发射源处因损伤发出声发射信号D（ω），图中四个传感器接收到的信号分别为Si（ω），（i=1，2，3…），令声源到各个传感器的传播通道传递函数为Hi（ω），（i=1，2，3…），那么各个传感器接收到的信号和声源有如下关系：

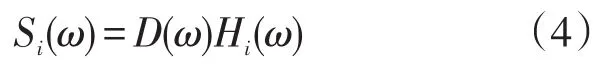
各个传感器接收到信号都是由声源发出，按照时间反转聚焦原理，将这些传感信号进行时间反转，损伤信号将于特定的时间在各自所对应的传感器上激发出去，使得激发出去的这些信号能够在声源处实现时间和空间上的聚焦。同时根据声波互易性原理，同一路径的传递函数是不变的，而时间反转处理实质是在频域里做共轭处理，根据上述条件推导出此时在声源处得到的信号Dr（ω）可由下式来表示：

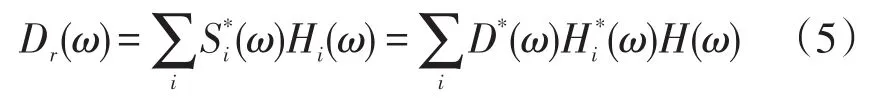
式中：“ΣHi（ω）Hi*（ω）”其实就是对声源信号的时间反转聚焦叠加，所以信号Dr（ω）的波峰幅值能够得到增强，并能够超过实际声源信号D（ω）中的最大波峰的幅值，因此该处理能够使得声源信号得到聚焦并增强。

实际监测过程中声源实际位置未知，因此Dr（ω）只是理论聚焦信号。考虑到声源处是一个损伤，会对时反加载信号产生散射而又被各个传感器接收到，假设各个传感器再次接收到的信号为Sij（ω），（i，j=1，2，3…），可用下式表示：

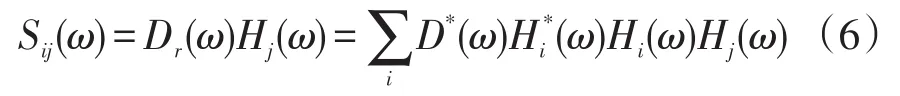
从式中可以发现“D*（ω）Hi*（ω）”实际为S*i（ω），即第i个传感器所接收到的声源信号的时反信号，而“Hi（ω）Hj（ω）”为从第i个传感器经过声源到达第j个传感器的传播路径的传递函数。按照以上处理过程，声源信号因聚焦而得到增强，而其他干扰信号的发生时间和位置不同，不能满足增强条件而被抑制，使得信噪比得到优化。

但是由于传播路径并不确定，传递函数无法获得，那么要实现对声源的时反聚焦，还是存在困难。为此将公式（6）做了改进，在方程两边同时乘以“D（ω）D（ω）”，并做一些组合后可以得到新的传感信号S’ij（ω）：

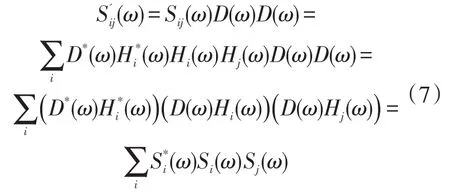
式中：三个乘积项都有很明确的物理意义，且都为已知信号，即为传感器直接接收的声源信号及其共轭处理信号。因此可以认为S’ij（ω）是信号“D*（ω）D（ω）D（ω）”作为声源信号的时间反转增强信号。而且由于“D*（ω）D（ω）D（ω）”与声源信号D（ω）具有相同的频域特征，因此也不会对传播速度等因素有影响。

1.3 声发射源成像原理

由公式（5）可知在聚焦时刻时反传感信号同时到达声源处并相互叠加，这个时刻声源成为能量最大的地方。根据声波传播原理，可以模拟计算出结构中各点处振动的能量和幅值。以能量为参数把计算结果用图像表示出了，则所成像中能量最大之处即为声源，从而实现对声源即损伤的成像检测。假设声源发出时刻为ts，该信号被最后一个传感器接收到的时刻为tm，令te＞tm，以te-ts为时间窗口用来分别截取所采集到的信号，并对截取后的信号进行时间反转得到信号fn（n＝1，2，…，N）。将时反后的信号的对应传感器上同时加载，则在声源处可得到重建聚焦信号，假定聚焦时刻为tf，其与声源发出的时间ts满足下面的关系：

按照声波传播原理，建立在聚焦时刻整个结构的波动图，图中的每个像素点都与结构相对应，每个像素点的像素值代表波动幅值，在聚焦时刻每个点上的波动幅值可结合下面两个公式来获得：

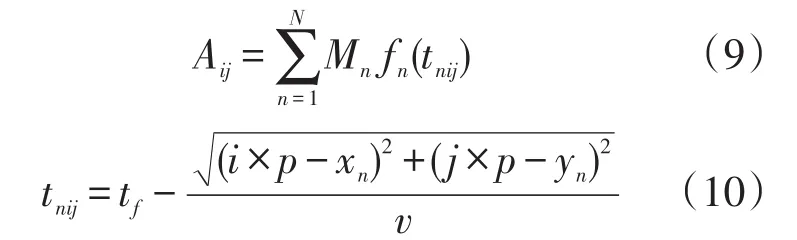
式中：v代表声波的传播速度，p代表图像的分辨率，N代表传感器接收到信号的总个数，Mn则是第n个传感器的补偿放大系数，这是因为每个传感器的性能以及接收的信号能量衰减都不一样。xn和yn则分别为第n个传感器所对应的坐标，Aij代表该点的幅值。

2 数值仿真研究

为了验证定位算法的有效性，采用有限元软件进行仿真研究。首先建立一个平面模型，模型尺寸为160 mm2×120 mm2，如图2所示，定义模型材料为钢板，密度为7.9×10-3g/mm3，弹性模量设置为210 GPa，泊松比设置为0.3，并对平面的边界设置了完全固定的边界条件。

在模型中布置了四个传感器分别为S1-S4，并根据突发型声发射信号设计了一个模拟声发射源D，位置为（-20，-4），具体分别情况如图3所示。根据突发性声发射信号特点，模拟了一个声发射信号如图4所示，其频率为0.5 MHz。将模拟信号在模型D处激发后，根据传感器离声源距离的不同分别采集到四个信号，如图5所示。

图2 平面钢板有限元模型

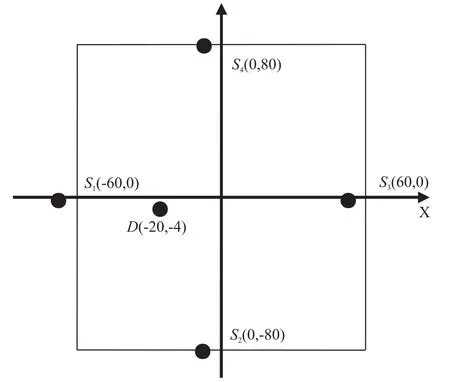
图3 模拟声发射源激励和传感器分布示意图

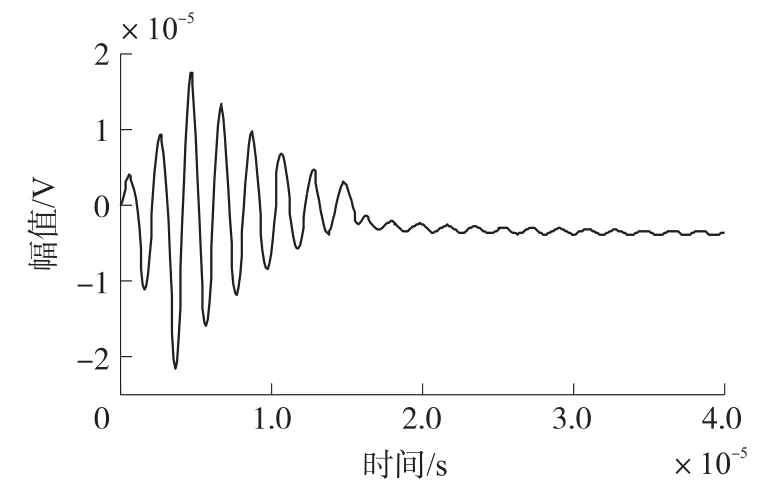
图4 模拟声发射信号波形图

利用公式（7）对各传感器信号进行增强处理，为了避免相位误差，信号的增强叠加采用的是包络线叠加。图6是对S1信号进行增强处理后的结果。从结果可以看出增强信号中声源信号的聚焦波峰突出，相对于图5中原传感信号，有用信号能量被明显放大，主峰明显，提高了信号信噪比。由于采用波形包络进行处理，图6中的增强信号波峰位置约为图4中波形的包络峰值与图5中传感器S1信号包络峰值间的时间差值，因此，在图6中约为75微秒。其它几个传感信号在经过增强处理后，也得到了相似的结果。

图5 四个传感器接收到的信号

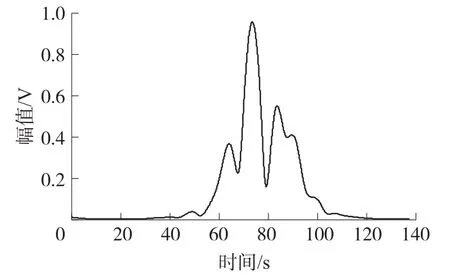
图6 增强处理后S1信号的包络图

利用四点圆弧定位方法求得聚焦时刻，即声源处接收各个传感器的时反信号后再次散射信号的时刻。按照上述条件和前文的成像步骤，建立聚焦成像重建区域，根据模型尺寸将区域划分成120×160个单元，每个单元1 mm，重建监测区域如图7所示。

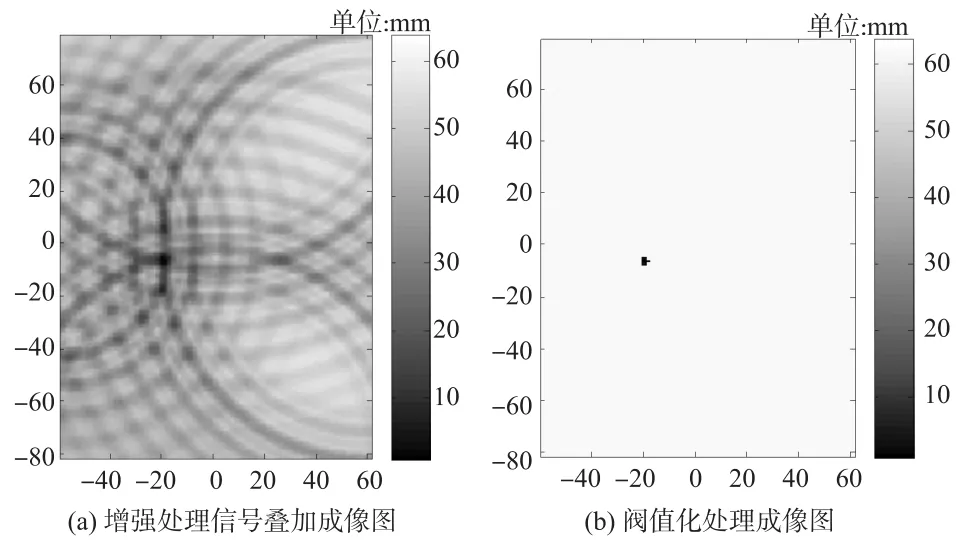
图7 增强处理信号成像图

在成像过程中，先将各增强信号分别成像，然后将四个成像结果叠加，结果如图7（a）所示。由于叠加成像图并不能突出显示声源位置，因此对其进行了阈值化处理，仅显示超过阈值的像素和像素值，阈值大小采用经验值80%，最终的声源成像结果如图7（b）所示，图中显示出声源位置为（-20，-6），以四个传感器间最大间距计算误差约为1.25%。而按照相同区域划分方法时，采用常规的时差定位法显示出声源位置为（-22，-8），误差约为2.8%。

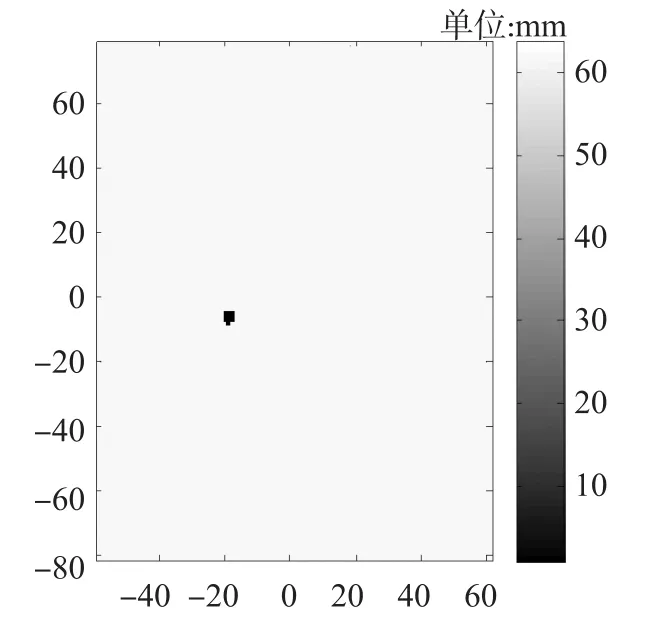
图8 时差定位法成像结果

3 结论

本文根据声发射检测中损伤准确定位的要求提出了一种基于时间反转聚焦的缺陷定位方法，通过结合声发射信号传播特点与时间反转理论，推导出声发射源信号增强方程，实现对声源的准确定位。通过有限元分析软件建立平面模型，模拟声发射源发出信号及其传播过程，根据增强方程对该声发射源进行定位，仿真结果表明该定位方法能准确找到声源位置，与常规时差定位法结果比较，能有效提高定位精度。

［1］耿荣生，景鹏.声发射技术在全尺寸飞机疲劳试验中的应用［J］.应用声学，2013，32（4）：246-251.

［2］Chang H，Han E H，Wang J Qet al.Acoustic emission，study of fa⁃tigue crack closure of Physical short and long cracks for alumi⁃num alloy LY12CZ.International Journal of Fatigue，2009，31：403-407.

［3］张涛，李一博，王伟魁等.声发射技术在罐底腐蚀检测中的应用与研究［J］.传感技术学报，2010，2（7）：1049-1052.

［4］杨班权，张坤，陈光南等.涂层断裂韧性的声发射辅助拉伸测量方法［J］.兵工学报，2008，29（4）：420-424.

［5］陈涛，刘丽川，方卫红等.油罐声发射检测信号数据库研究及应用［J］.应用声学，2013，32（2）：152-159.

［6］何培忠，段世梅，夏荣民等.超声激发生物组织声发射的原理及应用［J］.应用声学，2005，24（4）：259-264.

［7］卢超，丁鹏，陈振华等.不同拉伸速度下的碳布/环氧树脂复合材料声发射评价［J］.失效分析与预防，2012，7（1）：15-18.

［8］Jomdecha C et al.Study on source location using an acoustic emis⁃sion system for various corrosion types［J］.NDT&E International，2007，40：584-593.

［9］沈功田，耿荣生，刘时风.声发射源定位技术［J］.无损检测，2002，24（3）：114-118.

［10］单亚锋，孙朋，徐耀松等.基于PSO_SVM的煤岩声发射源定位预测［J］.传感技术学报，2013，26（3）：402-406.

［11］M.Surgeon，M.Wevers.One sensor Linear location of acoustic emission events using plate wave theories.［J］.Materials Science and Engineering，1999，254-261.

［12］金中薇，姜明顺，隋青美等.基于广义互相关时延估计算法的声发射定位技术［J］.传感技术学报，2013，26（11）：1513-1518.

［13］Mathias Fink，Time-Reversal of ultrasonic field-part I：basic prin⁃ciples［J］，IEEE Trans.Ultrason.Ferroelect，Freq.，Contr.，1992，39（5）：555-566.

［14］Francois Wu，Jean-Louis Thomas，Mathias Fink，Time Reversal of Ultrasonic Fields-Part II：Experimental Results［J］.IEEE Trans.Ultrason.Ferroelect，Freq.，Contr.，1992，39（5）：567-578.

［15］郑文军.复杂多散射环境下EM_TRM成像技术应用研究［J］.电子科技大学学报，2013，42（3）：365-368.

［16］王强，袁慎芳.复合材料板脱层损伤的时间反转成像监测［J］.复合材料学报，2009，26（3）：99-104.

［17］张海燕，孙修立，曹亚萍等.基于时间反转理论的聚焦Lamb波结构损伤成像［J］.物理学报，2010，59（10）：7111-7119.

［18］潘翔.基于时间反转处理的水声信号增强研究［J］.传感技术学报，2006，19（3）：847-850.