基于直觉模糊的编队舰空导弹类型优选模型*1



基于直觉模糊的编队舰空导弹类型优选模型*1

钟志通1，杨庆2，隋先辉1,张小东1

(1.海军大连舰艇学院，辽宁 大连116018; 2.南海舰队军训处，广东湛江510430)

摘要：从防空反导角度，对装备单型号舰空导弹水面舰艇进行战术编组的本质就是舰空导弹类型的选择。针对水面舰艇编队舰空导弹类型选择问题，建立了基于直觉模糊的编队舰空导弹类型优选模型，并结合实例检验了模型的有效性，对水面舰艇编队编成具有一定的指导意义。

关键词：直觉模糊；水面舰艇编队；舰空导弹类型

0引言

水面舰艇编队编成是指将不同类型水面舰艇有机组合，组成相对稳定的作战体系，使其具有与履行使命任务相适应的作战能力。而防空反导能力是编队作战能力的重要组成部分，编队编成时需根据需求选择装备不同类型舰空导弹的水面舰艇。对一型武器能力的评估通常采用总分评定法、功效系数法、指数法和模糊多指标决策法等综合评定方法，各方法均各有其优缺点、适用范围和使用条件。其中，总分评定法的局限性是缺少可比性，尤其是三档计分过于粗糙，不能客观准确地反映各评价指标间的差异，而功效系数法和指数法在处理定性指标时缺点比较明显。所以，本文选择直觉模糊多指标决策方法，研究水面舰艇编队舰空导弹类型优选问题。

1直觉模糊集概念引入

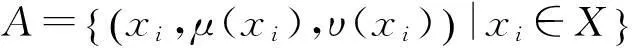
2基于直觉模糊集的优选模型[3-7]

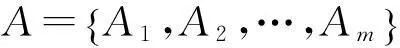
(1) 构建决策矩阵

假设由m个备选型号和n个评价指标所构成的决策矩阵为D=(dij)m×n，其中dij≥0。

(2) 规范化决策矩阵

为了消除不同物理量纲对决策结果的影响，需对决策矩阵D=(dij)m×n进行规范化处理，得到决策矩阵为G=(gij)m×n。规范化方法为

对于效益型指标：

gij=dij/maxdij，

(1)

对于成本型指标：

gij=mindij/dij，

(2)

式中：元素gij表示第i个型号Ai的第j个指标值的评价，gij越大对型号Ai的支持越高，越小对型号Ai的反对越高，位于中间的gij为支持Ai与否的不确定信息。其中，gij位于区间[0,υij]，(υij,μij)，[μij,1]时的评价分别为gij对型号Ai反对度、犹豫度和支持度的评价值。

(3) 确定υij，μij取值

υij，μij取值方法有多种，一般根据研究问题及其指标特性，结合本领域专家知识和经验进行确定。本文采用黄金分割思想，取黄金分割点υ0=0.382和μ0=0.618，即[0,0.382]，(0.382,0.618)和[0.618,1]，分别对应反对、犹豫和支持[8]。

(4) 进一步规范化处理；如果gij位[0,υ0]区间内，表示gij对型号Ai的反对度的评价，属于偏小型分布。而实际上决策矩阵内的所有元素gij都是规范化后得到的，均为偏大型分布，因此，需要对规范化矩阵G中的位于[0,υ0]区间内的元素gij进行进一步处理，得决策矩阵R=(rij)m×n，处理方法为

(3)

(5) 确定指标权重

(6) 对矩阵Y按行规范化处理，得到矩阵H=(hij)m×n，计算公式为

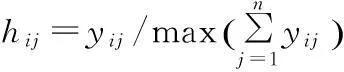
(4)

(7) 计算支持度和反对度

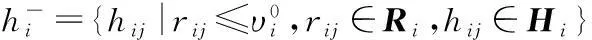
(8) 计算型号Ai模糊得分和精确度

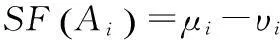
(5)

3舰空导弹型号优选指标

通常，水面舰艇编队是在航空兵掩护下遂行作战任务，其对空防御的重点是反舰导弹类目标。而编队防御反舰导弹时对舰空导弹最关心的性能指标为杀伤区纵深、单发杀伤概率、目标通道数、系统反应时间、杀伤区低界、最大航路捷径、抗干扰能力等7个指标。7个指标间无统一的度量标准，需先构建隶属度函数，再计算各个指标的隶属度。构建隶属度函数的方法有专家经验法、相对选择法、模糊统计法、因素加权法、例证法、二元对比排序法等多种[9]。其中，专家经验法优势比较突出，且符合舰空导弹类型优选的特点，本文采用此法建立指标隶属度函数。

3.1各指标隶属度

(1) 杀伤区纵深

舰空导弹杀伤区纵深越大越好，其隶属度函数为偏大型分布。通常，受地球曲率对雷达探测距离的影响，舰空导弹对掠海反舰导弹的实际杀伤区远界一般不超过30 km，而杀伤区近界受制导控制区间限制不小于1 km，则杀伤区最大纵深为29 km，以此距离作为杀伤区纵深隶属度为1的临界点。而最小纵深应满足2枚导弹齐射在近界与目标遭遇，设齐射间隔为2 s，则最小纵深0.6 km，以此距离为隶属度为0的临界点。假设11 km为最模糊点，则隶属度曲线上的3个元素为(0.6,0)，(10,0.5)，(29,1)，隶属度随杀伤区纵深呈非线性增长，且最模糊点后增长速度相对较慢，因此，选择顶部相对较平坦的升k次抛物线形作为杀伤区纵深隶属度函数，即

(6)

(2) 单发杀伤概率

舰空导弹单发杀伤概率与目标类型、目标运动特征、弹目遭遇点分布、制导系统制导误差、引战配合效率等多种因素有关[10]。舰空导弹对反舰导弹目标的单发杀伤概率分布范围为0.3～0.95，假设平均值为0.6。单发杀伤概率属于偏大型分布，为了体现该指标的敏感性，选取中段变化率较大的S形分布函数：

(7)

(3) 目标通道数

舰空导弹目标通道数是指武器系统可以同时跟踪或照射的目标数，而火力密度(火力通道数)是指单位时间内所能射击的目标数。如“阿利.伯克”级驱逐舰安装3个照射器，则目标通道数为3，宙斯盾级巡洋舰4个照射器，目标通道数为4。通常，舰空导弹目标通道数越多，抗击连续多目标的能力越强，属于偏大型分布，选取升半Γ分布函数为隶属度函数。目标通道数大于2个的舰空导弹武器系统称为多通道武器系统。通常，舰空导弹的通道数量多为4个，选取目标通道数4作为最具模糊点元素，则目标通道数隶属度函数为

(8)

(4) 系统反应时间

舰空导弹系统反应时间越短，快速反应能力越强，对目标可达成的射击次数越多，属于偏小型分布，选取降k次抛物分布函数。分别选取(2,1)和(12,0.5)为临界点，(20,0)为最模糊点，则隶属度函数为

(9)

(5) 杀伤区低界

杀伤区低界是舰空导弹能否拦截超低掠海反舰导弹的重要指标。超低空突防已成为对海攻击最重要的战术技术手段之一，与高空和中高空突防相比具有明显的优势，并能对舰空导弹的射击造成一定的困难。所以杀伤区低界越低越好，属于偏小型分布，选突防高度7 m为最具模糊点元素，突防高度3 m为隶属度1的临界点，选取偏小型正态分布为隶属度函数：

(10)

(6) 最大航路捷径

舰空导弹最大航路捷径是舰空导弹协同作战能力的重要度量，航路捷径越大可实现协同的范围越大，掩护其他舰艇的能力越强。显然，最大航路捷径隶属度属于偏大型分布，选取升半梯形分布为隶属度函数。最大航路捷径影响因素有舰空导弹过载，弹道设计特性、制导控制精度等，其取值不大于杀伤区远界，不小于杀伤区近界。而防御反舰导弹时，受发现目标距离(视距)的限制，其航路捷径远小于防御飞机平台的航路捷径。设防御反导航路捷径最小不小于2 km，最大不大于15 km，其函数为

(11)

(7) 抗干扰能力

抗干扰能力为定性指标，可采用9级区间标度法，以自然原点最小标度1的量化值为0，最大标度9的量化值为1。8个长度为0.125的区间，表示各标度的语义度量及量化值，如表1所示。由此计算得出的定性指标量化值范围为[0,1]，作为该指标的隶属度值。

表1　区间标度法的分级语义度量及量化值

假设舰空导弹有3种制导体制分别为：Ⅱ类(指令制导+主动雷达寻的)、II类(捷联惯导+半主动雷达寻的)和Ⅲ类(指令制导+TVM制导)。在抗干扰能力方面，第Ⅲ类体制相对Ⅰ，Ⅱ类均具有一定的优势，而I类相对II类具有优势[11-12]。则Ⅰ，Ⅱ，Ⅲ类制导体制的语义度量分别为“较好”、“中等”和“很好”，则隶属度值为0.625，0.5，0.875。

3.2各指标权重

确定各指标权重的方法有层次分析法、德尔菲法、熵值法、灰色关联分析法、主成分分析法和模糊聚类分析法等。其中层次分析法，把复杂问题按其内在逻辑关系将各因素划分成相关联的有序层次，

运用多位专家的知识、经验、信息以及对评价指标的内涵和外延的理解，对同一层次的各评价指标权重两两对比，从而使复杂问题条理化，其逻辑性强、可信度高，所以本文采用层次分析法确定各指标权重。

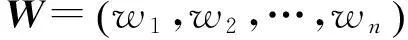
在计算判断矩阵的最大特征根λmax及其对应的特征向量W时，可采用多种方法计算，如和积法、幂指数法、方根法等。在保证精度要求的条件下，可使用和积法计算，其具体步骤为：

1) 将判断矩阵按列正规化：

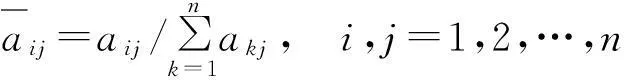
2) 正规化后的判断矩阵按列相加：

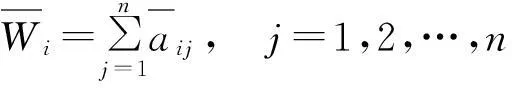
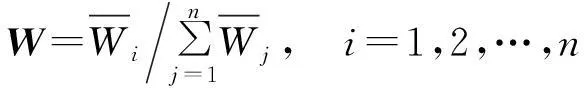
4) 计算判断矩阵最大特征根：

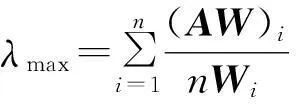
其中(AW)i为AW的第i个分量。

(3) 对判断矩阵进行一致性检验：计算一致性指标CI=(λmax-n)/(n-1)，与同阶平均随机一致性指标RI进行比较，其比值记为CR。当CR=CI/RI<0.10时，判断矩阵具有满意的一致性，否则需要对判断矩阵进行调整，如表2所示。

表2　平均随机一致性指标

对杀伤区纵深、单发杀伤概率、目标通道数、系统反应时间、杀伤区低界、最大航路捷径和抗干扰能力的权重进行两两比较，得决策矩阵：

(12)

根据上述步骤计算得，λmax=8.2，CR=0.021 6，则各指标权重向量为

(13)

4基于直觉模糊多指标决策计算和分析

假设3种类型的舰空导弹分别为A(Ⅰ类体制),B(Ⅱ类体制)、C(Ⅲ类体制)，其防御反舰导弹的战术技术性能参数如表3所示。

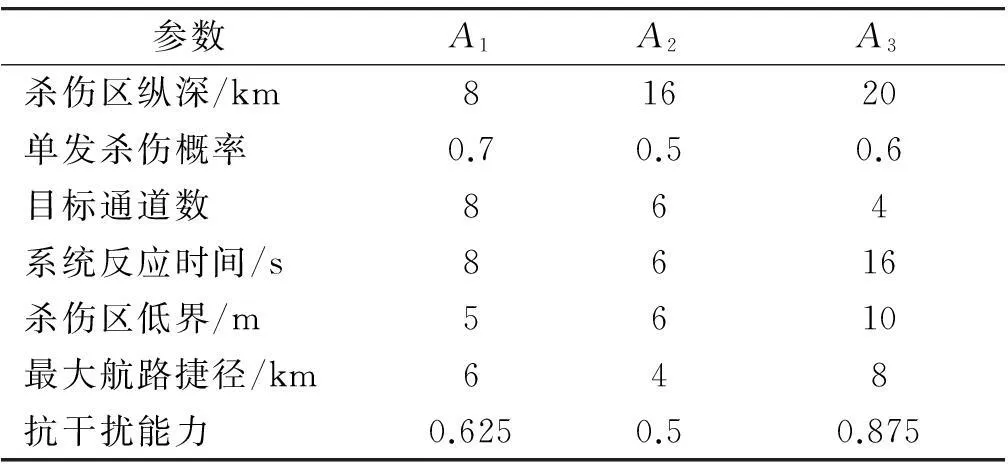
表3　备选舰空导弹性能

(1) 根据备选舰空导弹指标参数和隶属度函数计算各指标隶属度。为了使评估结果具有纵向可比性，在计算中设置一个理想型号的舰空导弹，即标准型号A0作为计算和衡量其它型号的基础和依据，其隶属度选为0.9，构建决策矩阵D：

(14)

(2) 对矩阵D规范化处理，得决策矩阵G：

(15)

(3) 对矩阵G位[0,0.382]区间的元素gij进行偏大型处理，得矩阵R：

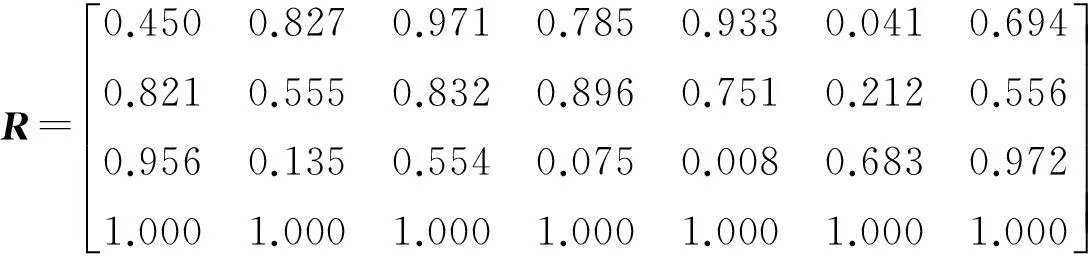
(16)

(4) 对矩阵R进行赋权处理，得矩阵Y：

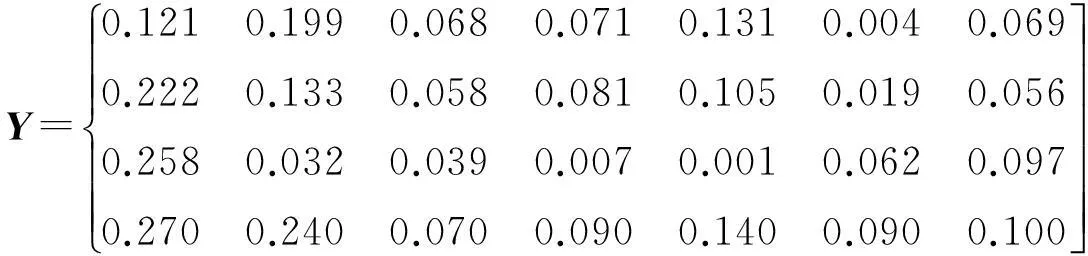
(17)

(5) 对决策矩阵Y按行规范化处理，得到矩阵H：

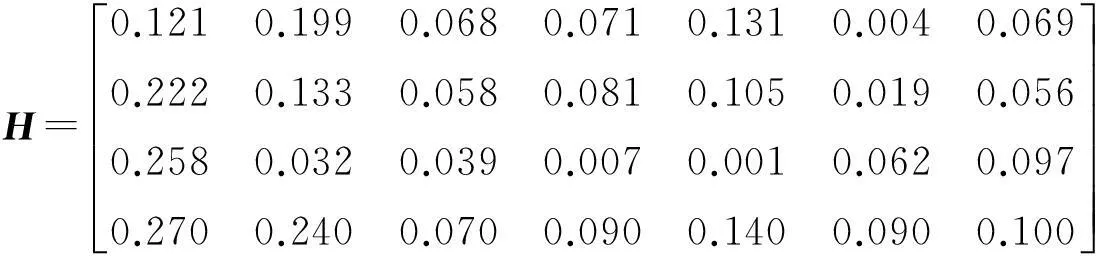
(18)

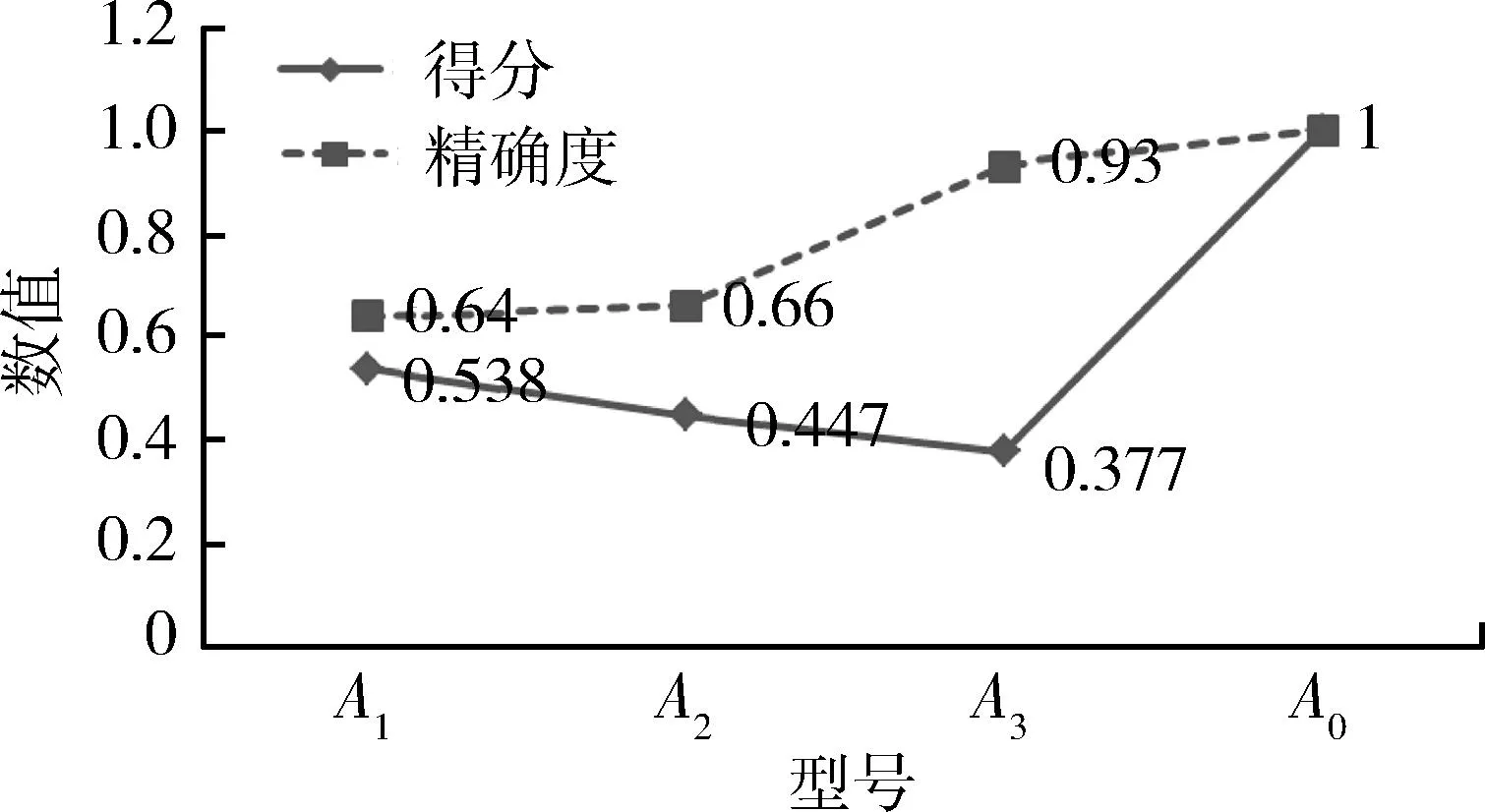
图1　各备选型号模糊得分和精确度Fig.1　Fuzzy score and degree of accuracy

通过图1得，适合编入编队的舰空导弹类型依次为：A1,A2和A3。A1型舰空导弹虽然杀伤区纵深较小，但目标通道个数多、单发杀伤概率高、杀伤区低界小，较其他舰空导弹在防御反舰导弹方面具有一定的优势。

5结束语

上述实例的计算结果合理，验证了模型的有效性和可用性。基于直觉模糊的类型优选模型，不但可用于舰空导弹的作战效能评估，对其他武器作战效能评估也同样具有一定的指导意义，并可为大型水面舰艇编队和HVU护航编队编成提供理论依据和方法指导。但模型在各指标隶属度函数的选择上，具有一定的主观性，隶属度函数的选择优化是进一步研究方向。

参考文献：

[1]ATANASSOV K T. Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96.

[2]ATANASSOV K T. More on Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems, 1989, 33(2): 37-45.

[3]马其东，方立恭，江言林. 基于直觉模糊多属性决策的作战效能综合评估方法[J]. 指挥控制与仿真, 2011, 33(2): 45-48.

MA Qi-dong, FANG Li-gong, JIANG Yan-lin. Method of Comprehensive Evaluation of Operational Effectiveness Based on Intuitionistic Fuzzy Sets Multi-Attributes Decision Making[J].Command Control & Simulation, 2011, 33(2): 45-48.

[4]雷英杰, 王宝树, 王毅. 基于直觉模糊推理的威胁评估方法[J]. 电子与信息学报,2007, 29(9): 2077-2081.

LEI Ying-jie, WANG Bao-shu, WANG Yi. Techniques for Threat Assessment Based on Intuitionistic Fuzzy Reasoning[J]. Journal of Electronics & Information Technology, 2007, 29(9): 2077-2081.

[5]雷英杰. 基于直觉模糊推理的态势与威胁评估研究[D].西安:西安电子科技大学, 2005.

LEI Ying-jie. Research on Threat Assessment Based on Intuitionistic Fuzzy Reasoning[D]. Xi′an: School of Computer Science and Engineering, 2005.

[6]万树平.直觉模糊多属性决策方法综述[J]. 控制与决策, 2010, 25(11): 1602-1604.

WAN Shu-ping. Survey on Intuitionistic Fuzzy Multi-Attribute Decision Making Approach [J]. Control and Decision, 2010,25(11): 1602-1604.

[7]林琳. 直觉模糊集在近似推理与决策中的应用[D]. 大连: 大连理工大学,2006.

LIN Lin.Intuitionistic Fuzzy Sets Applied in Approximate and Reasoning and Decision-Making[D].Dalian:Dalian University of Technology,2006.

[8]XU Ze-shui. Intuitionistic Preference Relations and Their Application in Group Decision Making[J]. Information Sciences, 2007(177): 2363-2379.

[9]王季方, 卢正鼎. 模糊控制中隶属度函数的确定方法[J]. 河南科学, 2000(4): 348-351

WANG Ji-fang, LU Zheng-ding. The Determine Method of Membership Function in Fuzzy Control[J]. Henan Science 2000(4): 348-351.

[10]徐品高. 关于地空导弹的最优单发杀伤概率问题[J]. 战术导弹技术, 1981(4):7-29.

XU Pin-gao. Optimal Single Shot Kill Probability of Surface-to-Air Missile [J]. Tactical Missile Technology, 1981(4):7-29.

[11]徐品高. 防空导弹总体设计[M]. 北京: 宇航出版社, 1996:116-133.

XU Pin-gao. The Overall Design of Air Defense Missile[M]. Beijing: China Astronautic Publishing House, 1996:116-133.

[12]陈立新.防空导弹网络化体系效能评估[M].北京：国防工业出版社，2007.

CHEN Li-xin.Effectiveness Evaluation of Network-Centric Air-Defense Missile Systems[M].Beijing:Nalional Defense Industry Press,2007.

Model of Ship to Air Missile System Optimal Selection for Task Group Based on Intuitionistic Fuzzy Sets

ZHONG Zhi-tong1, YANG Qing2,SUI Xian-hui1,ZHANG Xiao-dong1,

(1.Dalian Naval Academy,Liaoning Dalian 116018,China;2.South Sea Fleet Training Department,Guangdong Zhanjiang 510430,China)

Abstract:The nature of task group composition is to choose the type of ship to air missile for the air defense. The model of ship to air missile system optimal selection is built to resolve the problem of task group composition. Then the application verifies that the model is correct and efficient, and helpful to guide task group composition.

Key words:intuitionistic fuzzy sets; task group; ship to air missile system

中图分类号：E911；E917；TP391.9

文献标志码：A

文章编号：1009-086X(2015)-06-0209-06

doi:10.3969/j.issn.1009-086x.2015.06.037

通信地址：116018海军大连舰艇学院导弹系E-mail：flyskyzdx@126.com

作者简介：钟志通(1967-)，男，浙江武义人。副教授，博士，主要研究方向为舰载导弹武器。

*收稿日期：2014-03-06；修回日期：2014-10-29