气动参数不确定度对防空导弹制导精度的影响*1



气动参数不确定度对防空导弹制导精度的影响*1

吴玉亮，李向林，张庆兵

(北京电子工程总体研究所，北京100854)

摘要：防空导弹制导精度的提高对气动参数的精确性提出了更高的要求。在导弹的方案论证阶段，针对数值计算气动参数的不确定度进行了分析，并利用区间分析法得出不确定度范围。建立导弹制导控制六自由度仿真模型，完成不同速度区间下气动参数不确定度对防空导弹制导精度的影响分析。根据对仿真结果的分析，给出了在制导精度约束下，数值计算气动参数精细化设计方案。

关键词：气动数值计算；制导控制建模；制导精度；六自由度仿真；蒙特卡罗法；精细化设计

0引言

在导弹的方案论证阶段，气动参数的获取方式主要依靠数值计算方法，数值计算方法的原理是将气动经典理论中的非线性方程模型离散化成一组线性方程组，利用计算机强大的计算能力求解方程组。数值计算的条件易于控制，并可以进行多次重复试验，但是，数值计算也有其局限性，数值计算的数学模型和真实模型之间存在着一定的差距，在计算过程中会忽略一些次要因素来使模型简化，使计算结果和精确值相比存在着一定的误差，而气动参数是稳定控制系统设计的前提和依据，稳定控制系统的性能决定着导弹的制导精度，因此研究导弹气动参数的不确定度对制导精度的影响很有必要[1-2]。

在气动参数不确定研究方向上，参考文献[3-4]了解并研究了CFD 计算过程中不确定度分析的过程和细节，数值计算中采用多套网格，在此基础上， 进行了验证分析，评估了数值误差和数值不确定度。参考文献[5] 基于不确定度椭球导出的C-R(Cramer-Rao)预测参数的不确定度，并将C-R界修正方法应用于飞行实测数据。本论文中根据风洞试验和飞行试验参数辨识得到的气动参数作为参考值估计数值计算气动参数的不确定度。

在研究气动参数不确定性的影响分析时，国内外研究基本都是从控制系统的角度入手，参考文献[6-8]均通过采用现代控制理论的方法设计稳定控制系统，增加系统的鲁棒性，减小气动参数不确定度对控制系统的影响。本文通过使用经典的三回路稳定控制系统设计[9]，分析气动参数不确定度对控制系统和制导精度的影响。

1气动数值计算

1.1数学模型

使用ANSYS ICEM软件对导弹流场结构进行结构化网格划分，根据流场的特点，对弹体壁面进行加密处理以满足湍流模型的要求。在超声速流场中，根据工程经验第一层网格的厚度在0.1 mm以下，对弹体的头部和尾部，采用O网格划分，以保证整个流场网格的质量。图1显示了导弹的壁面网格结构。

图1　导弹壁面网格结构Fig.1　Structure of missile nearwall grid

使用Fluent软件，对导弹的流场进行数值计算，流场计算求解器选择三维、稳态、基于密度耦合的隐式方程求解，湍流模型选择k-ε模型，湍流项使用二阶迎风格式，计算收敛残差判定为1e-5。在选取外流场条件时马赫数的取值为0.3，0.6，0.8，1.3，2.0，3.0和4.0共7种状态，在对导弹的攻角进行取值时选用0°，5°，10°，15°，20°和30° 6种情况。2种工作模态进行组合共42种不同的外流场条件，对这些外场条件分别进行气动数值计算。在亚声速状态下仿真迭代25 000步，在超声速条件下仿真迭代20 000步，得出各状态点的法向力系数、轴向力系数和压心系数。图2反映了不同攻角下法向力系数随马赫数的变化图。

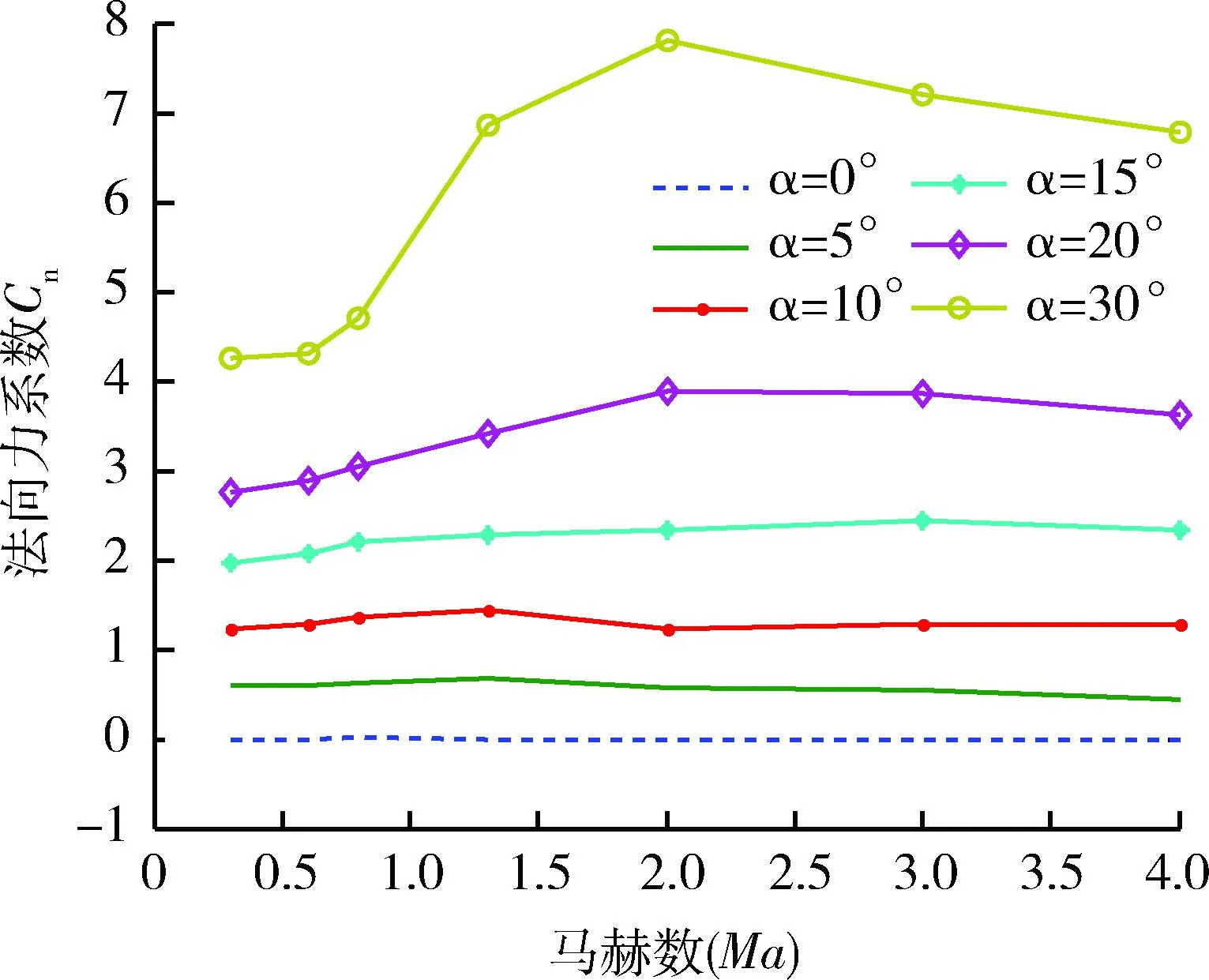
图2　不同攻角下法向力系数随马赫数变化图Fig.2　Variation of the normal coefficient with Mach　　　number at different attack angles

1.2气动参数不确定度分析

CFD数学模型的建立中湍流模型采用雷诺平均模型，该模型虽然计算量小，应用现有的计算机资源可以计算高雷诺数的复杂流动，在实际计算中发挥着重要的作用[10-11]，但却有2个主要缺点：

(1) RANS方法只给出了计算过程中的平均运动和相应的平均物理量，而不能给出需要的脉动量。而脉动量中包含湍流中大尺度涡结构，形态和尺度对于同一类型的湍流流动具有普遍性，其对湍流中的雷诺应力和能量、动量、质量等物理量的湍流输运过程做出了主要贡献，忽略这一大尺度涡结构会造成计算的不精确。

(2) 在模型的构造过程中，加入许多人为规定的假设，而这些假设与真实的物理模型间存在着一定的偏差，对计算结果造成一定的误差。在模型的构造中，将大小不同尺度的涡均同等对待，认为都是各项同性的。而在实际的模型中大小涡除了尺度上的明显差别外还有很大的区别，不可能找到一种湍流模型把对不同流动有不同结构的大涡特征统一考虑进去，不存在一种普遍使用的湍流模型。

同时在网格划分的过程中，质量不高的网格得到的数值解精度较低，使通过CFD计算得到的气动数据存在一定的不确定度。

数值解xc与真值C之差的绝对值的最大值称为不确定度，常用U表示，而不确定度区间即为(-U,U)，即

(1)

因CFD计算状态点数量较少，因此不确定度的置信度取100%，即认为不确定度区间中包含所有CFD计算数值解而没有遗漏。根据风洞试验和飞行气动参数辨识得到的气动参数作为参考真值，假设气动参数的不确定度在亚声速、跨声速和超声速区间内是独立的，图3反映了轴向力系数在攻角10°时的不确定度范围。

图3　轴向力系数及其不确定度范围Fig.3　Axial force coefficients and their　　　measurement uncertainties

通过计算得到气动参数不确定度在亚、跨、超3个速度区间内的分布规律，如表1所示。

表1　气动参数不确定度分布规律

2制导控制六自由度仿真

2.1制导控制模型

导弹的制导控制系统分为制导系统和稳定控制系统两部分，制导系统通过探测装置确定导弹相对目标的位置形成制导指令，在导引率设计上采用比例导引法[12]，弹目相对运动和导引关系方程为

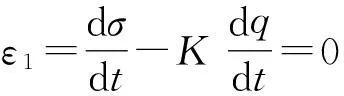
(2)

稳定控制系统是稳定导弹质心与姿态运动装置的总称，采用三回路稳定控制系统，以线加速度计的量测过载作为主反馈，实现稳定法向过载与参考输入之间的比例关系，角度反馈保证导弹的姿态角稳定，角速率陀螺反馈构成阻尼回路，改善弹体的等效阻尼特性[13]。俯仰通道稳定控制回路结构框图如图4所示。

图4　俯仰通道稳定控制回路框图Fig.4　Stabilization control loop in pitch channel

稳定控制回路的设计采用极点配置法，控制系统表达为状态空间描述，则弹体坐标系下各个姿态变量可以用一组微分方程描述[14-15]：

(3)

式中：a1，a2，a3，a4，a5为弹体动力系数，而导弹短周期运动的传递函数为

(4)

对于图4所示的三回路驾驶仪，将各系统的各路反馈等效到舵偏角处，系统的反馈可以表示为

(5)

式中：KD为舵机系统的比例系数，在这里KD=-3。状态反馈增益矩阵为

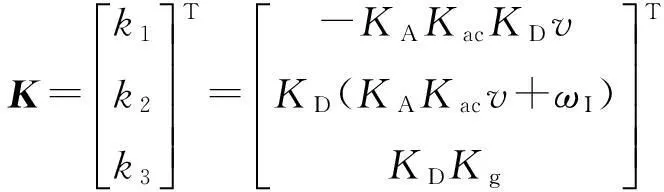
(6)

则自动驾驶仪的控制参数为

(7)

2.2仿真分析

根据动力学方程

可知，轴向力系数关系着导弹速度的变化量，因此轴向力系数的不确定度对飞行速度影响明显，导弹末速度随轴向力偏差的变化图如图 5所示，可知轴向力偏差与导弹末速度基本是线性关系。

图5　导弹末速度随轴向力偏差变化图Fig.5　Diagram of missile terminal velocity deviation　　　with axial force variation

由于制导控制回路是一个在气动参数不确定作用下的复杂非线性时变系统，同时考虑到系统的复杂模型，对这种系统的制导性能解析分析并不是轻而易举的，必须借助于仿真的手段分析气动参数不确定度对制导精度的影响。

给出导弹和目标的初始位置、速度信息，通过导弹制导控制仿真模型，分别只加入不同区间的气动参数误差，经过蒙特卡罗仿真(200次)，得出导弹的制导精度(最大值)，如表2所示。

表2　不同速度区间气动参数不确定度下的制导精度

结果表明，亚声速和跨声速的气动不确定度对制导精度影响很小，最大脱靶量均在0.5 m以内，而超声速的气动参数不确定度则对制导精度影响很大，最大脱靶量均大于2.8 m。图6表示超声速下法向力系数不确定度对制导精度影响蒙特卡罗仿真图。因为在导弹飞行过程中亚声速飞行时间只有3.7 s，而跨声速的飞行时间只有1.4 s，全程飞行时间均在25 s以上，并且制导控制系统会修正导弹姿态、位置偏差，使得最后的脱靶量变小。在气动参数不确定对制导精度影响重要程度排序上为轴向力系数>压心系数>法向力系数。

图6　蒙特卡罗仿真图Fig.6　Diagram of Monte Carlo simulation

2.3精细化设计仿真

通过仿真分析得出亚声速和跨声速的气动参数不确定度对制导精度影响很小，而超声速气动参数不确定对制导精度影响较大。因此采用精细化设计，缩小超声速段气动参数的不确定度范围，研究其对制导精度的影响，分析结果如表3所示。结果表明通过减小气动参数的不确定度能提高导弹的制导精度，若把导弹的制导精度(最大值)控制在1.5 m以内，则轴向力系数的不确定度范围需在(-4%，4%)以内，法向力系数的不确定度范围在(-4%，4%)以内，压心系数的不确定度范围在(-1%，1%)以内。

表3　气动参数不确定度精细化设计对制导精度的影响

3结束语

本文通过分析导弹气动参数的不确定度原因，得到各气动参数在不同速度区间内的不确定度范围。通过建立防空导弹制导控制系统数学模型，采用蒙特卡罗仿真法，得出不同速度区间各气动参数不确定度对制导精度的影响及影响程度。采用精细化设计方法，缩小超声速段各气动参数的不确定度范围能提高导弹的制导精度。并给出了将制导精度控制在1.5 m以内时，气动参数不确定度限制范围。本论文只分析了单个气动参数不确定度对制导精度的影响，而多种气动参数不确定度对制导精度的综合影响可以在以后的仿真中考虑。

参考文献：

[1]TANCREDI U. Allowable Aerodynamics Uncertainty Synthesis Aimed at Dynamics Properties Assessment for an Unmanned Space Vehicle[R]. AIAA 2004-6582.

[2]周明安. 地空导弹总体参数容差设计研究[J]. 战术导弹技术,1997(2):8-14.

ZHOU Ming-an. Study of Tolerance Design for Sam Overall Parameters [J]. Tactical Missile Technology, 1997(2):8-14.

[3]YAO Zhen-qiu, SHEN Hong-cui, GAO Hui. A New Methodology for the CFD Uncertainty Analysis[J]. Journal of Hydrodynamics,2013,25(1):131-147.

[4]张楠,沈泓萃,姚惠之. 阻力和流场的CFD不确定度分析探讨[J]. 船舶力学,2008,12(2):211-224.

ZHANG Nan, SHEN Hong-cui, YAO Hui-zhi. Uncertainty Analysis in CFD for Resistance and Flow Field[J]. Journal of Ship Mechanics,2008,12(2):211-224.

[5]王贵东,陈则霖,刘子强. 飞行器气动参数估计不确定度评价方法研究[J]. 航空学报,2013,34(9): 2057-2063.

WANG Gui-dong, CHEN Ze-lin, LIU Zi-qiang. Study on Uncertainty Evaluation Methods of Aerodynamic Parameter Estimation for Aircraft [J].Acta Aeronautica Et Astronautica Sinica, 2013, 34(9):2057-2063.

[6]袁国平,史小平. 带有特殊不确定性的导弹非线性自适应控制[J]. 电机与控制学报,2010,14(5): 104-108.

YUAN Guo-ping, SHI Xiao-ping. Nonlinear Adaptive Controller Design for Missile System with Special Uncertainties[J]. Electric Machines and Control,2010, 14(5): 104-108.

[7]胡云安,晋玉强,崔平远. 带有广义不确定性的导弹非线性控制系统设计[J]. 航空学报,2004,25(2):153-157.

HU Yun-an, JIN Yu-qiang, CUI Ping-yuan. Nonlinear Controller Design for Missile System with a General Set of Uncertainties [J]. Acta Aeronautica Et Astronautica Sinica,2004,25(2): 153-157.

[8]蔡建平. 带有气动参数不确定性的导弹自动驾驶仪设计[J]. 计算机测量与控制,2011,19(5): 1102-1105.

CAI Jian-ping. Adaptive Autopilot Design for Missile Systems with Aerodynamics Uncertainties [J]. Computer Measurement & Control,2011,19(5)：1102-1105.

[9]George M Siouris. 导弹制导与控制系[M].张天光,译. 北京:国防工业出版社,2010:72-82.

George M Siouris.Missile Guidance and Control Systems[M]. ZHANG Tian-guang, Translated. Beijing: National Defense Industry Press, 2010: 72-82.

[10]何佳丽,梁国柱,邱伟. 飞行器气动计算方法的应用研究[J]. 航空计算技术,2008,38(1):47-51.

HE Jia-li, LIANG Guo-zhu, QIU Wei. Study of Aerodynamic Characteristic Calculation Methods for Aircraft [J]. Aeronautical Computing Technique, 2008,38(1):47-51.

[11]王雄,李德波,罗坤. 圆孔射流近场湍流特性DNS与RANS模拟的对比研究[J]. 能源工程,2010(5):1-6.

WANG Xiong, LI De-bo, LUO Kun. Comparison of DNS and RANS Calculations of the Round Jet Flow in the Near Field Region [J]. Energy Engineering,2010(5):1-6.

[12]钱杏芳,林瑞雄,赵亚男. 导弹飞行力学[M]. 北京:北京理工大学出版社,2008:102-111.

QIAN Xing-fang, LIN Rui-xiong, ZHAO Ya-nan.Missile Flight Dynamics [M]. Beijing: Beijing Institute of Technology Press,2008:102-111.

[13]彭冠一. 防空导弹武器制导控制系统设计(上)[M]. 北京:宇航出版社,2005:7-18.

PENG Guan-yi. Guidance and Control System Design of Air Defense Missile [M]. Beijing: China Astronautics Publishing House,2005:7-18.

[14]林德福,王辉,王江. 战术导弹自动驾驶仪设计与制导律分析[M]. 北京:北京理工大学出版社,2012:45-49.

LIN De-fu, WANG Hui, WANG Jiang. Autopilot Design and Guidance Law Analysis for Tactical Missiles[M]. Beijing: Beijing Institute of Technology Press, 2012: 45-49.

[15]朱敬举,祁载康,夏群力. 三回路驾驶仪的极点配置方法设计[J]. 弹箭与制导学报, 2007, 27(4): 8-12.

ZHU Jing-ju, QI Zai-kang, XIA Qun-li. Pole Assignment Method for Three-Loop Autopilot Design[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2007,27(4): 8-12.

Effect of Dynamic Parameter Uncertainties on Air Defense Missile Guidance Accuracy

WU Yu-liang，LI Xiang-lin，ZHANG Qing-bing

(Beijing Institute of Electronic System Engineering, Beijing 100854, China)

Abstract:The improvement of air defense missile guidance accuracy raises greater demands on the aerodynamic parameters. In the missile demonstration stage, the computational fluid dynamic parameter uncertainties are analyzed, the uncertainty range is obtained with the method of interval analysis. The missile guidance and control model for six degree of freedom simulation is established. The effect of different speed intervals of aerodynamic parameter uncertainties on guidance accuracy is analyzed. According to the analysis of simulation results, the plan of computational fluid dynamics parameter detailed design is provided in the guidance accuracy constraints.

Key words:computational fluid dynamics; guidance and control model; guidance accuracy; six degree of freedom simulation; Monte Carlo method; detailed design.

中图分类号：V211.3; TJ765.3

文献标志码：A

文章编号：1009-086X(2015)-06-0043-06

doi:10.3969/j.issn.1009-086x.2015.06.008

通信地址：100854北京142信箱30分箱E-mail：yuliangwu@126.com

作者简介：吴玉亮(1988-)，男，河北衡水人。硕士生，主要从事飞行器设计研究。

基金项目：有

*收稿日期：2015-01-27；修回日期：2015-02-02