一种基于知识辅助的MIMO-STAP抗干扰算法*1



一种基于知识辅助的MIMO-STAP抗干扰算法*1

郝琳1，张永顺1，李哲1, 许洁2

(1.空军工程大学 防空反导学院，陕西 西安710051; 2.中国人民解放军93617部队，北京101400)

摘要：针对有源干扰环境下机载MIMO雷达的杂波抑制问题，利用预白化的思想，提出了一种基于知识辅助的MIMO-STAP抗干扰算法——KA-J-STAP方法，首先利用载机平台运动参数、雷达系统参数、干扰方位等先验信息构造相关协方差矩阵，后利用相关协方差矩阵对接收数据进行预白化，对杂波和噪声预置零，对于预白化后的数据空时自适应处理。仿真结果表明，相比于未采用知识辅助的算法，所提KA-J-STAP算法在干扰环境下仍能保持较好的杂波抑制性能。

关键词：机载MIMO雷达；预白化；先验信息；有源干扰

0引言

机载雷达常常处于下视工作的状态，如何抑制强烈的地杂波和各种类型的干扰是其面临的主要难题，而空时自适应处理(space-time adaptive processing)是解决该问题的关键技术[1-2]。MIMO雷达发射端的正交分集特性可以有效增大系统自由度[3-5]。这使得MIMO雷达在增强杂波与干扰抑制性能上具有极大潜力，为STAP技术带来了新机遇。2003年，Bliss D W首次提出MIMO-STAP的概念，将STAP技术应用于机载MIMO雷达中[6]。

随着电子信息技术的日益发展，机载雷达面临的电磁环境也日益复杂，除面临分布广、强度大的地(海)杂波外，同时还受到有意或无意的多种干扰。干扰如同杂波一样，直接影响雷达对目标的检测能力。因此，在存在干扰的复杂电磁环境下，STAP是否仍能具有较好的的杂波和干扰同时抑制能力是一个值得研究的问题。文献[7]提出了一种基于局部空域自适应阵列处理的改进型自适应波束形成方法，能有效估计出干扰源的方位，使STAP保持较好的杂波抑制性能。文献[8]对MIMO雷达杂波加有源干扰协方差矩阵的结构进行了分析，对于其秩的范围进行了估计，证明了MIMO雷达在干扰和杂波抑制上的优越性。

近年来，知识辅助STAP(KA-STAP)逐渐受到人们的重视[9-12]，主要分为间接应用先验知识的方法和直接应用先验知识的方法，前者包括智能样本选取和滤波器选择，后者包括贝叶斯滤波和数据预白化。本文提出的方法首先利用包含干扰信息在内的先验知识协方差矩阵对回波数据进行预白化处理，之后利用3-CAP方法对预白化后的数据进行空时自适应处理，达到杂波和干扰同时抑制的效果。

1机载MIMO雷达信号模型

正侧面机载MIMO雷达阵列天线几何模型图1，假设MIMO雷达载机以速度v向x向正方向做匀速直线运动，载机高度为h。杂波散射单元方位角为θ，俯仰角为φ，锥角为ψ。假设在一次相干处理时间(CPI)内，载机移动距离远小于雷达与杂波间的斜距，即雷达与杂波源相对几何关系近似不变。MIMO雷达收发天线均为正侧面均匀线阵，其中发射阵元总数为M，间距为dT,接收阵元总数为N,间距为dR，发收间距比α=dT/dR.时间域相干处理脉冲数目为K，且M个发射波形相互正交。

第k个(1≤k≤K)脉冲时，第n个(1≤n≤N)阵元接收到的来自第m个(1≤m≤M)阵元的数据可以表示为

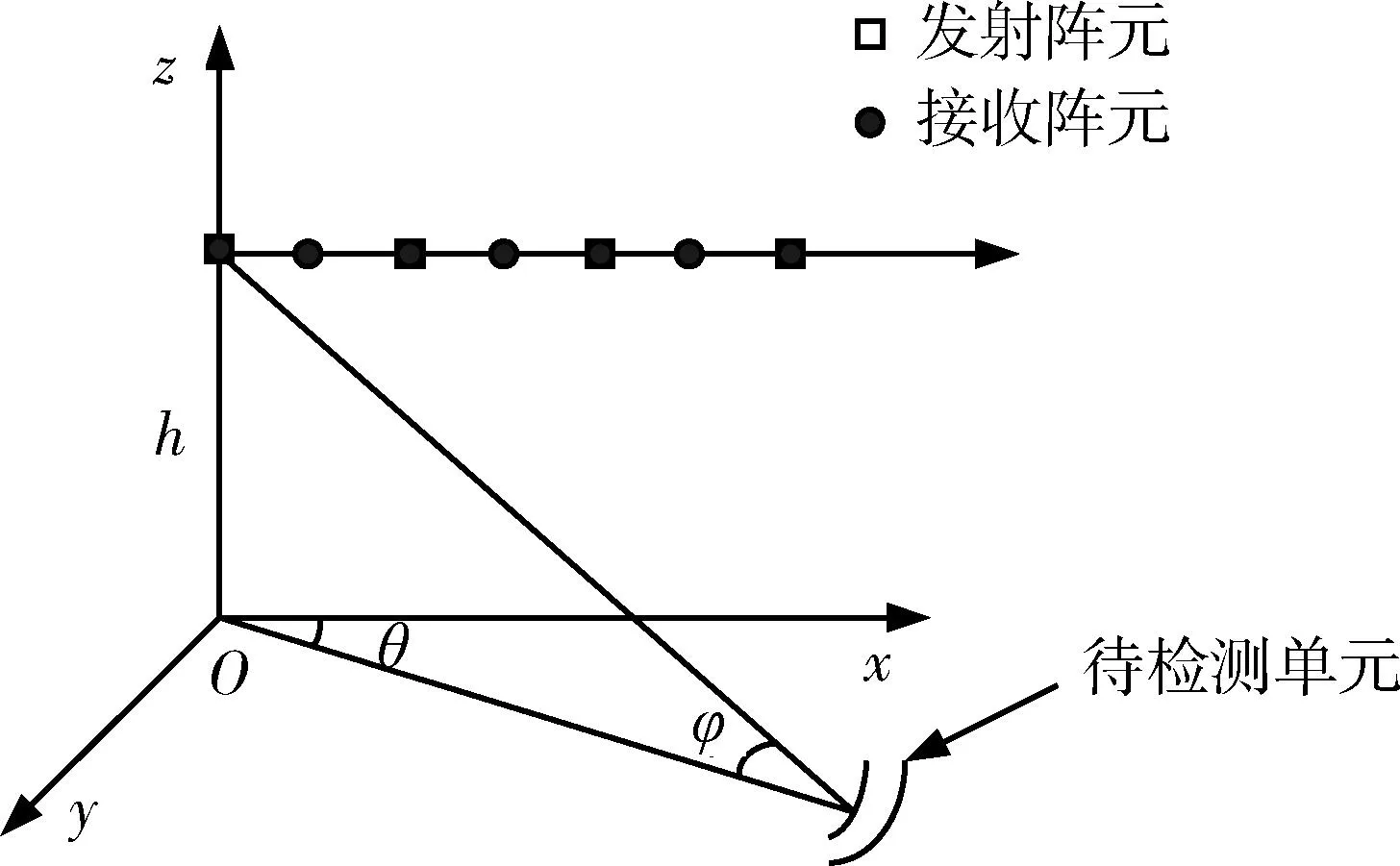
图1　机载MIMO雷达系统模型Fig.1　Model of airborne MIMO radar system

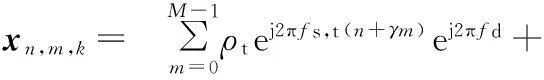
(1)

(2)

其中，ρt为目标反射信号幅度；vt为目标速度；Nc为距离环内的杂波块数目；ρi，θi和φi分别为第i个杂波块对应的反射信号幅度、方位角和高低角;fr为脉冲重复频率。式(1)中，第1项为目标回波信号，第2项为杂波回波信号，第3,4项为干扰和噪声分量。

将式(1)的接收信号排成一个列向量，则第p个距离环的接收向量为

xp=(x0,0,0，x1,0,0，…，xN-1,M-1,K-1)T.

(3)

2知识辅助的MIMO-STAP抗干扰算法

2.1机载MIMO雷达面临的干扰

干扰按照作用的原理分类可分为压制性干扰和欺骗性干扰。压制性干扰，又称遮盖性干扰，是用连续波信号或大量杂乱信号，压制或掩盖雷达目标信号，阻止雷达检测到真实目标。欺骗性干扰，又称模拟性干扰，它是施放和目标信号十分相似的干扰信号，使雷达操纵员难以辨别真假，将干扰误认为目标。本文主要研究存在压制性干扰情况下的杂波特性及针对压制性干扰的抑制问题。

点源压制干扰是压制性干扰中一种，它是分布在几个不同方向上的噪声干扰。图2中取干扰方向为0.3和0.6(方便起见，用方向余弦函数来表示方位向信息，以下同)，干噪比为60 dB。

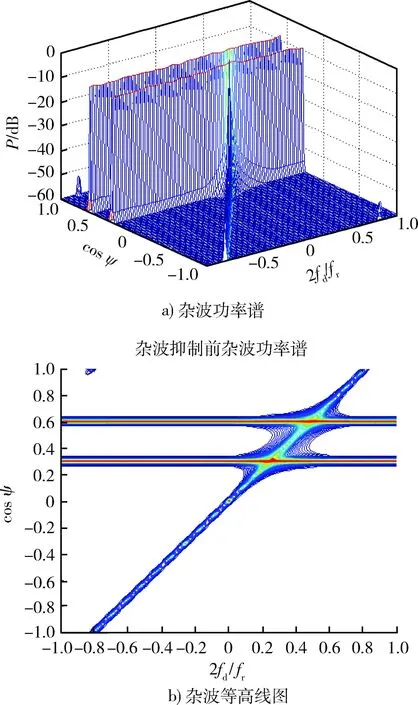
图2　点源压制干扰下杂波功率谱和其等高线图Fig.2　Clutter power spectrum and contour graph　　　in pointsource Jamming conditions

密集压制干扰不同于点源压制干扰，它通常是来自不同方向的少数几组干扰，每组均密集分布(甚至为连续分布)于一个小的角域内。在机载雷达的空时二维自适应处理种，对特定多普勒通道检测时，实际上杂波在空域的作用就相当于密集干扰(连片干扰)。图3中在方位向0.3～0.5内等间隔加21个干扰，干噪比为60 dB。

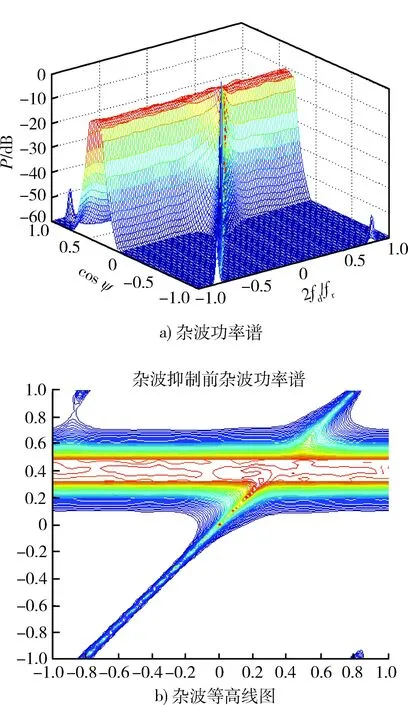
图3　密集压制干扰下杂波功率谱和其等高线图Fig.3　Clutter power spectrum and contour graph　　　in dense jamming conditions

在实际工程中，由于干扰使得杂波自由度增加，造成STAP算法所需要的独立同分布的训练样本数大大增加，导致直接利用STAP算法进行杂波与干扰的同时抑制的性能变差。

2.2干扰方位的确定

对于干扰源的定位问题，相关学者进行了大量研究，得出了很多有意义的结论，目前，主要由以下几种方案。一是在飞机上加装机载测向设备，利用飞机在空中进行干扰源的定位；二是在地面布设监测站，实现飞机可视区域的无缝隙覆盖；三是利用散射原理对飞机干扰信号进行监测和定位。前2种方法具有较高的定位精度，但是投资较大，系统运行成本高，最后一种方法投资较少，监测成本低，机动性较好。

2.3KA-J-STAP算法

预白化类的STAP方法不需要训练样本与先验协方差之间的统计模型，将原有的无约束或单线性约束最小化功率输出问题转化为多约束最优化问题[13]。本文所提出的KA-J-STAP方法就是利用预白化的原理，在干扰的位置上预置零后，再进行STAP处理，因此具有较好的抗干扰性能。算法流程如图4所示。

假设雷达系统、机载平台和干扰的相关参数是能够通过先验知识获得的，继而可以利用先验信息构造第p个距离环的相关矩阵模型:

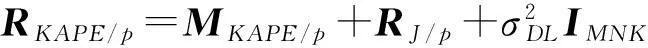
(4)

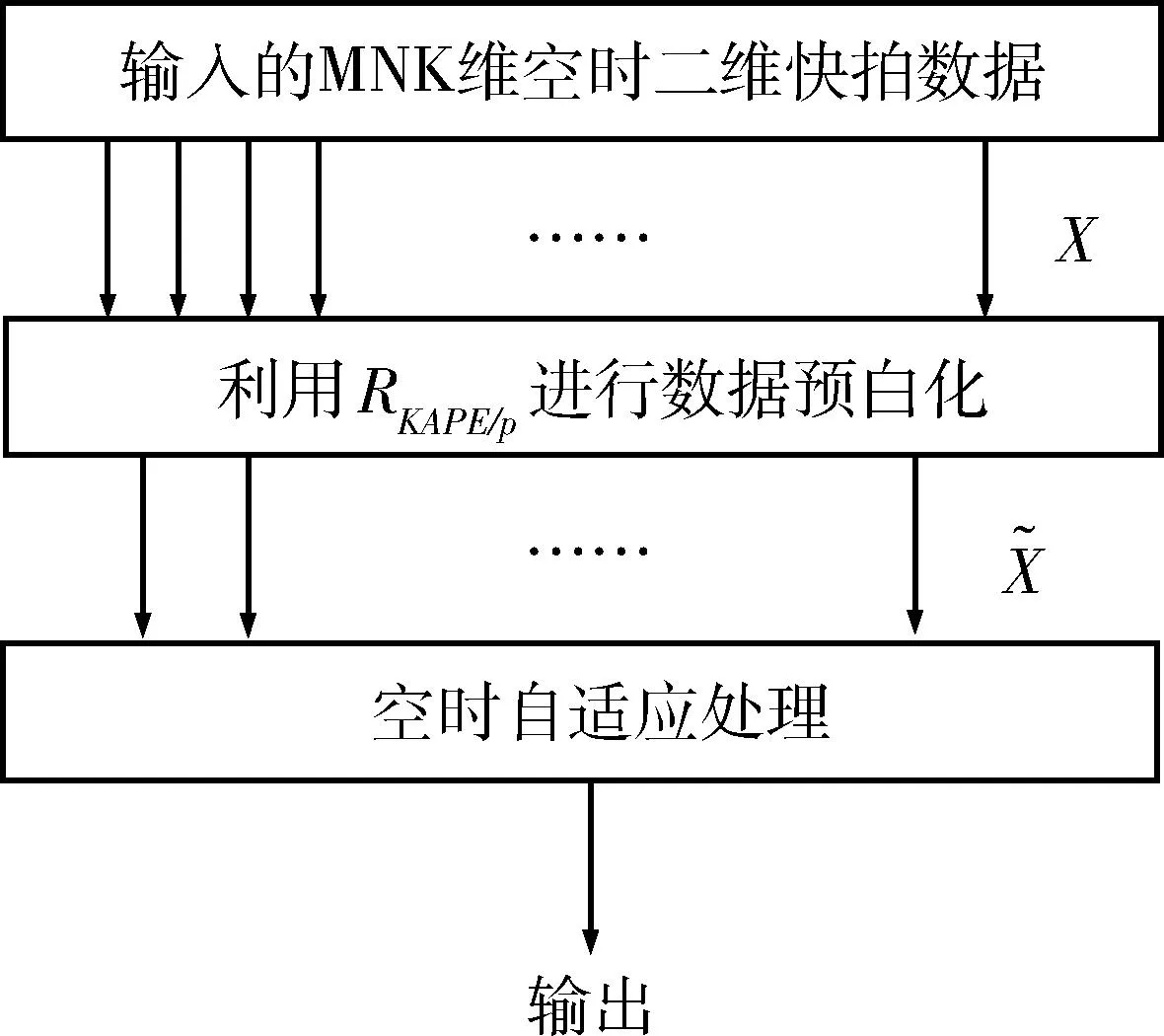
图4　KA-J-STAP算法流程Fig.4　Flow chart of KA-J-STAP

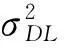
由于各种非理想因素的存在使得RKAPE/p与真实值存在偏差，根据CMT(协方差矩阵加权)理论，可以利用一个权矩阵T对RKAPE/p进行调整，从而使二维滤波器的凹口位置和宽度与实际杂波谱相符[14]。

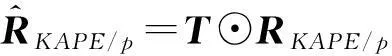
(5)

式中：⊙表示Hadamard积。

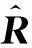
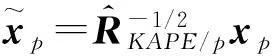
(6)

预白化后的协方差矩阵估计为

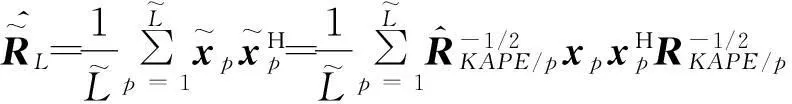
(7)

传统的预白化算法相关矩阵主要由先验杂波协方差矩阵和对角加载构成，本文所提KA-J-STAP算法创新性地在预白化矩阵中加入了干扰协防差矩阵，可有效增大自由度，降低样本需求量，在后续的STAP处理中，达到更好的干扰抑制性能。

3仿真及分析

基于Matlab仿真平台，利用本文提出的KA-J-STAP算法对杂波进行处理，并与未使用预白化滤波的典型算法进行比较。仿真参数如下：正侧视阵雷达情况下，发射阵元数M=4，发射阵元间距dm=0.8 m，发射全正交波形，接收阵元数N=4，接收阵元间距dn=0.1 m，发收阵元间距比γ=8，脉冲数K=8，载机飞行速度为140 m/s，工作波长λ=0.23 m，脉冲重复频率fr=2 434.8 Hz，杂噪比CNR=60 dB，干燥比JNR=60 dB。

3.1点源压制干扰下的杂波抑制

图5给出了存在点源压制干扰的情况下，KA-J-STAP与未采用预白化的传统STAP方法在改善因子方面的比较。

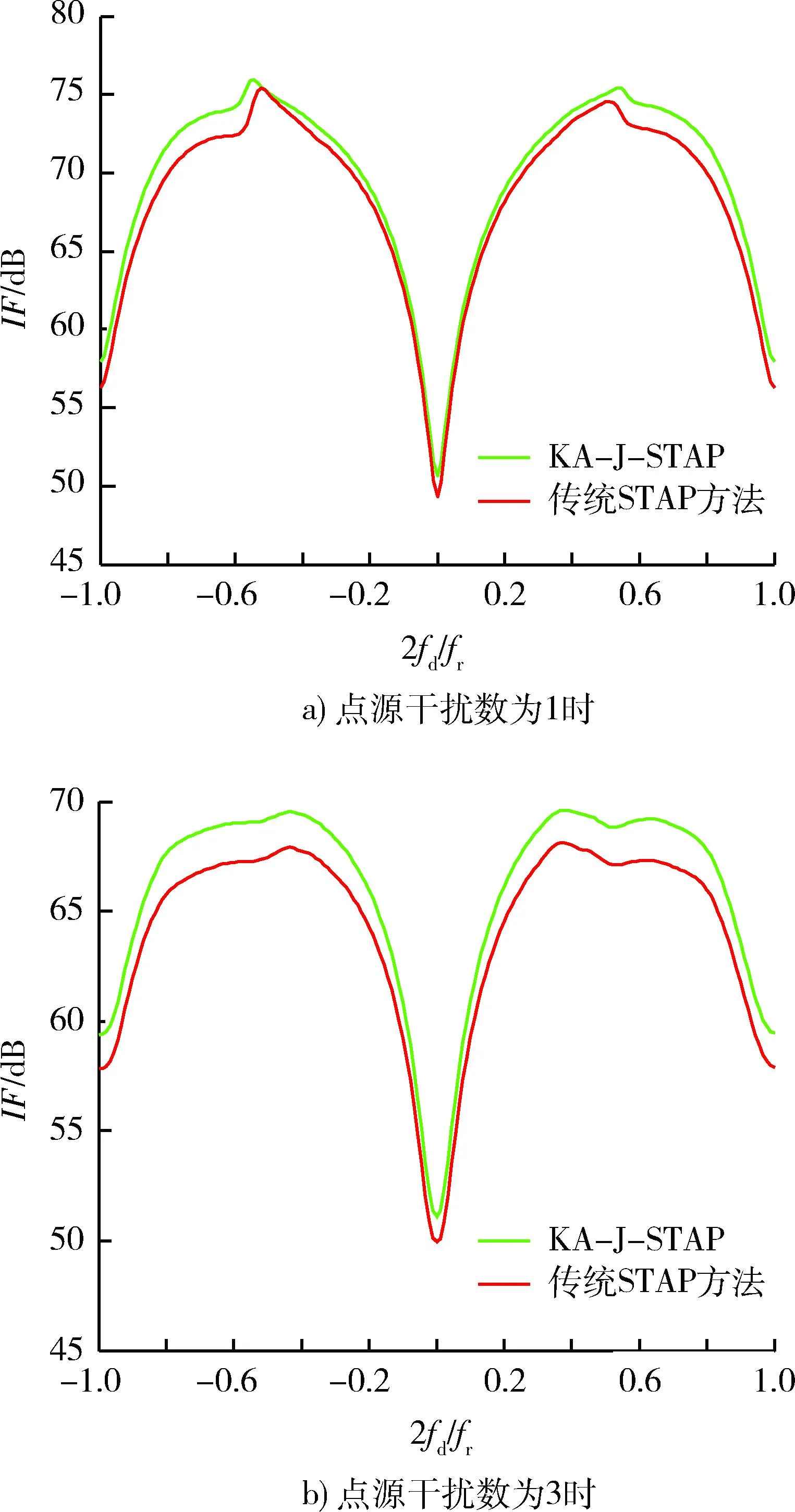
图5　点源压制干扰下的改善因子图Fig.5　Improvement factor in pointsource　　　　jamming conditions

由图4a)可以看出，由于干扰引起自由度的增加，使得传统STAP方法的杂波抑制性能下降，而采用预白化处理的KA-J-STAP方法在干扰环境下仍在主杂波区形成了较深的凹口，对于杂波和干扰的同时抑制能力较好。由图4可以看出随着干扰数的增多，两种方法的杂波抑制性能均有所下降，但KA-J-STAP的改善因子比于传统STAP方法高了2～3 dB，主杂波谱的展宽较小，能在主瓣内有效形成零点，因此， 具有较好的抗干扰能力。

3.2密集压制干扰下的杂波抑制

图6给出了存在点源压制干扰的情况下，KA-J-STAP与未采用预白化的传统STAP方法在改善因子方面的比较。

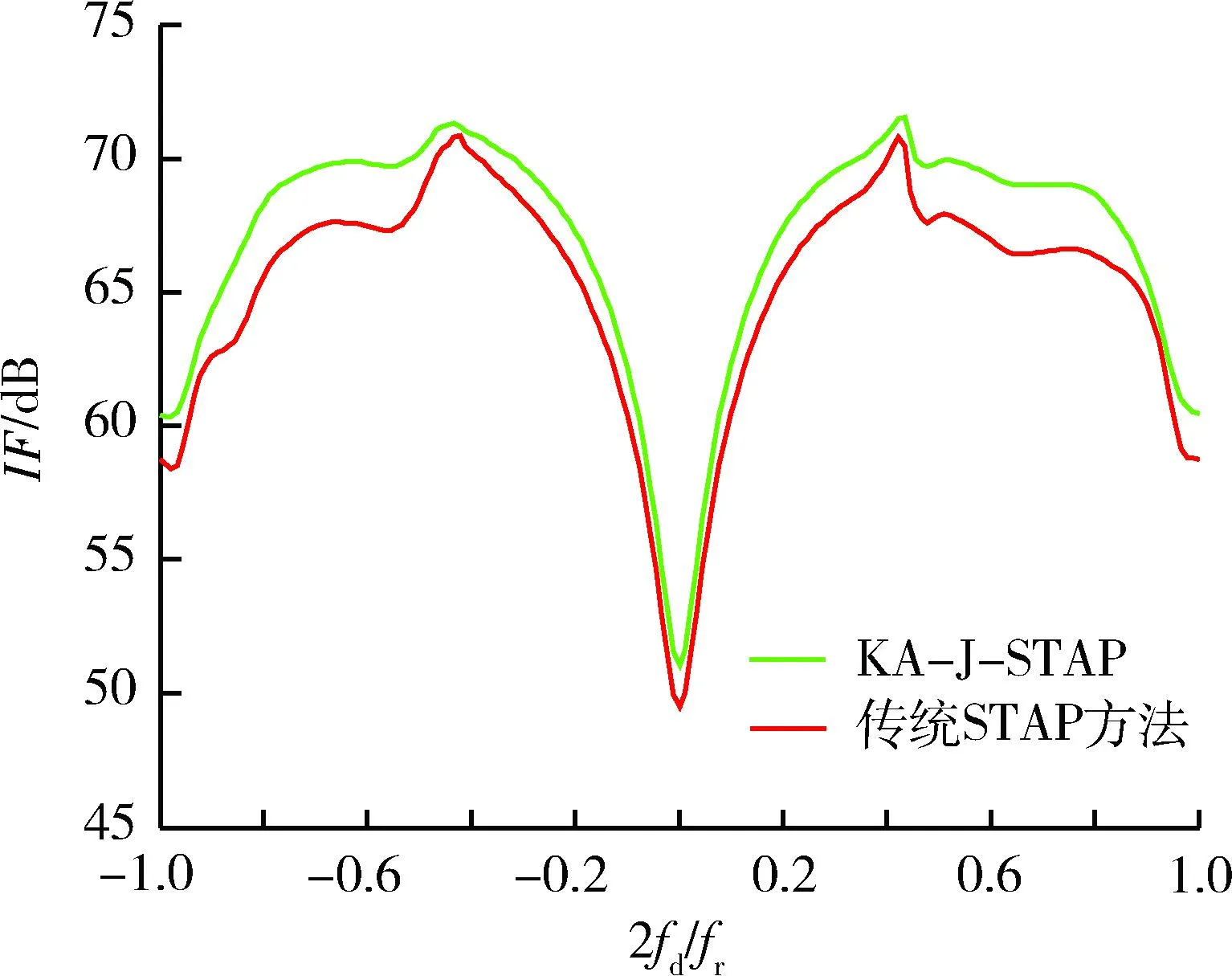
图6　点源压制干扰下的改善因子图Fig.6　Improvement factor in pointsource　　　jamming conditions

由图6可以看出，密集压制干扰使得杂波自由度增长更剧烈，对于杂波抑制提出了更大的挑战。而本文所提的KA-J-STAP方法主杂波区的展宽较小，相比于传统STAP方法，具有较好的杂波和干扰同时抑制能力 。

3.3先验协方差矩阵存在失配时的杂波抑制

前2个实验给出的是假设模型匹配时的杂波抑制性能，但在实际工程应用中很难做到先验协方差矩阵与真实协方差矩阵完全匹配，这就存在了失配的问题，在这种情况下对本文所提算法的杂波抑制性能进行了进一步的仿真，假设存在一个点源压制干扰的情况。

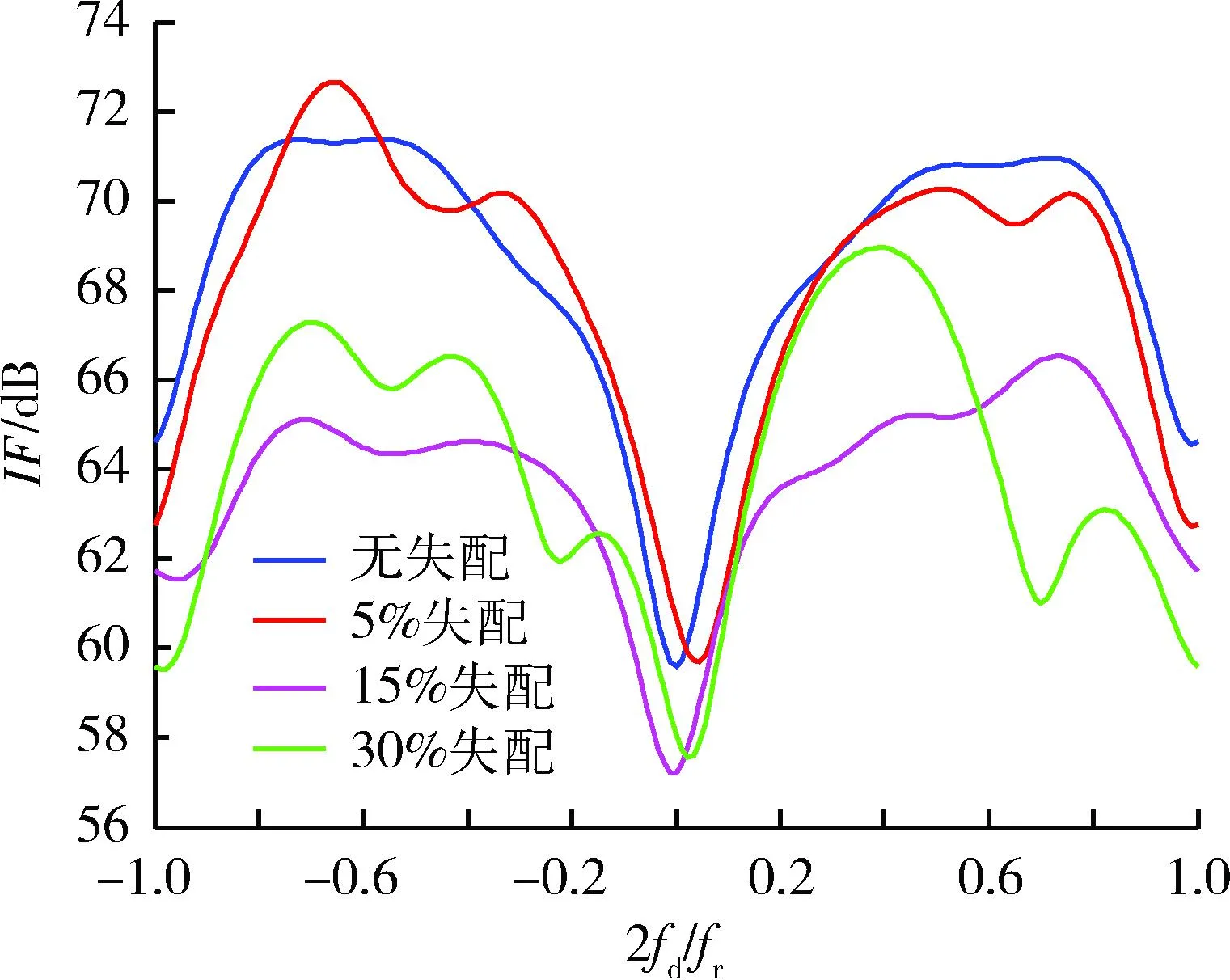
图7　不同失配情况下的改善因子图Fig.7　Improvement factor in different mismatch　　　conditions

由图7可以看出，随着先验协方差矩阵与真实值的失配度增加，系统的改善因子变差，但在5%的失配以内对系统整体性能影响不大。因此，对于先验模型的校准问题是以后的研究方向之一。

4结束语

本文针对机载MIMO雷达面临的有源干扰环境的挑战，通过利用知识辅助的预白化思想，提出一种MIMO-STAP抗干扰的有效方法——KA-J-STAP。仿真结果证明，相比于未采用预白化的传统STAP方法， KA-J-STAP能够有效提高系统自由度降低样本需求，在点源压制干扰和密集压制干扰的环境下都具有较好的杂波和干扰同时抑制性能。

参考文献：

[1]BRENNAN L E，REED I S. Theory of Adaptive Radar[J]. IEEE Trans AES, 1973,9 (3):237-252.

[2]王永良，彭应宁.空时自适应信号处理[M].北京： 清华大学出版社, 2000.

WANG Yong-liang,PENG Ying-ning.Space-Time Adaptive Processing[M].Beijing:Tsinghua University Press,2000.

[3]FISHIER E,HAINOVICH A,BLUM R.MIMO Radar:An Idea Whose Time Has Come[C]∥ Radar Conference 2004 Proceedings of the IEEE. Philadelphia IEEE Press ,2004 :71-78.

[4]FISHLER E, HAIMOVICH A,BLUM R S，et al. Performance of MIMO Radar Systems: Advantages of Angular Diversity[C]∥38th Asilomar Conferece Signals, Systems, Computers, Pacific Grove, CA, 2004：305-309.

[5]ROBEY F C, COUTTS S, WEIKLE D, et al.MIMO Radar Theory and Experimental Results[C]∥38th Asilomar Conference Signals, Systems, Computers, Pacific Grove, CA, 2004:300-304.

[6]BLISS D W,FORAYTHE K W.Multiple-Input Multiple-Output (MIMO) Radar and Imaging: Degrees of Freedom and Resolution[C]∥Proceedings of the 37th IEEE Asilomar Conference on Signals, Systems, Computers, Monterey, USA,2003:51-59.

[7]马汇淼，马林华，甘元，等.STAP技术在有源干扰环境下的运用方法[J].空军工程大学学报，2012，13(3)：65-69.

MA Hui-miao, MA Lin-hua, GAN Yuan,et al.A Method of STAP Application in Active Jamming Environment[J].Journal of Air Force Engineering University:Natual Science ed, 2012，13(3)：65-69.

[8]杨晓超，刘宏伟，王勇，等.有源干扰条件下机载MIMO雷达STAP协方差矩阵秩的分析[J].电子与信息学报，2012，34(7)：1616-1622.

YANG Xiao-chao, LIU Hong-wei, WANG Yong,et al.STAP Covariance Matrix Rank Analysis for Airborne MIMO Radar in the Presence of Jammers[J].Journal of Electronics&Information Technology, 2012，34(7)：1616-1622.

[9]GINI F,RANGASWAMY M.Knowledge Based Radar Detection,Tracking and Classification[M].USA:John Wiley Sons Inc,2008.

[10]陆达，张弓.知识辅助的机载MIMO雷达降秩STAP算法[J].数据采集与处理，2012，27(4)：429-435.

LU Da,ZHANG Gong.Knowledge-Aided Reduced-Rank STAP Algorithm for Airborne MIMO Radar[J].Journal of Data Acquisition & Processing, 2012，27(4)：429-435.

[11]ZHANG Xian-yi,WANG Xiao-hong,FAN Guo-zhong.Research on Knowledge-based STAP Technology[C]∥IET International Radar Conference,Guilin:IEEE Press,2009：1-4.

[12]BLUT S D,GERLACH K,RANGASWAMY M.STAP Using Knowledge-Aided Aonvariance Estimation and the FRACTA Algorithm[J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(3):1043-1057.

[13]范西昆，曲毅.知识辅助机载雷达杂波抑制方法研究进展[J].电子学报，2012，40(6)：1199-1206.

FAN Xi-kun,QU Yi.An Overview of Knowledge-Aided Clutter Mitigation Methods For Airborne Radar[J].Acta Electronica Sinica,2012，40(6)：1199-1206.

[14]MELVIN W,SHOWMAN G.An Approach to Knowledge-Aided Covariance Estimation[J].IEEE Transaction on Aerospace and Electronic Systems,2006,42(3):1021-1042.

Knowledge-aided MIMO-STAP Antijamming Algorithm

HAO Lin1，ZHANG Yong-shun1，LI Zhe1，XU Jie2

(1.AFEU, Air and Missile Defense College, Shaanxi Xi’an 710051, China;2.PLA,No. 93617 Troop,Beijing 101400,China)

Abstract:To solve the problem of clutter suppression of airborne MIMO radar in active jamming conditions, an MIMO-STA antijamming algorithm based on knowledge-aided KA-J-STAP is proposed by using the theory of pre-whitening.Firstly,the corresponding covariance model is formed by using the prior knowledge such as the characteristics of the radar system,aerospace platform and the direction of jamming.Then the corresponding covariance matrix is used to pre-whiten the received data. Finally,the spacetime adaptive processing is carried out on the pre-whiten data. Then simulation result shows that the algorithm proposed has better clutter suppression performance in jamming conditions.

Key words:airborne MIMO radar； pre-whiten; prior knowledge; active jamming

中图分类号：TN973；TP301.6；TP391.9

文献标志码：A

文章编号：1009-086X(2015)-06-0158-05

doi:10.3969/j.issn.1009-086x.2015.06.027

通信地址：710051陕西省西安市灞桥区长乐东路甲字1号空军工程大学防空反导学院研究生管理大队研究生一队E-mail：dearvic@126.com

作者简介：郝琳(1989-)，女，河北邯郸人。硕士生，主要研究方向为MIMO雷达空时自适应信号处理。

基金项目：国家自然科学基金(61372033)

*收稿日期：2014-07-26；修回日期：2014-11-19