一种新的k-means聚类雷达信号分选算法*1



一种新的k-means聚类雷达信号分选算法*1

张冉1，夏厚培2

(1.南京信息工程大学 电子与信息工程学院， 江苏 南京210044；

2.中国船舶重工集团 第七二四研究所，江苏 南京210003)

摘要：针对传统k-means聚类算法在雷达信号分选中应用存在的不足，提出了一种基于数据场和灰关联分析的k-means聚类雷达信号分选算法。该算法首先根据数据场理论计算所有数据样本的势值，寻找局域势值最大值，选取距最大值最近的样本数据作为初始聚类中心，局域势值最大值个数作为聚类数目；然后用灰关联度代替欧式距离来判断数据样本间相似性。该算法能够自动获取初始聚类中心和聚类数目，对频率捷变雷达具有较好的分选效果。仿真结果验证了算法的可行性。

关键词：雷达信号分选；k-means聚类；聚类中心和数目；数据场理论；灰关联分析；频率捷变

0引言

复杂电磁环境下雷达信号分选是雷达侦察系统的重要组成部分，只有在正确分选基础上，才能对雷达信号进行参数估计和提取[1]。在现代化战争中，新体制雷达大量出现并列入装备使用，信号形式复杂，脉冲密度越来越高，基于PRI单参数的传统分选方法已不能适应当前分选需要[2]。k-means聚类算法是一种无监督实时分类方法，该算法收敛快、易于实现、思想简单、不需要先验信息[3]，但聚类数目需要人为预先确定，初始聚类中心随机选取，数据样本相似性用多个参数的欧式距离来判断，但在空间距离上相近的数据并不一定具有高的相似性[4]，这些限制了k-means聚类算法在雷达信号分选中的应用。

为了解决k-means聚类算法在雷达信号分选中应用存在的问题，学者们提出来很多算法。文献[5]通过相像系数来代替欧氏距离，用小波系数和传统参数联合分选，分选准确率可达到96.2%，但该方法不能自动获取初始聚类中心和聚类数目。文献[6]联合蚁群算法和k-means聚类算法，用蚁群算法来确定聚类中心和聚类数目，得到了理想的分选效果，但数据样本相似性仍然用欧式距离来衡量。针对上述问题，本文将数据场理论和灰关联分析相结合应用到雷达信号分选中来，提出了一种新的k-means聚类雷达信号分选算法。该算法根据数据势场分布来得到初始聚类中心和聚类数目，用灰关联度来代替欧式距离来判断数据样本相似性。该方法能自动获取初始聚类中心，无需人为指定聚类数，不需要先验信息，对频率捷变雷达有较分选效果。

1k-means聚类原理

J.B.MacQueen提出的k-means算法是一种非监督实时聚类算法，在准则函数收敛基础上将数据样本分成m类[7-9]。设有n个PDW(脉冲描述字)样本集：

PDW=(PDW1,PDW2,…,PDWn)，

每一个PDW样本包含以下5个参数：到达时间(TOA)、脉冲频率(RF)、脉冲幅度(PA)、脉冲宽度(PW)、到达角(DOA),即PDWi=(TOAi,RFi,PAi,PWi,DOAi)，聚类数目m是预先确定的，随机选取m个初始聚类中心，按照最小距离原则将各样本归类到m个类的某一类，然后不断计算聚类中心和调整类，最后当各样本到各中心的距离平方之和最小时，分类结束。其步骤为：

(3) 重新调整分类后的各聚类中心：

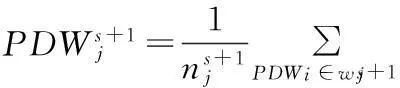
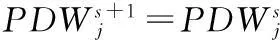
k-means算法是基于局部最优的聚类分析算法，不同的初始聚类中心和聚类数目可能得到不同的分析结果，因此合适的选取初始聚类中心和聚类个数显得尤为重要。

2新的k-means聚类雷达信号分选算法

2.1数据场

根据数据场理论，数据空间中的数据不是孤立的，而是通过数据场这个客观存在的媒介与其他数据相互作用[10-11]。类比物理学中的电场和引力场，定义数据间相互作用的影响函数为场强函数：

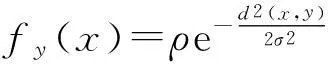
(1)

式中：σ为辐射因子；ρ反应数据点的数据量，一般取1；d(x,y)为欧式距离。

每一数据对数据场中其它任何数据都辐射能量，那么任一点的场强就是所有这些能量在此点的代数和，称为此处数据场的势，根据场强函数可以得到数据场的势函数：

(2)

式中：n为数据的数量。

由式(2)可知，势函数由位置和距离决定，势值大小和两者距离成反比。一般来说，势值大的区域数据密集，势值小的区域数据稀疏。

2.2初始聚类中心的确定

将数据场中势值相等的点连起来形成的线称为等势线，等势线围绕形成的不同中心称为势心[12]。势心是大量数据样本在一个或者一个以上的属性数据值中所体现出来的极值特征，单个数据的势心就是数据本身所在的位置，从等势线图中可以发现势心的位置，其数学语言描述为

Fmax≥Fy(i,j)，

(3)

式中：Fmax为势心值；Fy(i,j)为势心周围的势值；(i,j)为点的位置。

由式(3)可知，势心就是在一定范围内势值极大值点，通过势心就能确定初始聚类中心和聚类数目，但势值是叠加作用的结果，势心不一定和空间数据样本重合，应该选择距离势心最近的数据样本为初始聚类中心，数学表达式为

Dmin=d|Fmax,data(i,j)|，

(4)

Fcenter=data(i,j)，

(5)

式中：data(i,j)表示任意数据；d代表某种距离运算(这里采用欧式距离)；Fcenter为初始聚类中心。

2.3灰关联分析

传统的k-means聚类算法中，脉冲相似性常常用欧式距离来衡量，但在空间上相近的数据并不一定具有高的相似性，而灰关联度根据整体相似性来衡量数据之间的距离，能克服这个问题[13-16]。计算数据样本间灰关联度有以下几个步骤：

(1) 数据样本标准化处理

在实际的雷达信号侦察中，侦收到的信号比较复杂，不同参数数据不在同一数量级上，为保证数据具有可比性，在灰关联分析时，需要对数据集中所有参数维数进行归一化处理[12]，根据如下公式进行标准化处理：

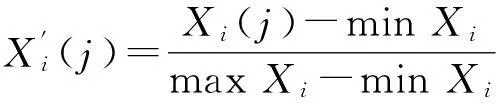
(6)

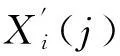
(2) 计算关联系数

将式(5)得到的Fcenter作为参考序列，为表示方便，这里表示为X0(j)，侦察雷达侦收到的序列Xi(j)作为比较序列，则第i个比较序列的第j维的绝对差为

Δi(j)=|X0(j)-Xi(j)|，

(7)

则两者关联系数为

(8)

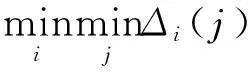
ξi={ξi(j),j=1,2,…,N}.

(9)

(3) 计算灰关联度

将各维的关联系数用一个值来表示，这个值就是灰关联度。Xi(j)和X0(j)的关联度为

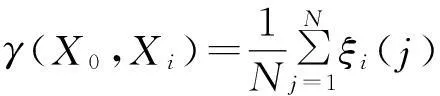
(10)

灰关联度越大，说明Xi(j)和X0(j)的相似性越大，反之越小。

2.4新的k-means聚类雷达信号分选算法

这里对传统k-means聚类算法进行改进，并应用到雷达信号分选中。首先通过数据场理论计算所有数据样本的势值，在一定范围内寻找势值最大值来确定初始聚类中心，势值最大值个数来确定聚类数目；再用灰关联度来描述脉冲间相似性。在侦收到的雷达信号5个参数：TOA，DOA，RF，PW，PA中，根据TOA可以得到脉冲重复频率(PRI)，PRI工作方式多、变化快，一般不作为分选的依据，PA随着天线的扫描而变化，因此本文用DOA，RF，PW进行分选。新的算法步骤如下：

(1) 根据DOA，RF，PW3个参数按照式(6)进行标准化处理。

(2) 按照式(2)计算每个数据点的势值，再根据式(4)，(5)找出距局域势值最大值最近的样本数据作为初始聚类中心，局域势值个数作为聚类数目。

(3) 根据式(7)～(10)计算每个样本数据和初始聚类中心的灰关联度，将灰关联度最大的划分到该聚类中心所在的类。

(4) 对于每一类，重新计算聚类中心，

若2次计算出的聚类中心没有变化，则聚类准则函数收敛，算法结束。否则转到步骤(3)。

3仿真分析

为验证本文方法的有效性，用Matlab进行仿真试验。在实际工程中，雷达体制复杂，脉冲流在时间上交错，并且脉冲部分参数交叠，例如2部频率捷变雷达参数在频域上交叠，因此这里选取4部频率捷变进行试验，在很短时间内，DOA可以认为是不变的，但是RF，PW是变化的，不考虑脉冲丢失，每部雷达信号参数都加入了测量误差，仿真参数如表1。

数据经标准化处理后，根据数据场理论通过势函数计算所有数据样本势值来描述雷达信号参数分布情况从而确定初始聚类中心和聚类数目，如图1～3所示。从图中可以比较直观的看到雷达信号可分为4类，通过计算距势值最大值点最近的样本数据可得到初始聚类中心，如表2。然后按照本文算法步骤(3)，(4)对数据进行分选，最终的聚类中心如表3。比较表2和表3可知，初始聚类中心选取是合理的。

图1　载频和脉宽等势线分布Fig.1　Equipotential line distribution of carrier　　　frequency and pulse width

图2　到达角和载频等势线分布Fig.2　Equipotential line distribution of arrival　　　angle and carrier frequency

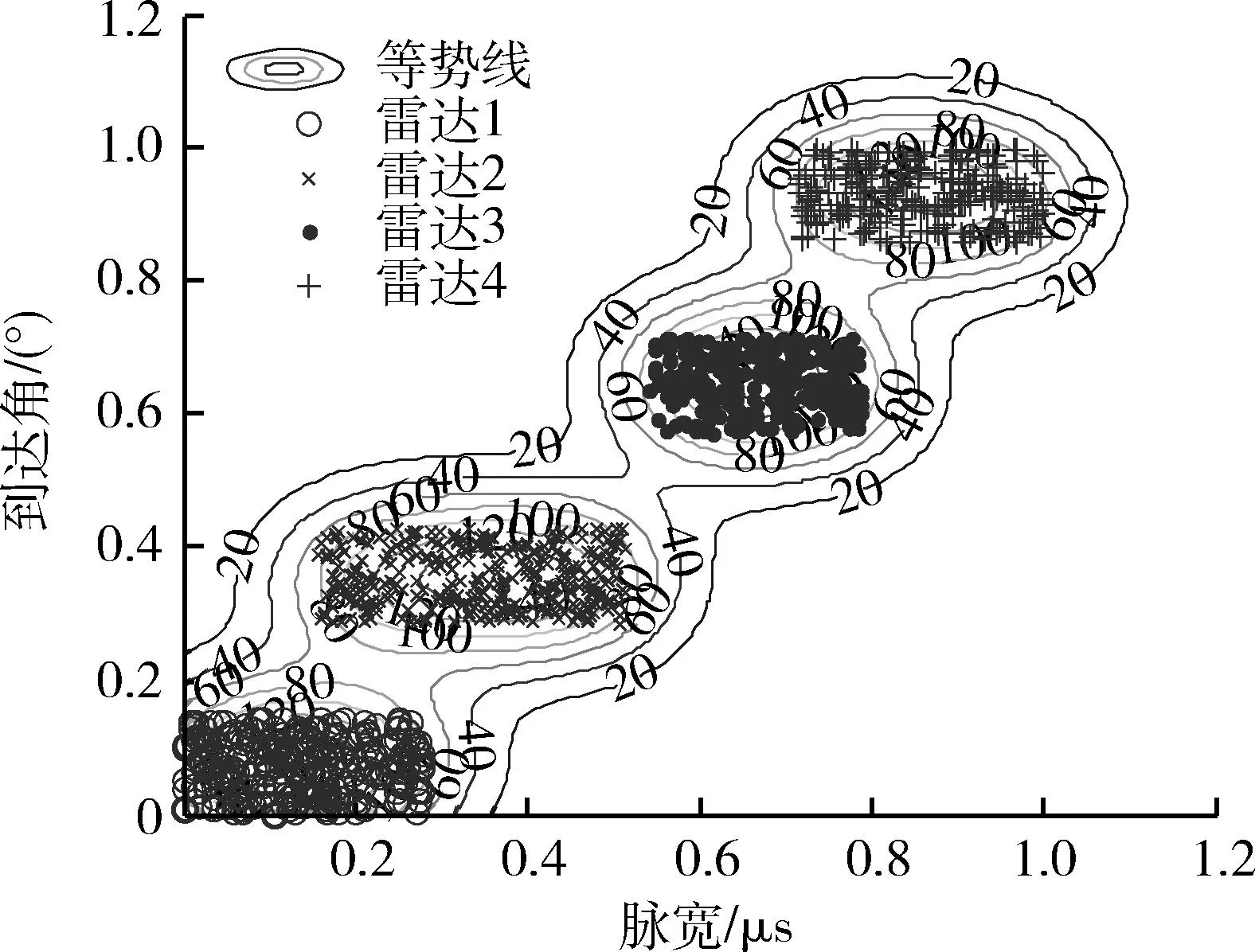
图3　脉宽和到达角等势线分布Fig.3　Equipotential line distribution of pulse　　　width and arrival angle

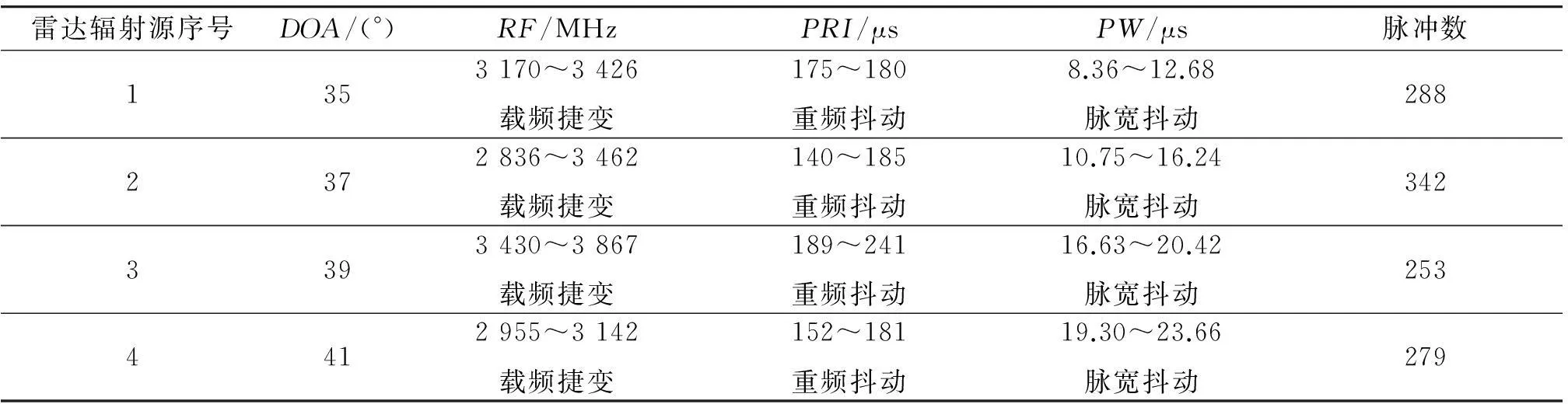
雷达辐射源序号DOA/(°)RF/MHzPRI/μsPW/μs脉冲数1353170～3426载频捷变175～180重频抖动8.36～12.68脉宽抖动2882372836～3462载频捷变140～185重频抖动10.75～16.24脉宽抖动3423393430～3867载频捷变189～241重频抖动16.63～20.42脉宽抖动2534412955～3142载频捷变152～181重频抖动19.30～23.66脉宽抖动279

表2　初始聚类中心

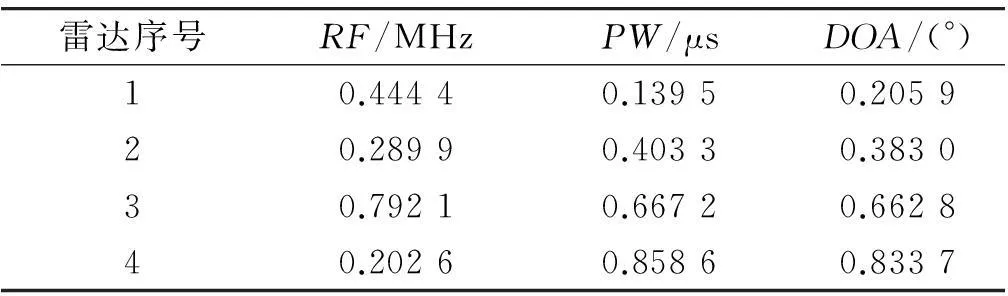
表3　最终聚类中心

为了比较本文算法和传统k-means算法的分选效果，用k-means算法处理试验数据，考虑到k-means算法随机选取聚类中心和聚类数目，会得到不同的结果，故这里仿真100次，然后取统计平均。所得分选结果和本文算法分选结果比较如表4所示。

表4　k-means算法和本文算法效果比较

从表4可以看出，本文算法迭代次数减少，正确分选概率得到提高。

4结束语

本文对在雷达信号分选中得到广泛应用的k-means算法进行了改进，首先用数据场理论自动获取初始聚类中心，确定聚类数目，然后用灰关联分析代替欧式聚类来判断脉冲相似性。本文算法能自动获取初始聚类中心，确定聚类数目，不需任何先验信息支撑，对单个参数不超过30%交叠或者2个参数不同时交叠的频率捷变雷达有很好的分选效果。文中的仿真实例证明了该算法的有效性。但本文算法也有局限性，因为没有考虑噪声孤立点对聚类中心的影响，故本文算法只适用于接收信号信噪比很高情况，若信噪比较低，要先将噪声孤立点去除，然后再用该算法。

参考文献：

[1]国强.复杂环境下未知雷达辐射源信号分选的理论研究[D].哈尔滨：哈尔滨工程大学，2007.

GUO Qiang.Signal Sorting Methods for Unknown Radar Emitters in Complex Environments[D].Harbin:Harbin Engineering University,2007.

[2]梅桂圆.密集信号环境下雷达信号分选算法[D].哈尔滨：哈尔滨工程大学，2011.

MEI Gui-yuan.Radar Signal Sorting Algorithm on Intensive Signal Condition[D]. Harbin:Harbin Engineering University,2011.

[3]JOSHUA Z H,MICHAEL K N,RONG Hong-qiang.Automated Variable Weighting in k-means Type Clustering[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2005,27(5):657-688.

[4]郭昆，张岐山.基于灰关联分析的多数据流聚类[J].模式识别与人工智能，2011,24(6),769-774.

GUO Kun,ZHANG Qi-shan.Multiple Data Streams Clustering Based on Grey Relational Analysis[J].Pattern Recognition and Artificial Intelligence, 2011,24(6),769-774.

[5]冯明月，何明浩，王冰切.基于改进相似熵的参数交叠雷达信号分选[J]. 电子信息对抗技术，2013,28(4):1-4.

FENG Ming-yue,HE Ming-hao,WANG Bing-qie.Radar Signal Sorting of Parameters Overlapping Based on Improved Similitiude Entropy[J]. Technology of Electronic Information Confrontation, 2013,28(4):1-4.

[6]赵贵喜，骆鲁秦，陈彬.基于蚁群算法的k-均值聚类雷达信号分选算法[J].雷达科学与技术，2009,7(2):142-145.

ZHAO Gui-xi,LUO Lu-qin,CHEN Bin.Radar Signal Sorting Based on Ant Colony and K-means Clustering[J].Science and Technology of Radar, 2009,7(2):142-145.

[7]GUO Qiang,ZHANG Xing-zhou,LI Zheng.SVC&K-Means and Type-Entropy Based Deinterleaving/Recognition System of Radar Pulse[J].Proceeding of IEEE International Conference on Information Acquisition,2006,20(1):742-747.

[8]孙鑫，侯慧群，杨承志.基于改进K-均值算法的未知雷达信号分选[J].现代电子技术，2010,17(3):91-93.

SUN Xin,HOU Hui-qun,YANG Cheng-zhi.Unknown Radar Signals Deinterleaving Based on Improved K-Means Algorithm[J]. Modern Electronic Technology, 2010,17(3):91-93.

[9]雍霄驹，张登福，王世强.一种新的雷达辐射源分选算法[J].现代防御技术，2011,39(3):148-151.

YONG Xiao-ju,ZHANG Deng-fu,WANG Shi-qiang.A New Method of Sorting Radar Emitter Signals[J]. Modern Defense Technology, 2011,39(3):148-151.

[10]吴鹏飞.数据场在聚类分析中的应用研究[D].包头：内蒙古科技大学，2010.

WU Peng-fei.Research of Data Field in Clustering Analysis[D].Baotou:Inner Mongolia University of Sciecce and Technology,2010.

[11]简艳，贾洪勇.一种基于数据场的k-均值算法[J].计算机应用研究，2010,27(12):4498-4501.

JIAN Yan,JIA Hong-yong.k-Means Algorithm Based on Data Field[J].Computer Application Research,2010,27(12):4498-4501.

[12]张红昌，阮怀林，龚亮亮.一种新的未知雷达辐射源聚类分选方法[J].计算工程与应用，2008,44(27):200-202.

ZHANG Hong-chang,RUAN Huai-lin,GONG Liang-liang.New Clustering Approach for Sorting Unknown Radar Emitter Signal[J].Computer Engibeering and Application,2008,44(27):200-202.

[13]陈昊，侯慧群，杨承志，等.基于改进灰关联的雷达辐射源识别方法研究[J].现代防御技术，2013,41(2):155-159.

CHEN Hao,HOU Hui-qun,YANG Cheng-zhi，et al.Radar Emitter Identification Based on Improved Grey Relation[J].Modern Defense Technology, 2013,41(2):155-159.

[14]关欣，孙祥威，曹昕莹.改进的k-mean算法在特征关联中的应用[J].雷达科学与技术，2014,12(1):81-85.

GUAN Xin,SUN Xiang-wei,CAO Xin-ying.A Novel Algorithm for Feature Association Based on Gray Correlation Cluster[J]. Science and Technology of Radar,2014,12(1):81-85.

[15]陈韬伟，金炜东，陈振兴.基于灰关联分析的雷达辐射源信号盲分类[J].计算机工程与设计，2009,30(20):4686-4689.

CHEN Tao-wei,JIN Wei-dong,CHEN Zhen-xing.Blind Classification of Radar Emitter Signals Based on Grey Relation Analysis[J].Computer Engineering and Design, 2009,30(20):4686-4689.

[16]郭昆，张岐山.基于灰关联分析的谱聚类[J].系统工程理论与实践，2010,30(7):1260-1264.

GUO Kun,ZHANG Qi-shan.Spectral Clustering Based on Grey Relational Analysis[J].Systems Engineering-Theory & Practice, 2010,30(7):1260-1264.

Radar Signal Sorting Algorithm of a New k-means Clustering

ZHANG Ran1, XIA Hou-pei2

(1.Nanjing University of Information Science & Technology,College of Electrics and Information Engineering,Jiangsu Nanjing 210044,China; 2. No.724 Research Institute of CSIC,Jiangsu Nanjing 210003,China)

Abstract:For the defects in the application of radar signal sorting of the tradition k-means clustering algorithm, a radar signal sorting algorithm of k-means clustering is put forward based on data field and grey relational analysis. Firstly potential value of all the data samplesis calculated with the algorithm based on data field theory, to find local maximum potential value, select the maximum value from the recent sample data as the initial clustering center, the number of local maximum potential value as the number of clustering. Then grey relational degree is used to determine the similarity between data sample instead of Euclidean. The algorithm can automatically obtain the initial clustering center and clustering number, so it has a good sort effect of frequency agility radar. The simulation results verify the feasibility of this algorithm.

Key words:radar signal sorting; k-means clustering; cluster center and number; data field theory; grey relational analysis; frequency agility

中图分类号：TN957.51；TP301.6

文献标志码：A

文章编号：1009-086X(2015)-06-0136-06

doi:10.3969/j.issn.1009-086x.2015.06.023

通信地址：210044江苏省南京市江宁区水阁路长青街30号E-mail：1044713043@qq.com

作者简介：张冉(1989-)，男，安徽安庆人。硕士生，主要研究方向为雷达信号处理。

*收稿日期：2014-11-06；修回日期：2015-02-06