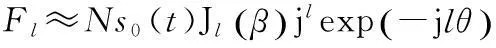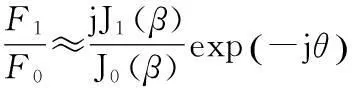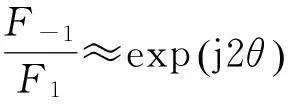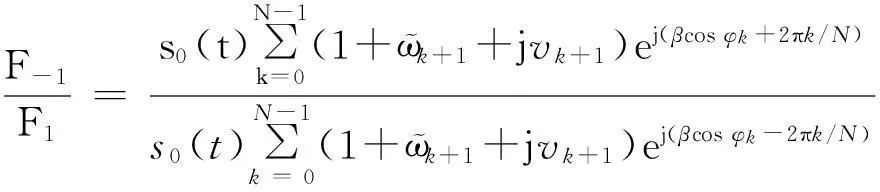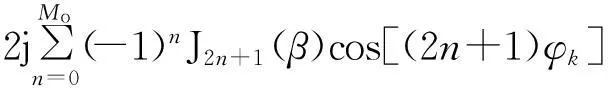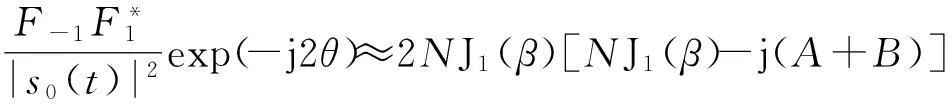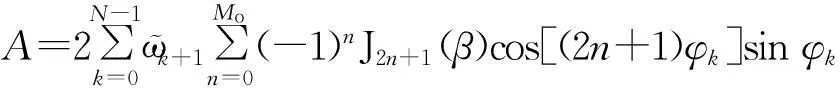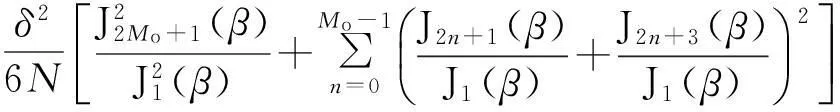通道幅相不一致时的全向测角误差分析*1



通道幅相不一致时的全向测角误差分析*1

田超，文树梁

(北京无线电测量研究所，北京100854)

摘要：在理想情况下，基于均匀圆阵的米波全向雷达可联合-1阶、0阶和和1阶相位模式实现全方位的无模糊测角。然而在实际工程中，各接收通道幅相特性往往不一致，这将导致激励出的相位模式中包含误差项从而引起明显的测角误差，而且该误差无法补偿，只能通过校正通道间的幅相误差或选择合适阵列参数的方式来减小。为此，通过理论推导得到测角误差与各接收支路幅相误差之间的解析关系式，明确了幅相误差对测角误差影响的同时也为合理选阵列参数以减小幅相误差引起的测角误差提供了理论依据，仿真分析验证了理论误差分析的正确性并给出了最优的阵列直径取值。

关键词：米波雷达；均匀圆阵；全向测角；相位模式；幅相不一致；测角误差分析

0引言

米波全向雷达因具有反隐身、抗反辐射导弹的能力以及其尺寸小、机动性强和研制成本低的特点而逐渐受到重视[1-3]。米波全向雷达利用均匀圆阵激励出的相位模式测角，但不同于一般基于均匀圆阵的超分辨测角算法利用了各阶相位模式[4-7]，其通过联合利用-1阶、0阶和1阶相位模式实现互耦条件下全方位无模糊测角。然而，实际工程中，各个接收通道的幅相特性不同，这使得激励出的相位模式存在误差项，从而导致测角误差的产生。现有关于均匀圆阵幅相误差对测角误差的分析一般只基于数值仿真且由于测角体制的不同，一些结论并不适用于米波全向雷达，文献[8]分析了幅相误差对均匀圆阵系统性能的影响，但其针对的是有指向性合成方向图，而米波全向雷达的天线波束则是方位全向的，文献[9]将幅相误差与互耦系数误差进行了等效，但对于米波全向雷达，幅相误差矩阵为对角矩阵，互耦矩阵为对称Toeplitz矩阵，二者无法等效。而文献[10-13]提出的各种幅相误差自校正算法虽可有效缓解幅相不一致的影响，但其校正一般并不在相位模式空间中实现，而米波全向雷达则是利用-1阶，0阶和1阶相位模式实现目标角度测量，而且幅相自校正的计算复杂度高，给信号处理能力提出了较高的要求。

因此，本文针对幅相不一致对测角的影响，先通过理论推导得到幅相不一致与测角误差间的解析关系，从而明确了幅相不一致引起的测角误差不仅与幅相不一致的程度有关，还与阵列的参数有关，进而考虑通过合理选择阵列参数的方式，在雷达设计阶段将幅相不一致的影响在统计意义上减至最小。

1无模糊方位全向测角原理

若发射信号为窄带信号，则阵元k接收到的信号可表示为

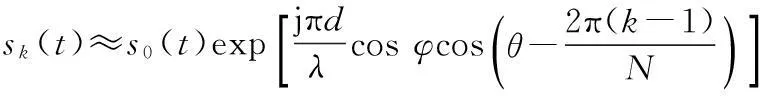
(1)

式中：k=1～N；λ为波长；s0(t)为相位中心接收的信号。

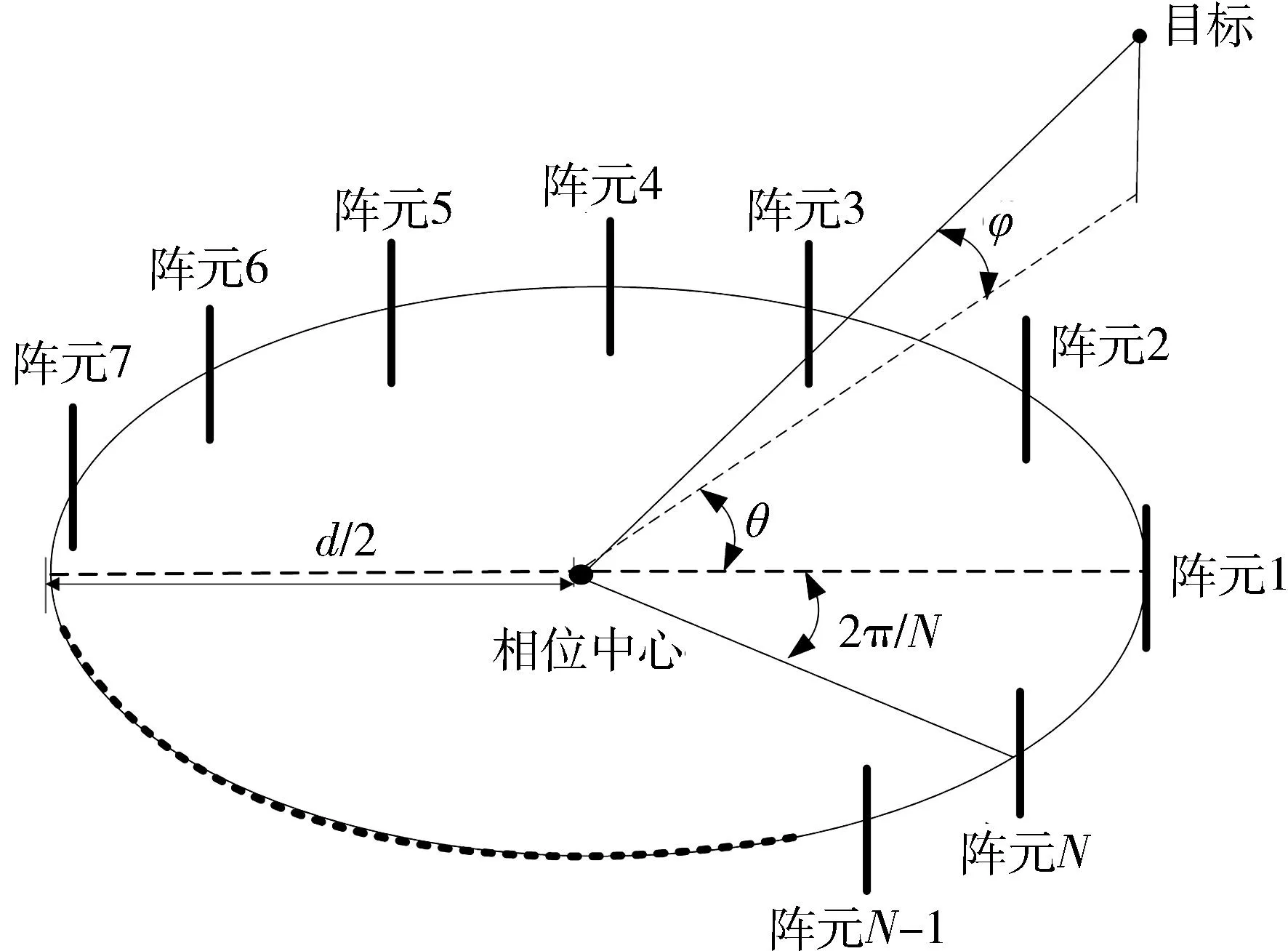
图1　N阵元均匀圆阵示意图Fig.1　Schematic map of uniform circular array　　　with N elements

根据均匀圆阵相位模式的相关理论[14-15]，各阶相位模式可通过阵元接收信号的FFT来实现，即有

(2)

若满足πd/λ

(3)

式中：l=-N+1～N-1；β=πdcosφ/λ;Jl(x)为第一类l阶贝塞尔函数。

考虑到s0(t)的相位未知，仅利用F1无法得到准确的目标方位角，因此为消除s0(t)相位的影响，可利用F1和F0。

(4)

然而，米波全向雷达出于机动性的考虑，天线阵列的口径往往较小，阵元间的互耦比较严重，在互耦系数未知的情况下，利用式(4)会产生较大的测角误差。

若阵列的互耦矩阵为

(5)

通过推导可以得到，考虑阵元间的互耦效应后：

(6)

由式(6)知，阵元间存在互耦时，κ的相位即为利用F1和F0测角产生的误差。

文献[1]证明，利用F1和F-1进行测角可以消除互耦的影响，即在阵元间存在严重互耦时亦有

(7)

但由式(7)知，利用F1和F-1进行测角虽消除了互耦的影响，但亦引入了π的测角模糊，因此需要联合式(6)的测角结果来解模糊。

具体的解模糊过程如下：记由式(7)求得的方位角在[0,π]范围内的值记为为θ1，由式(6)求得的方位角即为θ2，θ2∈[0,2π]。若|θ1-θ2|∈[0.5π,1.5π]，则判断方位角为θ1+π，否则，判断方位角为θ1。

综上所述，要获得精度高且无模糊的目标方位角，一方面要求θ1的精度高，另一方面要求θ2的误差不超过π/2。

为叙述方便，称利用F1和F0的测角方法为非对称式测角方法，称利用F1和F-1的测角方法为对称式测角方法。

2幅相不一致时的测角误差分析

实际工程中，各接收通道幅相特性并不完全一致，这将导致测角存在误差。出于减小幅相不一致引起的测角误差的需要，明确通道间幅相不一致与测角误差的关系十分必要。

若记第k个接收支路相对于参考通道的幅度为ak，相位为vk。假设ak均为[1-δ,1+δ]间的均匀分布，vk为[-σ,σ]间的均匀分布，且各ak，vk相互独立。若令ak=1+ϖk，则ϖk为[-δ,δ]间的均匀分布。

当各通道间的幅相不一致较小，即δ和σ较小时，有

akexp(jvk)≈1+ϖk+jvk.

(8)

考虑各接收支路的幅相不一致后，结合式(2)和式(8)可得新的对称式测角模型为

(9)

式中：φk=2πk/N。

根据贝塞尔函数的性质可知

(10)

将式(10)代入式(9)并通过推导可得

(11)

式中：

若记θΔ为测角误差，则可由式(11)得到

tan(2θΔ)=-2(A+B)/[NJ1(β)].

(12)

各通道间幅相的不一致较小时，|θΔ|亦较小，此时由式(12)近似可得

θΔ≈-(A+B)/[NJ1(β)].

(13)

由于ϖk，vk的均值为0且相互独立，因此容易得到A和B的均值亦均为0且相互独立，于是有

E(θΔ)=[E(A)+E(B)]/[NJ1(β)]=0，

(14)

Var(θΔ)=[Var(A)+Var(B)]/[NJ1(β)]2.

(15)

根据ϖk和vk分别为服从[-δ,δ]和[-σ,σ]间的均匀分布并利用各ϖk和vk间相互独立的特性，通过推导可得

(16)

由式(16)不难看出，幅相不一致对对称式测角误差的影响可分为两部分之和，一部分仅由幅度不一致决定，另一部分仅由相位不一致决定。

对于米波全向雷达，一般限定d/λ<1，此时，Me=1，Mo=2，式(16)可简化为

(17)

由式(17)知，在δ和σ固定的前提下，幅相不一致引起的测角误差可以通过N和β的合理取值尽量减小。

虽然N越大，幅相不一致的影响越小，但N的选取受到阵列直径、互耦的影响和测角方法的固有误差等因素的限制，因此，在探讨如何基于式(17)，通过阵列参数的选择来减小幅相不一致对测角精度的影响时，只重点考虑β。

β与阵列直径和波长的比值以及目标的仰角有关，然而，目标仰角为不可控制的因素且目标仰角的变化可等效为阵列直径与波长比值(简称直径波长比)的变化，因此，就对称式测角方法而言，阵列直径波长比的最优选择应使得式(17)最小。

尽管角度模糊可以解决的前提条件对非对称式测角方法的测角误差要求非常宽松，即不超过π/2，但考虑到阵元间的互耦严重，为了给天线设计提供尽量大的余量，往往希望包括幅相不一致在内的因素对测角精度的影响尽量地小。因此，幅相不一致对非对称测角精度的影响同样需要分析。

考虑各接收支路的幅相不一致后，结合式(2)和式(8)可得新的非对称式测角模型为

(18)

由于κ为常数，在考虑由幅相不一致引起的测角误差时，可不失一般性地令κ=1。此时，可以得到

(19)

若记θΔ为幅相不一致引起的测角误差，则可由式(19)得到

tanθΔ=(C+D)/N.

(20)

当各通道间幅相的不一致较小时，|θΔ|亦较小，此时由式(20)近似可得

θΔ≈(C+D)/N.

(21)

由于ϖk,vk的均值为0且相互独立，因此容易得到C和D的均值亦均为0且相互独立，于是有

E(θΔ)=[E(C)+E(D)]/N=0,

(22)

Var(θΔ)=[Var(C)+Var(D)]/N2.

(23)

根据ϖk和vk分别为服从[-δ,δ]和[-σ,σ]间的均匀分布并利用各ϖk和vk间相互独立的特性，通过推导可得

(24)

由式(24)不难看出，幅相不一致对非对称式测角误差的影响同样可分为2部分之和，一部分仅由幅度不一致决定，另一部分仅由相位不一致决定。若限定d/λ<1，则式(24)可简化为

(25)

为了解决对称式测角方法的测角模糊问题且给天线设计留有余量，同样需要将幅相不一致引起的非对称测角误差尽量控制在最小。因此，有必要通过阵列参数的选择，主要是阵列直径波长比，使得式(25)最小。

综合式(17)和式(25)可以看到：①采用对称式测角算法时，为减小幅度不一致的影响，阵列直径波长比的选择宜使U1(β)尽量大，为减小相位不一致的影响，阵列直径波长比的选择宜使U2(β)尽量大；②采用非对称式测角算法时，为减小幅度不一致的影响，阵列直径波长比的选择宜使U3(β)尽量大，为减小相位不一致的影响，阵列直径波长比的选择宜使U4(β)尽量大。

3仿真结果与分析

本节主要通过数值仿真为合理选择阵列直径波长比提供依据并验证所得到的幅相不一致引起的测角误差公式的正确性。

仰角为0°时，U1(β)和U2(β)随阵列直径波长比的变化分别如图2和图3所示。

图2　U1(β)随d/λ变化的曲线Fig.2　Curves of U1(β)changed with d/λ

图3　U2(β)随d/λ变化的曲线Fig.3　Curves of U2(β)changed with d/λ

对于对称式测角算法，由图2可知，d/λ越大，幅度不一致的影响越大，d/λ=0时幅度不一致影响最小；由图3可知，d/λ为0.7时相位不一致的影响最小。综合图2和图3可知，不存在d/λ的取值使得幅度不一致和相位不一致的影响同时最小。当需要综合考虑幅度和相位不一致时，d/λ的取值宜使U1(β)U2(β)最小。U1(β)U2(β)随阵列直径波长比的变化如图4所示。

图4　U1(β)U2(β)随d/λ变化的曲线Fig.4　Curves of U1(β)U2(β)changed with d/λ

由图4可知，对于对称式测角算法，若要求幅相不一致的影响综合最小，d/λ宜取0.61。

仰角为0°时，U3(β)和U4(β)随阵列直径波长比的变化分别如图5和图6所示。

图5　U3(β)随d/λ变化的曲线Fig.5　Curves of U3(β)changed with d/λ

图6　U4(β)随d/λ变化的曲线Fig.6　Curves of U4(β)changed with d/λ

对于非对称式测角算法，由图5可知，d/λ为0.38时幅度不一致影响最小；由图6可知，d/λ为0.4时相位不一致的影响最小。综合图5和图6可知，对于非对称式测角方法，同样不存在d/λ的取值使得幅度不一致和相位不一致的影响同时最小。当需要综合考虑幅度和相位不一致时，d/λ的取值宜使U3(β)U4(β)最小。U3(β)U4(β)随阵列直径波长比的变化如图7所示。

图7　U3(β)U4(β)随d/λ变化的曲线Fig.7　Curves of U3(β)U4(β)changed with d/λ

由图7可知，对于非对称式测角算法，若要求幅相不一致的影响综合最小，d/λ宜取0.39。

图随d/λ变化的曲线Fig.8　Curves ofUn(β)changed with d/λ

由图8可知，综合考虑幅度和相位不一致分别对非对称式和对称式测角算法测角误差的影响，阵列直径波长比的最佳取值应为0.44。在波长确定的情况下，阵列直径即可确定。

需要说明的是，当要求对目标有一定的仰角覆盖时，阵列直径波长比的选择应取得比0.44大。

为验证幅相不一致引起的测角误差公式即式(17)和式(25)的正确性，将公式计算的测角误差与数值统计的误差结果进行对比。

假设仰角为0°，阵列直径波长比为0.44，阵元数6，其中阵元数是按照固有误差不超过1°时所需最少阵元数的准则确定，具体可参考文献[1]。仅存在幅度不一致和仅存在相位不一致时，两种测角算法测角误差的公式计算值和数据统计值分别随最大幅度误差δ和最大相位误差σ变化的曲线对比如图9和图10所示。

图9　幅度不一致引起的测角误差Fig.9　Angle error caused by amplitude inconsistency

图10　相位不一致引起的测角误差Fig.10　Angle error caused by phase inconsistency

由图9和图10可知，幅度和相位不一致分别引起的测角误差，其公式计算值和误差统计值基本相同，由此证明了本文所得到的误差理论公式的正确性。另外，对比图9和图10可以发现，对于对称式测角，相位不一致比幅度不一致的影响更大；对于非对称式测角，幅度不一致比相位不一致影响更大。

本文出于为天线设计留有余量的考虑才对幅相不一致引起的非对称式测角误差提出了更高的要求。若实际工程中，阵元间互耦的影响可适当控制在较小范围，那么可以降低对幅相不一致引起的非对称式测角误差的要求，此时，阵列直径波长比的选择可主要以对称式测角算法对各通道幅相误差的要求为参考。

4结束语

联合均匀圆阵激励出的-1阶、0阶和1阶相位模式可实现方位向的无模糊全向测角，但各接收通道存在幅相不一致时会引入测角误差。本文通过分析幅相不一致与测角误差的关系，推导得到了二者之间的解析表达式并通过数值仿真验证其正确性，同时得到了幅相不一致影响下阵列参数的最优取值，为系统阵列参数的最终确定提供了一定参考。

参考文献：

[1]田超, 文树梁. 米波圆阵雷达全向测角算法及其性能分析[J]. 系统工程与电子技术, 2013, 35(12): 2507-2512.

TIAN Chao, WEN Shu-Liang. Omni-Directional Angle Measurement Algorithm of Meter-Wave Circular Array Radar and Its Performance Analysis[J]. Systems Engineering and Electronics, 2013, 35(12): 2507-2512.

[2]CHEN B X, ZHAO G H, ZHANG S H. Altitude Mea-surement Based on Beam Split and Frequency Diversity in VHF Radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 3-13.

[3]胡晓琴, 陈建文, 王永良,等. MIMO体制米波圆阵雷达研究[J]. 国防科技大学学报, 2009, 54(1): 52-57.

HU Xiao-qin, CHEN Jian-wen, WANG Yong-liang,et al. Research on the Meter-Wave Circular Array Radar for MIMO Systems[J]. Journal of National University of Defense Technology, 2009, 54(1): 52-57.

[4]MATHEWS C P, ZOLTOWSKI M D. Eigenstructure Techniques for 2-D Angle Estimation with Uniform Circular Arrays[J]. IEEE Transactions on Signal Processing, 1994, 42(9):2395-2407.

[5]PESAVENTOAND M, BOHME J F. Direction of Arrival Estimation in Uniform Circular Arrays Composed of Directional Elements[C]. Proc of Sensor Array and Multichannel Signal Processing Workshop Proceedings, 2002:503-507.

[6]GOOSSENS R, ROGIER H. A Hybrid UCA-RARE/Root-MUSIC Approach for 2-D Direction of Arrival Estimation in Uniform Circular Arrays in the Presence of Mutual Coupling[J]. IEEE Transactions on Antennas and Propagation,2007, 55(3): 841-849.

[7]WANG B H, HUI H T, LEONG M S. Decoupled 2D Direction of Arrival Estimation Using Compact Uniform Circular Arrays in the Presence of Elevation-Dependent Mutual Coupling[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(3): 747-755.

[8]李颖, 黄晓涛, 周智敏. 幅相误差对均匀圆阵系统性能的影响[J]. 雷达科学与技术, 2005, 3(2): 123-127.

LI Ying, HUANG Xiao-tao, ZHOU Zhi-min. Effect of Amplitude and Phase Errors on the Performance of Uniform Circular Array[J]. Radar Science and Technology, 2005, 3(2): 123-127.

[9]高火涛, 柯亨玉, 杨子杰,等. 互耦系数误差与通道幅相误差的等效关系[J]. 武汉大学学报:理学版, 2002, 48(1): 121-124.

GAO Huo-tao, KE Heng-yu, YANG Zi-jie, et al.The Relationship Between Mutual Coefficient Errors and the Amplitude and Phase Errors of Channels[J]. Wuhan University Journal:Natural Science ed, 2002, 48(1): 121-124.

[10]LU Zu-kun,JIANG Hong, GAO Ying. Amplitude and Phase Errors Self-Correcting Algorithm Based on the Uniform Circular Array[C]∥Proc of 2nd International Conference on Computer Science and Network Technology, Changchun, 2012: 136-140.

[11]DU Yong-xing, XI Xiao-li, XI Wen-jing. The Correction of Mutual Coupling and the Amplitude and Phase error Based on Digital Beamforming Receiving Antenna[C]∥Proc of 10th International Symposium on Antennas,Propagation & EM Theory , 2012: 231-233.

[12]鲁祖坤, 高鹰, 肖剑,等. 基于均匀圆阵的幅相误差自校正算法[J]. 火控雷达技术, 2013,42(1): 1-5.

LU Zu-kun, GAO Ying, XIAO Jian, et al.Amplitude and Phase Error Auto-Calibration Algorithm Based on Uniform Circular Array[J]. Fire Control Radar Technology, 2013, 42(1): 1-5.

[13]陈德莉, 卢焕章, 张聪. 多径条件下基于WSF的均匀圆阵幅相误差自校正[J]. 系统仿真学报, 2008, 20(17): 4563-4565.

CHEN De-li, LU Huang-zhang, ZHANG Cong.UCA Gain/Phase Self-Calibration in Presence of Multipath Based on Weighted Subspace Fitting[J]. Journal of System Simulation, 2008,20(17): 4563-4565.

[14]DAVIES D E N. A Transformation Between the Phasing Techniques Required for Linear and Circular Aerial Arrays[C]∥Proc of the Institution of Electrical Engineers, 1965, 112(11): 2041-2045.

[15]DU K L. Pattern Analysis of Uniform Circular Array[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(4): 1125-1129.

Error Analysis of Omni-Directional Angle Measurement with Amplitude and Phase Inconsistency between Channels

TIAN Chao，WEN Shu-liang

(Beijing Institute of Radio Measurement, Beijing 100854, China)

Abstract:In ideal scenarios, unambiguous azimuth angle is available by using the phase mode -1, 0 and 1 based on the omni-directional VHF radar with uniform circular array. However, in engineering, the amplitude and phase character of each receiving channel is usually different. This inconsistency may cause some errors of the measured angle. Moreover, the errors can’t be compensated and can only be decreased by calibrating the inconsistency or choosing the array parameters. For this purpose, the specific relationship between angle error and amplitude and phase inconsistency is deduced theoretically so that a theoretical reference is provided for the optimal selection of array parameter in order to reduce the angle error. Simulation results demonstrate the correctness of the deduced formulas and the optimal diameter of the array is also given.

Key words:VHF radar; uniform circular array; omni-directional angle measurement; phase mode; amplitude and phase inconsistency; angle error analysis

中图分类号：TN953+.5；TP391.9

文献标志码：A

文章编号：1009-086X(2015)-06-0104-08

doi:10.3969/j.issn.1009-086x.2015.06.018

通信地址：100854北京市142信箱203分箱1号E-mail：qctchao87@126.com

作者简介：田超(1987-)，男，湖北黄冈人。博士生，主要研究方向为雷达总体技术。

*收稿日期：2014-11-03；修回日期：2015-12-08