相控阵雷达导引头的惯性视线重构*1



相控阵雷达导引头的惯性视线重构*1

邵真杰，赵明元

(北京电子工程总体研究所，北京100854)

摘要：针对弹载相控阵雷达导引头的惯性视线重构问题，提出了基于Unscented卡尔曼滤波(UKF)的视线重构方法。与传统方法相比，提出的方法无需对导引头测量的角信息使用微分网络，避免了对测量噪声的放大。仿真结果表明，该方法可有效地重构视线角，从而进一步提高视线转率的估计精度。

关键词：相控阵雷达导引头；视线重构；视线转率估计；非线性滤波；UT变换；无迹卡尔曼滤波

0引言

相控阵雷达导引头属于捷联式导引头，它采用电扫描代替机械扫描，具有体积小、视场大、跟踪快、可实现多目标跟踪等优点，能大幅提高导弹的总体战术技术指标[1-3]，但机械稳定平台的取消也使其失去了直接测量惯性视线转率的能力。

捷联式导引头通常只能直接获取相对于弹体的视线角信息，为了获取比例导引规律所需的惯性视线角速率，理论上可以利用坐标变换重构惯性视线角，然后利用微分网络完成惯性视线转率的提取，然而直接微分会造成噪声的放大，使得重构精度难以满足要求。为此，国内外一些学者研究了利用卡尔曼滤波理论来估计视线转率的方法，但这些文献主要集中于研究捷联光学导引头“仅测角”条件下的视线转率估计，而未能利用主动雷达导引头所能提供的相对距离和距离变化率信息[4-10]；杨雅君等人虽然在可测距条件下研究了相控阵雷达导引头的视线转率提取方法[11]，但该方法忽略了弹体姿态的量测噪声，且选取稳定坐标系中三个轴向的位置、速度和加速度作为状态变量，不仅加剧了量测方程的非线性特性和状态间的耦合，也使得状态变量高达9维，且应用无迹卡尔曼滤波(unscented kalman filter,UKF)时的增广状态变量阶次还会更高，这就对弹上机的处理能力提出了很高的要求，限制了该方法的应用。

针对上述问题，本文选取惯性视线角及其变化率为状态变量，在可测距和考虑弹体姿态噪声条件下提出了相控阵雷达导引头基于UKF的视线重构方案，并通过仿真对重构效果进行了验证。

1相控阵导引头的惯性视线角重构

由视线角定义知LOS的方向向量在弹体系下可表示为

Lb=(1,tanεsecβ,-tanβ)T.

(1)

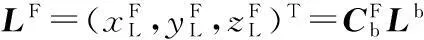
(2)

进而可得惯性视线角为

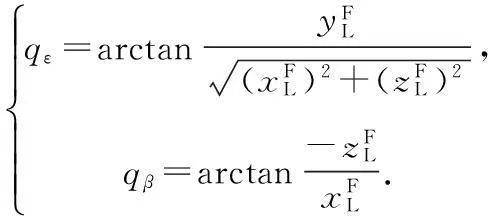
(3)

令Ψ=(ψ,ϑ,γ)T表示弹体姿态角，Ε=(ε,β)T为体视线角，Q=(qε,qβ)T为惯性视线角，并将式(1)～(3)描述的视线角重构过程记作：

Q=G(Ε,Ψ)，

(4)

式(4)即为系统的重构方程。

表1　坐标系定义

2系统建模

2.1系统连续状态方程的建立

为了应用现代控制方法中的非线性滤波估计理论对视线转率进行估计，就需要建立系统的状态空间描述模型，本节将以高低方向为例，建立系统状态空间描述，并做离散化处理。在俯仰平面内弹-目运动方程为[12]

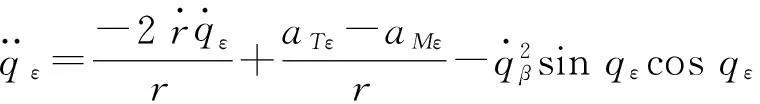
(5)

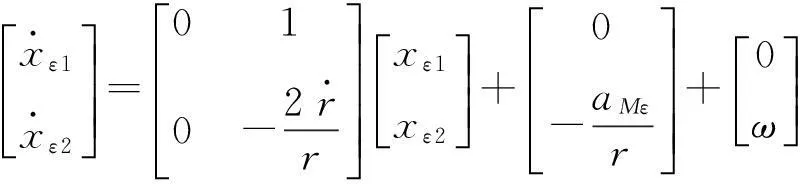
(6)

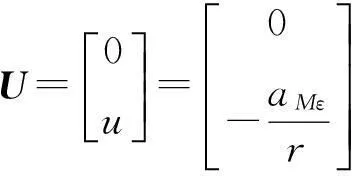
则弹目运动的连续状态空间描述为

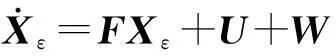
(7).

为了书写方便，在不会引起混乱的情况下，后文将省略Xε等变量表示高低方向的下标，而仅用诸如X形式进行表示。

2.2状态方程的离散化

工程对象一般都是连续系统，但目前实际中多按离散系统滤波方程来计算，因此常需将连续系统离散化。连续系统的离散化实质是：根据连续系统的系统矩阵F计算并简化得到离散系统的转移矩阵Φk+1,k，根据系统的控制输入向量U计算离散化输入Uk，以及根据连续系统噪声方差强度阵Rw计算离散系统噪声方差阵Qk。

根据线性系统理论，式(7)所描述系统的通解为

式中：Φ(t,t0)为式(7)所描述系统的状态转移矩阵。由系统通解容易得到系统的离散描述为

X(tk+1)=Φ(tk+1,tk)X(tk)+

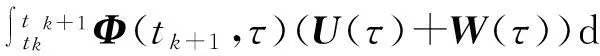
(8)

在一个滤波周期内，过程噪声W的协方差矩阵可看作常矩阵，记为

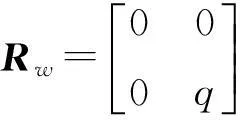
(9)

同样地，在一个滤波周期内将系统矩阵F和系统输入U看作常阵，则式(6)描述的离散化系统状态方程可近似简化为

Xk+1=Φk+1,kXk+Uk+Wk,

(10)

式中：

(11)

(12)

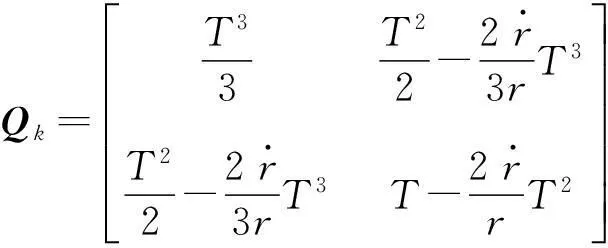
(13)

2.3系统的量测方程

系统的量测方程是视线角重构的逆过程，类比视线角重构过程，容易得到体视线角可表示为

(14)

式中：

(15)

显然，Q，Ψ与Ε之间存在非线性映射关系，将这种映射关系记为

Ε=H(Q,Ψ),

(16)

式(16)就是系统的量测方程。

3UKF惯性视线重构滤波器设计

式(10)和式(16)描述的视线运动是一个典型的量测非线性系统，必须选用非线性滤波方法来实现对视线转率的估计。考虑到无迹卡尔曼滤波(UKF)有较高的估计精度且不需要求解Jacobian/Hessian矩阵[13]，因此本文将基于UKF设计惯性视线重构滤波器。

3.1考虑弹体姿态噪声的增广状态向量

考虑每个量测环节噪声，通过事先对导引头和惯导系统的噪声标定，可得到体视线角量测噪声VE=(νε,νβ)T和弹体姿态角量测噪声VΨ=(νψ,νϑ，νγ)T的统计特性，记它们的协方差分别为RE和RΨ。由于过程噪声Wk与VΨ为乘性噪声，故选择增广状态为：Xa=(qε，qβ，ψ，ϑ，γ)T，其维数为n=5。此时式(16)描述的量测方程可写为

Ε=H(Xa).

(17)

3.2UKF滤波

对于式(10)和式(16)描述的一般形式的非线性系统，UKF滤波过程由以下4个递推步骤完成:

(1) 初始化；

(2) 样点计算；

(3) 时间更新；

(4) 测量更新。

UKF滤波方法是一种常用的非线性系统滤波方法，其递推公式在众多文献中均有详细的介绍[14-15]，本文不再赘述。

4仿真验证

通过一次典型的弹目拦截仿真来验证视线重构滤波器的性能，仿真中不考虑目标机动，导引方法采用比例导引,考虑的量测噪声如表2所示。

表2　噪声模型

表2中弹目距离r的单位为km，时间t单位为s，随机漂移给出的为ξ的标准差，且认为各通道间量测噪声相互独立。仿真中利用微分网络+低通滤波(LF)的传统重构方法与基于UKF的视线重构方法进行对比。图1和图2分别给出了2种方法得到的高低视线角变化率和方位视线角变化率的对比曲线。显然与微分网络+低通滤波(LF)的传统重构方法相比，基于UKF的视线重构滤波器由于考虑了弹目运动模型，在收敛后跟踪精度高，动态延迟小，有很好的跟踪效果；但为了防止UKF发散，需要将初始状态协方差矩阵取的较大，因此UKF需要一段时间才能收敛，且在收敛前估计偏差很大。因此在实际应用时应当将2种方法组合适用，在中后段使用基于UKF的视线重构滤波器输出，而在UKF收敛前使用微分网络+低通滤波的输出作为补充。

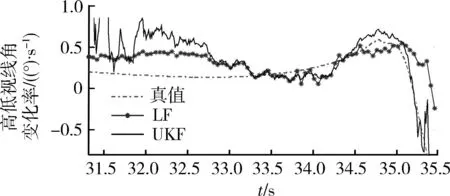
图1　高低视线角变化率重构曲线Fig.1　LOS pitch angle rate reconstruction

图2　方位视线角变化率重构曲线Fig.2　LOS yaw angle rate reconstruction

5结束语

相控阵雷达导引头通常只能直接获取相对于弹体的视线角信息，为了获取比例导引规律所需的惯性视线角速率信息，需要进行视线重构，而如何有效地从重构视线角信息中提取视线转率是重构的难点。本文选取惯性视线角及其变化率为状态变量，在可测距条件下研究了相控阵雷达导引头基于无迹卡尔曼滤波(UKF)的视线重构方案，该方案不仅给出了弹体姿态噪声的处理方法，状态变量维度的降低也大大减小了计算量，仿真结果表明该方法可以有效地改进视线转率的提取精度，但也存在滤波器收敛前估计偏差较大的问题，因此在应用时应当与传统直接微分+低通滤波的方法组合使用。

参考文献：

[1]汤晓云,樊小景，李朝伟.相控阵雷达导引头综述[J].航空兵器，2013(3):25-30.

TANG Xiao-yun,FAN Xiao-jing, LI Chao-wei. Summarization of Phased Array Radar Seeker[J]. Aero Weaponry,2013(3):25-30.

[2]王琪,付书堂.相控阵雷达导引头捷联波束稳定算法研究[J].航空兵器,2011(6):3-5.

WANG Qi,FU Shu-tang. Study on Strapdown Beam Steadying Algorithm of Phased Array Radar Seeker[J].Aero Weaponry,2011(6):3-5.

[3]王嘉鑫,林德福,祁载康，等.全捷联相控阵雷达导引头隔离度寄生回路研究[J].北京理工大学学报,2013,33(11):1124-1129.

WANG Jia-xin,LIN De-fu,QI Zai-kang,et al. Study on Disturbance Rejection Rate Parasitical Loop of Strapdown Phased Array Radar Seeker[J].Transactions of Beijing Institute of Technology, 2013,33(11):1124-1129.

[4]Ekstrand Bertil. Tracking Filters and Models for Seeker Application[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001,37(3):965-977.

[5]Waldmann Jacques. Line-of-Sight Rate Estimation and Linearizing Control of an Imaging Seeker in a Tactical Missile Guided by Proportional Navigation[J]. IEEE Transactions on Control Systems Technology, 2002,10(4):556-567.

[6]Branku Ristic. Tracking a Manoeuvring Target Using Angle-Only Measurements: Algorithms and Performance[J]. Elsevier,Singal Processing,2003, 83(6):1223-1238.

[7]林喆,姚郁,富小薇.捷联成像寻的器视线重构[J].光电工程,2006,33(3):40-43.

LIN Zhe,YAO Yu,FU Xiao-wei. Line-of-Sight Reconstruction for Strap-Down Imaging Seeker[J].Opto-Electronic Engineering, 2006,33(3):40-43.

[8]林喆,姚郁, 马克茂. 捷联成像寻的器ACDKF惯性视线重构[J].红外与激光工程, 2008,37(3):400-405.

LIN Zhe,YAO Yu, MA Ke-mao. ACDKF Inertial LOS Reconstruction Filter with Strapdown Imaging Seeker[J].Infrared and Laser Engineering,2008,37(3):400-405.

[9]薛舜,周军,葛致磊. 捷联导引头目标视线角速率重构方法研究[J].计算机仿真, 2009,26(3):82-86.

XUE Shun,ZHOU Jun,GE Zhi-lei. Line-of-Sight Angle Rate Reconstruction for Strap-down Seeker[J].Computer Simulation, 2009,26(3):82-86.

[10]李璟璟,伊国兴,张迎春. 基于粒子滤波的捷联成像导引头视线角速率估计[J].弹箭与制导学报, 2009,26(2):91-94.

LI Jing-jing,YI Guo-xing,ZHANG Ying-chun. Strapdown Imaging Seeker Los Rate Estimation Based on Particle Filter[J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2009,26(2):91-94.

[11]杨雅君,徐胜利,李晓东，等. 弹载相控阵雷达视线重构研究[J].弹箭与制导学报, 2012,32(5):39-44.

YANG Ya-jun,XU Sheng-li,LI Xiao-dong,et al. The Research on Line-of-Sight Reconstruction Method of Phased-Array Seeker[J]. Journal of Projectiles,Rockets, Missiles and Guidance, 2012,32(5):39-44.

[12]季登高. 基于有限时间范数的末制导系统性能分析[D].哈尔滨：哈尔滨工业大学, 2008:20-22.

JI Deng-gao. Performance Analysis via Finite-Time Norm for Terminal Guidance System[D].Harbin:Harbin Institute of Technology,2008:20-22.

[13]潘泉,杨峰,叶亮，等. 一类非线性滤波器—UKF综述[J]. 控制与决策, 2005,20(5):481-489.

PAN Quan, YANG Feng, YE Liang,et al. T Survey of a Kind of Nonlinear Filters—UKF [J]. Control and Decision, 2005,20(5):481-489.

[14]JULIER S J,UHLMANN J K. A New Approach for Filtering Nonlinear Systems[C]∥Proc of the American Control Conf，Washington Seattle，1995:1628-1632．

[15]WAN E A, UHLMANN J K. The Unscented Kalman Filter for Nonlinear Estimation[C]∥The IEEE Adaptive Systems for Signal Processing，Communications and Control Symposium，2000(10) : 153-158.

Line of Sight Reconstruction for Phased Array Radar Seeker

SHAO Zhen-jie, ZHAO Ming-yuan

(Beijing Institute of Electronic System Engineering,Beijing 100854,China)

Abstract:The method of inertial line of sight (LOS) and inertial LOS rate reconstruction in phasedarray seeker is investigated. Based on unscented Kalman filter(UKF), a novel UKF inertial LOS reconstruction filter is proposed to obtain more precise inertial LOS and LOS rate information. Compared with traditional approach, the new approach avoids differential implement which would induce noise amplification．The results of computer simulations justify the validity of the LOS reconstruction filter, which can be used to improve the accuracy of LOS rate estimation.

Key words:phased-array radar seeker;line of sight(LOS) reconstruction; LOS rate estimation; non-linear filtering; unscented transformation; unscented Kalman filter(UKF)

中图分类号：TJ765.3+31

文献标志码：A

文章编号：1009-086X(2015)-06-0056-05

doi:10.3969/j.issn.1009-086x.2015.06.010

通信地址：100854北京142信箱30分箱E-mail：shaozhenjie_1989@163.com

作者简介：邵真杰(1989-)，男，河南安阳人。硕士生，主要研究方向为导航、制导与控制。

基金项目：有

*收稿日期：2014-12-31；修回日期：2015-01-27