层式通风房间垂直温度分布预测方法*

郇 超，王沣浩，吴小舟，林 章，王志华，王 冠

(1.西安交通大学 能源与动力工程学院, 陕西 西安 710049；2. 西安交通大学 人居环境与建筑工程学院,陕西 西安 710049；3.Building Energy & Environment Technology Research Unit, Division of Building Science and Technology, City Univ of Hong Kong, Hong Kong SAR, China)

层式通风房间垂直温度分布预测方法*

郇 超1，王沣浩2†，吴小舟2，林 章3，王志华1，王 冠2

(1.西安交通大学 能源与动力工程学院, 陕西 西安 710049；2. 西安交通大学 人居环境与建筑工程学院,陕西 西安 710049；3.Building Energy & Environment Technology Research Unit, Division of Building Science and Technology, City Univ of Hong Kong, Hong Kong SAR, China)

基于层式通风房间室内空气流动特性建立了室内垂直温度分布预测模型.该模型将室内空气流动特性与热质平衡方程有机结合，并反映了室内热源强度、墙体辐射及送风参数等边界条件对室内垂直温度分布的影响.通过将模型计算结果与实验数据进行对比分析，发现室内垂直温度预测值与实验数据吻合较好，并在趋势上反映出层式通风房间室内垂直温度的变化特征.因此，本文提出的模型具有较好的预测精度，能够很好地用来指导层式通风系统的实际应用及能耗分析.

层式通风；垂直温度分布；节点模型；能量平衡

目前,中国的建筑能耗约占总能耗的30%[1]，为了减少夏季建筑空调能耗，许多国家都倡导提高夏季空调设定温度以降低空调能耗.然而，落实的情况却差强人意.原因是传统送风方式(混合通风、置换通风)均要求室内气流速度不能过高，若将空调设定温度调高必然会引起室内人员热舒适性的降低(出汗).采用现有系统，纵使室温26 ℃，节能也只有几个百分点, 激励效果有限.个性化送风技术虽节约能耗[2]，但因其在费用、布置和设计方面的困难，至今并未大规模地应用在实际工程中[3].基于此，香港城市大学的林章等学者提出了层式通风系统[4]，保证在低能耗的前提下(亦即在热中性温度较高的条件下)，为室内人员提供良好的空气品质和热舒适环境[5-6].

层式通风系统的典型特征为风口布置在墙体中部，通过空气射流将新鲜的空气直接送入室内人员呼吸区，在呼吸区内形成一个新鲜的空气层.该系统是一种建立在室内气流速度相对较高环境下的高温通风方式，通过加强气流运动(风速+紊流强度)来实现人体热舒适，因此所要求的送风速度相对较大.但是太大的送风速度会导致人体的热不舒适，故其应用范围有一定的限制.林章通过大量研究发现，层式通风可很好地应用于沿送风方向进深不大于9 m，热负荷不大于180 W/m2的房间[7].实际中常规的教室、办公室及小商店等建筑大多在此应用范围内，只要合理设计层式通风系统(送风速度控制在1.3 m/s左右)，则人体周围的气流速度会小于0.8 m/s，计算出的最大PMV介于±0.7之间，PPD<15%[8]，完全能创造出舒适的热环境.

层式通风作为一种新的通风方式，其研究工作仍处于初级阶段.田林等人通过全尺寸实验测试及数值模拟[9-10]对层式通风房间内的环境参数进行了一系列研究，发现垂直方向上室内空气温度存在不均匀性，呼吸区温度明显低于房间其他区域，即层式通风房间内呼吸区与房间上、下部区域存在较大的温度梯度，这要求我们在计算层式通风房间负荷时必须充分考虑其室内温度分布不均匀特性.本文的目的就是要提出层式通风房间室内垂直温度分布预测方法，为层式通风房间负荷及能耗的计算提供理论模型.

1 层式通风房间垂直温度预测方法

室内垂直温度分布预测模型主要有节点模型、区域模型及CFD模型.层式通风房间室内气流组织主要受送风射流、外围护结构内表面及热源产生的羽流综合影响，问题比较复杂，使得区域模型有很多限制.而CFD模型与建筑能量传递耦合模拟时存在许多难以解决的问题，如耦合模拟收敛性、两建筑模型一致性等.节点模型对使用者要求较低，且能够方便地实现与建筑能量传递耦合模拟,Rees和Haves曾建立了较为精细的节点模型来分析置换通风和冷却吊顶房间内的温度分布规律，Wu等人也已建立了分析置换通风及地辐射供暖房间中温度分布的节点模型，并取得了较理想的结果[11].因此本文将采用节点法建立预测层式通风房间温度分布的数学模型.

1.1 节点模型建立

综合考虑热源、人体散热及外墙等因素对房间气流的影响，层式通风房间气流流线简图如图1所示.

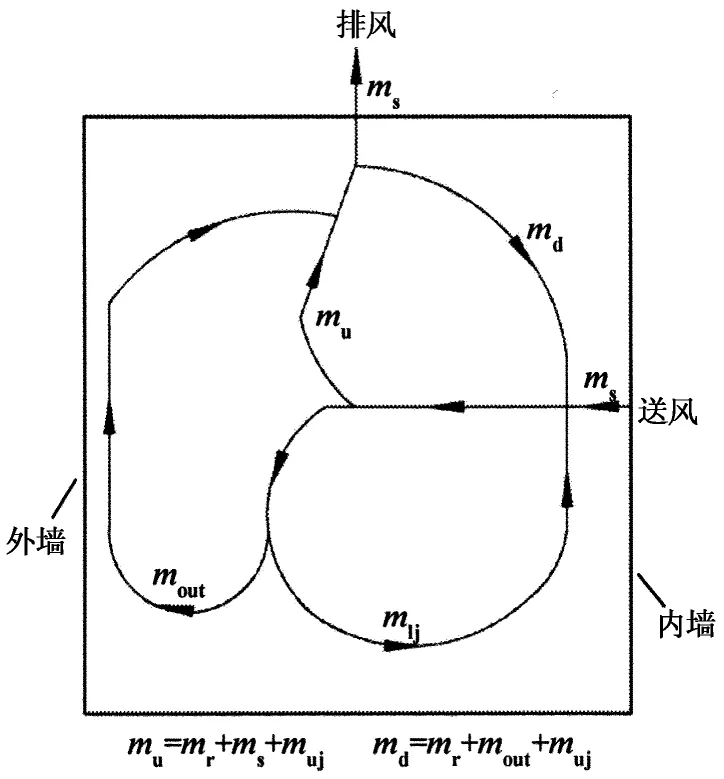
图1 层式通风房间气流示意图

图1中送风射流ms由房间中部送入，并对周围空气产生卷吸作用(卷吸量mj)，射流在到达房间工作区附近时，受到室内办公设备及人体的热作用，诱发产生一部分浮力羽流(mr), 此时，一部分射流卷吸气流muj(由上部空间卷吸)连同热羽流mr和流量为ms的一股气流同时向上运动，这3股气流的总和在图中用mu表示，射流主体中的其余冷气流则向房间下部沉降.下降过程中不断与房间下部区域的高温气流进行热交换，当其温度与房间下部区域整体温度相平衡后，下降气流开始分为2部分：一部分作为射流卷吸作用的补充气流，朝内墙方向流动，然后汇入射流主体，即图中mlj; 另一部分则受到外墙内壁的热作用，进入外墙边界区后成为附壁上升流mout.

本文将层式通风房间沿高度方向分为5个节点，如图2所示，分别为地面面积加权平均温度tf，近地面平均温度tln，房间主体区域体积加权平均温度tn，顶面面积加权平均温度tc及近顶面边界平均温度thn.

此处假设水平面上的温度均匀分布，且呼吸区与房间上部、下部的温度均为线性分布.

1.2 能量平衡构成

根据层式通风房间气流组织特性对各个节点建立质量及能量平衡方程.文中节点模型共包含8个部分的热质平衡，分别为地面、近地面边界、顶面、近顶面边界、外墙内壁、外墙内侧边界、内墙及室内主体区域处的能量守恒.分别对每个部分建立能量平衡方程，然后联立求解所得的热质平衡方程组，便可得到各节点处的温度值.

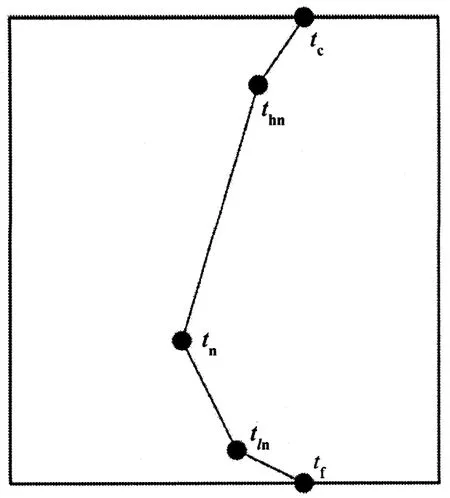
图2 温度节点示意图

1.2.1 地面处能量守恒

地面能量平衡方程为：

Qrf-Qcf+Qhf=0.

(1)

式中：Qrf为房间其余各面对地面的辐射得热；Qcf为地面与近地面空气对流换热量；Qhf为室内热源在地面处的辐射热.

(2)

式中:hcf为地面与地面边界层空气的对流换热系数.

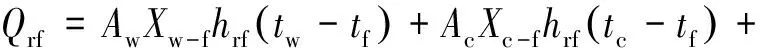
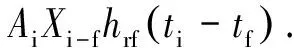
(3)

式中:hrf为地面与房间其他壁面的辐射换热系数，具体取值将在1.3节讨论；Xw-f,Xc-f,Xi-f分别为房间外墙内表面、顶面及内墙壁面对地板的辐射角系数；tw为房间外墙内表面面积加权平均温度；ti为房间内墙面积加权平均温度；tf和tc分别为地板和顶面的面积加权平均温度.

1.2.2 地面边界处能量守恒

地面边界区能量平衡方程为：

Qcf-Qdd=0.

(4)

式中:Qdd为地面边界层空气与下降冷气流进行的热交换量.

(5)

1.2.3 外墙内壁处能量守恒

外墙内壁能量平衡方程为：

Qrw+Qhw-Qcw+Qew=0.

(6)

式中：Qrw为房间其余各面对外墙内壁的辐射得热；Qcw为外墙内壁与近壁面空气的对流换热量；Qhw为室内热源在外墙内壁处的辐射热；Qew是由室外经外墙进入室内的热量.

(7)

式中:tn为房间主体区域体积加权平均温度.

(8)

式中:tew为室外环境温度.

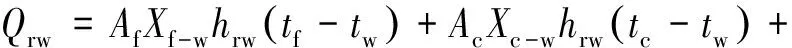
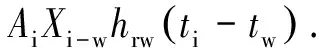
(9)

式中:hcw为外墙内壁与房间其他壁面的辐射换热系数.

1.2.4 壁面边界能量守恒

壁面边界能量平衡方程为：

Qcw-Qln=0.

(10)

式中：Qln为进入壁面边界流体的得热，具体表示为：

(11)

mout=4.0hcwAw/cp.

(12)

式中:tnw为壁面边界层空气温度；mout表示由于外墙的热作用使得由房间下部卷吸进入外墙边界层的空气流量[12]；Aw为外墙内壁面积；cp为空气定压比热容.

1.2.5 顶面能量守恒

天花板处能量平衡方程为：

Qrc-Qcc+Qhc=0.

(13)

式中:Qrc为房间其余各面对顶板面的辐射得热；Qcc为顶面与顶面边界附近空气的对流换热量；Qhc为室内热源在顶面的辐射热.

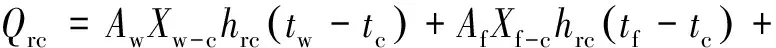
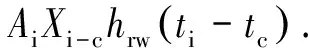
(14)

式中:hrc为顶面与房间其他壁面的辐射换热系数.

(15)

式中:hcc为顶面与顶面边界层空气的对流换热系数，具体取值将在1.3节讨论．

1.2.6 顶面边界层能量守恒

顶面边界处能量平衡方程为：

Qcc-Qec=0.

(16)

式中:Qec为顶面附近空气与进入顶面边界气体的对流换热量.

(17)

式中:mec为房间的排气量.

1.2.7 内壁面能量守恒

内墙壁面上的能量平衡方程为：

Qriw-Qciw+Qhiw=0.

(18)

式中:Qriw为房间其余各面对内墙面的辐射量；Qciw为内墙面与室内空气的对流换热量；Qhiw为室内热源在内墙面的辐射热.

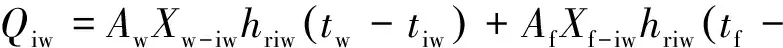
(19)

式中:hriw为房间内壁面与其他壁面间的辐射换热系数.

1.2.8 室内空气主体能量守恒

室内主体区域能量平衡方程为：

Qsn+Qciw+Qhn+Qlnn+Qhnn+Qnw=0.

(20)

式中：Qsn为送风气流与室内空气换热量；Qhn为热源与室内空气换热量；Qlnn为房间下部卷吸气流与室内空气主体换热量；Qhnn为房间上部回流气流与室内空气主体的换热量；Qnw为外墙内壁面边界流体与室内空气的换热量.

(21)

式中:ms为房间送风量.

(22)

式中:mlj为由于射流卷吸作用，由房间下部进入房间主体区域的气流量.

(23)

式中:md为由房间上部区域流入主体区域的空气流.

(24)

1.3 房间垂直温度预测

方程(1)～(24)中包含很多物理量，归类后可分为以下几类：有关房间壁面尺寸的参数Awall，有关壁面温度和换热系数的参数twall,hwall，室内热源强度Qi，节点温度tnodal，送风量ms, 送风温度ts，室外环境温度to以及各部分分流的质量流量M.其中壁面尺寸、辐射角系数、换气次数等量与房间几何尺寸有关.而壁面的换热系数(包括辐射和对流)及各部分分流的流量则可由房间温度、壁面温度及房间几何尺寸等参数来表述.

送风射流的气流卷吸量：

(25)

式(25)由Ricuo和Spalding等通过实验总结得出[13]，其中x为距离送风口的距离，d0为风口的当量直径.

房间地面对流换热系数：

(26)

式(26)由Novoselac等通过对典型办公室中非绝热地面与空气的自然对流换热进行实验分析而得出，适用于典型房间中地面与室内空气自然对流换热[14].

房间壁面对流换热系数：

(27)

式(27)是Awbi等通过实验分析得出的，适用于典型房间中非绝热壁面与室内空气间的自然对流换热[15].

房间顶面对流换热系数：

hcc=0.49ACH0.8.

(28)

由于受热产生的浮升气流及顶部排风作用的影响，房间顶面与近顶面空气的换热属于强制对流，式(28)由Fisher和Pedersen研究得出，适用于典型建筑中顶面强制对流换热[16].

式(26)～式(28)中De为房间边界面的当量直径；ACH为房间换气次数.

房间各边界面上的辐射换热系数为[17-18]：

(29)

式中：ε1,ε2分别为1和2两表面的辐射系数；t1，t2分别为1和2两表面的平均温度；F1为表面1的面积；X1-2为表面1对表面2的辐射角系数.

外墙的传热系数为：

(30)

一般情况下，房间几何尺寸、室内热源强度、送风温度及室外环境温度等参数均可提前确定，将式(25)～(31)代入方程组(1)～(24)后，则原方程组中的未知量只剩各节点温度tnodal和各壁面处温度twall，对方程组进行求解，便可得到层式通风房间中几个高度节点处的温度值.

2 模型计算结果分析

本节建立层式通风房间垂直温度预测模型可行性分析的算例.

2.1 参数选择

为了与实验数据进行对比，将节点模型相关参数选取为课题组之前的实验参数[19].模型所计算房间为西安交通大学建筑环境与设备工程系空调环境实验室(图3)，房间尺寸为3.9 m(长)×2.9 m(宽) ×2.6 m(高)，可根据房间尺寸分别计算出每个面上的辐射角系数.气流由图3中内墙中部(距地面1.3 m)送风口送入，从顶面排风口排出.送风口尺寸为0.21 m(长)×0.17 m(宽)，顶部中间设0.55 m×0.55 m的孔板排风口，与送风口所在墙面相对的左边墙是外墙.室内热源主要集中在房间中部的工作区域(人体和电脑).实验中用尺寸为0.4 m(长)×0.35 m(宽)×1.2 m(高)的铁箱,内置3个

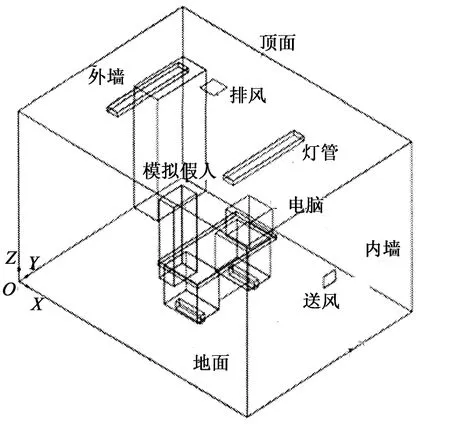
图3 可行性算例房间示意图[9]

功率为25 W的白炽灯来模拟办公室人体坐姿状态时的发热;用尺寸为0.35 m(长) ×0.35 m(宽)×0.35 m(高)的铁箱,内置180 W白炽灯来模拟办公电脑发热.表1列出了房间内热源的选取参数.

表1 房间内热源参数

本文中选择了3种工况进行对比，各工况参数详见表2.

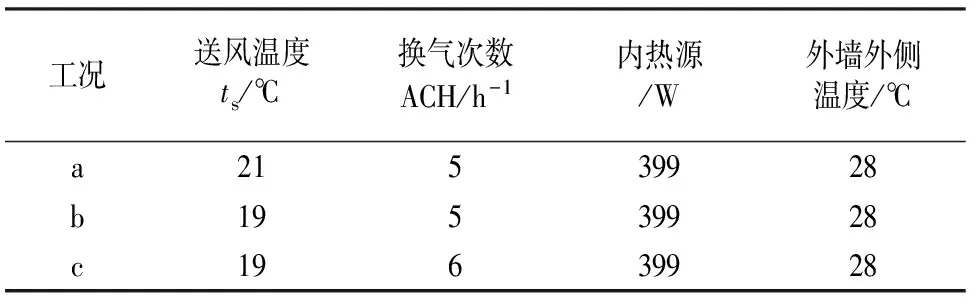
表2 模型计算工况条件

2.2 计算结果对比分析

节点模型中的节点温度tn为房间主体区域的体积加权平均温度，而本文中模型的一个假设条件为：

房间呼吸区与房间上部边界层及下部边界层之间的温度分别呈线性分布，若呼吸层高度的温度为tb，则tb与tn的关系为：

(32)

即

(33)

式(32)(33)中:H为房间高度;H0.1-b为地面边界层至呼吸层之间的垂直高度；thn,tln分别为模型计算得到的房间上、下两边界层处的节点温度.

图4描述了前一节所述的3种工况下，模型计算值与前人实验测试值[19]的结果对比.

由图4可知，工况a情况下人体呼吸高度处模型计算温度与实测值最大温差为0.1 ℃，房间顶部边界层处模型计算温度与实验值温差为0.7 ℃，房间底部边界处计算温度与实验值温差为0.16 ℃，房间各处的温度计算值均与实验数据吻合很好.工况b中随着送风温度的降低，房间高度断面上温度的实测值和模型计算值均明显降低，人体呼吸高度计算温度与实测值最大温差为0.2 ℃，房间顶部边界层处计算温度与实验值温差为1.1 ℃，房间底部边界处计算温度与实验值温差0.24 ℃.工况c中人体呼吸高度模型计算温度与实测值最大温差为0.6 ℃，房间顶部边界层处计算温度与实验值温差为0.1 ℃，房间底部边界处计算温度与实验值温差0.4 ℃.

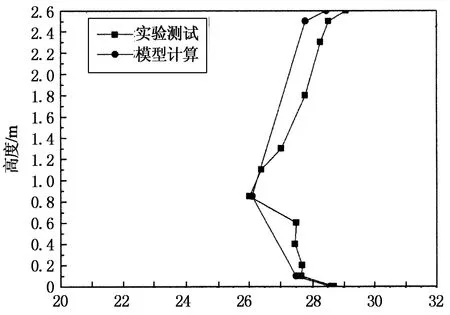
溫度/℃(a)工况a (ts=21 ℃,ACH=5/h-1)

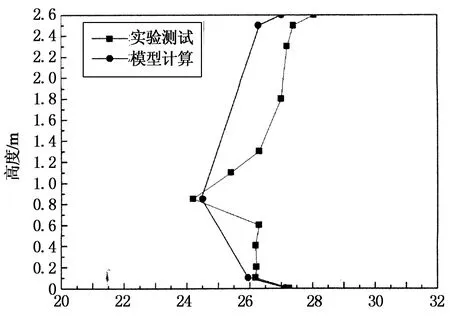
溫度/℃(b)工况b (ts=19 ℃,ACH=5/h-1)

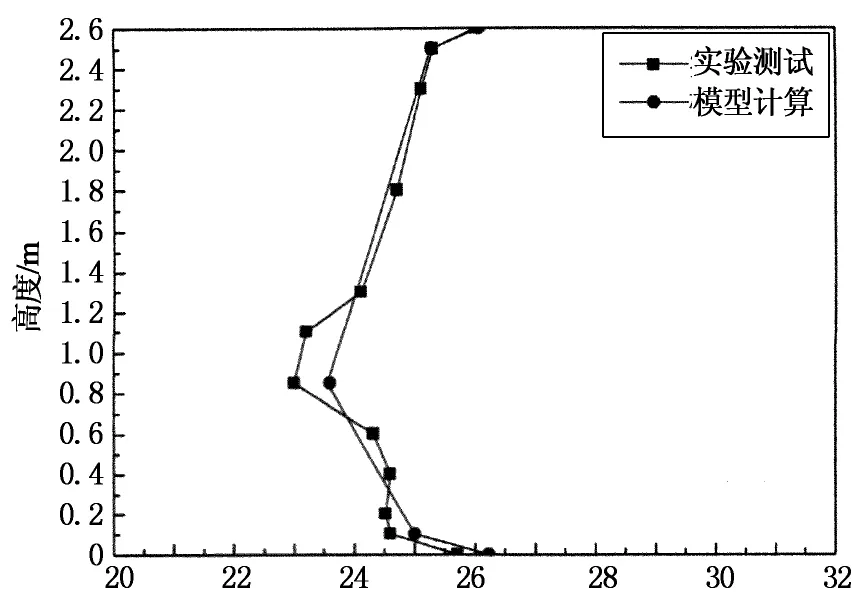
溫度/℃(c)工况c (ts=19 ℃,ACH=6/h-1)

上述3种工况下，节点模型计算结果与实验值基本趋势一致，总体上呈现出了层式通风房间垂直方向上的逆温度梯度特性(即房间上、下部温度高，中部温度低).表3列出了分别在模型和实验条件下，呼吸层温度值tb和房间下部区域(0.1～0.9 m)垂直温差Δt0.1-0.9.分析发现，3种工况下模型计算出的呼吸层温度与实测值吻合得很好，最大误差只有0.6 ℃；而2种方式得出的房间下部垂直温差差别微小，最大误差为0.44 ℃，实际情况中的静坐工作人员正是处于此区域，3种工况下计算和实测的Δt0.1-0.9均小于3 ℃，满足ASHRAE 55—2010中关于工作区垂直温差的热舒适要求.

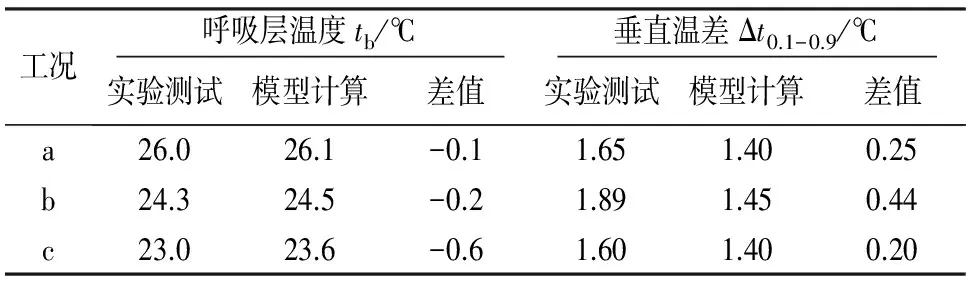
表3 模型和实验下呼吸层温度及房间下部区域垂直温差

表4是通过节点模型和实验数据得到的房间热分布系数m，其具体表达式为：

(34)

表4中的模型计算值与实验结果吻合较好，2种方式所得结果均反映出随着送风温度的下降和换气次数的增加，层式通风房间热分布系数有减小的趋势.而模型计算结果相比实验结果略微偏高，这是由于模型简化处理中，将房间顶部的热源(灯具)并入了工作区内造成的，相应的模型调整将在后续研究中完成.

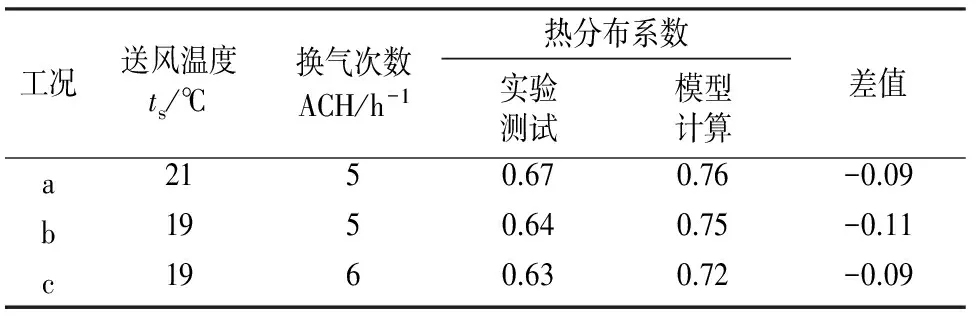
表4 模型和实验下的房间热分布系数

上述研究结果表明，层式通风房间节点模型的计算结果与实测数据保持了较好的一致性，为今后用该模型来指导层式通风的实际应用创造了可能性.实际工程中可采用该数学模型，快速计算出不同边界条件下层式通风房间的工作区温度、人体头部和脚部的温差以及除热通风效率等参数，来对系统的舒适性进行初步预测，避免了因采用CFD技术所占用的冗长计算时间.此外，还可以利用该数学模型，将房间内一些所需求的温度值输入模型，反推出房间边界条件的选取参数，促进层式通风系统在实际应用中快速设计及选型.

3 结 论

本文基于层式通风房间室内空气流动特性及热质平衡理论，建立了合理的室内垂直温度分布预测模型.模型计算结果与实验数据吻合较好，并在趋势上反映出层式通风房间室内垂直温度的变化特征.因此，该模型能较好地预测层式通风房间室内垂直温度分布，为今后开展有关层式通风房间能耗负荷的研究工作提供了理论支撑，也为实际工程中层式通风系统的设计选型提供了工具.

[1] 杨昌智,张清琳,杨菊菊.定温控制空调系统的舒适性及节能性分析[J].湖南大学学报：自然科学版, 2012,39(5): 18-22.

YANG Chang-zhi, ZHANG Qing-lin, YANG Ju-ju. Analysis of comfort and energy-consumption on temperature control air-conditioning system[J]. Journal of Hunan University: Natural Sciences, 2012, 39(5): 18-22. (In Chinese)

[2] 龚光彩,谢赛男,吴京龙.座椅送风大空间湿度分布模拟[J].湖南大学学报:自然科学版, 2008,35(7): 21-24.

GONG Guang-cai, XIE Sai-nan, WU Jing-long. Humidity distribution simulation of chair ventilation in large space[J]. Journal of Hunan University: Natural Sciences, 2008,35(7):21-24. (In Chinese)

[3] 邵晓亮, 马晓钧，李先庭.利用“N”个送风口同时保障大于“N”个位置个性化温度需求的方法研究[J]. 建筑科学,2012,28(S2):52-57.

SHAO Xiao-liang, MA Xiao-jun, LI Xian-ting. Research on guaranteeing the personalized temperature requirement at more than N locations just by N air supply inlets [J]. Buinding Science, 2012,28(S2):52-57.(In Chinese)

[4] LIN Z, CHOW T T, TSANG C F,etal. Stratum ventilation—a potential solution to elevated indoor temperatures[J]. Building and Environment, 2009, 44 (11): 2256-2269.

[5] LIN Z, LEE C K, FONG K F,etal. Comparison of annual energy performances with different ventilation methods for cooling[J]. Energy Build, 2011, 43(1):130-136.

[6] LIN Z, LEE C K, FONG K F,etal. Comparison of annual energy performances with different ventilation methods for temperature and humidity control[J]. Energy Build, 2011, 43(12):3599-3608.

[7] LIN Z, YAO T, CHOW T T,etal. Performance evaluation and design guidelines for stratum ventilation[J].Building and Environment, 2011, 46(11): 2267-2279.

[8] LIN Zhang. Effective draft temperature for evaluating the performance of stratum ventilation[J]. Building and Environment, 2011, 46(9): 1843 -1850.

[9] TIAN Lin, LIN Zhang, WANG Qiu-wang. Experimental investigation of thermal and ventilation performances of stratum ventilation[J]. Building and Environment, 2011, 46(6): 1309-1320.

[10]TIAN Lin, LIN Zhang, WANG Qiu-wang. Comparison of gaseous contaminant diffusion under stratum ventilation and under displacement ventilation[J]. Building and Environment, 2010, 45 (9):2035-2046.

[11]WU X Z, OLESEN B W, FANG L E I,etal. A nodal model to predict vertical temperature distribution in a room with floor heating and displacement ventilation[J]. Building and Environment, 2013, 59: 626-634.

[12]高军. 建筑空间热分层理论及应用研究[D].哈尔滨：哈尔滨工业大学市政环境工程学院，2007：139-142.

GAO Jun. Research of the theory of thermal stratification in buildings and its applications[D]. Harbin: School of Municipal and Environmental Engineering, Harbin Institute of Technology, 2007: 139- 142. (In Chinese)

[13]RICUO F P, SPALDING D B. Measurement of entrainment by axisymmetrical turbulent jets[J]. Journal of Fluid Mechanics, 1961,11(1):21-32.

[14]NOVOSELAC A, BURLEY B J, SREBRIC J. Development of new and validation of existing convection correlations for rooms with displacement ventilation systems[J]. Energy and Buildings, 2006, 38(3): 163-173.

[15]AWBI H B, HATTON A. Natural convection from heated room surfaces[J]. Energy and Buildings, 1999，30(3):233-244.

[16]FISHER D E, PEDERSEN C O. Convective heat transfer in building energy and thermal load calculations[J]. ASHRAE Transactions, 1997,103(2):137-148.

[17]OLESEN B W, BONNEFOI F, MICHEL E,etal. Heat exchange coefficient between floor surface and space by floor cooling—theory or a question of definition[C]//ASHRAE Transactions Symposia，2000: 684-694.

[18]CAUSONE F, CORGNATI S P, FILIPPI M,etal. Experimental evaluation of heat transfer coefficients between radiant ceiling and room[J]. Energy and Buildings, 2009, 41(6):622-628.

[19]刘晓东,严彩球，李远斌, 等. 层式通风室内气流组织特性试验研究[J]. 制冷与空调，2009,9(2):57-60.

LIU Xiao-dong, YAN Cai-qiu, LI Yuan-bin,etal. Experimental study of the air distribution characteristics in room of stratum ventilation[J]. Refrigeration and Air-Conditioning, 2009,9(2):57-60.(In Chinese)

A Method to Predict Vertical Temperature Distribution in a Stratum-ventilated Environment

HUAN Chao1,WANG Feng-hao2†，WU Xiao-zhou2,LIN Zhang3,WANG Zhi-hua1,WANG Guan2

(1. School of Energy and Power Engineering, Xi’an Jiaotong Univ, Xi’an,Shaanxi 710049, China;2. School of Human Settlements and Civil Engineering, Xi’an Jiaotong Univ, Xi’an,Shaanxi 710049, China;3. Building Energy & Environment Technology Research Unit, Division of Building Science and Technology, City Univ of Hong Kong, Hong Kong SAR, China)

As a new energy-saving air supply mode, stratum ventilation system has not been widely applied due to inadequate theoretical support. A mathematical model based on the characteristics of the indoor air flow was established to predict the vertical temperature profile in a stratum ventilated room. By combining the characteristics of indoor air flow with mass and energy equilibrium equations, this model gave the quantitative relationship between indoor vertical temperatures and boundary conditions such as heat source, enclosure radiation and supply air parameters. A comparative study shows that the predictions of this model fit the experiment values well. The model can represent the practical vertical temperature profiles in a stratum ventilated room. The analyses indicate that this proposed model has acceptable accuracy and can be used for practical engineering designs and energy consumption analysis.

stratum ventilation; vertical temperature distribution; nodal model; energy balance

1674-2974(2015)05-0134-07

2014-05-23

国家自然科学基金资助项目(51178407)，National Natural Science Foundation of China(51178407)

郇 超(1985-)，男，甘肃酒泉人，西安交通大学博士研究生

†通讯联系人，E-mail: fhwang@mail.xjtu.edu.cn

TU831.8

A