地震作用下节理岩质边坡的动力稳定性分析

王泉伟， 杜朋召， 张涛， 刘建磊

(黄河勘测规划设计有限公司，河南 郑州 450003)



地震作用下节理岩质边坡的动力稳定性分析

王泉伟， 杜朋召， 张涛， 刘建磊

(黄河勘测规划设计有限公司，河南 郑州 450003)

摘要：基于离散数学的思想，将边坡离散为众多子区域，利用离散元强度折减法，以子区域特征点的位移时程曲线是否收敛作为岩体的失稳判据，研究节理岩质边坡的动力稳定性.通过分析边坡的动力响应规律，验证了由该方法确定的边坡滑面位置及安全系数是合理的.在此基础上，以某大型节理岩质边坡为例，分析了地震作用下边坡的变形破坏特征.计算结果表明，边坡的变形破坏存在浅表层动力效应，该效应在汶川震区边坡震害中多有体现.通过分析边坡浅表层动力效应的产生机理，为节理岩质边坡的防护提供一定的参考.

关键词：边坡工程；节理岩质边坡；地震；动力稳定性；离散元；强度折减法

近年来，随着我国西部大开发战略的实施，西部水利水电工程的数目越来越多，规模越来越大.但西部地区区域地质构造复杂,活动断裂发育，是高烈度地震的多发区域，区内存在11个8.5级、45个8级、208个7.5级和478个7级潜在震源区[1].处于西部高山峡谷中的水利水电工程岩质边坡，具有坡体高陡、坡型多变、岩体结构复杂、节理裂隙发育等特点[2].在地震作用下，节理岩质边坡的变形破坏较天然状况时更为严重，对水利水电工程的安全运营威胁更大，已成为亟待解决的重大工程问题.

郑颖人等[3]提出利用有限元强度折减法，对岩土体折减后的抗拉、抗剪强度进行动力计算，根据关键点位移曲线的变化趋势来分析边坡稳定性；李海波等[4]在研究地震作用下顺层岩质边坡稳定性时，结合离散元强度折减法，以关键点位移时程曲线是否收敛为依据判断边坡的临界状态，确定边坡动力稳定系数.但采用有限元分析时，折减系数及关键点位移曲线的拐点不易判断；对于节理岩质边坡，地震作用下边坡的破坏范围及滑动面的位置仍无法准确确定.为此，本文尝试基于离散数学的思想，将边坡离散为众多小的子区域，以每个子区域的形心或特征点的位移时程曲线作为研究对象，通过分析地震作用下各子区域的变形特征，来确定边坡整体的变形破坏规律.同时，将强度折减法与离散元动力计算相结合，以位移时程曲线是否收敛作为岩体的失稳判据，通过分析不同折减系数下各子区域特征点的时程曲线，来确定边坡的变形破坏范围及动力安全系数.运用上述方法对某大型节理岩质边坡进行动力分析，总结地震作用下节理岩质边坡的变形破坏机理.

1方法分析

1.1　计算模型及参数选取

1.1.1岩体模型

岩体模型取水平宽度为100 m，高度为80 m.其中，坡高为50 m、坡度为45°.岩体中取一组节理，节理倾角为30°.将模型部分离散为边长为2 m的子区域，如图1所示.将模型顶部第1排子区域记为监测线L1，监测线靠近坡面的第1个点为L11.

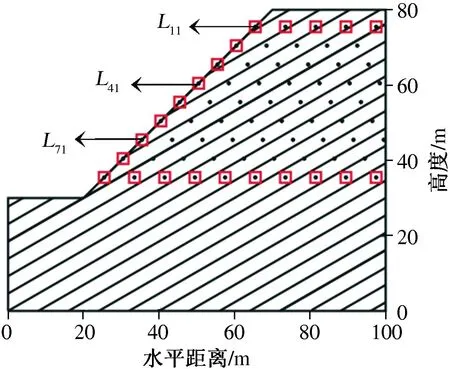
图1　边坡模型及测点位置

1.1.2计算模型及参数

数值模拟中，岩石材料采用理想弹塑性模型，屈服准则采用Mohr-Coulomb强度准则；结构面选用面接触的Coulomb滑动模型.模型岩石材料和结构面的物理力学指标分别见表1和表2.

表1　模型岩石的物理力学参数

表2　模型结构面的物理力学参数

1.1.3地震波输入

在模型底面施加余弦剪切应力波，其加速度时程方程为

a=λcos(2πft).

式中：振幅λ取1.25 m/s2，相当于Ⅶ度区的地震加速度振幅；频率f取4 Hz，地震持续时间t取1 s，计算时间为2 s.

模拟选用三角形单元，网格尺寸取1 m.采用局部阻尼，阻尼系数α为0.125.模型左右两边选用自由边界，模型底部施加黏性边界.

1.2　计算结果分析

1.2.1强度折减前

对模型进行动力计算，得到各监测点的位移时程曲线，如图2所示.

图2　强度折减前各测点的位移时程曲线

不同高度距坡面距离相同点的位移如图3所示.由于模型影响深度有限，边坡深部的检测点对结果的意义不大，故每排选取5~6个代表性监测点进行研究.

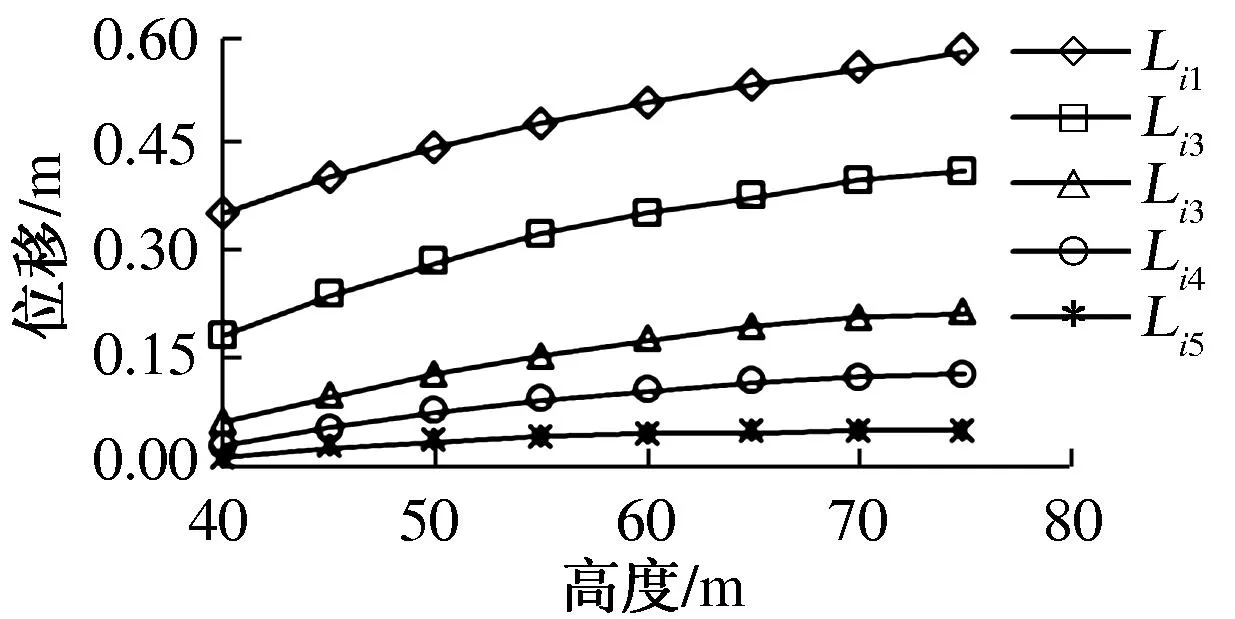
图3　不同高度距坡面距离相同测点的位移

从图2和图3中可以看出：

1)在地震作用期间，模型各监测点位移曲线上下波动，质点在剪切应力波作用下左右振荡；

2)地震作用结束后，模型各监测点位移保持恒定，变形不再增加，表明边坡整体处于稳定状态；

3)地震作用结束后，模型同一监测线上由内向外各监测点位移逐渐增加，边坡水平放大效应显著，且放大效应主要集中在坡面附近一定范围内；

4)地震作用结束后，模型中距坡面距离相同的各监测点的位移随高程的增加而增大，高程放大效应明显.

上述计算结果与地震作用下边坡的变形规律基本一致，由此表明模型计算结果是合理、正确的.

1.2.2强度折减后

对模型岩体参数进行等比例折减，当折减系数为1.16时，通过动力计算，得到模型中各监测点的位移时程曲线，如图4所示.折减后边坡变形破坏区域，如图5所示.

图4　强度折减后各监测点的位移时程曲线

图5　强度折减后边坡的失稳破坏区域示意

从图4和图5中可以看出：

1)模型岩体参数折减后，在地震作用下，模型部分监测点位移时程曲线不收敛，岩体位移随时间持续增加，表明岩体已失稳破坏；

2)模型监测线L1中不收敛曲线数目为3，监测线L2、L3、L4、L5的数目分别为2、2、1和1，由此可以确定边坡的变形破坏范围及滑动面；

3)岩体折减系数为1.16时，边坡在地震作用下发生整体失稳破坏，表明模型动力安全系数为1.16.

2工程实例

以黄河上游某大型水利水电工程边坡为研究对象，边坡位于电站右岸坝前石门沟上游—双树沟范围内，距大坝500~1 300 m.坝址区为典型的深切“V”字型河谷地貌，蓄水前边坡地段水面高程约为2 250 m，坡顶平台前缘高程约为2 950 m，相对高差700 m.边坡上陡下缓，自然坡度为40°~50°.边坡基岩出露，主要为中生代印支期花岗岩，由表及里依次分为散体带、碎裂带、块裂带和原岩.

由于复杂的地质构造背景和河谷演化历史，两岸岩体浅表层改造强烈，边坡区域存在大量的结构面.其中Ⅱ、Ⅲ级断裂结构面共10条，延伸长度约50~200 m，如LF1、Hf104等；Ⅳ、Ⅴ级结构面数目众多，分布广泛，主要有4组对边坡岩体变形破坏起控制作用的节理、裂隙，其在边坡岩体中的分布如图6所示.

实测地应力资料表明，坝址区地应力在400 m深度范围内为20~30 MPa，在河床部位可达50 MPa以上，为高地应力区.

坝址区地震基本烈度为Ⅶ度，设计地震烈度为Ⅷ度，100年超越概率2%的基岩地震动峰值加速度为0.23 g.

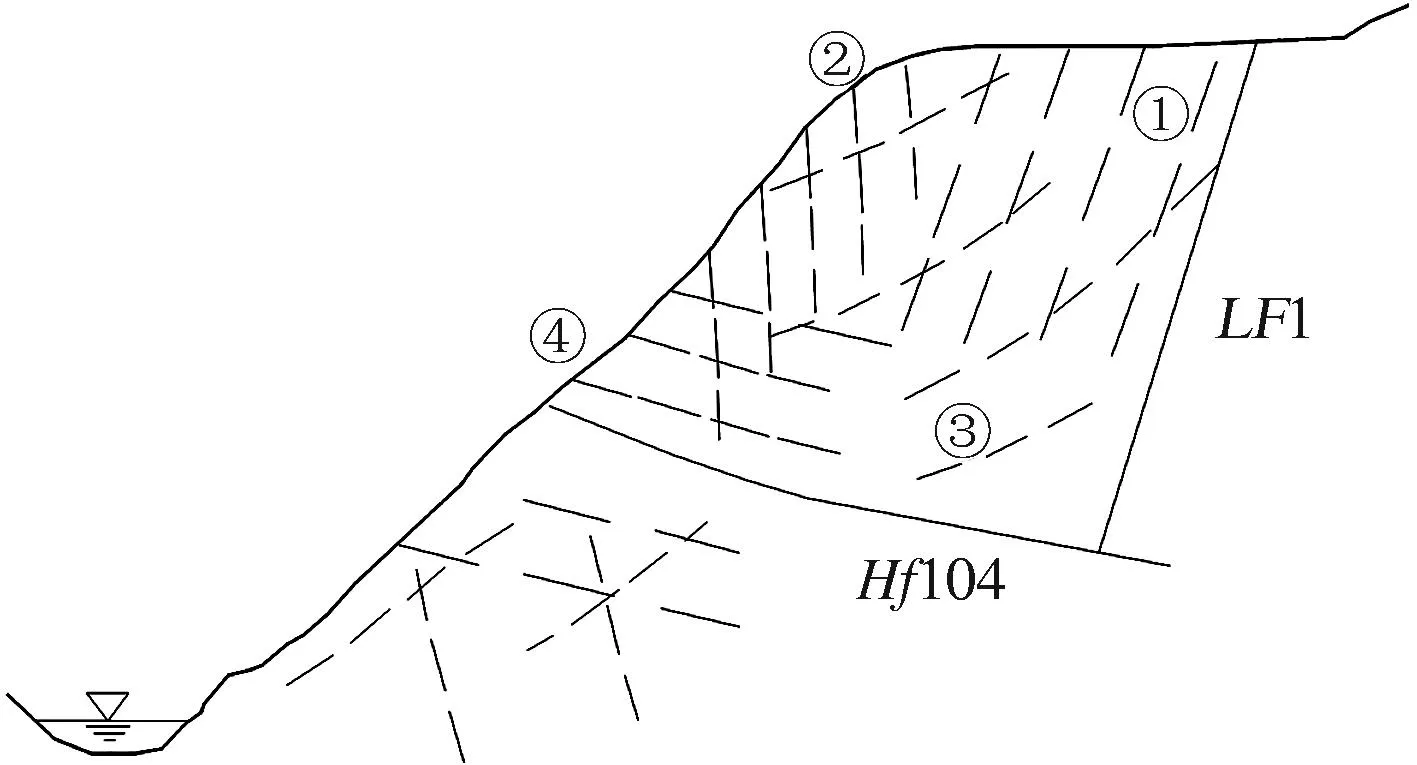
图6　各级结构面在边坡岩体中的分布

3边坡动力分析

3.1　计算模型

对于边坡Ⅱ、Ⅲ级断裂结构面，在模型中直接模拟；对于Ⅳ、Ⅴ级随机结构面，在模型中采用网络模拟.边坡结构面网络模拟结果如图7所示[5].

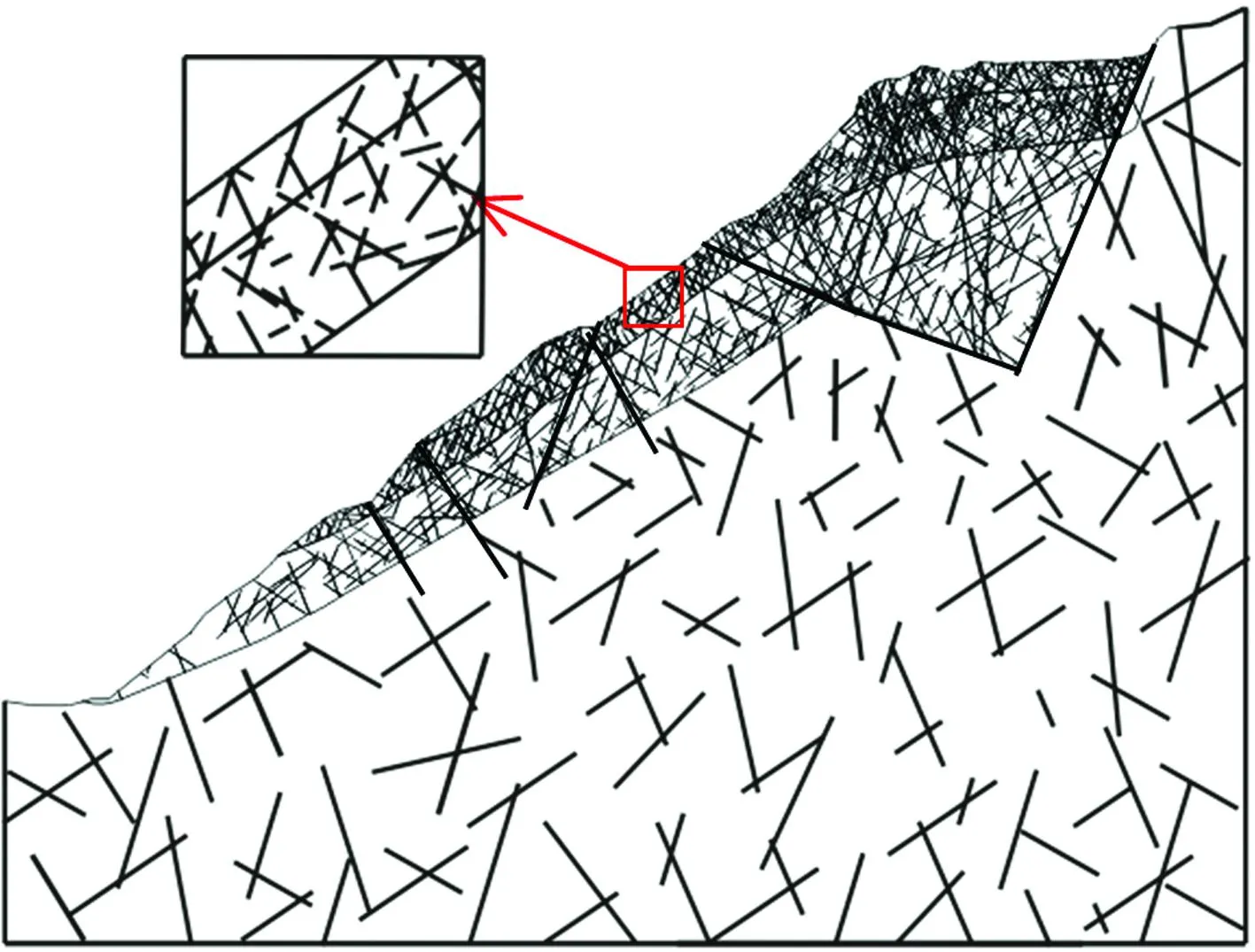
图7　结构面的网络模型

3.2　力学参数

综合现场及室内试验，并结合相关工程经验，边坡岩体及结构面的力学参数取值见表3和表4.

表3　岩体的物理力学参数

表4　结构面的力学参数

3.3　地震波输入

对边坡进行动力计算时，模型左右施加自由场边界，底部施加黏性边界；选取美国EL CENTRO地震波作为动力输入条件，并对其进行低通滤波和基线校正处理，以使速度与位移变数在最终时刻归零或基本归零，生成合理的加速度波形，如图8所示.

由于EL CENTRO地震波的能量主要集中在前30 s，30 s后地震加速度基本趋于0 g.因此，边坡动力计算时，地震持续时间取30 s.

图8　处理后的EL CENTRO波加速度时程曲线

3.4　结果分析

边坡的动力计算结果显示，在地震作用的初始阶段，边坡内部的潜在滑动面尚未贯通，边坡的变形破坏以表层岩体局部掉块、垮塌为主；随着地震持续时间的增加，岩体内部的结构面逐渐张开、延伸，最终形成贯通滑面，导致边坡产生滑坡或崩塌破坏；边坡的变形破坏具有渐进性.

通过分析边坡各子区域关键点的位移时程曲线，得到边坡在地震作用下的变形破坏区域，如图9所示.

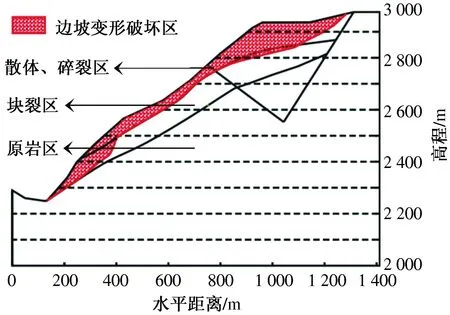
图9　地震作用下边坡的变形破坏区域示意

从图9中可以看出，地震作用30 s后，边坡变形破坏区域主要集中在边坡表层的散体区和碎裂区，即边坡的浅表层区域.文中将这种现象称为地震作用下节理岩质边坡变形破坏的浅表层动力效应，该现象在汶川震区边坡震害中多有体现[6].

地震作用下，节理岩质边坡浅表层动力效应机理主要包括以下3个方面：

1)边坡内部不存在显著的软弱面，即不存在确定性的滑动面.因此，在地震作用下，边坡岩体难以产生沿某一贯通滑面的整体动力失稳，岩体的变形破坏是一个随地震作用而渐进损伤的过程.

2)边坡浅表层岩体内节理、裂隙发育，完整性差，而边坡内部岩体节理、裂缝的发育程度较低，完整性较好；由于地震波在完整岩石内传播速度快，在破碎岩体中传播速度减慢，导致边坡浅表层与坡体内部岩体间的不协调运动，从而在边坡浅表层岩体中产生往复的剥离拉应力.在这种力的作用下，边坡浅表层岩体损伤加剧，岩体内部的结构面逐渐张开、延伸，最后形成贯通性滑动面，导致边坡浅表层岩体失稳破坏.

3)边坡浅表层破碎岩体的自振频率相对于内部完整岩体较小，而自然地震的地震波能量主要集中在低频范围内，因此，边坡浅表层岩体的共振效应相对内部岩体更加强烈.同时，边坡浅表层岩体强度相对较低，由此导致边坡浅表层成为地震作用下岩体变形破坏的主要区域.

4结语

通过分析边坡的动力响应规律可知，将边坡离散为众多子区域，以子区域特征点的位移时程曲线是否收敛作为岩体的失稳判据，并结合离散元强度折减法，能够准确确定边坡的破坏范围及滑面位置，得到合理的边坡动力安全系数.

某大型节理岩质边坡的动力分析结果显示：在地震作用下，边坡的变形破坏具有显著的渐进性特征；随地震持续时间的增加，岩体内部的结构面逐渐张开、延伸，最终形成贯通滑面，导致边坡产生滑坡或崩塌破坏.

地震作用下，节理岩质边坡的变形破坏存在浅表层动力效应，该现象在汶川震区边坡震害中多有体现，文中分析了边坡浅表层动力效应的机理，为节理岩质边坡的防护提供一定参考.

参考文献

[1]胡聿贤．地震工程学:水利水电工程卷[M]．北京：地震出版社，2006．

[2]黄润秋．岩石高边坡发育的动力过程及其稳定性控制[J]．岩石力学与工程学报，2008，27(8)：1525-1544．

[3]郑颖人,叶海林,黄润秋，等．边坡地震稳定性分析探讨[J]．地震工程与工程振动，2010，30(2)：173-180．

[4]李海波,肖克强,刘亚群．地震荷载作用下顺层岩质边坡安全系数分析[J]．岩石力学与工程学报，2007，26(12)：2385-2394．

[5]杜朋召,刘建,韩志强，等．基于复杂结构精细描述的岩质高边坡稳定性分析[J]．岩土力学，2013，34(S1)：393-398．

[6]蒋良潍,姚令侃,胡志旭，等．地震扰动下边坡的浅表动力效应与锚固控制机理试验研究[J]．四川大学学报(工程科学版)，2010，42(5)：164-174．

(责任编辑:杜明侠)

Analysis on Dynamic Stability of Jointed Rock Slope under Earthquake Action

WANG Quanwei, DU Pengzhao, ZHANG Tao, LIU JianLei

(Yellow River Engineering Consulting Co., Ltd., Zhengzhou 450003, China)

Abstract:Based on discrete mathematics, the slope is dispersed lots of sub-regions. For researching dynamic stability of jointed rock slope, strength reduction method based on DEM is applied. The equilibrium condition is estimated based on convergence property of key points′ displacement-time curve in every sub-region. Through analyzing the laws of the slope′s seismic response, the results show that the sliding surface position and the safety factor determined by the method are proved reasonable. To analysis the characteristics of slope deformation and failure, the method above is applied to the stability analysis of a jointed rock slope under earthquake action. The study shows that the deformation and failure of slope has a shallow surface dynamic effect, which is reflected in many slope disasters of Wenchuan earthquake region. Consequently, the analysis on the mechanism of slope′s shallow surface dynamic effect can provide a reference for the prevention of jointed rock slope.

Keywords:slope engineering; jointed rock slope; earthquake; dynamic stability; discrete elements; strength reduction method

文献标识码：A

文章编号：1002-5634(2015)06-0063-05

中图分类号：P642

DOI:10.3969/j.issn.1002-5634.2015.06.016

作者简介：王泉伟(1972—)，男,河南西峡人，高级工程师，主要从事水文地质与工程地质勘察方面的研究.

收稿日期:2015-08-20