汽轮机振动信号的最小方差谱估计算法*
2015-01-01石现峰
张 峰,尹 丽,石现峰
(西安工业大学 电子信息工程学院,西安710021)
在汽轮机振动信号谱估计中,最常采用的方法就是以周期图法为代表的经典谱估计的各种算法[1].由于汽轮机振动信号并非纯粹的平稳随机过程,利用经典谱估计算法分析汽轮机振动信号的功率谱有一定局限性,会产生谱估计质量不高的问题,影响后续处理[2].基于经典算法的局限性,又提出了现代谱估计算法[3],AR模型算法就是其中之一,不仅克服了经典谱估计算法的局限性而且使方差性能与分辨力性能得到很大的改善[4].拥有很好的方差性能和分辨力性能可进一步提高振动信号频谱分析的精度和准确性。由于AR模型算法的方差性能还没有达到很好的效果,文章中引入了最小方差谱估计算法[5],其是在AR模型基础上的改进,在基本保证分辨力性能的基础上进一步提高了方差性能[6].在最小方差谱估计算法原理的基础上,对工业现场实测振动信号进行了功率谱仿真与分析,对比了周期图法、Welch算法以及AR模型的仿真结果.
1 最小方差谱估计算法
经典谱估计算法应用存在局限,在谱估计领域逐渐引入了现代谱估计算法,AR模型就是其中一种.AR模型算法的基本思路是把将白噪声信号通过AR模型系统,采用Burg算法求出其模型系数[7].最小方差功率谱估计 (Minimum-Variance Spectral Estimation,MVSE)是在 AR功率谱估计的基础上的改进,提高了方差性能,但是分辨力性能会有一定的牺牲[8].现对最小方差谱估计算法与AR模型算法的关系进行讨论.
AR模型谱估计系数求取按式(1)计算为



2 汽轮机振动信号分析
2.1 汽轮机振动信号的时域图形
文中引入的谱估计算法主要用来处理振动信号.便于算法研究的针对性,对工业现场汽轮机振动信号进行了采集.所用的振动传感器为美国Bentley公司的电涡流式传感器,汽轮机转轴理想情况转速为3 000r·min-1,即转动频率为50Hz.按照32倍频采样频率(即采样频率fs=50×32=1 600Hz)进行信号采样,采样点数为128点,采样时域图如图1所示.

图1 实测的振动信号时域波形Fig.1 Waveform of sampled vibration signal in time domain
从图1中可看出,单纯从时域,很难对振动信号的特征进行准确分析,难以发现、定位故障信息,需要借助功率谱估计算法作为故障提取与分析的工具.功率谱估计算法主要研究随机信号在频域中的各种特征,目的是根据有限数据在频域内提取被淹没在噪声中的有用信号.
2.2 经典谱估计算法及其局限
为了突出最小方差谱估计算法在汽轮机振动信号分析中存在的优势,论文列出了传统也是应用最多的谱估计算法周期图法及其一种改进算法的仿真结果.图2和图3分别为基于Matlab使用周期图法和 Welch算法[11](数据分段长度为64,段与段之间有50%重叠,数据的加窗类型为矩形窗)对图1所示信号进行谱估计所绘制出的功率谱图.

图2 周期图法谱图Fig.2 Spectrum based on the periodogram method

图3 Welch算法谱图Fig.3 Spectrum based on the welch method
由图2可看出,周期图法得到的谱图分辨力性能较好,谱峰较尖锐,但方差性能差,谱图起伏很大,难以保证谱分析的准确性,且对噪声的容忍能力差.
同时,由图3可看出,Welch算法对周期图法的方差性能进行了改进,减小了谱图的起伏,但是分辨力性能下降严重,甚至无法准确定位信号的各谐波分量.
可见,经典算法存在的方差和分辨力性能的矛盾,在汽轮机振动信号分析中应用有局限性,尤其在因实时性、处理速度等因素限制而无法采集与处理较长振动信号数据的情况下,算法局限性尤为明显[12].产生这一问题的本质原因在于经典谱估计算法存在对时域信号进行加窗的过程,造成频谱泄露,影响了谱估计的效果.数据采样点数越少,相当于加窗长度越短,则频谱泄露效应越明显[13].
2.3 最小方差谱估计算法的实现
以上述算法分析为基础,汽轮机振动信号最小方差谱估计算法过程为
①对采集到的振动信号进行去直流成份处理.若信号含有直流分量,会使信号在进行功率谱估计时,0频率处出现一个很大的谱峰,影响其他频率成分的频谱曲线,从而影响谱估计效果,所以要对其进行去直流处理[14].
②确定谱估计最佳阶次.文中将AIC准则应用到最佳阶次的确定中.
③根据确定的最佳阶次,根据Burg算法计算出 AR模型谱估计的参数ap(1),…,ap(p).
④根据最小方差谱估计参数与AR模型参数间的关系即式(4),确定最小方差谱估计的参数值.
⑤ 以计算出的最小方差谱估计算法参数为基础,计算出振动信号的功率谱,并进行归一化处理;
⑥将振动信号的归一化功率谱转换为对数谱,并绘制功率谱图.
2.4 最优阶次的确定方法
在利用最小方差谱估计算法对汽轮机振动信号进行功率谱分析时,模型阶次p的确定是一个重要的问题.阶次p过低,会导致谱图过于平滑,降低分辨力;而阶次p过高,会产生虚假的谱峰,同时会大大增加计算量.所以算法在实际应用中,存在一个最佳的阶次,这一最佳阶次可通过不同的准则进行确定.最小方差是在AR模型基础上的改进,可以借用AR模型最佳阶次的确定方法,将其与最佳阶次确定方法中的AIC准则相结合.其定义为

按照信息论准则,即式(6),结合Burg算法[9]计算出预测误差功率σ2p,编写程序计算并绘制出AIC(p)曲线,以便于最佳模型阶次p的确定.
图4即为所绘制出的图1所示信号的AIC(p)曲线.由图4的AIC(p)曲线,可确定对于汽轮机振动信号分析最佳模型阶次应该为p=43.
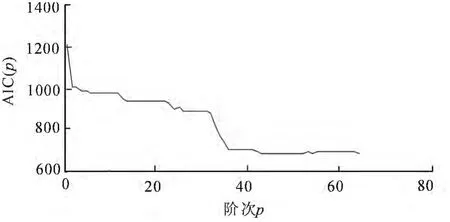
图4 AIC(p)曲线图形Fig.4 Curve of AIC(p)
2.5 进一步改进方差性能的措施
在振动信号的噪声较大时,方差性能对谱估计的效果有比较重要的影响.在将最小方差谱估计算法与AIC准则相结合的基础上,再对其进行加窗处理,能更进一步提高其方差性能.在谱估计中经常采用的窗函数有矩形窗、汉明窗等。这些窗函数对方差性能的提高效果不显著,且会明显影响分辨力性能.论文将最优窗函数法[15]引入到汽轮机振动信号的最小方差谱估计中。最优窗函数法是基于最优化的一种方法,通过使平均频率误差最小,使其谱估计性能进一步优于汉明窗等函数法.m阶最优窗公式为
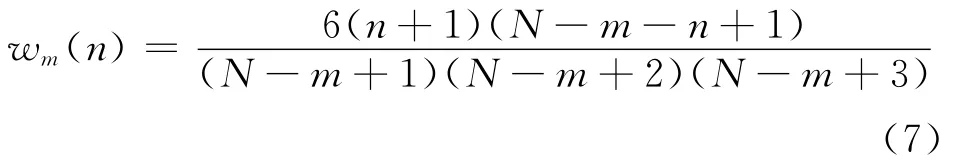
式中:N为信号长度,n为可知最优窗只与信号长度与阶次有关,与信号的幅值、频率无关,所以将该窗与最小方差谱估计算法相结合,可以有效抑制谱估计中的诸如谱分裂等现象,进一步提高方差性能.
3 汽轮机振动信号谱分析的效果
取最佳阶次p=43,通过Matlab仿真程序可得AR模型算法功率谱图,如图5所示.
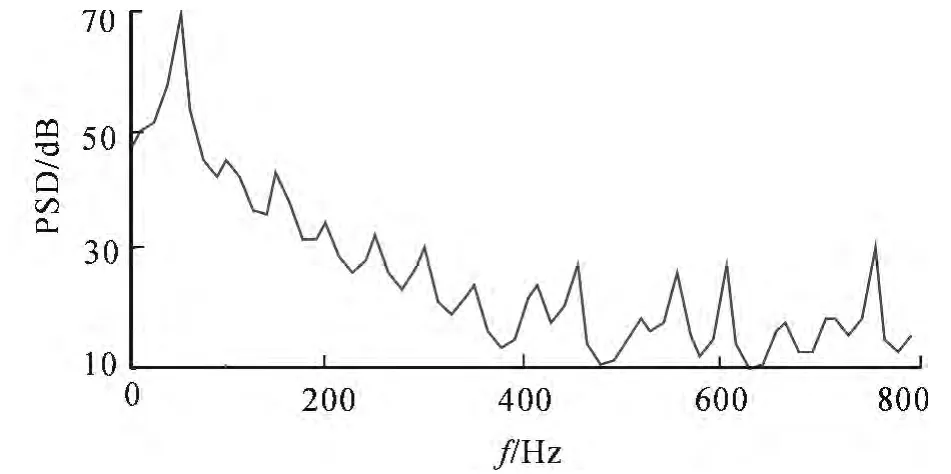
图5 AR模型算法谱图(p=43)Fig.5 Spectrum based on AR Method
对比图6和图2,最小方差谱估计算法与周期图法具有基本相当的频率分辨力,但方差性能远远优于传统的周期图法.

图6 最小方差谱估计算法谱图(p=43)Fig.6 Spectrum based on MVSE Method
对比图6和图3,最小方差谱估计算法的方差性能与 Welch算法相当,但分辨力要优于 Welch算法.
对比图6与图5,最小方差谱图对汽轮机振动信号中的各次谐波成分均能较好的分辨,且方差性能比AR模型要好,谱分析具有较好的准确性.
对比分析可表明,最小方差谱估计算法只要模型阶次选取合适并结合进行加窗处理,能够在保证谱分析的分辨力性能的基础上提高方差性能,谱估计效果优于经典算法.具体在汽轮机振动信号分析中,在采样数据较短的情况下,最小方差谱估计算法能够较为准确的进行谐波分析,克服了经典算法应用的局限,同时方差性能优于AR模型算法,适合于振动信号的谱分析.
4 结 论
1)最小方差谱估计算法应用于汽轮机振动信号分析可克服经典算法在实际应用中无法进行短数据谱分析的局限,能够获得较好的谐波分析效果.
2)最小方差谱估计算法是在AR模型算法基础上的改进,方差性能要优于AR模型.
3)将AIC准则及最优窗引入到汽轮机最小方差谱估计算法中,在基本保证分辨力性能的情况下,方差性能得到进一步改善,对汽轮机振动信号谱估计的抗噪声性能有很好的效果.
[1] 许萍萍,韩雪山,何渊井.运输过程振动信号功率谱估计的实现[J].物流技术,2013,32(4):189.XU Ping-ping,HAN Xue-shan,HE Yuan-jing.Realization of PSD Estimation of Vibration Signals in Transportation Process[J].Logistics Technology,2013,32(4):189.(in Chinese)
[2] 张峰,石现峰.汽轮机振动信号频谱分析方法的仿真研究[J].计算机技术与发展,2010,6(2):126.ZHANG Feng,SHI Xian-feng.Study and Simulation of Spectrum Analytical Methods for Turbin’s Vibration Signal[J].Computer Technology and Development,2010,6(2):126.(in Chinese)
[3] 邓泽怀,刘波波,李彦良.常见的功率谱估计方法及其Matlab仿真[J].电子科技,2014,27(2):50.DENG Ze-huai,LIU Bo-bo,LI Yan-Liang.Common Power Spectrum Estimation Methods and Matlab Simulation[J].Electronic Technology,2014,27(2):50.(in Chinese)
[4] 石国德,王明皓,吕朝晖.空间谱估计经典算法性能比较[J].电子设计工程,2013,23(2):190.SHI Guo-de,WANG Ming-hao,LYU Chao-hui.Performance Comparison Between Classic Algorithms for Spatial Spectrum Estimation[J].Electronic Design Engineering,2013,23(2):190.(in Chinese)
[5] 杨皓,黄东胜.AR模型应用于振动信号趋势预测的研究[J].南京工程学院学报:自然科学版,2007,5(2):45.YANG Hao,HUANG Dong-sheng.A Study of AR Model Based on Burg Arithmetic for Trend Forecast of Vibration Signals[J].Journal of Nanjing Institute of Technology:Natural Science Edition,2007,5(2):45.(in Chinese)
[6] 胡光书.数字信号处理——理论、算法与实现[M].北京:清华大学出版社,2004.HU Guang-shu.Digital Signal Processing:Principles,Algorithms and Application[M].Beijing:Tsinghua University Press,2004.(in Chinese)
[7] AKAIKE H.A New Look at the Statistical Model I-dentification[J].IEEE Transactions on Automatic Control,1974,13(6):128.
[8] SMITH D E.IPTV Bandwidth Demand:Multicast and Channel Surfing[C]//Proceedings of IEEE Conference on Computer Communications (INFOCOM 2007).Anchorage,AK:[s.n.],2007:2546.
[9] YU G,WESTHOLM T,KIHI M,et al.Analysis and Characterization of IPTV User Behavior[C]//Proceedings of IEEE International Symposium on Broadband Multimedia Systems and Broadcasting,2009.Bilbao,SPAIN:IEEE Broadcast Technology Society,2009:650.
[10] SCHMIDT R O.Multiple Emitter Location and Signal Parameter Estimation[J].IEEE Transactions on Antennas Propag,1986,34(3):276.
[11] 张峰,张馨月,马舒啸,等.汽轮机振动信号的自回归模型谱估计算法[J],西安工业大学学报,2013,33(12):1004.ZHANG Feng,ZHANG Xin-yue,MA Shu-xiao,et al.Auto Regression Model’s Spectrum Estimation Algorithm for Turbine’s Vibration Signal[J].Journal of Xi’an Technological University,2013,33(12):1004.(in Chinese)
[12] 张峰,石现峰,张学智.Welch功率谱估计算法研究及仿真分析[J].西安工业大学学报,2009,29(4):353.ZHANG Feng,SHI Xian-feng,ZHANG Xue-zhi.Study and Simulation of Welch Power Spectrum Estimation Method[J].Journal of Xi’an Technological University,2009,29(4):353.(in Chinese)
[13] 李明,王晓茹.基于最优窗burg算法的电力系统间谐波谱分析[J].电工技术学报,2011,26(1):178.LI Ming,WANG Xiao-ru.Inter-Harmonic Spectral Estimation in Power System Based on the Optimal Window Burg Algorithm[J].Transactions of China Electrotechnical Society,2011,26(1):178.(in Chinese)
[14] WAX K.Detection of Signals by Information Theoretic Criteria[J].IEEE Transactions on ASSP,1985,33(2):387.
[15] 余训锋,马大玮,魏琳.改进周期图法功率谱估计中的窗函数仿真分析[J].计算机仿真,2008,25(3):111.YU Xun-feng,MA Da-wei,WEI Lin.Simulation A-nalysis of Window Function in Power Spectrum Estimation Based on Modified Periodogram[J].Computer Simulation,2008,25(3):111.(in Chinese)
