随机森林的变量捕获方法在高维数据变量筛选中的应用*

宋欠欠李轶群侯 艳李 康△

随机森林的变量捕获方法在高维数据变量筛选中的应用*

宋欠欠1李轶群2侯 艳1李 康1△

目的探讨随机森林（RF）的变量捕获方法在高维数据变量筛选中的应用。方法通过模拟实验和实际数据分析，对两种变量捕获（vh.md，vh.vimp）和逐步剔除方法（varSelRF）进行比较，并通过选入变量的数目、模型预测错误率（PE）和受试者工作特征曲线下面积（AUC）对其进行评价。结果模拟实验表明，在变量具有联合作用、交互作用和弱独立作用情况下，变量捕获方法均明显优于varSelRF方法和全变量VIMP排序方法；实际数据分析结果表明，变量捕获方法筛选变量结果稳定，并能够保证良好的预测效果。结论变量捕获方法适用于高维数据的变量筛选，具有实用价值。

随机森林 变量筛选 变量捕获

高通量组学技术的迅速发展促进了研究者们从分子水平上研究疾病的发生和发展过程，成为生物学研究的有力工具。另一方面，高维组学数据的特点使得传统的方法不再可行，对统计学和生物信息学数据分析提出了重大挑战。近年来，随机森林（random forest，RF）方法在高维组学中得到广泛应用，它是一个非参数的基于树的组合分类器（模型），能够有效地处理高维变量问题［1］。RF的重要特点是可以对变量的重要性进行排序，识别与疾病有关的基因、蛋白、代谢物等生物标志物，同时能够对数据进行分类。然而，通常情况下组学数据变量数目巨大（如m＞2000），且对预测有作用的变量数目p占总变量数目m的比例很小（如p／m＜0.05），建立的RF模型容易受到对分类不起作用变量的干扰，使变量重要性排序和分类效果下降，甚至完全失效［2-6］。为此，Ishwaran等人给出了变量捕获（variable hunting）方法［7-9］，用来解决这一问题。本文在简要介绍这一方法的基础上，通过模拟实验和实际数据探索其适用性，并与直接使用RF方法及目前使用较多的变量逐步剔除方法（backwards variable elimination using random forests，varSelRF）进行比较［10］。

原理与方法

1.随机森林的基本思想

RF的基本思想是通过自助法（bootstrap）重抽样技术从原始数据中有放回的随机抽取Ntree个自助样本，作为训练样本，对每个样本都建立一个二元递归分类树。每个自助样本平均不包含37%的原始数据，将这些数据称为袋外数据（out of bag data sets，OOB）并作为RF的测试样本；最后，由训练样本生成Ntree个分类树组成随机森林，根据分类树的投票确定测试样本的分类结果［1-2］。变量的筛选可以依据不同的统计量和筛选过程。

2.衡量变量重要性的统计量

（1）VIMP统计量 计算置换变量的重要性（permutation variable important，VIMP）。具体地，测量一个变量Xi（i∈1，2，…，m）的重要性，首先建立样本数据的随机森林（RF），然后对所有OOB样本中这个变量的值进行随机打乱，并根据建立好的RF模型对每一个体所属类别进行预测，计算该变量扰乱前后OOB的预测错误率的改变大小。对于所有的树，变量扰乱前后OOB预测错误率改变的平均值作为置换变量的重要性评分［1，4］。

（2）最小深度统计量 从树的根结点到最近的变量Xi的最大子树的根结点的距离称为变量Xi的最小深度。变量Xi的最大子树越接近根节点，其预测作用越大。最小深度的分布和变量筛选的阈值都可以计算出来［8-9］。在高维数据中，假设变量与分类变量无关，D（ζ）是树ζ的深度，其概率分布为

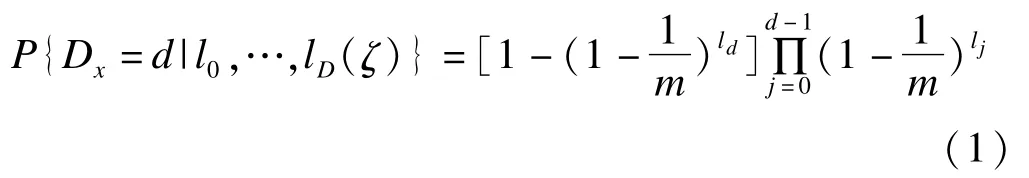
其中ld等于深度为d时非终节点的数目，m为变量的数目。

3.变量捕获方法

这是一种再抽样和向前选择变量的方法，由Ishwaran等人提出［8-9］。首先，从数据中随机抽取一个子集（如五折抽样，其中四份为训练样本，其余一份为预测样本），同时随机选择一部分变量（如m／5）；应用选择的数据和变量构建RF，变量排序可以使用VIMP统计量（variable hunting with variable importance，vh.vimp）或最小深度统计量（variable hunting with minimal depth，vh.md）。选择最小深度阈值作为最初的模型，然后根据最小深度或VIMP的排序将变量逐步增加到最初的模型中，直到模型的联合VIMP统计量稳定为止，并作为最终模型。联合VIMP统计量的计算原理同前，但需要同时置换多个变量。上述过程重复nrep次，计算平均筛选变量的个数（取近似整数值p），再根据各变量被筛选出来的频率进行排序，选择排列在前面的p个变量作为最终筛选出的重要变量。最后，应用筛选出的变量对样本数据给出一个新的RF模型。

上述过程可以使用R语言程序包randomForestSRC实现。

模拟实验

实验目的：构建具有不同作用的变量，并加入一定数目的噪声变量，考察基于VIMP的变量捕获方法（vh.vimp）和基于最小深度的变量捕获方法（vh.md）的筛选效果，同时与目前使用较多的变量逐步剔除方法（varSelRF）和直接使用VIMP统计量排序方法进行比较。

1.模拟实验一

实验设置：设置3个具有联合分类作用的变量X1，X2，X3，且均为二分类编码（1表示高表达，0表示低表达），3个变量有8种不同的组合方式，不同组合出现的概率不同，并与取值是否为“1”或“0”有极强的关系，如图1所示。按照这种方式随机产生2组上述联合分类变量，即X1，X2，…，X6，其中X4，X5，X6，产生方式同X1，X2，X3，且各变量对于分类贡献等同。随机产生2000个标准正态分布噪声变量Z～N（0，1），疾病组（D＝1）与对照组（D＝0）的样本含量设置为n1＝n2＝50，形成模拟数据。同时产生两组样本量均为200的测试数据集。

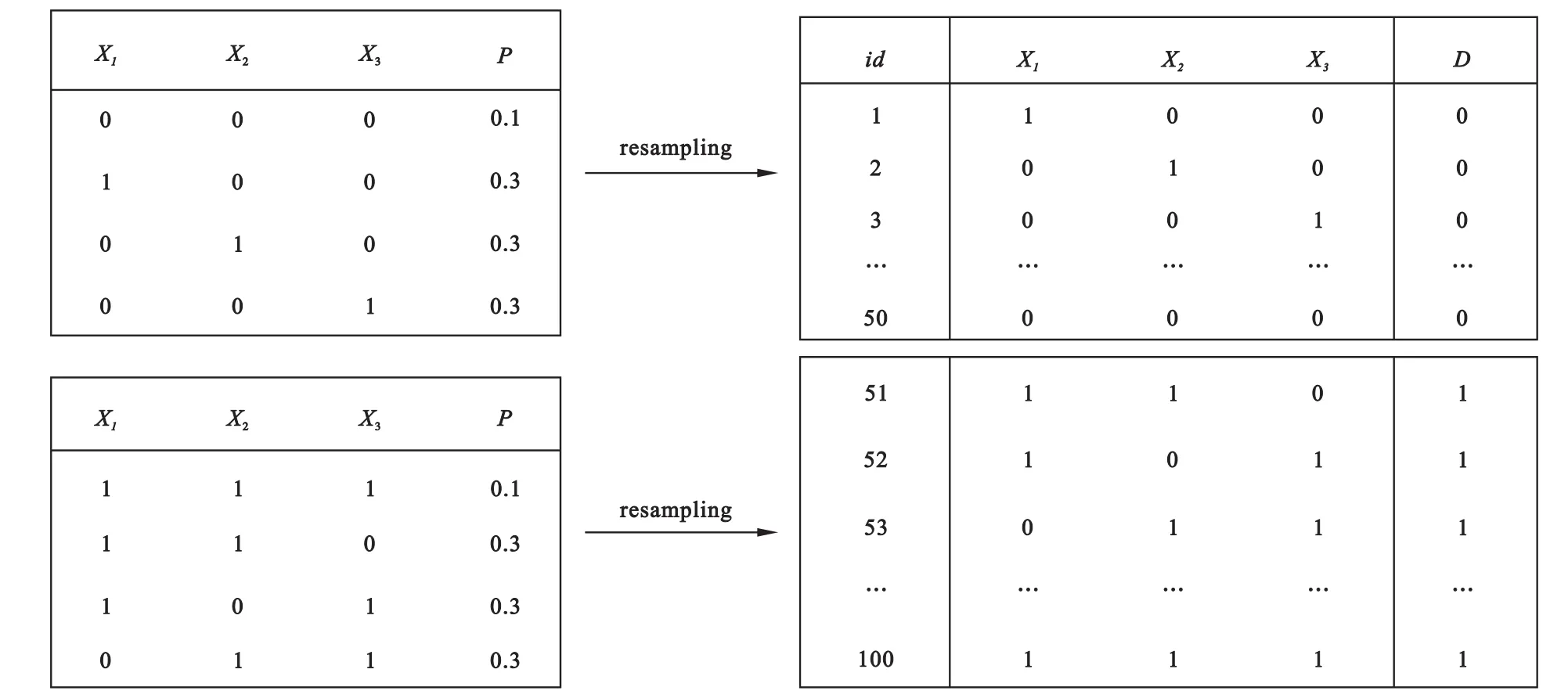
图1 二分类联合作用变量的模拟数据产生示意图

模拟方法：应用vh.vimp、vh.md和varSelRF程序对训练数据进行变量筛选，并使用所有变量应用VIMP对其进行排序，记录前10（vimp10）、25（vimp25）和50（vimp50）个变量中含有设定的差异变量的情况。根据筛选出的变量计算变量筛选的假发现率（false discovery rate，FDR），同时应用筛选后的训练数据建立RF模型，并对预测数据进行预测，应用预测误分错误率（predicted error rate，PE）和ROC曲线下面积（area under the receiver operating characteristic curve，AUC）进行评价。模拟重复100次，结果见表1。

模拟结果：表1给出了varSelRF、vh.vimp和vh.md在模拟实验中筛选的变量个数、包含差异变量的个数、假发现率和变量筛选前后随机森林预测效果的评价统计量的平均值，同时给出了根据随机森林全部变量VIMP的大小进行排序后选择前10、25、50个变量时包含真实差异变量的情况。结果表明，在二分类联合作用条件下，varSelRF、vh.vimp和vh.md均能筛选出较多的差异变量，而基于全部变量的VIMP排序则不能够达到较好的变量筛选效果。同时注意到，varSelRF筛选的变量结果极不稳定（四分位数间距为34），而vh.md方法虽然能够筛选出所有的差异变量，但却具有较高的FDR值。总之，三种方法中vh.vimp方法筛选变量的FDR值最小，结果稳定，其预测效果最好。

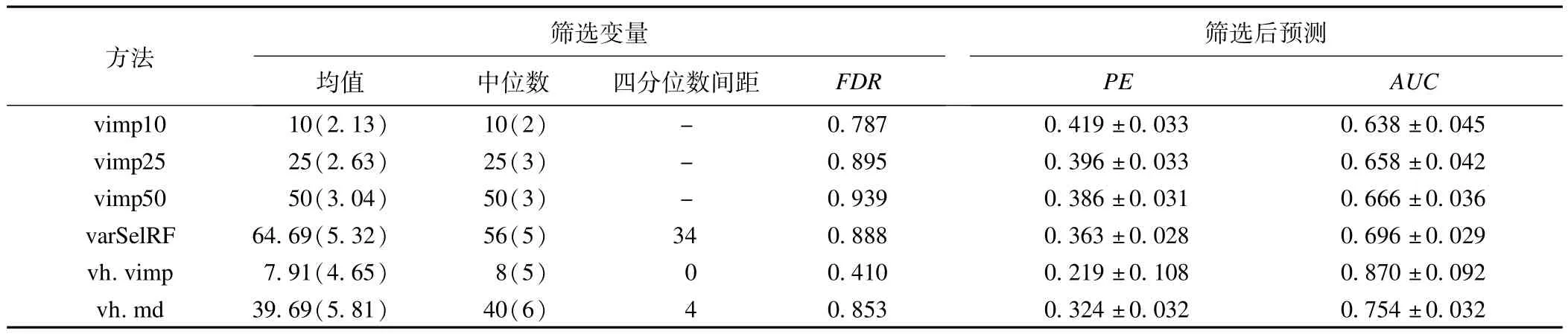
表1 具有变量联合作用时几种变量筛选方法的模拟实验结果

2.模拟实验二

实验设置：设置具有交互作用的变量。两个差异变量Z1和Z2服从正态分布，疾病组服从Z1～N（1，1）和Z2～N（5，1），对照组服从Z1～N（0，1）和Z2～N（0，1），两变量的相关系数为0.6。做变量变换X1＝Z1，X2＝Z2／Z1，即X1和X2具有一阶交互作用。应用同样方式，给出｛X3，X4｝，｛X5，X6｝，｛X7，X8｝，｛X9，X10｝，每个单变量AUC≈0.76。另外，随机产生2000个服从标准正态分布的变量作为噪声变量（n1＝n2＝50），形成模拟数据，用于变量筛选和建立RF模型，同时产生两组样本量均为200的测试数据集用于变量筛选后RF模型的预测。模拟重复100次。

表2给出了varSelRF、vh.vimp、vh.md和基于全部变量显示VIMP排序方法在存在交互作用时模拟实验情况。结果显示，变量捕获方法明显优于varSelRF方法，虽然varSelRF方法也能较好地筛选出差异变量，但其稳定性上明显不如前者，同时变量捕获方法有更低的FDR值。由于设定的差异变量作用很强，在包含所有变量的VIMP方法中这些变量也排在了最前面。

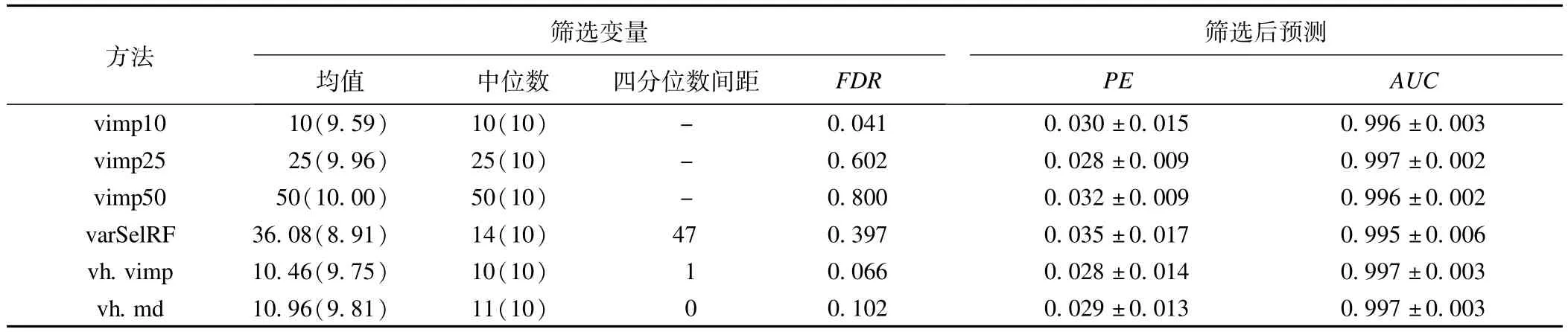
表2 具有变量交互作用时几种变量筛选方法的模拟实验结果

3.模拟实验三

实验设置：设置具有作用较弱且相互独立的差异变量。病例组每个差异变量服从X～N（0.5，1）的正态分布，对照组服从标准正态分布X～N（0，1），每个单变量AUC≈0.62，共10个差异变量。在两组中，随机产生4000个正态分布噪声变量X～N（0，1）。样本量设置为n1＝n2＝50，形成模拟数据，进行变量筛选并用筛选后数据建立RF模型，同时应用上述模拟产生200例测试数据用于评价RF模型，模拟重复100次。

模拟结果：表3给出了varSelRF、vh.md、vh.vimp和基于全部变量的VIMP排序方法在模拟实验中进行变量筛选的情况。结果显示，varSelRF、vh.md和vh.vimp在一定程度上能够达到变量筛选的效果，但漏选的变量较多。相比而言，两种基于变量捕获方法筛选的变量个数均比较稳定，并具有较低的FDR值（FDR＜0.45），而varSelRF筛选的变量个数较多且不稳定，并有较高的FDR值。

实例验证

选用课题组研究的四个代谢组数据进行分析，数据的基本情况如表4。利用7折交叉验证方法，将实际数据划分为训练数据和测试数据，使用随机森林的两种变量捕获方法（vh.md，vh.vimp）和逐步剔除（varSelRF）方法，对训练数据进行变量筛选，然后应用筛选后的训练数据建立RF模型，对测试数据进行预测和评价。随机重复10次7折交叉验证，计算平均值。

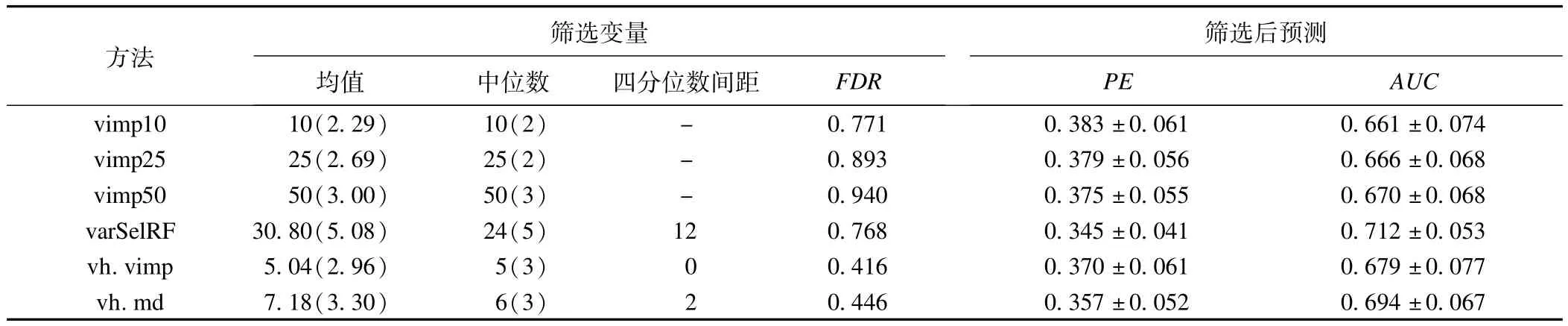
表3 具有变量弱独立作用时几种变量筛选方法的模拟实验结果

表4 实际代谢组数据的样本分布情况

表5给出了四个代谢组数据使用三种不同方法筛选的变量个数和预测情况。

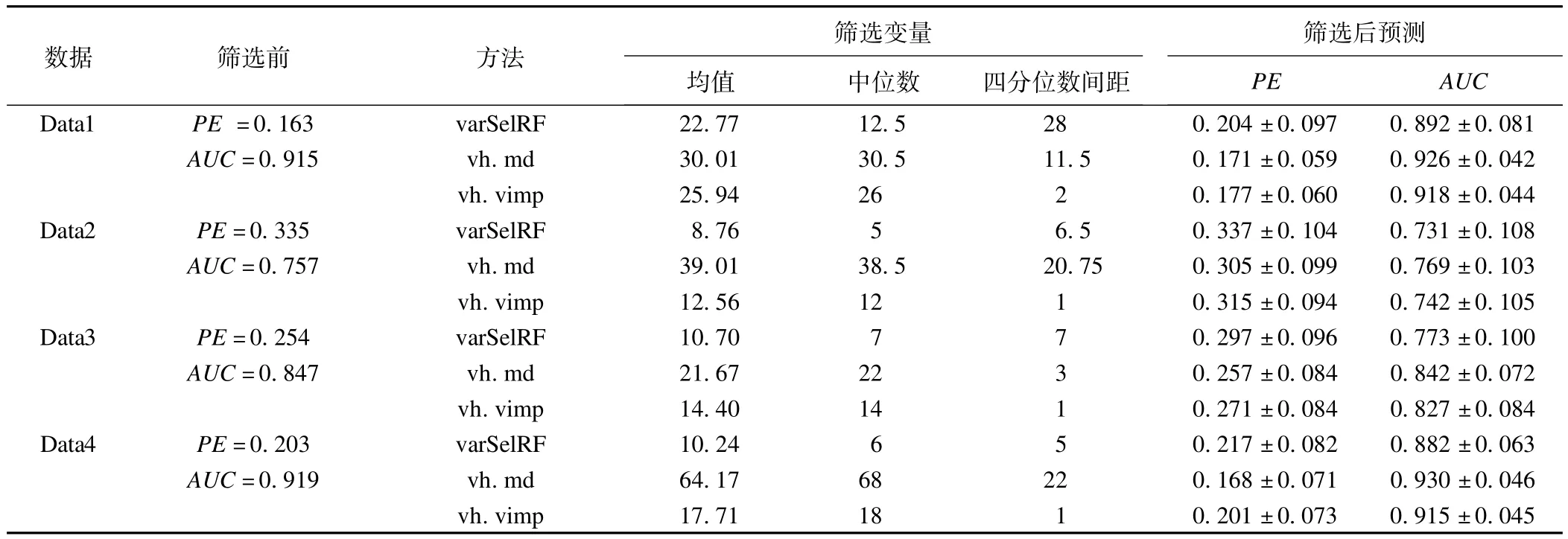
表5 随机森林（RF）筛选变量的三种方法分析结果

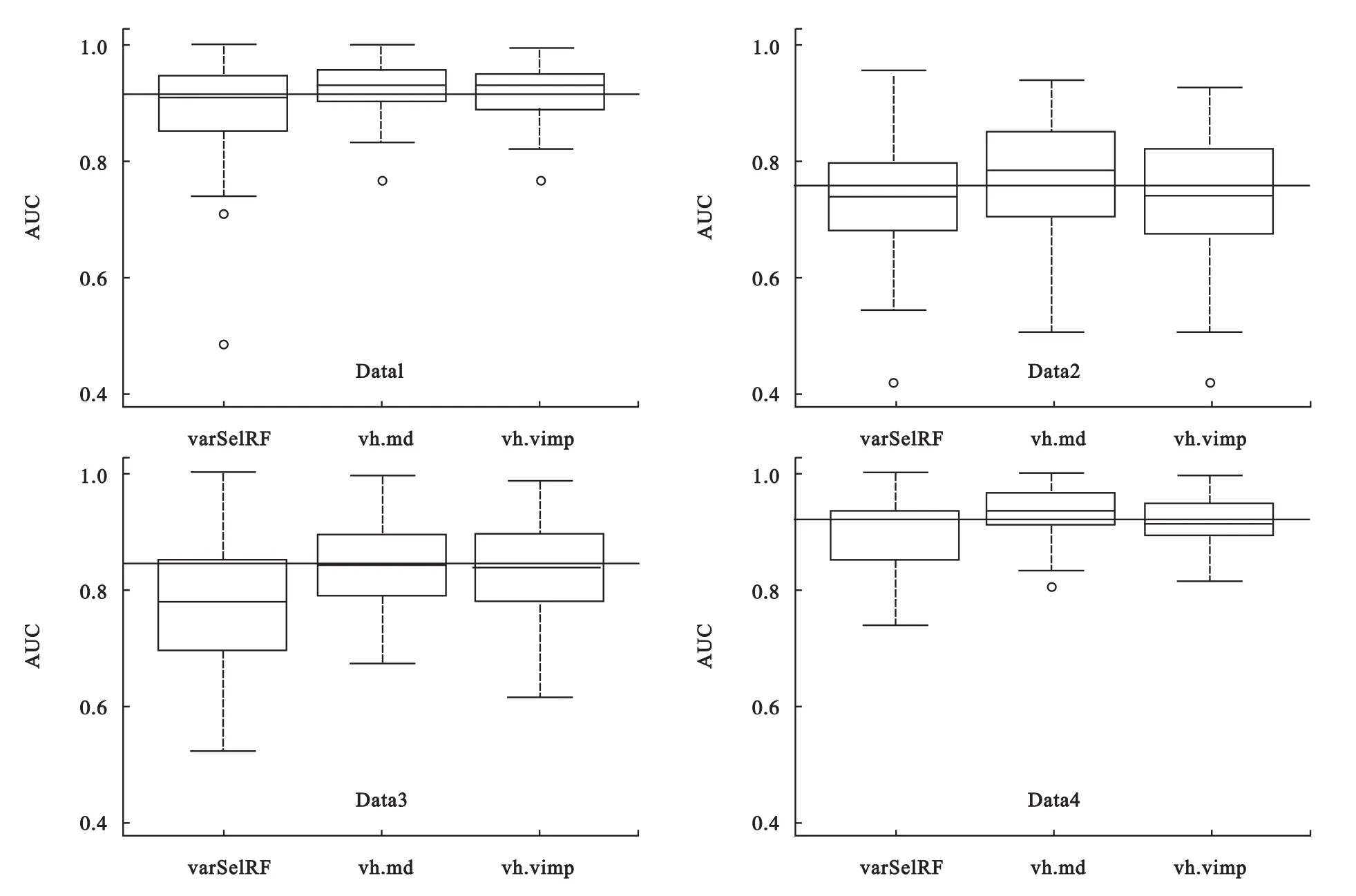
图2 实际四组代谢组数据中应用三种筛选变量方法建立的RF预测结果

结果显示，三种方法筛选变量后建模，其预测能力与使用全部变量相近，vh.md和vh.vimp方法优于varSelRF（图2）。从变量筛选上看，varSelRF筛选的变量总数较少，vh.vimp在三种方法中筛选的变量个数适中，其四分位数间距最小，筛选变量的结果最为稳定和可靠。

讨 论

1.RF是一个组合决策树方法，具有抗噪声、防止过拟合、不受共线影响和能够处理非线性数据等优点，可用于高维组学数据的变量筛选和预测。在变量很多的情况下，RF变量筛选容易受大量无作用的噪声变量的干扰，直接使用VIMP进行排序可能不准确，而且各变量之间的VIMP相互影响，无法用标准化的方法给出筛选变量的阈值。

2.varSelRF方法是一种向后选择变量的方法，其基本思想是不断去除VIMP排在后面的变量，减少噪声变量的干扰，使前面的变量排序更加准确，再不断去除可能没有作用的变量，选择OOB错误率最小的变量集。这种方法的主要问题是，如果有比较多的差异变量，而且一些变量之间具有较强的相关性（信息重叠），遵照“最节省原则”，可能会使很多变量不能被选入RF模型。另外，如果数据中含有作用很大的变量，其他作用相对较弱的变量就不容易选入模型，从实例验证可以清楚地看到这一点。模拟实验中没有显示相应的结果，原因是设置的差异变量的作用相同。varSelRF方法的最大问题是筛选变量的结果不稳定。

3.相对而言，变量捕获方法是一种更好的变量筛选方法。其基本思想是利用重抽样方法不断抽取一定比例的样本，同时在所有变量中抽取一定数量的变量进行建模，核心是利用最小深度统计量的概率分布确定阈值，在此基础上向前进行变量筛选。理论上，这种方法可以应用于任意高维变量的组学数据中，拓宽了RF的应用范围。本文在模拟实验中，应用FDR值进行变量筛选效果的评价，同时对基于筛选变量后的训练数据建立RF模型，并使用预测错误率以及AUC值两个指标进行预测效果评价。模拟实验证实，即使在变量作用较弱的情况下，仍能够保证筛选的变量具有较低的FDR值，特别是vh.vimp方法在本文中给出的各种情况下，筛选变量的稳定性非常好，而且其筛选后变量的预测效果略优，结果更为可信。在实际数据分析中，本文应用筛选变量后的训练数据建立RF模型并应用测试数据对筛选效果进行评价，结果表明vh.vimp和vh.md均在一定程度上优于varSelRF方法。

4.变量捕获方法本质上是一种筛选变量的策略，筛选时可以使用不同的统计量。事实上，改变筛选变量过程的不同参数，可以获得不同数量的“差异变量”，如本文确定RF模型变量的数目是根据再抽样样本选入变量的平均值，实际中也可以设定其他参数（如P75）进行变量筛选。

1.Breiman L.Random forests.Machine Learning，2001，45（1）：5-32.

2.武晓岩，李康.随机森林方法在基因表达数据分析中的应用及研究进展.中国卫生统计，2009，26（4）：437-440.

3.Wu X，Wu Z，Li K.Classification and identification of differential gene expression for microarray data：improvement of the random forest method.International Conference on Bioinformatics and Biomedical Engineering，2008.

4.Wu X，Wu Z，Li K.Identification of differential gene expression form icroarray data using recursive random forest.Chinese Medical Journal，2008，121（24）：2492-2496.

5.Strobl C，Boulesteix AL，Zeileis A，et al.Bias in random forest variable importance measures：illustrations，sources and a solution，BMC Bioinformatics，2007，8（25）.

6.Biau G，Devroye L，Lugosi G.Consistency of random forests and other averaging classifiers，Journal of Machine Learning Research，2008，9：2015-2033.

7.Ishwaran H，Kogalur UB，Blackstone EH，et al.Random survival forests.The Annals of Applied Statistics，2008，2（3）：841-860.

8.Ishwaran H，Kogalur UB，Gorodeski EZ，etal.High-Dimensional Variable Selection for Survival Data.Journal of the American Statistical Association，2010，105（489）：205-217.

9.Ishwaran H，Kogalur UB，Chen X，et al.Random survival forests for high-dimensional data.Statistical Analysis and Data Mining，2011，4（1）：115-132.

10.Díaz-Uriarte R，Alvarez de Andrés S.Gene selection and classification of microarray data using random forest.BMC Bioinformatics，2006，7（3）.

（责任编辑：刘 壮）

The Application of a Random Forest-based Variable Hunting Method to Variable Selection in High-dimensional Data

Song Qianqian，Li Yiqun，Hou Yan，et al（Department of Medical Statistics，Harbin Medical University（150081），Harbin）

ObjectiveThis project explored the application of a random forest-based variable hunting approach to variable selection in high-dimensional data.MethodsTwo variable hunting methods（vh.md，vh.vimp）were compared with backwards variable elimination using random forest（varSelRF）by the analysis of simulation data and real metabonomics data，and then variable numbers，predicted error rate（PE）and the area under the receiver operating characteristic curve（AUC）were used to evaluate these approaches.ResultsSimulation experiments suggested that variable hunting method was more effective than varSelRF and sorted VIMP method，in the case of combined effects，interactions and weak independent effects.Analysis results of metabonomics data confirmed that the results of variable selection were stable and had favorable predictive effects with the variable hunting method.ConclusionThe variable hunting approach was applicable to variable selection in high-dimensional data and possessed practical value.

Random forest；Variable selection；Variable hunting

*：国家自然科学基金资助（81172767）；高等学校博士学科专项基金（20122307110004）

1.哈尔滨医科大学卫生统计学教研室（150081）

2.哈尔滨医科大学生物信息教研室

△通信作者：李康，E-mail：likang＠ems.hrbmu.edu.cn