核正交偏最小二乘在代谢组学数据分析中的应用*

哈尔滨医科大学卫生统计学教研室（150081） 李俊南 侯 艳 李 康

核正交偏最小二乘在代谢组学数据分析中的应用*

哈尔滨医科大学卫生统计学教研室（150081） 李俊南 侯 艳 李 康Δ

目的探索核正交偏最小二乘方法的特点及其在代谢组学数据分析中的应用。方法通过模拟实验和真实代谢组学数据，评价核正交偏最小二乘方法的模型预测能力及其可视化效果。结果模拟数据分析表明，当数据间存在线性关系时，KOPLS与传统的线性OPLS具有相同的效果；当数据间存在非线性关系时，KOPLS具有相对更高的预测能力，得分图的可视化效果更好。实际数据分析结果显示，应用KOPLS能够提高模型预测能力和改善可视化效果。结论对于高维非线性关系的代谢组学数据更适合使用KOPLS方法。

核正交偏最小二乘 非线性 代谢组学

偏最小二乘（partial least squares，PLS）是当前在计量化学和代谢组学领域中有监督分析的常用方法。偏最小二乘利用潜变量的概念，描述自变量矩阵X和因变量矩阵Y之间的关系，可以用于处理高维数据［1］。正交偏最小二乘（orthogonal projections to latent structures，OPLS）是继PLS回归之后发展的一种处理高维数据的方法。该方法利用正交信号校正（orthogonal signal correction，OSC）的思想，把与Y无关的正交变量从预测结果中分离出来。从预测的角度看，当只有一个因变量时，PLS和OPLS方法的预测效果相等，由于预测得分和载荷矩阵与正交变量没有关系，所以OPLS方法增强了模型的解释性［2］。

在计量化学和生物学系统中，X和Y之间有可能是非线性的关系，此时利用OPLS或者PLS分析数据，会使结果变差。Rosipal和Trejo首次将核函数引入到偏最小二乘回归中，用来处理非线性问题［3］。Mattias等人2008年提出了核正交偏最小二乘方法［4］，这种方法继承了OPLS方法的基本思想，进一步在特征空间内分离预测成分和正交成分，提高预测能力和分类可视化效果［5］。本文在简单介绍KOPLS方法和原理的基础上，通过模拟试验和实际数据，说明KOPLS方法在高维数据及代谢组数据分析中的适用性。

原理与方法

1.基本原理

核正交偏最小二乘（KOPLS）将原始的X空间的数据映射到一个高维特征空间F｛x∈X→Φ（x）∈F｝，并在特征空间里使用线性OPLS方法解决原始空间的非线性关系。核点积定义为k（x，y）＝〈φ（x），φ（y）〉，需要计算全部的Ki，j＝k（xi，xj）（其中xi，xj分别代表自变量矩阵的第i行和第j行），通过使用合适的核函数，可以避免确定X映射到特征空间的映射函数，同时不用在特征空间内计算“点积”，其计算非常方便。KOPLS的建模过程见图1。常见的核函数有线性核函数（式1）、多项式核函数（式2）和径向基核函数（通常被称为高斯核函数）（式3）。

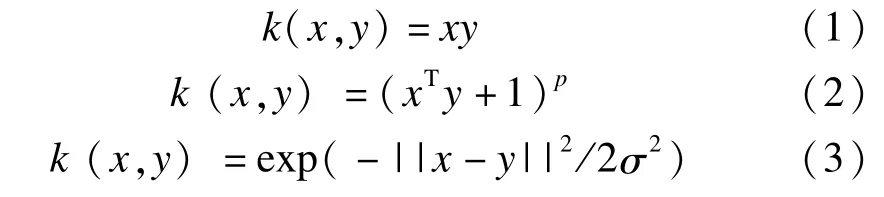
实际中最常用的方法是高斯核函数［5］。例如，给定xi和xj

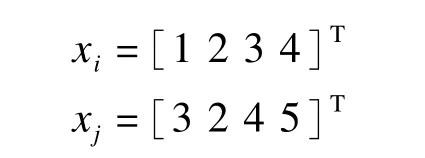
那么核矩阵K的元素ki，j可以计算为

应用高斯核函数的重点是参数σ的选择，其影响模型的预测能力。在实际中，我们根据研究目的选择核参数。

KOPLS模型包括一系列的预测成分Tp和一系列的正交成分To，去除正交成分后，把变异都集中在一个预测成分中，模型解释简单。KOPLS方法把Y预测成分和Y正交成分进行分离并没有影响预测能力，这种方法还可以识别数据中的异常现象，如仪器零点漂移、批次的不同或者其他的生物变异等，而通过其他方法可能难以识别这些现象。例如，如果两类数据可以通过KOPLS得分图的正交成分分开，则说明其与有意义的差异变量无关，可能是由于批次不同等非差异变量引起的。

图1 KOPLS的建模过程示意图

2.计算方法

（1）核矩阵中心化

对于数量级差别较大的数据，在建模之前需要对数据进行标准化和对核矩阵K进行中心化，式（4）描述了核矩阵的中心化过程。

其中，In是n维单位矩阵，En代表一个（n×1）的向量，它的元素等于1。

（2）建立KOPLS模型

K表示核矩阵，Ao表示正交成分个数，Ki表示被第i个正交成分抽取之后的核矩阵，Qi表示Ki被A个预测成分抽取之后的核矩阵。具体步骤如下：

①通过特征向量YTKY分解估计预测Y权重向量Cp；

②把Y映射到CP上，得到Y预测得分矩阵Up∶Up⇐YCp；

③计算X预测得分矩阵Tp∶Tp⇐KUp；

④循环迭代i从1到Ao；

计算Y正交得分向量toi∶toi⇐QiTpCo；

通过to，t抽取Ki，形成Ki＋1；

更新预测得分矩阵：Tp⇐Ki＋1Up；

循环结束；

模拟试验

实验目的：通过模拟线性和非线性相关关系的数据，探索KOPLS方法的特点及适用条件，并与常用的OPLS方法进行比较。模型的预测能力通过7折交叉验证得到的Q2统计量衡量，Q2越大说明数据中含有生物标志物的可能性越大，其诊断效果越好，同时存在过拟合的风险较小，可视化效果通过绘制主成分得分图进行判断。KOPLS方法通过R语言编程实现。

模拟实验1：设有两组数据，其中有20个差异变量，在两个不同的分组中分别服从X1～N（0，1）和X2～N（1.0，1）的正态分布，产生线性相关关系的数据，同时加入500个无差异变量作为干扰变量，干扰变量在两类中均服从X～N（0，1）的正态分布，并分为25组，每组20个变量的相关系数均等于0.8，分别利用KOPLS和OPLS进行分析，首先对数据进行标准化，KOPLS使用高斯函数，得出每种方法的Q2值，以及绘制得分图来观察两种方法的可视化效果，上述实验重复1000次，得出平均Q2值，见图2。

图2 KOPLS（a）和OPLS（b）方法的Q2值

从图2中可以看到KOPLS去除4个正交成分时，Q2最大，Q2＝0.905，OPLS去除4个正交成分时，Q2最大，Q2＝0.892，通过绘制两种方法的得分图（图3），我们可以看到两种方法都能将两类明显的区分开。说明当数据间存在线性相关关系时，KOPLS方法与OPLS方法的结果基本相同。

模拟试验2：产生非线性相关关系的数据，为此先产生正态分布数据，然后通过x＝5（exp（-X）-4exp（-2X）＋3exp（-3X））变换得到模拟数据。模拟设定在第一类中有20个差异变量，均独立服从XK～N（1.8，1），在第二类中20个变量均服从XK～N（0，1）的正态分布，加入与模拟试验1设置相同的干扰变量。对上述模拟数据分别利用KOPLS方法和OPLS方法进行分析，分别计算每种方法的Q2值，以及绘制得分图来观察两种方法的分类能力和可视化效果，上述方法重复实验1000次，得出平均Q2值，KOPLS方法使用高斯核函数，核参数σ＝20，两种方法的Q2结果见图4。

从图中可以看到，KOPLS去除1个正交成分时最大，Q2＝0.612，当进行OPLS分析时，其Q2为负值，去除一个正交成分后，通过绘制两种方法的得分图（见图5），我们可以看到KOPLS很明显的将两类区分开，而OPLS方法却区分的不够好，说明KOPLS在因变量与自变量成复杂的非线性关系时，具有较好的模型拟合和预测效果，而且可视化效果更佳。

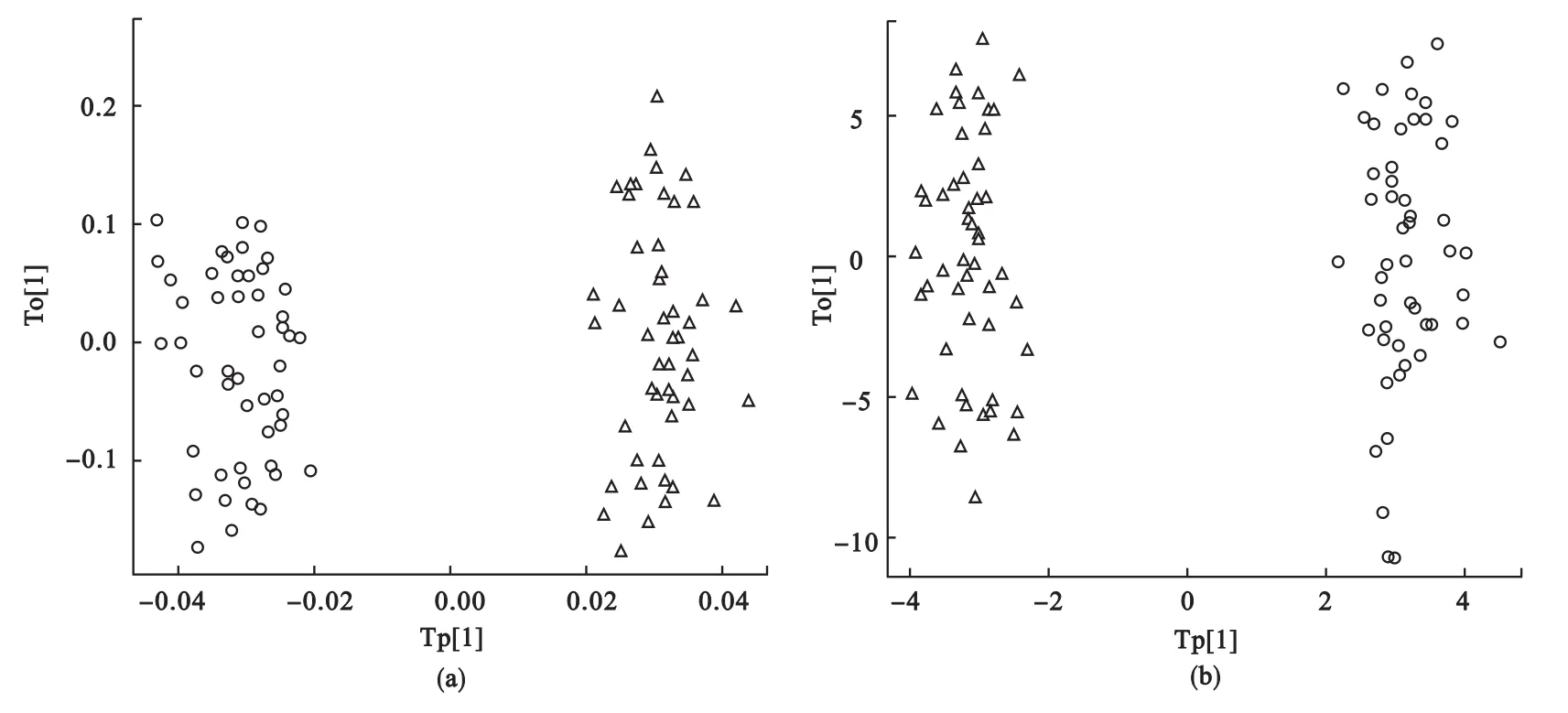
图3 KOPLS（a）和OPLS（b）的预测成分和第一个正交成分的得分图

图4 KOPLS（a）和OPLS（b）方法的Q2值

图5 KOPLS（a）和OPLS（b）的预测成分和第一个正交成分的得分图

实例分析

选取课题组研究的卵巢癌代谢组数据，共包含170例样本，其中卵巢癌患者80例，卵巢囊肿患者90例，分析变量（物质浓度峰）共665个。

对上述数据，分别利用KOPLS和OPLS方法对数据进行分析。进行KOPLS分析时，由于变量的数量级变化较大，首先对数据进行标准化，然后建立KOPLS模型。KOPLS使用高斯核函数（σ＝20），通过7折交叉验证选择最大的Q2值，去除3个正交成分时，Q2最大，Q2＝0.314。对数据进行OPLS分析，当去除3个正交成分时，Q2最大，Q2＝0.206（见表1）。从预测成分和第一个正交成分的得分图中（见图6），可以看到OPLS没有将两类很好的分离，而KOPLS的分离效果相对较好。总之，本例使用KOPLS的预测效果和可视化效果都优于OPLS。

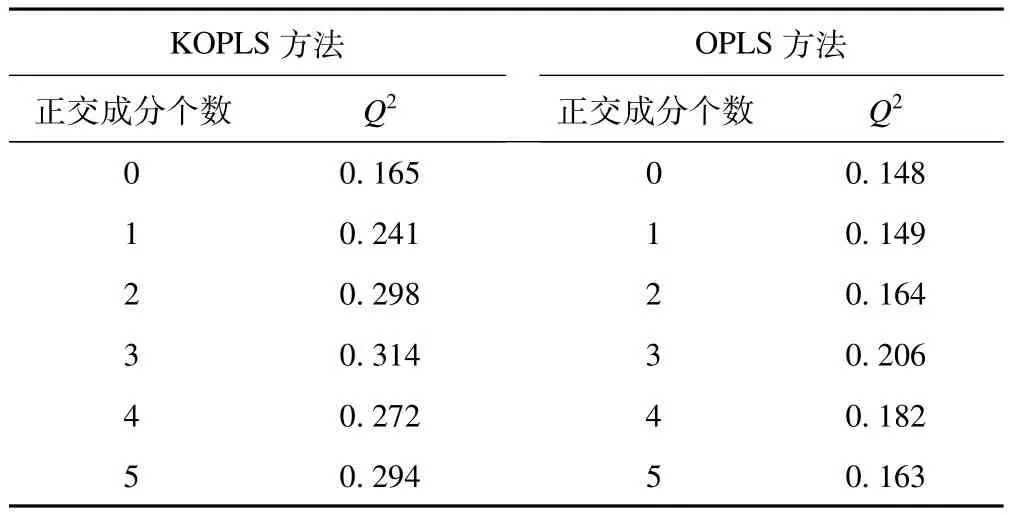
表1 KOPLS和OPLS两种方法的Q2值比较

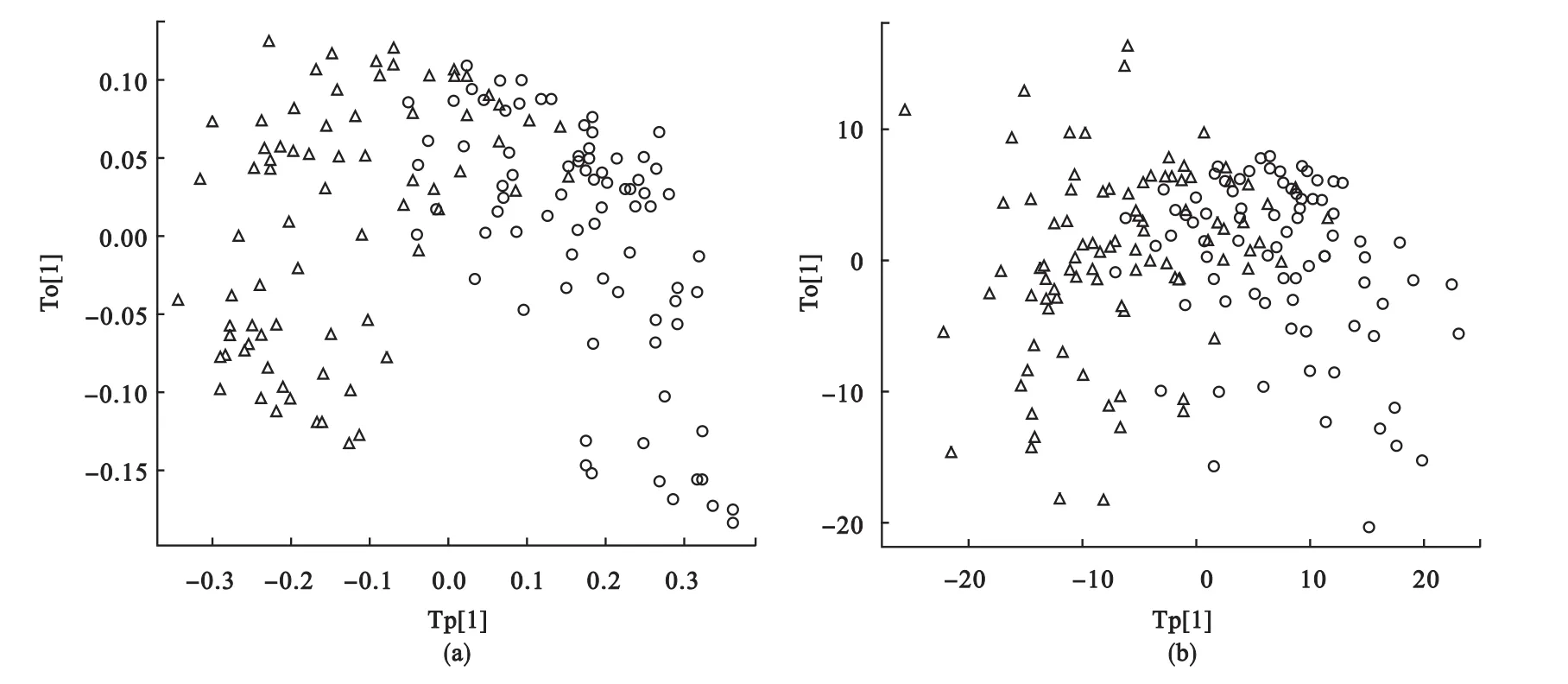
图6 KOPLS方法（a）和OPLS方法（b）的预测成分和第一个正交成分得分图

讨 论

本研究模拟实验表明，当数据间存在线性关系时，应用KOPLS和OPLS两种方法的Q2值和分类可视化效果基本相同，可以任选其中一种方法进行分析。在因变量Y与自变量X之间存在复杂非线性关系情况下，与OPLS模型相比，KOPLS模型的预测能力（Q2）稳健，同时能够保持更合适的可视化效果。通过对实际卵巢癌代谢组学数据的分析，同样显示出KOPLS比OPLS得到的结果更好，说明KOPLS方法可以应用在高维代谢组学数据的分析中。

1.Nguyen D，Rocke DM.Tumor classification by partial least squares using microarray gene expression data.Bioinformatics，2002，18：39-50.

2.Trygg J，Wold S.Orthogonal projections to latent structures（O-PLS）. Journal of Chemometrics，2002，16：119-128.

3.Rosipal R，Trejo LJ.Kernel Partial Least Squares Regression in Reproducing Kernel Hilbert Space.Journal of Machine Learning Research，2001，2：97-123.

4.Rantalainen M，Bylesjo M.Kernel-based orthogonal projections to latent structures（K-OPLS）.Journal of Chemometrics，2007，21：376-385.

5.Czekaj T，Wen W，Beata W.About kernel latent variable approachs and SVM.Journal of Chemometrics，2005，19：341-354.

6.Fonville M，Coen M.Non-linear modeling of 1HNMR metabonomic data using kernel-based orthogonal projections to latent structures optim ized by simulated annealing.AnalyticaChimica Acta，2011，705：72-80.

7.Bylesjo M，Rantalainen M.KOPLS package：Kernel-based orthogonal projections to latent structures for prediction and interpretation in feature space.Bioinformatics，2008，9：106-112.

8.Tao W，Ming Y.Application of Metabolomics in Traditional Chinese Medicine Differentiation of Deficiency and Excess Syndromes in Patients with Diabetes Mellitus.Evidence-Based Complementary and Alternative Medicine，2012.

（责任编辑：郭海强）

The Application of Kernal Orthogonal Projection to Latent Structures（KOPLS）in Metabolomics Data Analysis

Li Junnan，Hou Yan，Li Kang（Department of Medical Statistics，Harbin Medical University（150081），Harbin）

ObjectiveTo explore the characteristics of kernel orthogonal projections to latent structures（KOPLS）method and its application in metabolomics data analysis.MethodsWe use simulated experiment and actual metabolism data to evaluate the prediction ability，classification ability and visualization effect of the KOPLS method.ResultsSimulation experiment and actual metabolomics data analysis proved that when there is a linear relationship between data，the KOPLS has the same effect with traditional linear OPLS methodS.The KOPLS method in dealing with nonlinear relations has higher predictive ability and better classification effect，at the same time，the score of the figure of visual effect is good.ConclusionIt can be applied to high-dimensional omics data analysis better.

Kernel orthogonal projections to latent structures；Non-linear；Metabonomics

*高等学校博士学科专项基金（20122307110004）；国家自然科学基金资助（81172767）

△通信作者：李康，likang＠ems.hrbmu.edu.cn