线荷载作用下的单向板内力分析

吴茜婷 杨 嘉 于 晖

(中国核电工程有限公司，北京 100840)

〗

〗

〗

〗



线荷载作用下的单向板内力分析

吴茜婷 杨 嘉 于 晖

(中国核电工程有限公司，北京 100840)

对实际工程计算时通常将线荷载作用下的单向板按单跨(板)梁来计算主方向上的弯矩，而忽视了次方向上的弯矩，导致板底出现次方向上裂缝的情况作了分析，采用纳维叶解法计算并运用MATLAB绘制了受线荷载作用的单向板，并以长宽比为基本参数，讨论了主次方向上弯矩的变化情况，得出了一些结论。

薄板，纳维叶解法，次弯矩，长宽比

薄板是土木工程中常用的一种构件，钢筋混凝土薄板在建筑和交通工程中应用十分广泛。由薄板的形状以及受力的特点可知，它在弯曲变形时属于空间问题，一般很难获得其精确解，故在分析薄板弯曲问题时多采用弹性力学基本假设外的附加假设(如小挠度理论)。

若矩形板一个方向的长度比另一个方向的长度要大许多，板上的荷载主要向长边传递这样的板在工程上称为单向板。在实际工程中，单向板上作用线荷载的情形有现浇板上砌墙、板(梁)上作用有列车(或车队)荷载等，在设计计算中往往重视主受力方向的弯矩，而容易忽视次方向上的弯矩。但是，在线荷载作用的情形下，次方向上的弯矩一般与主受力方向的弯矩具有相同的量级，甚至还会大于主方向弯矩。本文采用纳维叶解法[2，3]计算并运用MATLAB绘制受线荷载作用的单向板主次方向上的弯矩，并以长宽比为基本参数，讨论了主次方向上弯矩的变化情况。

1 运用纳维叶解法计算弯矩

本文采用纳维叶解法并运用MATLAB研究单向简支板在线荷载作用下的板内弯矩(见图1)，而纳维叶解法是用于解决四边简支矩形薄板的，但当长边b比短边a大许多时(一般是长边比短边大3倍以上)，就可认为是单向板，仍然用纳维叶解法计算主弯矩Mx和次弯矩My。

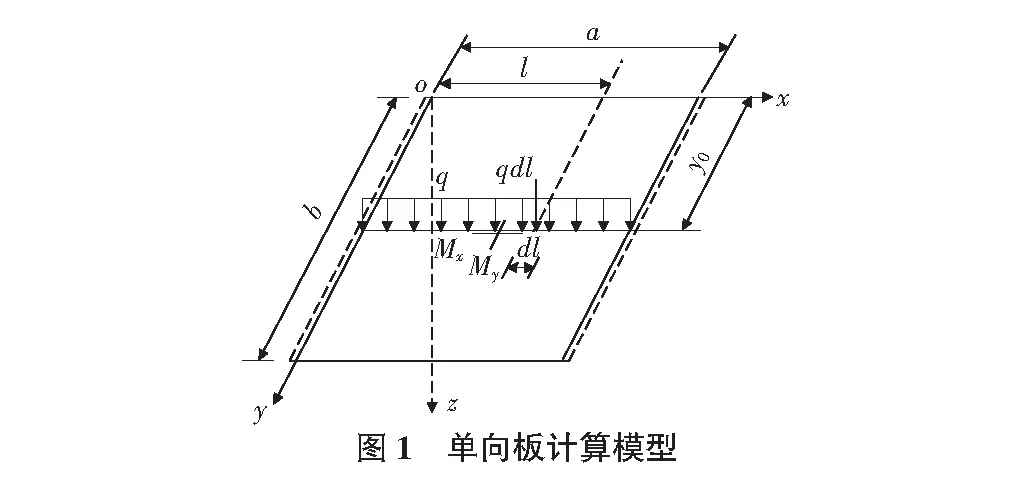
由四边简支且受均布荷载作用的矩形薄板纳维叶解法可推导出受线荷载q作用下在任意一点(x,y)所产生的弯矩：

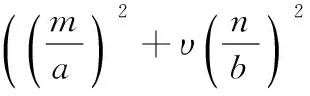
(1)

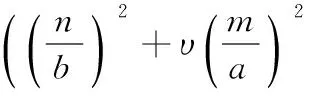
(2)

为了分析方便，将原坐标进行坐标变换，并将长宽比b/a设为参数k，从而得到弯矩计算式为：

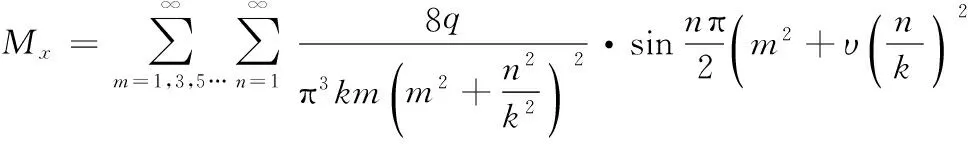
(3)

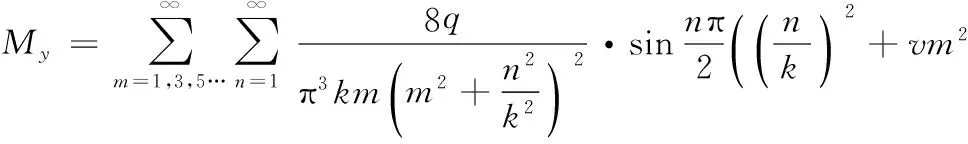
(4)

计算时取υ=0.3,q=10,m=50,n=50。

采用MATLAB可绘制出板内主次弯矩的分布情况。若取长宽比k=3，则板主次截面上的弯矩如图2所示。

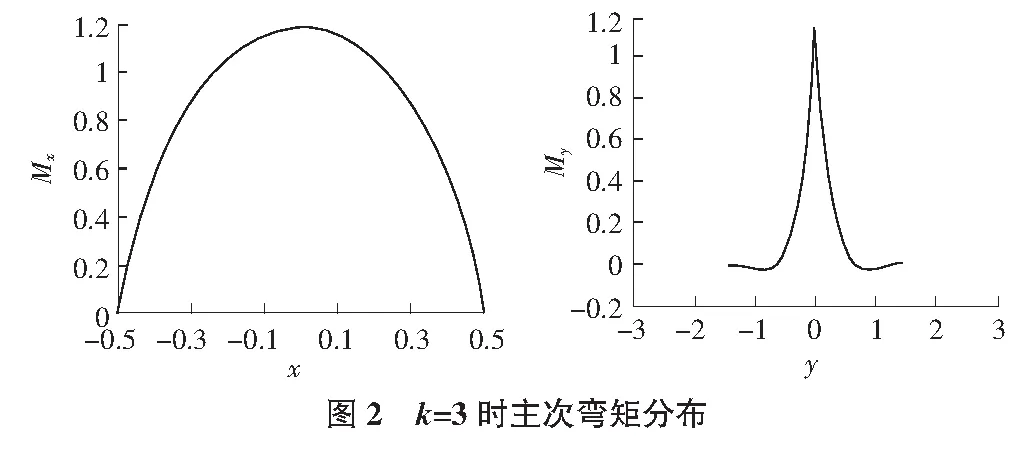
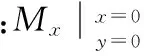
2 参数分析

为了研究主次方向弯矩的比值及Mx，My的大小与长宽比的关系，本文分别研究了Mxm/Mym与k及Mx，My与k两组相互关系。

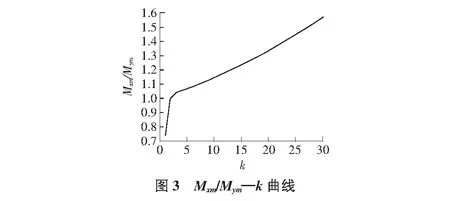
这一相互关系首先说明次方向上的弯矩My与主方向上的弯矩Mx经常是同一数量级的，即使是长宽比很大的情况，My也能达到Mx的1/3，设计时若将My忽略，就有可能在x方向出现水平裂缝；其次说明主次方向上弯矩的比值与板的长宽比是有关联的，在设计时可以考虑长宽比的影响，从而估计My的最大值进行设计，为了安全和设计方便，也可取与Mxm相等的Mym。

另外，k=3，9，30时，分别绘制Mx，My随长宽比k的变化曲线，如图4，图5所示。

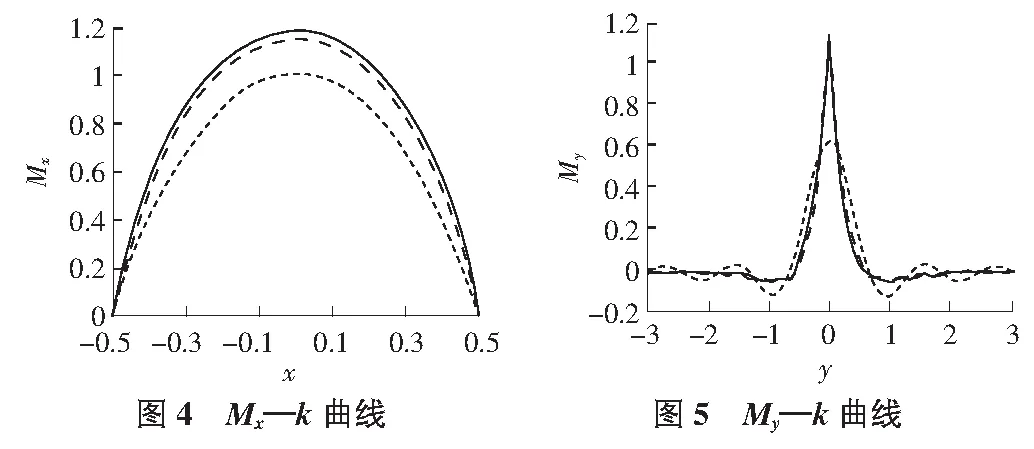
图4，图5中，k=3时的曲线峰值最大，k=9次之，k=30最小，

因此，k越小，则Mx，My的峰值就越大；k越大，则Mx，My的峰值越小；且My的影响范围仅在线荷载作用位置附近一个固定区段，并不随着k的增大而发生明显的变化。

这一结果说明，进行设计时，由于My不可忽略，需要在作用线荷载附近考虑布置y向的钢筋，而钢筋长度的选取，只需考虑这个固定的影响区段的长度及锚固。由于Mx，My随k值的增大而减小，所以设计时应考虑长宽比对弯矩值的影响。

3 结语

本文采用纳维叶解法计算受线荷载作用的单向板的弯矩，并以长宽比为基本参数，讨论了主次方向上弯矩的弯化情况，结论如下：1)随着单向板的长宽的增大，主方向上的弯矩与次方向上的弯矩越来越大，但最终不会超过3.5；2)次方向上的弯矩相对于主方向上的弯矩不可忽略，因此设计中应计算次方向上的弯矩进行配筋；3)主、次方向上的弯矩值会随着长宽比的增大而减小；4)线荷载对次方向上的弯矩影响是在固定的一段区间内的，该区间的长度不会随着长宽比的变化而发生很大的变化。

[1]周克荣，顾祥林，苏小卒.混凝土结构设计.上海:同济大学出版社,2000.

[2]李遇春.弹性力学(土木工程适用).北京:中国建筑工业出版社,2009.

[3]R. Szilard.板的理论和分析.陈太平，戈鹤翔,译.北京：中国铁道出版社,1984.

[4]赵书兰.MATLAB图形与动画编程实例教程.北京:化学工业出版社,2009.

Internal force analysis of one-way slab under linear load

Wu Xiting Yang Jia Yu Hui

(ChinaNuclearPowerEngineeringLimitedCompany,Beijing100840,China)

This paper analyzed calculation of main direction moment of one-way slab as single span(slab), while ignoring the moment in this direction, leading to the cracks situation of slab in secondary direction under linear loads action in actual engineering calculation, using Navier solution calculation and using MATLAB drew the one-way slab under linear loads action, and taking the length to width ratio as the basic parameters, discussed the changes situation of primary and secondary direction moment, gained some conclusions.

thin slab, Navier solution, secondary moment, length to width ratio

1009-6825(2015)01-0052-02

2014-10-28

吴茜婷(1987- )，女，硕士，助理工程师； 杨 嘉(1987- )，女，硕士，助理工程师； 于 晖(1983- )，男，博士，工程师

TU311

A