极化阵列抗主瓣干扰性能研究

罗章凯 王华力 张翼鹏 董文斌

（1.解放军理工大学通信工程学院，江苏 南京210007；2.解放军理工大学通信工程学院，江苏 南京210007；3.南京炮兵学院作战实验中心，江苏 南京211123；4.西昌卫星发射基地，四川 西昌615000）

引 言

自适应波束形成是阵列信号处理的热点问题，被广泛应用于雷达、声纳、通信等领域.传统自使用算法针对旁瓣干扰能取得较好效果，然而当干扰出现在主瓣区域，使用传统自适应算法会引起主瓣畸变、旁瓣电平升高以及阵列最大增益方向偏移等问题［1］.近 年 来，利 用 极 化 敏 感 阵 列（Polarization Sensitive Array，PSA）实现对信号极化域信息和空域信息的接收，将极化域信息和空域信息结合对消主瓣干扰成为新的研究热点［2］.相比于普通阵列（Normal Array，NA），PSA系统稳健性更强，分辨能力更高，抗干扰性能更强，能有效解决仅利用空域信息对消主瓣干扰能力不足的问题.早在20世纪80年代，R.T Compton最先研究了PSA滤波性能［3-5］.多年来国内外学者在该研究领域取得了大量研究成果.例如，王雪松等人［6-7］对极化滤波器性能进行了评估，并讨论了最佳选择的问题.徐振海［8-10］等人对PSA在完全极化情况下和相关干扰条件下滤波性能进行了分析.鉴于极化域滤波的优势，PSA技术近年来发展迅速，开始从理论研究转向工程应用［11-12］.然而PSA的优越性通常是以增加处理维度和系统实现复杂性为代价.为此，文献［13］提出了一种交替极化敏感阵列（Alternant Polarization Sensitive Array，APSA）结构，有效降低了系统复杂性，但抗干扰性能会有所损失.此外，文献［14］研究了特征空间投影算法，文献［15］将其运用到极化域，提高了阵列抗干扰性能稳健性.

为进一步提高APSA的抗主瓣干扰性能，本文将基于特征空间投影算法应用于APSA，并分析比较了APSA和常规PSA在主瓣抗干扰方面的性能.针对期望信号导向矢量存在指向误差情况，进一步讨论了两种阵列对指向误差的稳健性.

1 极化敏感阵列模型

1.1 两种极化阵列导向矢量

PSA是由N个正交偶极子构成的均匀线阵，各阵元沿y轴均匀排列，间距为d，正交偶极子分别沿x轴和y轴放置.APSA是在PSA基础上，交替抽取x方向和y方向的偶极子.如图1所示，两种阵列的阵元数均为N.为了便于研究，对电磁信号、传播介质、噪声和信号独立等条件做理想假设［15］，即不考虑任何非理想因素.

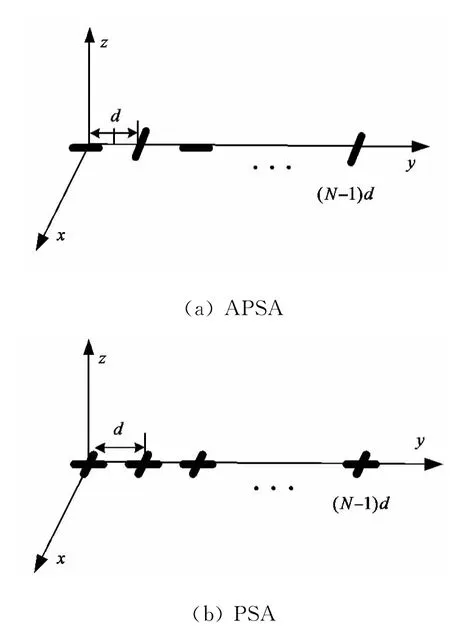
图1 阵列结构示意图

假设一个期望信号和M个互不相关的窄带干扰，空域极化域特征参数为（θkφk，γkηk）.θk，φk分别为方位角和俯仰角，γk，ηk为完全极化波相位描述因子，k＝0，1，…，M.第k个信号PSA导向矢量可表示为

⊗表示Kronecker积.空域导向矢量为

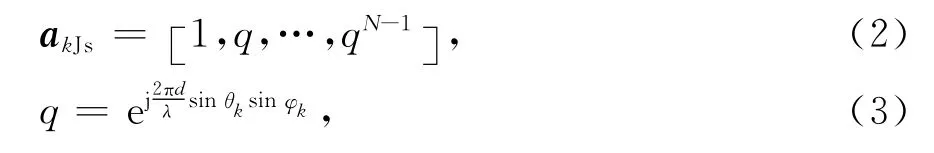
λ为波长.极化域导向矢量为

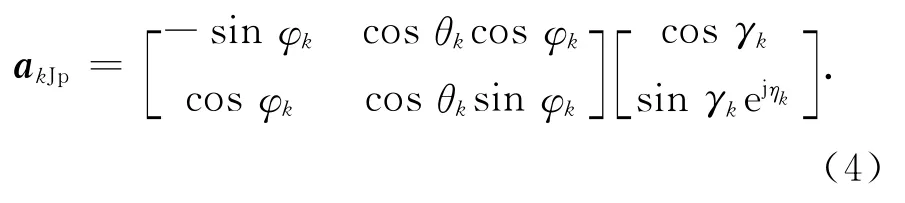
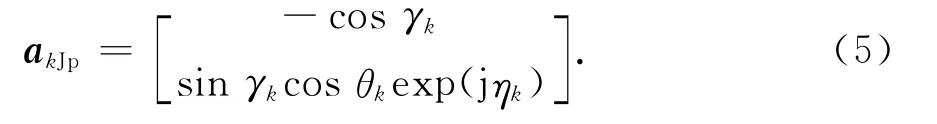
APSA可视为在PSA基础上交替抽取而来，其导向矢量也可表示为空域导向矢量akAs和极化域导向矢量akAp的Kronecker积，即

由图1（a）可见，APSA相同极化阵元间距为2d，那么：

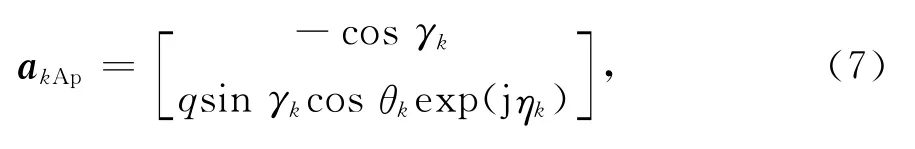
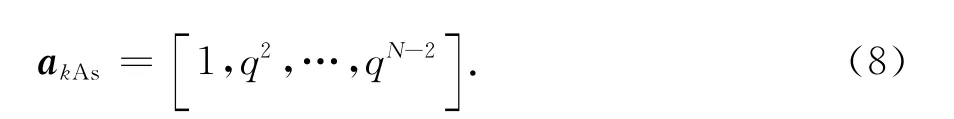
可见，APSA一个阵元处只放置一个极化方向单元，其导向矢量akA维数为N，信号处理维数降低一半.另外由于无需考虑如何在同一位置放置两个单元，阵列实际实现难度低.而PSA导向矢量akJ的维数为2 N.

1.2 接收信号模型

假设有一个期望信号和M个互不相关的窄带干扰，那么通用的阵列接收信号模型为

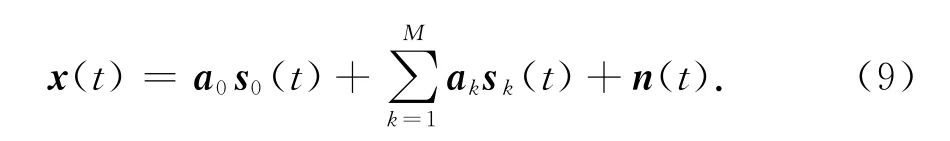
式中：ak为期望信号和干扰信号导向矢量；sk（t）为期望信号和干扰复包络；n（t）为噪声.这里信号模型对NA，PSA以及APSA都适用.对应不同的阵列只需要改变相应导向矢量即可.对于PSA及APSA，ak为空域导向矢量和极化域导向矢量的Kronecker积.

2 算法原理

本文采用的算法基于最小方差准则和特征子空间投影方法，在保证期望信号方向增益同时，最大程度抑制干扰信号和噪声，同时增强期望信号导向矢量存在误差情况下算法的稳健性［15］.

根据最小方差准则，优化问题可表示为

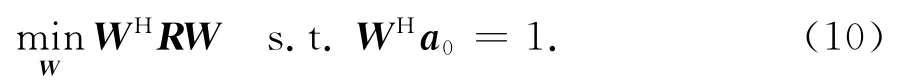
式中：W为权值；R为接收信号协方差矩阵.根据拉格朗日乘数法，得到最优权值为：

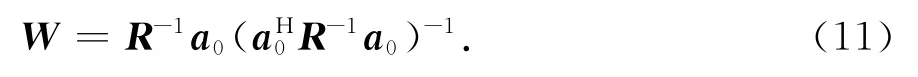
那么加权后输出信号为

在期望信号导向矢量存在失配情况下，为进一步提高算法稳健性，将权值投影到信号子空间，那么式（13）中的权值可表示为

Es为R特征值分解后得到的由期望信号和干扰信号特征矢量组成的信号子空间.

3 极化阵列主瓣抗干扰性能分析

3.1 极化阵列主瓣抗干扰原理

将协方差矩阵R展开，得到

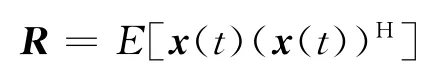
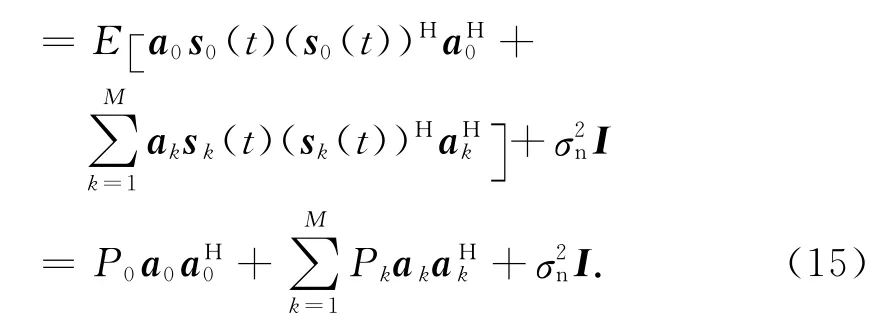
式中：P0＝E［s0（t）（s0（t））H］为期望信号功率；Pk＝E［sk（t）（sk（t））H］为第k个干扰信号功率；为噪声功率.此处将干扰噪声协元方差矩阵表示为则

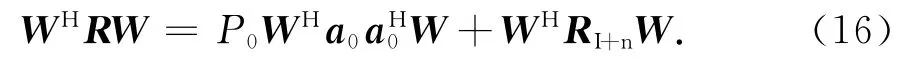
那么阵列输出信干噪比

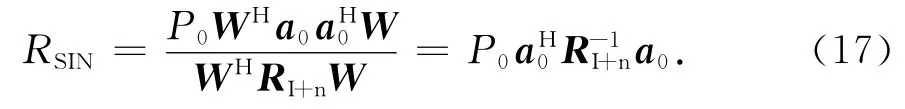
对干扰协方差矩阵RI特征值分解得

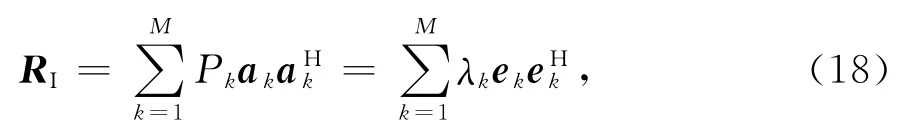
λk和ek代表特征值和相应特征矢量，那么

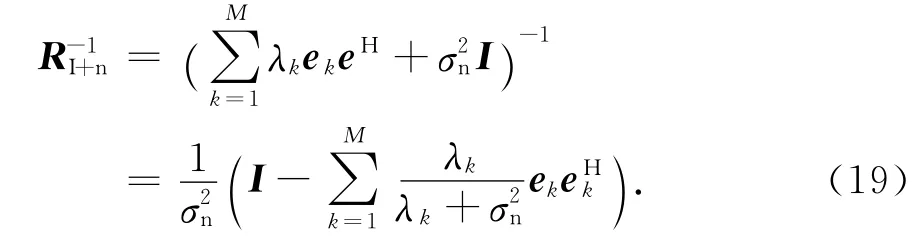
将式（19）代入到式（17）得到

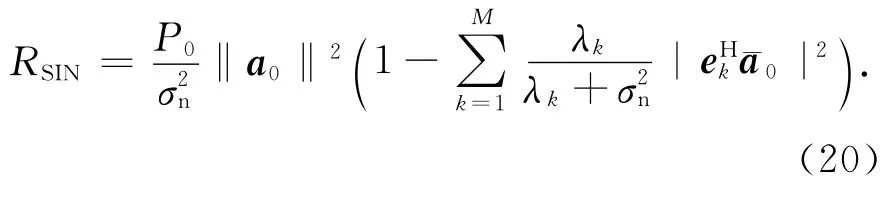
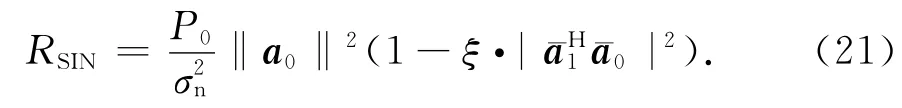
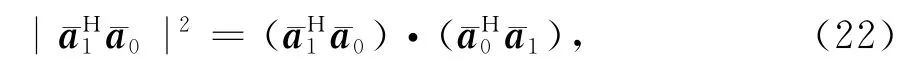
其中

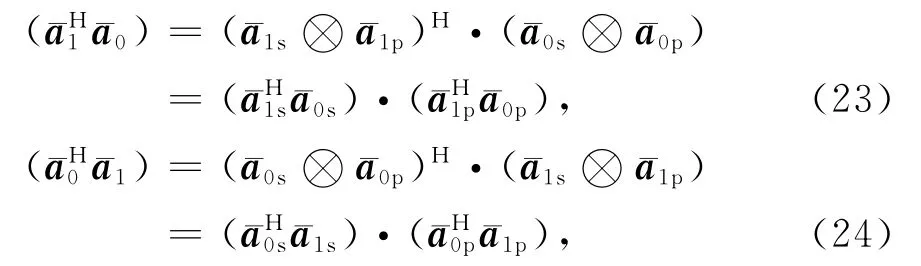
那么

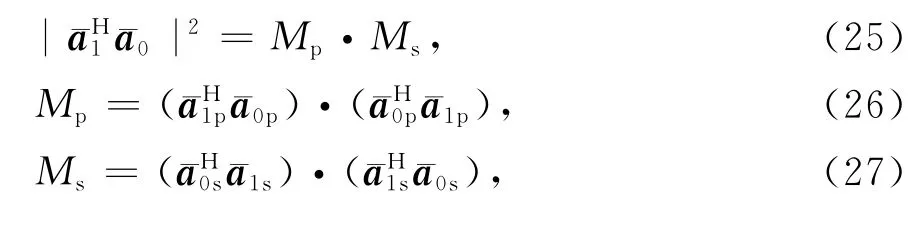
Mp和Ms分别为极化域匹配系数和空域匹配系数.将式（26）和式（27）代入式（21）得输出信干噪比表达式为

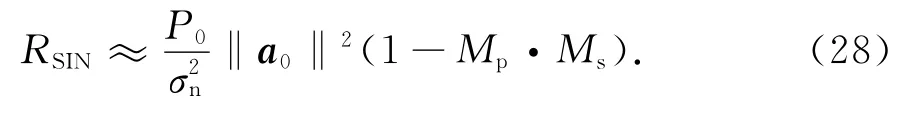
可见，针对主瓣干扰，期望信号和主瓣干扰到达角接近，空域匹配系数接近于1，此时可以通过较小的极化域匹配参数得到较高的输出信干噪比.只有当极化域匹配参数和空域匹配系数均接近于1，主瓣干扰才会影响期望信号的接收.当存在多个干扰时，分析类似.

3.2 两种极化阵列输出信干噪比比较

此处假设阵元间距为半个波长.分别根据式（5）和式（7）对式（26）展开得到PSA极化域匹配系数MJp和APSA极化域匹配系数MAp：

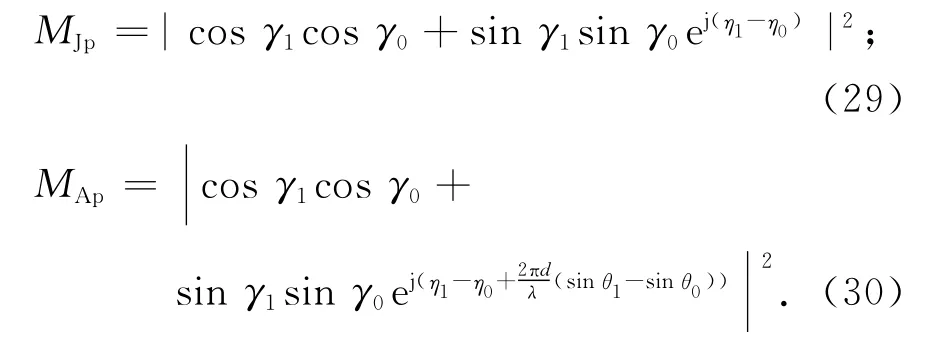
分别根据式（2）和式（8）对式（27）展开得到PSA空域匹配系数MJs和APSA空域匹配系数MAs：

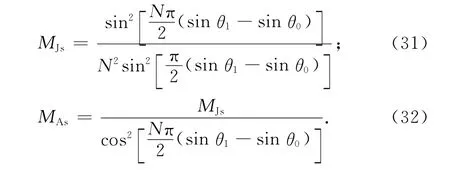
通常情况下，θ0≠θ1，比较式（29）和式（30）可以证明，MAp≥MJp；比较式（31）和式（32）显然可见，MAs≥MJs，当θ0＝θ1时等号成立.所以通常情况下，APSA性能相比于PSA性能略有下降.当干扰与期望信号方位角接近情况下，即θ0≈θ1，可得MJp≈MAp，MJs≈MAs.此时结合式（28）可见，两种阵列输出信干噪比接近相等.

3.3 期望信号导向矢量存在误差情况下算法抗干扰原理分析

在相应阵列（NA、PSA、APSA）基础上，将计算所得权值投影到相应阵列接收信号的协方差矩阵分解所得信号子空间，即

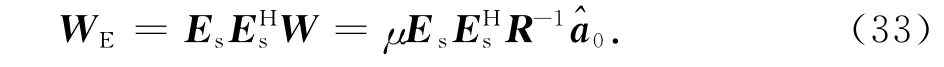
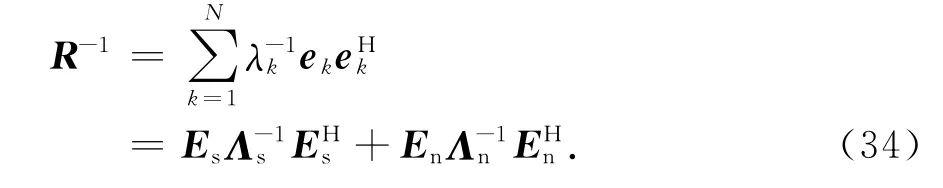
式中：Es＝［e1，e2，…，eM＋1］；En＝［eM＋2，eM＋3，…，λN.Es是根据信号源数目确定的信号子空间，En是对应的噪声子空间，信号子空间与噪声子空间正交.将式（34）代入式（33）得

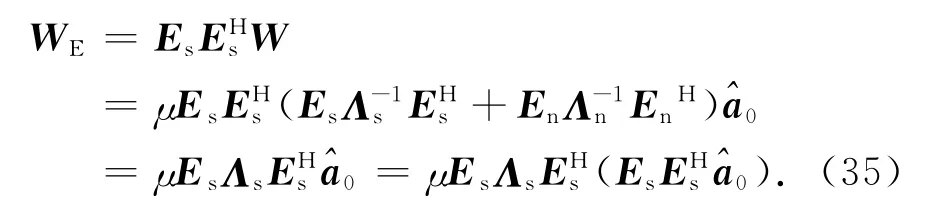
由式（35）可见，将权值投影到信号子空间，等同于将存在失配的期望信号导向矢量投影到信号子空间，只保留了信号子空间分量.当真实的期望信号导向矢量存在信号子空间时，基于投影方法计算所得权值可以一定程度上改善期望信号导向矢量失配的影响.

4 仿真分析

4.1 三种阵列主瓣抗干扰性能比较

仿真采用12元均匀线阵，阵元间距为半个波长.期望信号方位角20°，极化参数γ0＝45°，η0＝180°，信噪比10dB.两个主瓣干扰，干扰方位角分别为19°和21°，极化参数分别为γ1＝30°，η1＝70°，γ2＝60°，η2＝80°.干噪比均为20dB.

比较NA，PSA，APSA主瓣抗干扰性能.图2是三种阵列在信噪比10dB情况下，阵列输出信干噪比曲线.相比于NA，PSA和APSA主瓣抗干扰性能较好，能得到较高的阵列输出信干噪比.

由1.1节两种极化阵列导向矢量分析可知，相比于PSA，APSA通道数减半，系统复杂性降低，信号处理速度更快.图2中，显然基于APSA的信干噪比曲线相比于基于PSA的信干噪比曲线收敛更快.此外，通过3.2节分析可知，通常情况下，APSA性能相比于PSA性能略有下降，即图2中在快拍数为1 024情况下，PSA信干噪比曲线最终收敛点比APSA高.

图3是三种阵列输出信干噪比随输入信噪比变化曲线，快拍数为1 024.APSA相比于PSA输出信干噪比低，这与3.2节理论分析一致.表1给出了基于图3在不同输入信噪比情况下，两种极化阵列输出信干噪比数据.可见APSA相比于PSA输出信干噪比低2～3dB.

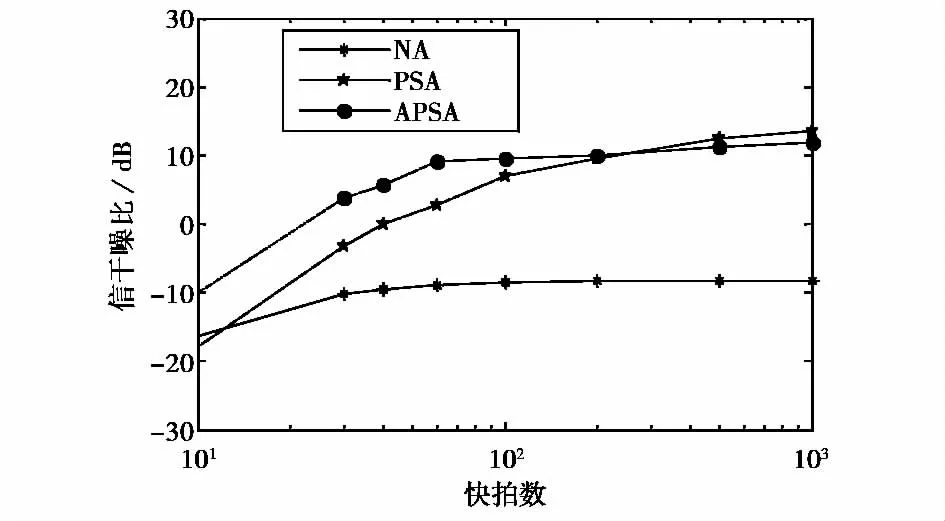
图2 信噪比10dB情况下三种阵列输出信干噪比较

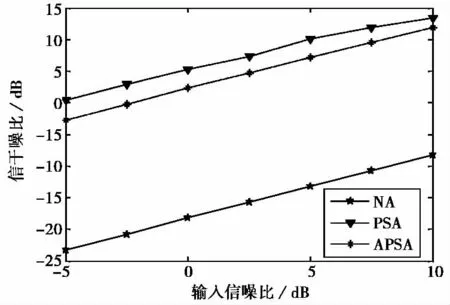
图3 三种阵列主瓣抗干扰性能比较

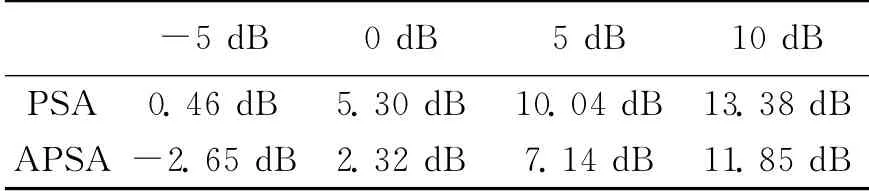
表1 PSA与APSA输出信干噪比比较

4.2 期望信号导向矢量存在误差情况下性能分析

仿真条件如4.1节，不同之处在于期望信号导向矢量存在误差，误差角度范围为-8°～8°，间隔0.5°取值仿真.图4是三种阵列在期望信号导向矢量存在误差情况下，三种阵列主瓣抗干扰性能比较.显然PSA和APSA受期望信号导向矢量误差影响较小.这是由于采用特征空间投影方法，降低了阵列输出信干噪比对期望信号导向矢量误差敏感性.由图4可见，APSA输出信干噪比与PSA输出信干噪比相差不大，当误差角度变大时，信干噪比损失相比于NA也少很多.

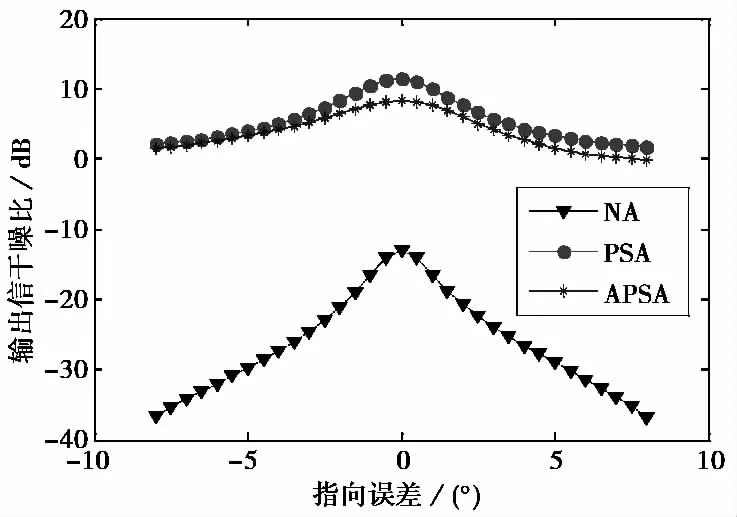
图4 三种阵列性能比较

5 结 论

本文主要研究交替极化敏感阵列主瓣抗干扰性能，并与普通阵列、极化敏感阵列性能作对比.当期望信号导向矢量存在误差时，在三种阵列基础上运用特征空间投影方法，比较三种算法对期望信号导向矢量误差的稳健性.理论分析和仿真结果显示，交替极化敏感阵列既有极化敏感阵列主瓣抗干扰的性能优势，同时其系统复杂度较低，更易于工程实现.鉴于交替极化敏感阵列性能优势，下一步将考虑结合嵌套阵列［16］，进一步提高交替极化敏感阵列抗干扰性能.

［1］王永良，丁前军，李荣锋.自适应阵列处理［M］.北京：清华大学出版社，2009.

［2］庄钊文，徐振海，肖顺平，等.极化敏感阵列信号处理［M］.北京：国防工业出版社，2005.

［3］COMPTON R T Jr.The tri-pole antenna：an adaptive array with a full polarization flexibility［J］.IEEE Transactions on Antennas and Propagation，1981，29（6）：944-952.

［4］COMPTON R T Jr.The Performance of A tri-pole adaptive array against cross-polarized jamming［J］.IEEE Transactions on Antennas and Propagation，1983，31（4）：682-685.

［5］LI J，COMPTON R T Jr.Angle and polarization estimation using ESPRIT with a polarization sensitive array［J］.IEEE Transactions on Antennas and Propagation，1991，39（9）：1376-1383.

［6］王雪松，代大海，徐振海.极化滤波器的性能评估与选择［J］.自然科学进展，2004，14（4）：442-448.WANG Xuesong，DAI Dahai，XU Zhenhai.Performance evaluation and selection of polarization filters［J］.Progress in Natural Science，2004，14（4）：442-448.（in Chinese）

［7］王雪松，汪连栋，肖顺平，等.自适应极化滤波器的理论性能分析［J］.电子学报，2004，32（8）：1326-1329.WANG Xuesong，WANG Liandong，XIAO Shunping，et al.Theoretical performance analysis of adaptive polarization filters［J］.Acta Electronica Sinica，2004，32（8）：1326-1329.（in Chinese）.

［8］徐振海，王雪松，肖顺平，等.极化敏感阵列滤波性能分析：完全极化情形［J］.电子学报，2004，32（8）：1310-1313.XU Zhenhai，WANG Xuesong，XIAO Shunping，et al.Filtering performance of polarization sensitive array：completely polarized case［J］.Acta Electronica Sinica，2004，32（8）：1310-1313.（in Chinese）

［9］徐振海，王雪松，肖顺平，等.极化敏感阵列滤波性能分析：相关干扰情形［J］.通信学报，2004，25（10）：8-15.XU Zhenhai，WANG Xuesong，XIAO Shunping，et al.Filtering performance of polarization sensitive array：correlated interference case［J］.Journal on Communications，2004，25（10）：8-15.（in Chinese）

［10］徐振海，王雪松，冯德军，等.极化域-空域动态联合谱估计［J］.电波科学学报，2005，20（1）：25-28.XU Zhenhai，WANG Xuesong，FENG Dejun，et al.Adaptive estimation for joint spectrum in polarizational and spatial domains［J］.Chinese Journal of Radio Science，2005，20（1）：25-28.（in Chinese）

［11］ZHOU S G，CHIO T H.Dual linear polarization patch antenna array with high isolation and low crosspolarization［J］.IEEE Symposium on AP，2011：588-590.

［12］GUINVARC H R，HAUPT R L.Dual polarization interleaved spiral antenna phased array with an octave bandwith［J］.IEEE Transactions on Antennas and Propagation，2010，58（2）：397-403.

［13］徐振海，张 亮，吴迪军，等.交替极化阵列滤波性能研究［J］.国防科技大学学报，2012，34（5）：49-54.XU Zhenhai，ZHANG Liang，WU Dijun，et al.Filtering performance of alternate polarization array［J］.Journal of National University of Defense Technology，2012，34（5）：49-54.（in Chinese）

［14］YU J L，YEH C C.Generalized eigenspace-based beamformers［J］.IEEE Trans on Signal Processing，1995，43（11）：2453-2461.

［15］郭玉华，常青美，余道杰，等.一种改进的极化域-空域联合的自适应波束形成算法［J］.电子学报，2012，40（6）：1279-1283.GUO Yuhua，CHANG Qingmei，YU Daojie，et al.An improved polarization-space adaptive beamforming algorithm［J］.Acta Electronica Sinica，2012，40（6）：1279-1283.（in Chinese）

［16］PAL P，VAIDYANATHAN P P.Nested arrays：a novel approach to array processing with enhanced degrees of freedom［J］.IEEE Transactions on Signal Process，2010：4167-4181.