碟式太阳能聚光器气动特性和最大风压分布仿真分析

鄂加强,苏秀超,Wenming YANG,王曙辉,刘 腾,左 威

(1. 湖南大学 机械与运载工程学院，湖南 长沙 410082; 2. 新加坡国立大学 机械工程系，新加坡 117576)

碟式太阳能聚光器气动特性和最大风压分布仿真分析

鄂加强1, 2†,苏秀超1,Wenming YANG2,王曙辉1,刘 腾1,左 威1

(1. 湖南大学 机械与运载工程学院，湖南 长沙 410082; 2. 新加坡国立大学 机械工程系，新加坡 117576)

针对碟式太阳能聚光器最佳避风姿势问题，采用流体控制方程建立了碟式太阳能聚光器流场模型，并将计算得到的流场流速和压力再加载耦合到碟式太阳能聚光器前后表面，对碟式太阳能聚光器气动特性和风压分布进行仿真分析.结果表明：①风速对碟式太阳能聚光器表面中心区域最大风压影响很大，应适当提高碟式太阳能聚光器中心处的强度和刚度；②碟式太阳能聚光器的升力、阻力、侧向力和最大表面风压随风速增加而增加，且最大表面风压增加幅度尤显明显，但是风力系数随风速变化甚微；③不考虑流固耦合作用时碟式太阳能聚光器的升力系数、阻力系数、侧向力系数和最大表面风压的计算值存在较大的误差，在之后的计算中，应考虑流固耦合作用；④碟式太阳能聚光器表面最大风压随高度角和方位角的变化复杂，高度角为0°、方位角为45°姿势时达到最大.

聚光器；虚拟风洞实验；气动特性；太阳能；流固耦合

太阳能作为可再生能源与传统能源相比适用范围广且效益显著[1]，并拥有广阔的发展前景[2].对于碟式太阳能聚光器而言，风的扰动作用是最大的不确定载荷，而影响碟式太阳能聚光器气动载荷的最重要部位即是反射面.聚光器是一种在刚性金属结构支持下跟踪太阳的反射镜，由控制系统进行方位和角度的调整，然而太阳能发电系统往往都位于空旷的平整场地，大气流动对于聚光器所产生的风力作用较大，所以对于聚光器在风荷载作用下的风压研究就显得尤为重要.目前有关表面风压的研究多集中于高层、大跨、低矮房屋等结构上[3-6]，且关于碟式太阳能聚光器的研究主要集中在提高吸热器能量转化效率[7-10]、聚光器聚光效率[11-13]等方面，李正农教授曾使用风洞试验的方法对太阳能定日镜体型系数进行研究以实现对定日镜结构进行抗风设计和定日镜受风作用时的风振相应的分析[14-15]，而对于碟式太阳能聚光器这样特殊体型的结构的风荷载研究非常少.风洞试验是常用的计算结构风载荷的方法，成本高、周期长，而数值仿真方法可以快速准确地得到模型受风作用时的模型风效应情况，避免了风洞试验由于忽略细节而引起的计算误差，从而显示出蓬勃生机[16-18].国内外学者也提出过多种风载荷计算方法[19-21].

因此，本文采用简化的物理模型和高精度的数值算法，对处于恒风速虚拟风洞实验下的碟式太阳能聚光器进行气动载荷分析，获得碟式太阳能聚光器气动载荷分布，为改进碟式太阳能聚光器的结构以及对工程实践中的最佳避风姿势问题提供理论依据.

1 基于虚拟风洞实验的碟式太阳能聚光器仿真模型

1.1 碟式太阳能聚光器物理模型

碟式太阳能聚光器三维简化模型主要包括底座、平衡块、支架、聚光器、悬臂梁、接收器等.本文仅就聚光器表面风压进行分析研究，因此抽取出聚光器模型，该模型直径为17 m，厚度为27 mm，在建模过程中即建好不同工况下的16个模型(由高度角α和方位角β体现)，如图1所示.

图1 聚光器三维简化模型

碟式太阳能发电系统聚光器直径约为17 m，厚度为0.027 m，为保证气流在流体域内的流动达到充分发展的状态，流体域的长度尺寸约为碟式太阳能发电系统聚光器尺寸的10倍，流体域的宽度和高度约为聚光器尺寸的5倍，经过多次建模仿真，确定流体域的尺寸为170 m×80 m×80 m，模型中心距地面高度为10 m，风的入口距模型中心距离为55 m，如图2所示.

图2 聚光器流场网格及加密区域

对模型进行设定，将空气看作连续介质、无压缩粘性流体.网格的类型和数量对计算结果的准确性具有很大的影响.对该模型的流体区域采用的是多面体网格，非结构网格具有很好的灵活性和适应性，易于进行网格自适应.为了更准确地模拟聚光器周围流场特性，对聚光器周围区域有远及近逐步加密.

1.2 碟式太阳能聚光器风荷载数学模型

由于风载作用于碟式太阳能聚光器是瞬时的不稳定的载荷，在分析中不能忽略结构的惯性，就必须采用动态分析.为分析问题方便，不妨以下标f表示流体，下标s表示固体.

1.2.1 流体控制方程

流体流动要遵循物理守恒定律，基本的守恒定律包括质量守恒定律、动量守恒定律、能量守恒定律.如果流体中包含混合的其他成分，系统还要遵循组分守恒定律.对于一般的可压缩牛顿流来说守恒定律通过如下控制方程描述.

质量守恒方程：

(1)

式中τ为时间，s；为哈密顿算子，=(∂/∂x)i+(∂/∂y)j+(∂/∂z)k；ρf为流体密度，kg/m3，v为流体速度，m/s.

动量守恒方程：

(2)

式中ff为体积力，kg/(m2·s2)；τf为剪切力，Pa，可表示为：

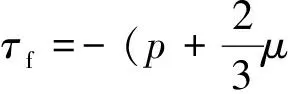
(3)

式中p为流体压强，Pa；μ为动力粘度，Pa·s；I为单位张量；e为速度应力张量，e=(▽v+▽vT)/2.

1.2.2 固体控制方程

固体质量守恒方程：

(4)

式中ρs为固体密度;σs为柯西应力张量，Pa；fs为体积力，kg/(m2·s2)；ds为固体域当地位移，m.

上述流体和固体控制方程都没有考虑能量方程，若考虑流体、固体的能量传递，需要添加能量方程，对于流体部分总焓htot形式的能量方程可以写成如下形式：

▽·(v·τf)+v·ρff+SE

(5)

式中λ为导热系数，W/(m·K)；SE为能量源项，W.

1.2.3 流固耦合方程

在流固耦合的区域，风载荷对碟式太阳能聚光器的压力可改变碟式太阳能聚光器的变形量，而后者反过来又会影响碟式太阳能聚光器上下游的气流流速和压力的分布.故将计算得到的碟式太阳能聚光器流场流速和压力再加载到聚光器的前后表面，并对流体控制方程和固体控制方程进行耦合求解.

碟式太阳能聚光器流固耦合遵循最基本的守恒原则，所以在流固耦合交接面处，应满足流体应力τf与固体应力τs、流体位移df和固体位移ds、流体热流量qf和固体热流量qs、流体温度Tf和固体温度Ts等变量相等，即满足如下4个方程：

(6)

式中nf为流固耦合交接面处流体法向单位矢量；ns为流固耦合交接面处固体法向单位矢量.

1.3 碟式太阳能聚光器风力分析

风力N与流体密度ρ、流速v、流体的粘性μ、碟式太阳能聚光器的主要尺寸D有关，故风力N可表示为：

(7)

用因式分解法可得：

(8)

因为碟式太阳能聚光器的主要尺寸D2正比于碟式太阳能聚光器的特征面积A(即D2∝A)，雷诺数Re=ρvD/μ，故式(8)可表示为：

N=0.5ρv2ACF

(9)

式中CF为风力系数，CF=f(Re).

因此，碟式太阳能聚光器表面风压载荷可表示为：

p=0.5ρv2CF

(10)

如图3所示，将总风力进行分解，得到不同工况下升力NL、阻力ND、侧向力NC，升力系数CL、阻力系数CD、侧向力系数CC的计算公式如下：

(11)

(12)

(13)

式中ρ为空气密度，ρ=1.184 15 kg/m3;v为风速;A为聚光器在迎风面的面积.

对于同一个物体，当风向不同时，风力也不同，但为了计算方便，无论风向如何，公式中的A要取一个相同值，本文中总取聚光器高度角为0°、方位角为0°时的最大面积A=222.510 2 m2.β为聚光器高度角，α为聚光器方位角.

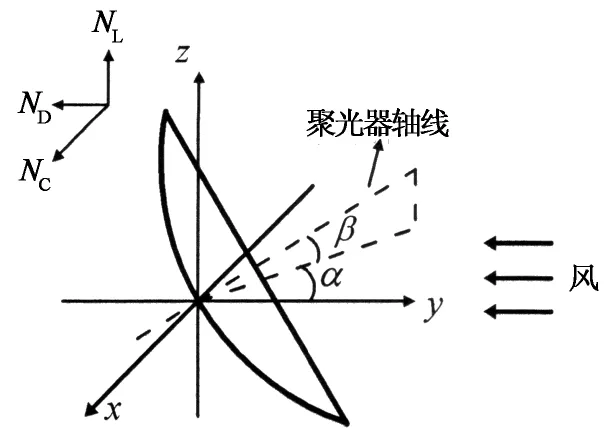
图3 碟式太阳能聚光器受力图

1.4 碟式太阳能聚光器仿真条件设定

设置边界条件之前需对模型的流体域进行设置，流体域中所选流体为空气，气温为常温且绝热，参考压强为1标准大气压，所选的湍流模型为标准的κ-ε模型，在该流体域内设置边界条件.对该计算流体而言，通过模拟风洞实验的方式，采用3种初始条件和边界条件．

1)入口初始条件和边界条件：该区域的流体为不可压缩流体，入口初始风速分为恒定风速，流体流动为不可压缩流体流动，入口风速v=15 m/s,v=20 m/s和v=25 m/s.

2)出口边界条件：出口处的边界条件采用压力出口边界条件，压强为一个标准大气压.

3)壁面条件：流体域表面和聚光器表面，wall是一种限定流体域和固体域的边界条件.壁面条件的粗糙度设置为光滑.对于粘性流体，采用粘附条件，即认为壁面处流体速度与壁面该处的速度相同，无滑移壁面的速度为零，壁面处流体速度为零.聚光器表面和地面是固定不动，不发生移动的，所以采用无滑移的壁面条件；而流体域的顶面和前后面采用滑移边界条件.

对碟式太阳能聚光器流体域进行数值模拟时，不考虑热交换，即不考虑能量方程.因为流体介质是空气，具有不可压缩性，密度为常数.

1.5 碟式太阳能聚光器流体域流固耦合求解

碟式太阳能聚光器流体域流固耦合求解流程如图4所示.具体求解步骤如下：

Step1 利用CFD软件求解碟式太阳能聚光器表面所受平均风压pe1和最大风压pmax1；

Step2 利用静力计算程序确定结构在平均风压pe1和最大风压pmax1作用下的平均变形量δe1和最大变形量δmax1，此时碟式太阳能聚光器表面变形会导致碟式太阳能聚光器表面风力系数发生变化；

Step3 在平均变形量δe1和最大变形量δmax1的基础上，再次利用CFD软件求解碟式太阳能聚光器表面的平均风压pe2和最大风压pmax2；

Step4 利用静力计算程序确定结构在平均风压pe2和最大风压pmax2作用下的平均变形量δe2和最大变形量δmax2；

Step5 如果δe1≈δe2，平均风压pe2就是与碟式太阳能聚光器表面平均变形对应的平均风压，否则重复Step1～4，继续求解δei及其对应的平均风压pei，直到δe(i-1)≈δei为止.此时平均风压pei就是与碟式太阳能聚光器表面平均变形对应的平均风压.

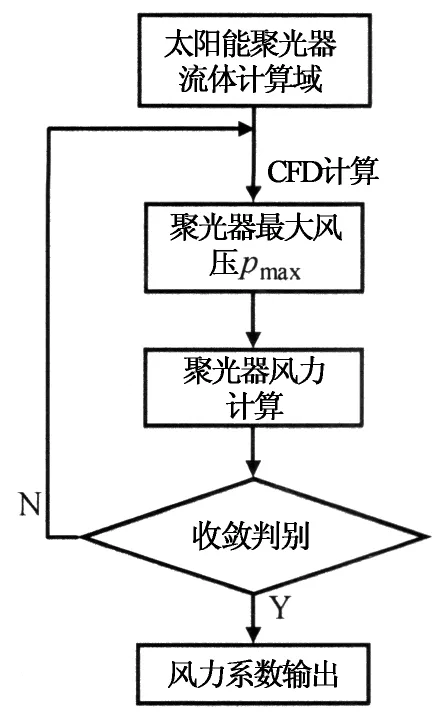
图4 碟式太阳能聚光器流体域流固耦合求解流程

2 基于虚拟风洞实验的碟式太阳能聚光器气动特性和风压分布仿真分析

基于碟式太阳能聚光器模型在风场中遵循的各项理论，对其进行风场数值仿真模拟实验.影响碟式太阳能聚光器流场特性的因素有多种，其中影响程度较大的主要有风速v、聚光器高度角β、方位角α(风向角本也是其影响因素之一，但本文中将风向角转变为碟式太阳能聚光器的方位角来考虑).考虑到碟式太阳能聚光器工作的多工况性，本文选取3种常见典型风速(15 m/s,20 m/s,25 m/s)、4种不同高度角(0°,30°,60°,90°)和5种不同方位角(0°,45°,90°,135°,180°)进行组合所得到的48种工况，然后针对这48种工况对碟式太阳能聚光器气动特性和风压分布进行仿真分析.

2.1 碟式太阳能聚光器压强分布影响分析

高度角为0°、方位角为0° 时，碟式太阳能聚光器反射面压强分布云图如图5所示.由图5可以得知，当碟式太阳能聚光器计算域入口风速由v=15 m/s不断增大到v=25 m/s时，碟式太阳能聚光器反射面受到的压强也随之增大，且碟式太阳能聚光器中心区域的风压较大，而远离中心区域的风压较小，这是由于风载荷作用于碟式太阳能聚光器表面时，风向碟式太阳能聚光器的中心聚焦，而在碟式太阳能聚光器边缘出现脱离，而且在风速增大过程中，高压区有不断扩大且上移的趋势，应适当提高碟式太阳能聚光器中心处的强度和刚度.

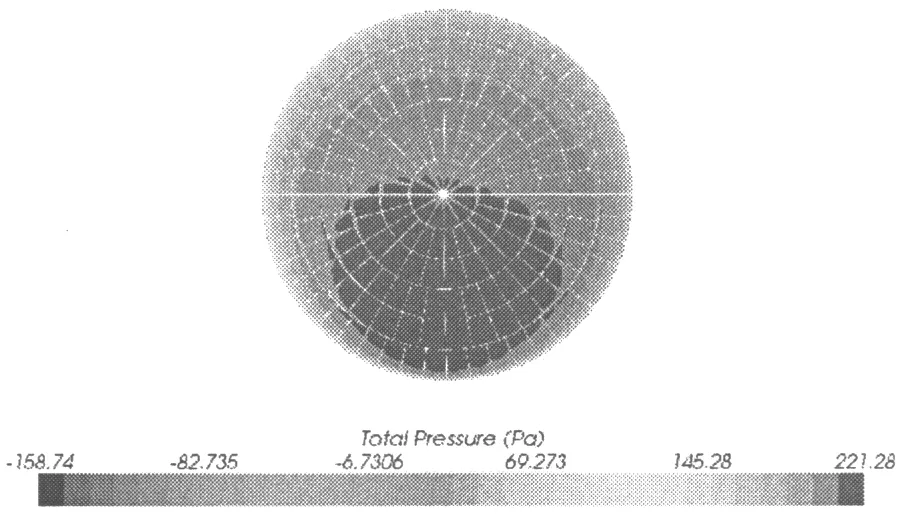
(a) v=15 m/s

(b) v=20 m/s

(c) v=25 m/s

碟式太阳能聚光器在相同高度角与恒定风速下反射面压强随方位角变化的分布云图如图6所示.由图6可以得知，当恒定风速为15 m/s时，不同姿态下的碟式太阳能聚光器的压力分布不同，在高度角β=0°和方位角α=0°时，碟式太阳能聚光器中心区域的风压较大，而远离碟式太阳能聚光器中心区域的压力较小，这是由于风载荷作用于碟式太阳能

聚光器时，风载荷向碟式太阳能聚光器中间聚集，而在碟式太阳能聚光器边缘出现脱离；聚光器在靠近来流方向的位置压力较大，而远离来流方向，压力相对较小.当改变恒定风速为20 m/s或25 m/s时，碟式太阳能聚光器在高度角β=0°时反射面压强相应增加，但其随方位角变化趋势与如图6基本相似.

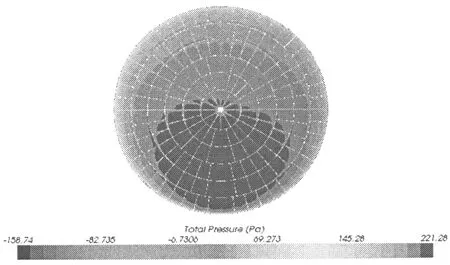
(a) α=0°

(b) α=45°

(c) α=90°

(d) α=135°

2.2 碟式太阳能聚光器气动特性分析

得到不同工况下碟式太阳能聚光器的升力系数、阻力系数、侧向力系数和最大表面风压分别如表1所示.

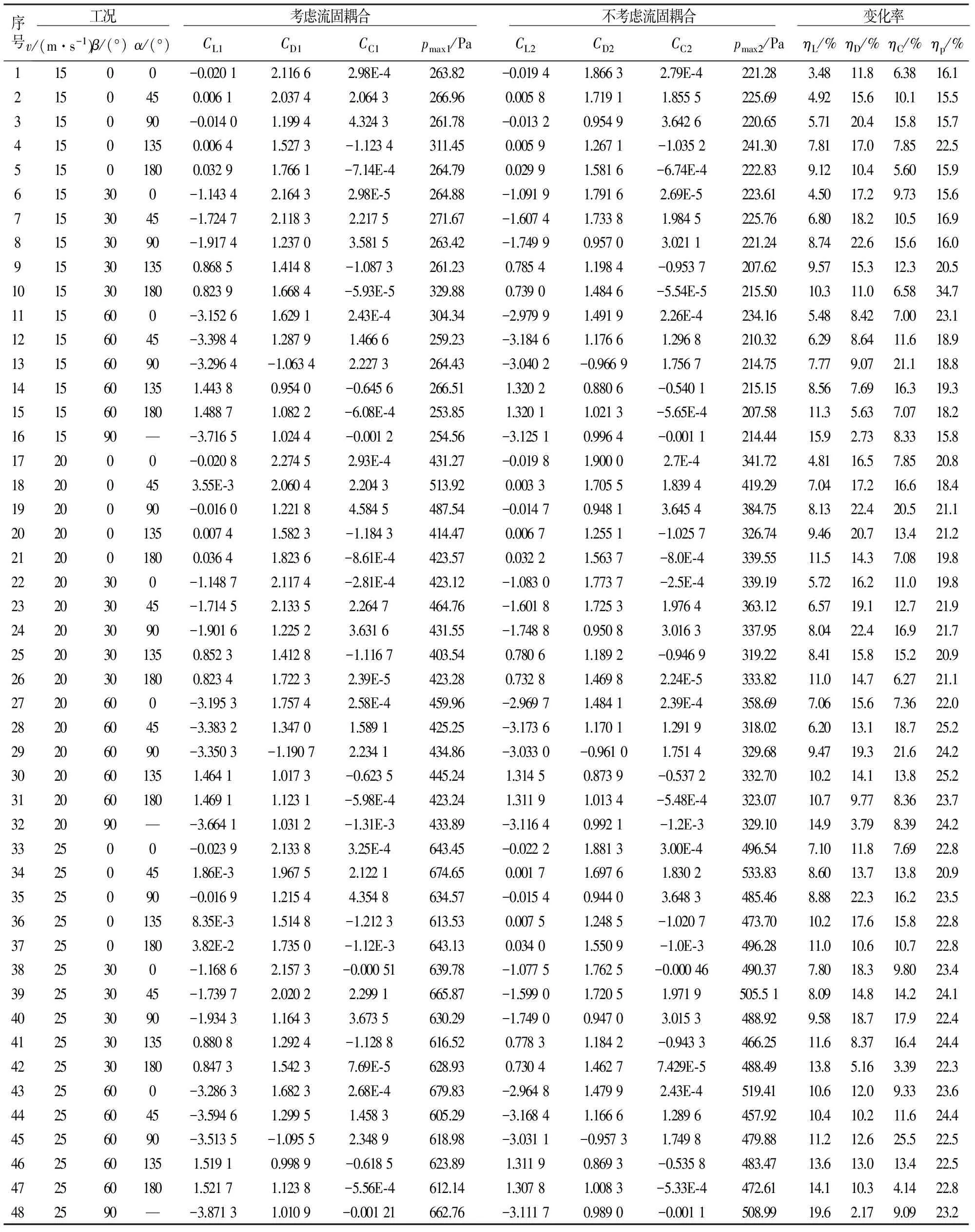
表1 不同工况下聚光器迎风面最大风压和风力系数

由于碟式太阳能聚光器升力来源于聚光器的上、下表面的压力差，阻力来源于聚光器的前、后表面的压力差，而侧力则来源于聚光器的左、右表面的压力差.

当碟式太阳能聚光器的高度角和方位角均为0°时，碟式太阳能聚光器有效迎风面积最大，相比于其他姿态，其表面峰值压力增大，并在背风区形成的空气负压区压力绝对值增大，压强差的增大也就造成碟式太阳能聚光器阻力的增大.在相同的风速下，随着高度角的增加，碟式太阳能聚光器前后表面空气流场的相互干扰，使碟式太阳能聚光器迎风面流动受阻，负压绝对值峰值增大，碟式太阳能聚光器前后表面的压力差形成背风面分离涡，导致碟式太阳能聚光器的升力随之相应增大.而当方位角为0°、高度角为90°时，聚光器受侧向力最大，此时聚光器凹面正朝上方，风从正侧面吹来，侧向力最大.

随着风速的增加，碟式太阳能聚光器的升力、阻力、侧向力和最大表面风压也随之增加，且最大表面风压增加幅度尤显明显；然而风力系数只与物理的形状和雷诺数Re有关，该模型的数值模拟结果表明，不同的风力系数大小有别，但是各自随风速的变化甚微，在一定程度上可忽略其变化.表1表明，当不考虑流固耦合作用时，碟式太阳能聚光器的升力系数CL2,阻力系数CD2,侧向力系数CC2和最大表面风压pmax2明显地小于考虑流固耦合作用时的碟式太阳能聚光器的升力系数CL1,阻力系数CD1和侧向力系数CC1以及最大表面风压pmax1，不考虑流固耦合作用时碟式太阳能聚光器的升力系数变化率ηL、阻力系数变化率ηD、侧向力系数变化率ηC和最大表面风压变化率ηp的最大值分别为19.6%,22.6%,25.5%和34.7%，其最小值分别为3.48%,2.73%,3.39%和15.5%.显然，不考虑流固耦合作用时，会给碟式太阳能聚光器的升力系数CL,阻力系数CD,侧向力系数CC和最大表面风压pmax的计算带来较大的误差.

2.3 碟式太阳能聚光器表面最大风压变化分析

由于最大风压往往只是出现在某个点位置，所以用曲线图表示最大风压的变化趋势更加直观.碟式太阳能聚光器表面最大风压随方位角、风速和高度角的变化趋势曲线图分别如图7,图8和图9所示.

由图7可以得知，当碟式太阳能聚光器计算域入口风速不断增大时，碟式太阳能聚光器表面最大风压pmax也随之增大.风速不同、相同高度角下聚光器表面最大风压随方位角的变化趋势相同.当β=0°和β=30°时，最大风压呈现随方位角的增加而先增后减再增的趋势；β=60°时，最大风压呈现随方位角的增大先减后增再减的变化趋势；当β=90°时，碟式太阳能聚光器凹面正向上，方位角并不改变其姿态，表面最大风压pmax不随方位角的变化而变化，其值只由风速的大小所决定.图7表明，当风速由v=15 m/s分别增加为v=20 m/s,v=25 m/s时，其最大风压分别增加了53.5%和137.4%.

α/(°)

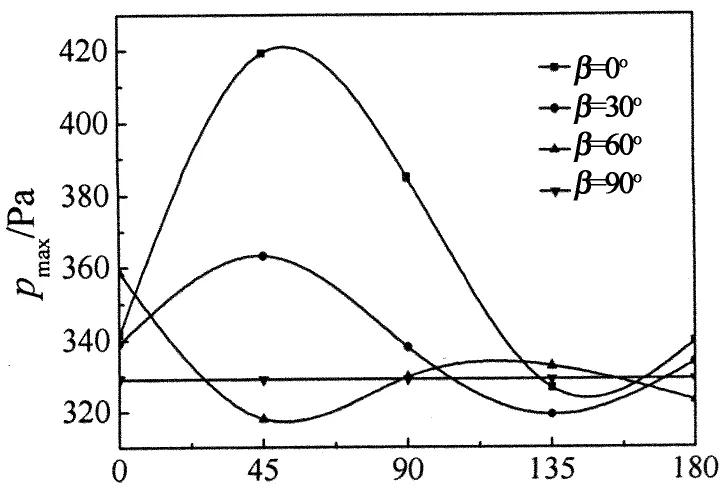
α/(°)

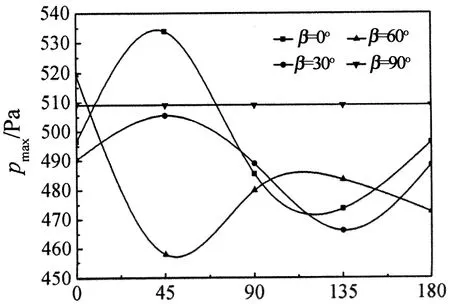
α/(°)

由图8可以得知，不同高度角下的碟式太阳能聚光器表面最大风压pmax曲线随计算域入口风速v的增加呈现近似线性增加的趋势.计算域入口风速v较小时，高度角和方位角对碟式太阳能聚光器反射面受到的最大压强pmax影响都较小.当计算域入口风速v>20 m/s后，方位角不同使得聚光器表面最大风压有所差别，且表面最大风压随风速升高的增大幅度稍有所增加.当高度角β和计算域入口风速v相同时，方位角α=90°时的碟式太阳能聚光器表面最大风压pmax为最大，方位角α=135°时的碟式太阳能聚光器最大风压pmax为最小，这主要是因为方位角α=90°时作用于碟式太阳能聚光器法向风载荷较大，而方位角α=135°时作用于碟式太阳能聚光器法向风载荷较小的缘故.

v/(m·s-1)

v/(m·s-1)

如图9所示，不同风速时，聚光器表面最大风压随高度角的变化趋势并不完全相同，这主要是因为高度角改变使得流场更加复杂化，致使风速增加不仅仅使流场的各强度和现象增强，而有可能使流场某些位置发生质的改变.方位角是0°时，随高度角增大，最大风压pmax呈先增后减的变化趋势；风速增大会使这种变化趋势更明显；其他工况下，风速和方位角不变时，最大风压pmax呈现随高度角的增加而先减后增的趋势，而且风速的增大会使这种变化趋势更加明显.

β/(°)

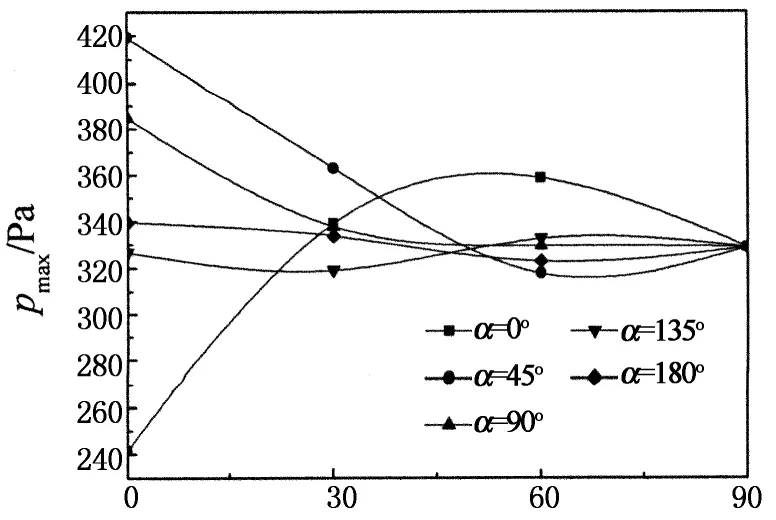
β/(°)

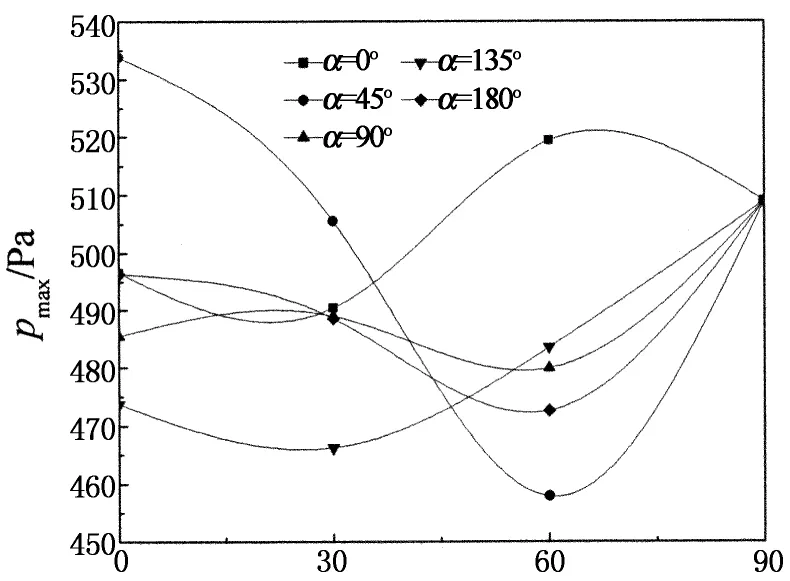
β/(°)

3 结 论

1)碟式太阳能聚光器表面中心区域存在最大风压区域，且随着风速的增大而不断增加，应适当提高碟式太阳能聚光器中心处的强度和刚度.

2)随着风速的增加，碟式太阳能聚光器的升力、阻力、侧向力和最大表面风压也随之增加，且最大表面风压增加幅度尤显明显，但是风力系数随风速变化甚微.

3)不考虑流固耦合作用时碟式太阳能聚光器的升力系数变化率ηL、阻力系数变化率ηD、侧向力系数变化率ηC和最大表面风压变化率ηp的最大值分别为19.6%,22.6%,25.5%和34.7%，其最小值分别为3.48%,2.73%,3.39%和15.5%.

4)碟式太阳能聚光器表面最大风压随高度角和方位角的变化复杂，高度角为0°,方位角为45°姿势时达到最大.

[1] KALOGIROU S A. Solar thermal collectors and applications[J]. Progress in Energy and Combustion Science, 2004, 30(8): 231-295.

[2] SARDESHPANDE V R, CHANDAK A G, PILLAI I R. Procedure for thermal performance evaluation of steam generating point-focus solar concentrators[J]. Solar Energy, 2011, 85(7): 1390-1398.

[3] BECKER S, LIENHART H, DURST F. Flow around three-dimensional obstacles in boundary layers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(4/5): 265-279.

[4] IKHWAN M, RUCK B. Flow and pressure field characteristics around pyramidal buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(10): 745-765.

[5] UEMATSU Y. Wind loads on free-standing canopy roofs: Part 1 local wind pressures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7): 1015-1028.

[6] UEMATSU Y. Wind loads on free-standing canopy roofs: Part 2 overall wind forces[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7): 1029-1042.

[7] WU S Y, XIAO L, CAO Y D,etal. Convection heat loss from cavity receiver in parabolic dish solar thermal power system: a review[J]. Solar Energy, 2010, 84(8): 1342-1355.

[8] REDDY K S, SENDHIL Kumar N. Combined laminar natural convection and surface radiation heat transfer in a modified cavity receiver of solar parabolic dish[J]. International Journal of Thermal Science, 2008, 47(12): 1647-1657.

[9] SENDHIL K N, REDDY K S. Numerical investigation of natural convection heat loss in modified cavity receiver for fuzzy focal solar dish concentrator[J]. Solar Energy, 2007, 81(7): 846-855.

[10]ZANGANEH G, BADER R, PEDRETTI A. A solar dish concentrator based on ellipsoidal polyester membrane facets[J]. Solar Energy, 2012,86(1): 40-47.

[11]XIAO J, WEI X D, LU Z W,etal. A review of available methods for surface shape measurement of solar concentrator in solar thermal power applications[J]. Renewable and Sustainable Energy Reviews, 2012, 16(5): 2539-2544.

[12]HERNANDEZ N, RIVEROS-ROSAS D, VENEGAS E,etal. Conical receiver for a paraboloidal concentrator with large rim angle[J]. Solar Energy, 2012，86(4):1053-1062.

[13]JOSÉ Ruelas, NICOLS Velázquez, JESS Cerezo. A mathematical model to develop a scheffler-type solar concentrator coupled with a stirling engine[J]. Applied Energy, 2013, 101(1): 253-260.

[14]宫博，李正农，王莺歌，等. 太阳能定日镜结构风载体型系数风洞试验研究[J]. 湖南大学学报:自然科学版, 2008, 35(9):6-9.

GONG Bo, LI Zheng-nong, WANG Ying-ge,etal. Wind tunnel test study on the wind load shape coefficient of heliostat[J].Journal of Hunan University:Natural Sciences, 2008,35(9):6-9.(In Chinese)

[15]宫博，李正农，吴红华，等. 太阳能定日镜结构基于频域的风振响应分析[J]. 太阳能学报, 2009，30(6)：759-763.

GONG Bo, LI Zheng-nong, WU Hong-hua,etal. Delection analysis for reflector plate of heliostat based on thin plate flexure theory[J].Acta Energiae Solaris Sinica,2009,30(6):759-763.(In Chinese)

[16]DAVENPORT A G. Past, present and future of wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002,90(12/15): 1371-1380．

[17]BAKER C J. Wind engineering-Past, present and future[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9/11): 843-870.

[18]SOLARI G. The international association for wind engineering (IAWE): Progress and prospects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9/11): 813-842.

[19]TOMASINI G, CHELI F. Admittance function to evaluate aerodynamic loads on vehicles：Experimental data and numerical model[J]．Journal of Fluids and Structures，2013，38: 92-106.

[20]PIERRE L M S, KOPP G A, SURRY D,etal.The UWO contribution to the NIST aerodynamic database for wind loads on low buildings: Part 2. Comparison of data with wind load provisions[J]．Journal of Wind Engineering and Industrial Aerodynamics，2005, 93(1): 31-59.

[21]SOHN M H, CHANG J W. Flow visualization and aerodynamic load calculation of three types of clap-fling motions in a weis-fogh mechanism [J]．Aerospace Science and Technology, 2007, 11(2/3): 119-129.

Simulation Analysis on the Aerodynamic Characteristics and Maximum Wind Pressure Distribution of Dish Solar Concentrator

E Jia-qiang1,2†, SU Xiu-chao1, Wenming YANG2, WANG Shu-hui1,LIU Teng1, ZUO Wei1

(1. College of Mechanical and Vehicle Engineering, Hunan Univ, Changsha，Hunan 410082, China;2.Dept of Mechanical Engineering, National Univ of Singapore, 9 Engineering Drive 1, Singapore 117576)

For the problem of the optimal shelter posture of dish solar concentrator, the flow fluid model of a dish solar concentrator was established by using fluid control equations, the calculated flow velocity and pressure were then loaded into the front and back surfaces of the dish solar concentrator, and then simulation analysis of the aerodynamic characteristics and pressure distribution of dish solar concentrator was carried out. The results show that wind speed has great influence on the maximum pressure of the central area of the dish solar concentrator surface and the strength and rigidity at the center of the dish solar concentrator should be improved. Besides, the lift force, drag force, lateral force and maximum surface pressure of the dish solar concentrator increase with the increase of wind speed, especially the maximum surface pressure, while wind coefficients change little with the change of wind speed. In addition, relatively big errors exist in the calculated values of lift force coefficient, drag coefficient, lateral force coefficient and maximum surface pressure when not considering the effect of fluid-structure interaction. Moreover, the maximum surface pressure of dish solar concentrator varies intricately with change of azimuth angle, and elevation angle and it reaches to maximum when the elevation angle is 0° and the azimuth angle is 45°.

concentrator; virtual wind tunnel experiments; aerodynamic characteristics; solar energy; fluid-structure interaction

1674-2974(2015)02-0008-09

2014-01-13

国家留学基金资助项目(201208430262)；武器装备预研重点项目(9140A2011QT4801)

鄂加强(1972-)，男，湖南湘潭人，工学博士，博士生导师†通讯联系人，E-mail:ejiaqiang@126.com

TK514

A