局域共振声子晶体失谐梁的减振特性研究

张邦基,黄训浩,张 农,谢庆喜

(湖南大学 汽车车身先进设计制造国家重点实验室, 湖南 长沙 410082)

局域共振声子晶体失谐梁的减振特性研究

张邦基,黄训浩†,张 农,谢庆喜

(湖南大学 汽车车身先进设计制造国家重点实验室, 湖南 长沙 410082)

通过把声子晶体中的局域共振特性应用到梁上形成一种局域共振梁，在局域共振周期梁的基础上，引入晶格参数失谐，提出一种新型的局域共振失谐梁.对失谐梁和周期梁分别进行正弦激励响应和频率响应分析，并改进能量法，可得出结论：通过选择合适的失谐参数，可使失谐梁较传统周期梁具有更好的减振特性.

失谐梁；正弦激励响应分析；频率响应分析；能量法

随着机械工程的快速发展，人们对舒适性的要求越来越高.因此，必须注重对减振特性技术的研究，尤其是工程结构的减振特性.梁类结构作为工程中的一种基本的结构，是产生振动的主要载体，因此梁类结构成为了减振特性的主要研究对象.

通过对声子晶体的研究[1-2]，发现声子晶体具有带隙的特性[3]，落在带隙中的弹性波是禁止传播的.类比声子晶体的结构与性质，将声子晶体中的局域共振特性应用到梁上形成一种局域共振梁[4].然而由于实际工程中，振动和噪声的传递是呈现倍频成分的，单振子就不能满足工程要求，而周期排列的振子在工程中会有一定的减振的性能[5].

为了寻找更好的减振技术，本文引入晶格参数失谐[6]，也就是说通过改变相邻振子的间距，使共振单元的排列无规律，控制失谐量的大小范围，提出一种新型的局域共振声子晶体失谐梁.再对失谐梁进行正弦激励响应和频率响应的仿真并和周期梁进行响应幅值的比较，并结合能量法分别计算两者的能量，发现并确定失谐梁比周期梁具有更好的减振特性，为减振技术的研究提供了一种新的方法.

1 局域共振失谐梁减振实质

本文所提出的局域共振失谐梁实际上也是一种新型的多振子共振梁，在周期梁的基础上引入晶格失谐参数，它可以简化为弹簧-质量模型[7]，相当于一种新型的动力吸震器.多个弹簧-质量模型分布在细长梁结构上可以产生纵向振动的局域共振带隙，禁止弹性波的能量的传播，如图1所示.它和传统动力吸振器减振技术相比，局域共振失谐梁减振实质：它是利用多振子共振梁结构的带隙特性来抑制结构中的弹性波传播，来达到减振的目的.

图1 局域共振失谐梁简化结构

假设梁仅作对称弯曲振动,取梁的轴线水平方向作为x轴，并且振动过程中梁仅有y方向横向位移u(x,t).同样假设局域共振单元的间距远大于截面尺寸，满足欧拉—伯努利梁条件.则单个周期内沿x轴传播的弯曲弹性波方程满足如下波动方程[8]：

(1)

式中w(x,t)为横向振动位移；ρ为密度；E为弹性模量；A为梁的截面积；I为抗弯截面系数.

(2)

基于能量法从相对能量率的角度来计算弹性波在传播过程中的能量.能量与幅值的平方是成正比的，即E∝A2，定义时域的能量为：

(3)

式中kt为比例系数；A(t)为拾取点t时刻的幅值；t0为采样时间.

由于失谐梁与周期梁同一位置的A(t)不同，弹性波在共振梁传播过程中的能量也会产生差异.

因此，通过合理地调整晶格失谐参数，便可实现失谐梁比周期梁具有更好的减振特性.

2 局域共振失谐梁模型的建立

2.1 周期梁模型

本文选用的周期梁模型如图2所示，梁的总长设计为600mm，共有6个局域共振单元，其中每一个共振单元的长度为25mm，相邻两个共振单元之间的间隔为75mm.梁的材料是树脂[9]，密度1 180kg/m3,杨氏模量0.435×1010Pa，泊松比0.367 9；中间层的材料为硫化橡胶，密度1 300kg/m3,杨氏模量1×106Pa，泊松比0.470 6；最外层的材料为铅，密度11 600kg/m3,杨氏模量4.08×10-10Pa，泊松比0.369 1.梁的半径为5mm，中间层的橡胶外径为8mm，最外层的铅外径为10mm.

图2 周期梁及其截面图

2.2 失谐梁模型

本文在周期梁的基础上直接引入20%的晶格参数失谐，提出一种全新的局域共振梁，如图3所示.晶格参数失谐的程度用失谐量来表示.选用的材料参数以及梁和局域共振单元的几何参数与周期梁完全相同，与周期梁的区别是：局域共振单元不再周期排列，相对于周期梁的共振单元有轴向平移.

图3 失谐梁和周期梁共振单元间距图

Δ=-(a+l)×β～(a+l)×β

(4)

式中a为周期梁两个局域共振单元间的距离，a=75mm；l为共振单元的长度，l=25mm；β为失谐百分比，β=20%；Δ为允许的失谐范围.

通过式(4)计算可知失谐范围为-20mm～20mm.

此处失谐梁共振单元的失谐量分别取为 -5mm,15mm,10mm,5mm，-15mm，-10mm.

取轴的最左端的坐标为0，失谐梁和周期梁的共振单元的位置坐标如表1所示.di表示失谐梁和周期梁第i个共振单元的间距，如图3所示.d1=5 mm，d2=10 mm，d3= 20 mm，d4=25 mm，d5=10 mm，d6=0 mm.

表1 失谐梁和周期梁的共振单元的位置坐标

3 基于能量法的减振特性分析

3.1 正弦激励响应分析

建立周期梁和失谐梁的有限元模型.设置接触条件，材料参数以及属性，对梁的一端进行固定.在梁的自由端施加垂直于梁的轴线方向的正弦激励x(t)=sin (250 πt)mm，激励时间为一个信号周期0.008s.分别在距离失谐梁和周期梁的固定端轴向距离5mm处拾取响应，采样时间为0.04s.失谐梁的激励点和拾取点如图4所示,周期梁的激励点和拾取点在相同位置.仿真分析后将失谐梁和周期梁的响应曲线放在一起进行比较，得到的正弦激励响应曲线如图5所示.

图4 失谐梁响应激励点和拾取点

时间/s

通过对比失谐梁和周期梁的响应曲线可知，失谐梁响应在采样时间内振动响应幅值的绝对值要明显小于周期梁，即失谐梁能更好地抑制弹性波的传播.

为了更可靠地验证失谐梁的减振特性效果确实要优于周期梁，基于能量法从相对能量率的角度来验证.

根据式(3)，失谐梁比周期梁少传播弹性波的相对能量率η可由下式计算：

(5)

式中EΔ为失谐梁中弹性波传播过程的总能量；ET为周期梁中弹性波传播过程的总能量；A(t)Δ为失谐梁拾取点t时刻的幅值；A(t)T为周期梁拾取点t时刻的幅值.

经过计算得相对能量率η=-32.87%.施加正弦激励后产生的弹性波经过失谐梁传播的能量要比周期梁下降32.87%，能量减少比较明显.因此，失谐梁在抑制弹性波传播时效果要比周期梁好.

3.2 频率响应分析

有限元模型进行同正弦激励响应分析一样的前处理，对梁的一端进行固定.在梁的另一端，也就是自由端，施加大小为1 000N的力，方向与杆的轴向垂直，频率变化范围为0～300Hz的信号激励，分别在距离失谐梁和周期梁的固定端轴向距离5mm处拾取响应，仿真分析后将失谐梁和周期梁的响应曲线放在一起比较，得到的瞬态响应曲线，如图6所示.

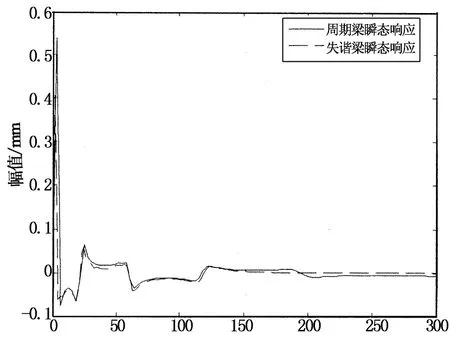
频率/Hz

通过对比失谐梁和周期梁的频率响应曲线可知，失谐梁的频响在0～20Hz的频率范围内幅值的绝对值明显要比周期梁小很多，在图中其它频率区间失谐梁较周期梁的振动幅值的绝对值只是略小并不太显著，可以通过两者的频率响应函数dB的曲线来进行对比，如图7所示.共振峰频率是由局域共振结构的固有模态所决定的.我们可以发现在60～110Hz范围内，失谐梁相对于周期梁的分贝值差别不大.在0～60Hz以及大于110Hz的高频范围内，减振特性效果非常显著，而且频率越高作用越大.

频率/Hz

类比时域，基于能量法计算频域内失谐梁比周期梁少传播弹性波的相对能量率的大小.

定义频域的能量为

(6)

式中kf为比例系数；Δf为频率的变化范围;A(f)为拾取点在激励频率为f时的幅值.

(7)

式中f0为激励截止频率，f0=300Hz；A(f)Δ为失谐梁的拾取点在激励频率为f时幅值；A(f)T为周期梁的拾取点在激励频率为f时幅值；η为失谐梁比周期梁少传播弹性波的相对能量率.

由式(6)和(7)计算得相对能量率η=-35.35%.施加激励后产生的弹性波经过失谐梁传播的能量要比周期梁下降35.35%，能量大大减少.所以，失谐梁在抑制弹性波传播中时效果要比周期梁好.

4 结 论

经过基于能量法的减振特性分析，无论是正弦激励响应分析还是频率响应分析，通过分别对比周期梁和失谐梁的幅值和能量，可以发现：

1)在一定的失谐参数下，弹性波在该失谐梁中传播的幅值的绝对值要明显小于周期梁，所以该失谐梁在抑制弹性波传播的幅值时效果要比周期梁好.

2)失谐梁在0～60Hz以及大于110Hz的高频范围内，减振效果非常显著，而且频率越高作用越大.

3)当失谐梁有20%的晶格参数失谐时，正弦激励响应时弹性波的相对能量率为-32.87%；频率响应时弹性波的相对能量率为-35.35%.弹性波在该失谐梁中传播时的能量要大大减小.因此该失谐梁在抑制弹性波传播能量时效果要比周期梁好.

因此，可以得出结论：通过选择合适的失谐参数，可使失谐梁较周期梁具有更好的减振特性.

[1]KUSHWAHAMS,HALEVIP,DOBRZYNSKIL,etal. Acoustic band structure of periodic elastic composites [J]. Physical Review Letters, 1993, 71(13): 2022-2025.

[2] MARTINEZ-SALA R, SANCHO J, SANCHEZ J V,etal. Sound attenuation by sculpture [J].Nature ,1995, 378(16): 241.

[3] 肖勇.局域共振型结构的带隙调控与减振降噪特性研究[D].长沙: 国防科技大学研究生院，2012.

XIAO Yong. Research on control and damping characteristics of the locally resonant band gap structure[D]. Changsha: National University of Defense Technology Graduate School, 2012.(In Chinese)

[4] 黄小益，彭景翠，张高明，等.声子晶体中声子频率带隙与散射截面的关系[J]. 湖南大学学报:自然科学版，2006，33(3):89-92.

HUANG Xiao-yi, PENG Jing-cui, ZHANG Gao-ming,etal. Relation between the gap and scattering cross section of the phonon frequency band in phononic crystal [J]. Journal of Hunan University:Natural Sciences, 2006,33(3)：89-92. (In Chinese)

[5] LIU Y Z, SHAO L H, WANG G,etal. A heuristic model for estimating the lowest gap of locally resonant phononic crystals [C]//ASME, Noise Control and Acoustics Division, NCA． 2005：149-153．

[6] 王刚，温激鸿，温熙森.细直梁弯曲振动中的局域共振带隙[J].机械工程学报，2005，41(10):107-110.

WANG Gang,WEN Ji-hong,WEN Xi-sen. Local resonance band gap of flexural vibration of beam[J]. Journal of Mechanical Engineering，2005，41(10):107-110. (In Chinese)

[7] WANG Gang, WEN Xi-sen, WEN Ji-hong,etal. Quasi one-dimensional periodic structure with locally resonant band gap[J]. ASME Journal of Applied Mechanics,2006,73(1): 167-169.

[8] 文岐华,左曙光，魏欢，等.多振子梁弯曲振动中的局域共振带隙[J].物理学报，2012,61(3)：034301.

WEN Qi-hua, ZUO Shu-guang,WEI Huan,etal. Locally resonant elastic wave band gaps inflexural vibration of multi-oscillators beam[J]. Journal of Physics,2012,61(3)：034301. (In Chinese)

[9] 舒海生,张法，余豪华，等.一类局域共振型声子晶体梁的带隙分析[J].哈尔滨工程大学学报，2011,32(9):1249-1253.

SHU Hai-sheng,ZHANG Fa, YU Hao-hua,etal. Band gap analysis of a class of locally resonant phononic crystal beam[J]. Journal of Harbin Engineering University, 2011,32(9):1249-1253. (In Chinese)

Research on Properties of Vibration Attenuation in Phononic Crystal Detuning Beam with Local Resonant Structure

ZHANG Bang-ji，HUANG Xun-hao†，ZHANG Nong，XIE Qing-xi

(State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan Univ, Changsha，Hunan 410082，China)

The characteristic of phononic crystals local resonance was applied to beam to form a local resonat beam. Based on local resonant beam, and by introducing analogy lattice parameter mismatch, a local resonance model of detuning beam was obtained. Through sine excitation response analysis and frequency response analysis of local resonance periodic beam and detuning beam respectively, and combined with the improved energy method, it can be concluded that, by choosing the appropriate detuning parameters，detuning beam is better than periodic beam in the characteristics of vibration reduction．

detuning beam; sine excitation response analysis; frequency response analysis; energy method

1674-2974(2015)02-0055-05

2013-11-22

国家自然科学基金联合基金资助项目(U1234208); 西南交通大学牵引动力国家重点实验室开发课题资助(TPL1310)

张邦基(1967-)，男，湖南长沙人，湖南大学副教授，博士†通讯联系人，E-mail:huangxunhao123@126.com.

TH113.1

A