基于Gröbner基的图动态染色求解方案

何文峰，张勇军，符一平

( 海南大学 信息科学技术学院，海南 海口 570228)



基于Gröbner基的图动态染色求解方案

何文峰，张勇军，符一平

( 海南大学 信息科学技术学院，海南 海口 570228)

摘要：考察了一般有限连通图的动态染色方案以及动态色数，首先利用多元多项式方程组对其进行建模，然后利用方程组对应的Gröbner基来判定方程组解存在性，进而达到判定图的动态染色方案的存在性的目的，最后给出求动态色数及相应动态染色方案的方法，并给予实例验证.

关键词：动态染色； 动态色数； Gröbner基

图染色问题就是用最少种类的颜色对图的点、边、面以某种规则进行染色，研究染色所用色数以及设计对应的染色方案就成为图染色的基本工作.近年来，随着通信以及计算机技术方面的长足发展，对染色问题提出了更高的要求.在此背景之下，2001年Montgomery在文献[1]中提出动态染色概念，同时证明了一般图的动态色数上界为Δ+3.林越等在文献[2]中得到平面图的动态色数上界为5的结论，除此之外，还有一些学者对特殊图的动态色数给予了研究，如文献[1],[3-9]分别对多重完全图、二部完全图、完全图、树、k-正则图、伪哈林图、单圈图及双圈图等特殊图的动态色数进行了研究.

从以上研究的过程中可以发现，几类特殊图和平面图的动态染色的上界已经研究的较清楚,但一般图的动态色数还知之甚少.因此，笔者考察了一般有限连通图的动态染色方案以及动态色数，首先对其进行多元多项式方程组建模，然后利用方程组对应的Gröbner基来判定方程组解的存在性，进而达到判定图的动态染色方案的存在性的目的，最后给出求动态色数的可行方法.

1预备知识

本文提到的图G(V，E)均指n阶连通图，V(G)表示G(V,E)的顶点集，E(G)表示G(V,E)的边集，

N(v)表示G(V,E)中顶点v的邻点集，dG(v)=d(v)=|N(v)|表示G(V,E)的顶点v的度.

定义1 图G(V,E)的动态d-染色是一个这样的映射C:V(G)→C(d)={1,2,…，d},且满足：

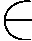
定义2若图G(V,E)存在动态d-染色，而不存在动态(d-1)-染色，那么就把d称为图G(E,V)的动态色数，记为χd(G).

定义3 设图G(V,E)是一个有限的简单连通图，邻接矩阵(AdjacencyMatrix)记为A=(aij)n×n，其中，

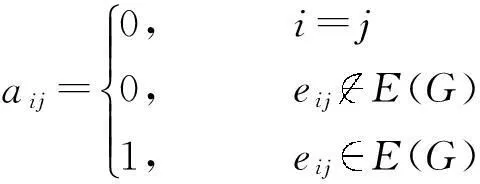
2描述动态k-染色的多元多项式方程组的建立

图G(V,E)动态d-染色就是用颜色集{1,2,…,d}对G(V,E)进行正常顶点染色(即相邻顶点染不同色)，同时，若某顶点有2个以上邻点，要使得至少有2个邻点染不同色.如果要把图G(V,E)动态d-染色用多元多项式方程组描述出来，即根据图G(V,E)的动态d-染色的定义建立多元多项式方程组模型.现取顶点染色方案向量X=(x1,x2,…，xn)T，其中，

若顶点vi用颜色集{1,2,…，d}中的颜色染色，那么vi的颜色xi为多项式方程

(xi-1)(xi-2)…(xi-d)=0

的解.

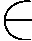
(|xi-xj|-1)(|xi-xj|-2)…(|xi-xj|-(d-1))=0

的解，而方程

(|xi-xj|-1)(|xi-xj|-2)…(|xi-xj|-(d-1))=0

等价于

((xi-xj)2-1)((xi-xj)2-22)…((xi-xj)2-(d-1)2)=0.

对于图G(V,E)任一顶点vi，其度(即邻边数目)dG(vi)=AiAiT， 通过邻接矩阵A 就可以确定. 若dG(vi)=AiAiT=1，正常顶点染色方案一定符合|C(N(vi))|≥min{2,dG(vi)}；若dG(vi)=AiAiT≥2,由邻接矩阵A一定可以找到vi的邻点集N(vi)={vi1,vi2,…,vidG(vi)}，若要求N(vi)={vi1,vi2,…,vidG(vi)}至少染2种颜色(即要求|C(N(vi))|≥min{2,dG(vi)}),那么顶点vi1,vi2,…,vidG(vi)对应的颜色xi1,xi2,…,xidG(vi)就是方程

的解.

由以上过程，可以看到G(V,E)的动态染d-色方案与方程组

的解有关.用定理1给定关系.

定理1 方程组Sd的每个解对应图G(V,E)的一个动态d-染色方案，且是一一对应.

证明充分性方程组Sd的解X会使第一组方程和第二组方程都成立，那么X就会使得每个顶点都在颜色集{1,2,…，d}中选一种颜色，且相邻的点颜色不同；方程组Sd的解X会使第三组方程成立，那么X就会使得任何有2个邻点以上的顶点有至少2个邻点染色不同.因此，方程组得解X就是图G(V,E)的一个动态d-染色方案.

必要性若X是图G(V,E)的一个动态d-染色方案，X就是图G(V,E)的一个顶点正常染色方案，必然符合第一组方程和第二组方程，即代入必使其成立.X要使得任何有2个邻点以上的顶点有至少2个邻点染色不同，那么代入第三组方程，第三组方程也成立.由此，X代入方程组Sd会使得其成立，即X是方程组Sd的一个解.

综上所述，方程组Sd的每个解对应图G(V，E)的一个动态d-染色方案.且是一一对应.

3图G(V,E)的动态d-染色方案存在性的Gröbner基判别方法

对于图G(V,E)，动态d-染色方案是否一定存在？存在的话，是否d种颜色构成的任一方案都可以对图G(V,E)进行动态染色？这些问题的解决可以从定理1中找到线索，方程组Sd的每个解对应图G(V,E)的一个动态d-染色方案，且是一一对应.因此，要判定图G(V,E)是否动态d-染色，是否d种颜色构成的任一方案都可以对图G(V,E)进行动态染色就可以转化为多元多次方程组解的存在性问题及求解问题.对于多元多项式方程组根的存在性可以借助于Gröbner基来判定.因此，定理2就可以解决所提问题.

定理2对于给定的d(其中0

1)图G(V，E)是动态d-染色的⟺Sd有解；

2)倘若Sd有解，那么Sd的所有解就给出图G(V,E)的所有的动态d-染色方案；

3) Sd有解⟺理想I的Gröbner基不包括非零的常数，其中，理想I是Sd各方程左端多元多项式在环R=C[x1,x2,…,xn]中生成的.

证明 1)和2)由定理1(方程组Sd的每个解对应图G(V,E)的一个动态d-染色方案，且是一一对应)可以直接推得成立.

由于Sd解的存在性⟺I的Gröbner基生成的多元多项式方程组解的存在性，如果Sd有解，那么V(I)≠Ø，即理想I的Gröbner基不包括非零的常数；若理想I的Gröbner基不包括非零的常数，那么I的Gröbner基生成的多元多项式方程组解就存在，即方程组Sd有解.3)成立.

4动态色数χd(G)的确定

定理3Sd-1无解而Sd有解⟺χd(G)=d.

证明充分性根据定理2 1)的逆否命题可知，如果Sd-1无解，那么图G(V，E)就不存在动态(d-1) -染色，根据定理2 1)可知，如果Sd有解，那么图G(V,E)就存在动态d-染色，由动态色数的定义可知χd(G)=d.

必要性如果χd(G)=d，根据动态色数的定义就知若要对图G(V,E)进行动态染色，最少需要d种颜色，即动态d-染色存在，而动态(d-1) -染色不存在，结合定理2 1)和2)就可以得到Sd-1无解而Sd有解.

5实例验证

根据定理1、定理2和定理3，在实例中可以依照方程组S2,S3,S4…逐个利用数学软件Maple计算所对应的理想I的Gröbner基,通过观察理想I的Gröbner基是否包含不为零的常数的方法来确定所对应的染色方案是否存在，若存在，就利用理想I的Gröbner基生成的多元多项式的方程组取得图G(V,E)的所有的动态d-染色方案，同时根据定理3确定χd(G).

例有限图G(V,E) (如图1),其中V={v1,v2,v3,v4,v5,v6}，邻接矩阵为

根据定理3，先验证G(V,E)的动态2-染色的存在性，再验证G(V,E)的动态3-染色的存在性，依次进行下去，直到找到合适的d值,同时得到相应的动态染色方案.

动态2-染色

利用Maple中计算Gröbner基的程序可以计算出G2={1}是IS2的唯一约化Gröbner基，由定理2可得S2无解，即图G(V,E)的动态2-染色不存在.

动态染色

利用Maple中计算Gröbner基的程序可以计算出

G3={x63-6x62+11x6-6,x62+x52+x5x6-6x5-6x6+11,x5+x6+x4-6,x5x6-x3x6-x3x5+x32,

x6+x5+x1-1,x3+x2-x6-x5,x5+x1-6}.

由定理2说明S3有解，且与G3对应的方程组G3=0的解相同，在软件Mapple中调用程序解G3=0，

得到结果(3,2,1,3,2,1)，(3,1,2,3,1,2)，(3,1,2,3,2,1)，(3,1,2,3,2,1)，(3,3,1,3,1,2)，(2,3,1,2,1,3)，(1,3,2,3,1,2)，(2,1,3,2,3,1)，(1,2,3,1,2,3)，(1,3,2,1,3,2)，(1,2,3,1,3,2)，(2,1,3,2,1,3).

由定理2也说明这些解恰好是动态3-染色的所有方案，同时，由定理3也可以知道χd(x)=3.

参考文献：

[1] Montgomery B.Dynamic coloring[D].West Virginia:West Virginia University, 2001.

[2] 林越,赵克文.平面图的动态着色[J].郑州大学学报(理学版),2010,42(3):34-35.

[3] Alishahi M.On the dynamic coloring of graphs[J].Discrete Applied Mathematics,2011,159(3):152-156.

[4] Esperet L.Dynamic list coloring of bipartite graphs [J].Discrete Applied Mathematics,2010,158(17):1 963-1 965.

[5] 秦健,张岩.单圈图和双圈图的动态色数[J].山东大学学报(理学版),2007,42(10):37-40.

[6] Akbari S,Ghanbari M,Jahanbekam S.On the list dynamic coloring of graphs[J].Discrete Applied Mathematics, 2009,157(14):3 005-3 007.

[7] Meng X Y,Miao L Y,Su B T.The dynamic coloring numbers of Pseudo-Halin graphs [J].Ars Combinatoria, 2006, 79:3-9.

[8] Kim S J,Park W J.List Dynamic coloring of sparse graphs[J].Combinatorial Optimization and Applications,2011,6 831:156-162.

[9] Kim S J,Lee S J,Park W J.Dynamic coloring and list dynamic coloring of planar graphs[J].Discrete Applied Mathematics,2013,161:2 207-2 212.

[10] 王桂平,王衍,任嘉辰.图论算法理论、实现及应用[M].北京：北京大学出版社,2011.

Dynamic Coloring Solving Scheme Based on Gröbner Basis

He Wenfeng, Zhang Yongjun, Fu Yiping

(College of Information Science and Technology, Hainan University, Haikou 570228，China)

Abstract：In the report, the dynamic coloring solution of the Limited connected graph and the dynamic coloring number were investigated. Firstly, the multivariate polynomial equation group was used to construct a model of the dynamic coloring problem; Secondly, the corresponding Gröbner basis of the multivariate polynomial equations was used to determine the existence of solutions, which can judge the existence of the dynamic coloring protocol; Lastly, the dynamic coloring number and the solution method of the corresponding dynamic coloring were proposed, and which was validated by specific examples.

Keywords：dynamic coloring; dynamic coloring number; Gröbner basis

中图分类号：O 157.5

文献标志码：ADOl：10.15886/j.cnki.hdxbzkb.2015.0023

文章编号：1004-1729(2015)02-0125-05

收稿日期：------------------------ 2014-10-10

作者简介：何文峰(1978-)男，陕西蒲城人，讲师.通信作者： 张勇军(1977-)男，陕西渭南人，讲师.