泥石流块石冲击下新型钢管混凝土桩林坝“品”单元动力响应分析

王秀丽，关彬林，李俊杰

(1.兰州理工大学土木工程学院，甘肃兰州 730050;2.西部土木工程防灾减灾教育部工程研究中心，甘肃兰州 730050)

0 引言

泥石流是发生在山区的一种重力地貌现象，是泥沙石块等松散固体物质和水，以及少量空气的混合体在重力作用下沿着沟床或坡面向下运动的特殊流体。泥石流具有暴发突然、流速快、历时短暂、危害严重等特征。我国每年由于泥石流灾害死亡人数都位于全国水旱灾害死亡人数的前列，经济损失从数百万元到数亿元［1］。

我国对泥石流灾害的治理始于20世纪50年代，经过近60年的研究与实践，已由局部的单一工程措施发展到工程防御、生物防御、预测与报警、环境保护与行政管理相结合的综合防治体系［1］，总结出“以防为主，防治结合，因地制宜，因害设防，突出重点，综合治理”的灾害防治原则，形成了“预防与治理相结合，工程措施与生物措施相结合，灾害治理与资源利用相结合”的成套减灾技术［2］。治理泥石流最有效和最快捷的措施是修建各种拦挡坝，它有泄洪、拦渣、固床、稳坡、控制固体物质补给量、防止沟道下切及沟壑继续发展的功效。在泥石流灾害防治中，通常采用多道坝分级拦挡，在泥石流沟中上游修建透水型坝体，拦截大块石，下游修建实体重力坝，拦截水与泥沙。透水型拦挡坝适用于流体中固相物质级配宽，大漂砾含量高的稀性泥石流和水石流，也可用于密度较低的碎屑流;高密度粘性泥石流和泥流则当慎用［3］。巨石在沟中上游如不进行拦截，从上面滚落下来携带巨大的能量，对下游的各种结构将造成巨大的破坏，甚至人员伤亡。现有拦截大块石的常用结构就是钢筋混凝土桩林，它具有拦挡效果好，刚度大，抗冲击能力强，耐久性好的优点，不过它也有配筋过密导致施工困难，桩之间协同能力不强，受块石撞击部位易破碎，造价高的缺点。鉴于钢管混凝土具有承载力高、塑性和韧性好，经济效益显著和施工快捷的优点［4］，以及王蕊、李珠［5-6］等人做了一系列试验研究了钢管混凝土构件抗侧向冲击性能，发现钢管混凝土构件在冲击下具有很好的塑性变形能力与耐撞性，遂提出一种新型拦挡坝—钢管混凝土桩林(图1)。当泥石流中大块石撞击坝体的同时，肯定还有小块石与泥浆作用于坝体上，出于安全与设计角度考虑，因此取其中一典型“品”字形三桩结构利用国际通用计算动力荷载的非线性有限元软件ANSYS/LS-DYNA进行建模分析并研究其在大块石撞击下的动力响应，以便为钢管混凝土桩林这种结构的工程设计与应用提供参考。

图1 钢管混凝土桩林平面图Fig．1 The plan of concrete-filled steel tubular piles

1 冲击作用分析

1.1 巨石冲击脉冲形式

钢管混凝土桩林是种新型坝，现有的泥石流灾害防治工程设计规范未对其设计做说明。本文中关于桩间距的确定参考规范［7］中的钢筋混凝土桩林的设计要求，b/Dm=1.5～2(b为桩之间的净间距，Dm为泥石流最大粒径)，坝体的竖向格栅孔高度尺寸选择参考甘肃省舟曲县三眼峪沟泥石流灾害治理工程的施工图设计，由施工图可知底部孔的高度比上部孔的高度要小，且基本满足b/h1=1.5～2(b同前，h1为底部矩形孔的净高度)，b/h2=1～1.5(b同前，h2为除底部孔外的上部矩形孔的净高度)。本文中桩的直径取为114 mm，Dm取为300 mm。

冲击荷载是指外部荷载瞬时地将动量施加到结构上的随时间迅速变化的荷载，是一种短时作用。国内学者吴积善等根据实测的泥石流冲击力过程曲线对泥石流冲击荷载进行了研究，将泥石流冲击荷载概化为锯齿形脉冲、矩形脉冲和尖峰型脉冲三类［8］。钢管混凝土桩林主要对泥石流中大块石进行拦挡，以受大块石的冲击作用为主，属尖峰型脉冲(图2)。

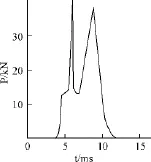
图2 尖峰型脉冲荷载Fig．2 Peak pulse load

该类波形反映泥石流冲击作用时间短，全过程仅几毫秒到十几毫秒，认为是泥石流体中粒径较大的固相颗粒或块石动力作用的结果，能更精确的反应钢管混凝土桩林受泥石流大块石的冲击。

1.2 巨石冲击力计算方法

泥石流对钢管混凝土桩林的冲击力包括泥石流整体冲击力和泥石流中大块石的冲击力［7］，由于钢管混凝土桩林受力面积小，作用于坝体的泥石流整体冲击力将很小，主要以大块石的冲击力为主。

式中:Fb为泥石流巨石冲击力/kN;E为工程构件弹性模量/kPa;J为工程构件截面中心轴的惯性矩/m4;L为构件长度/m;V为石块运动速度/(m/s);W为石块重量/kN;g为重力加速度(取g=9.8 m/s2);α为块石运动方向与构件受力面的夹角/(°)。

1.3 球体模拟巨石冲击

本文采用刚球模拟泥石流冲击过程中的块石，在有限元软件ANSYS/LS-DYNA中建立球体几何模型，球体单元选取软件中特有的的三维实体单元SOLID164，采用Rigid模型，密度与泊松比取自花岗岩，密度为2800 kg/m3，弹性模量为50 GPa，泊松比为0.29。冲击体由于是刚体材料，在划分网格时，可以尽量划分的精细来提高运算的精度，并不影响运算的速度。直径300 mm球体在网格划分时，先将球体切割成等大小的8块，再进行映射划分，网格大小为20 mm，其有限元模型如图3。

图3 球体有限元模型Fig．3 The finite element model of sphere

2 钢管混凝土桩林“品”字形结构单元建模

2.1 单元类型

钢管混凝土桩林“品”字形结构有限元模型中，混凝土与钢管均采用具有较高精度和较好收敛性的8节点六面体实体单元SOLID164。

2.2 材料特性

钢管对内填混凝土形成套箍作用，使其三向受压，从而使它具有更高的抗压强度和压缩变形能力。因此桩管内混凝土选塑性各向同性强化模型Bilinear Isotropic Model［9］，本文中模拟要用到 C30，C40，C50 和C60等级混凝土，性能参数取值参考规范［10］见表1，切线模量均为3.5 GPa。

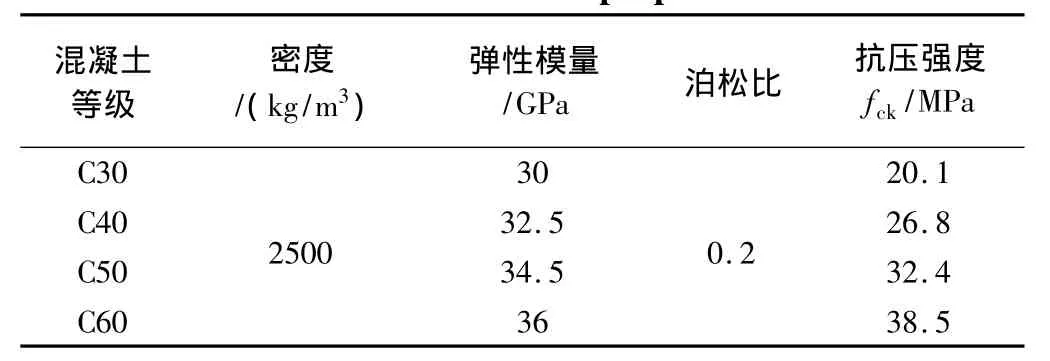
表1 混凝土特性Table 1 Concrete properties

在快速加载条件下，许多金属材料的屈服极限有明显的提高，而屈服的出现有滞后现象。因此钢管选用塑性随动强化材料模型Plastic Kinematic Model，其包括等向强化、随动强化以及两者的结合模型，其依赖于应变率及失效应变。应变率通过Cowper-symonds模型得以实现，该模型能够依赖于应变率的参数来确定屈服应力，其值为:

式中:σ0为静态屈服应力;为应变率;C和P为应变率参数为有效塑性应变;Ep是由Ep=EtEs/(Es-Et)给出的塑性硬化模量。

本文中模拟要用到不同厚度的钢管Q235，屈服强度σ0均为235 MPa，弹性模量Es均为206 GPa，切线模量Et均为0.65 GPa，泊松比ν均为0.3，密度均为7850 kg/m3，取0.2。钢管为普通热轧钢，硬化参数β 取0.2，C取 50.1，P取 4.0［10］。显式动力分析中为阻止结构的非真实振荡，需要定义阻尼。本模型中考虑材料阻尼，钢材料阻尼系数取0.005，混凝土材料阻尼系数取0.04。

2.3 网格划分

本文选取钢管混凝土桩林坝的“品”字形三桩结构进行动力响应分析，模型由三根钢管混凝土桩与桩之间的双层连梁组成。每根桩截面均相同，高度为0.8 m，桩心间的距离为0.6 m，每两根桩在0.3 m高度与0.75 m高度处分别设置一根钢管梁，钢管梁的截面尺寸均相同。模型分析中桩钢管外直径均为114 mm，壁厚分别为3.5 mm、3.8 mm、4.2 mm、4.5 mm 四种厚度，钢管梁外直径为51 mm，壁厚为3.5 mm。受冲击的桩称为前桩，其余两桩称为后桩。由于块石撞击三桩结构位置具有不确定性，文中取前桩管与梁管节点处750 mm高度(位置定义为I)与两道梁管中间500高度处(位置定义为Ⅱ)这两个典型位置进行冲击分析，为了减少运算机时和方便模型的建立，冲击球距冲击部位的距离在任何计算工况下均取10 mm。三桩结构在网格划分之前应先对桩管与梁管进行divide，再对钢管桩底面进行面划分，前桩沿外环周取32份，后桩沿外环周取24份，桩管里面的混凝土沿着桩高度方向Sweep，前桩取40份，后桩取25份。冲击部位处进行SOLID164自由划分，网格大小取10 mm，其余梁管桩管节点处自由划分，网格大小取15 mm。冲击部位自由划分以保证沙漏能占总能量的比例不超过10%，且滑移能不出现负值。钢管混凝土桩林的“品”字型三桩结构网格划分如图4。

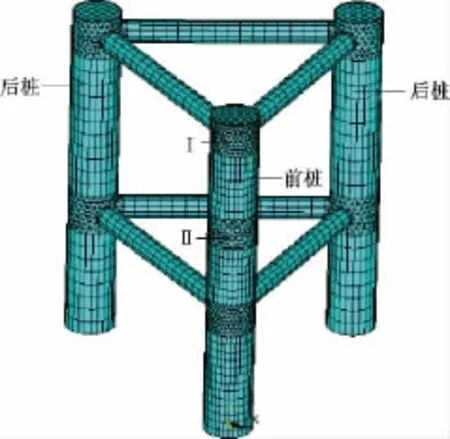
图4 三桩结构有限元网格划分Fig．4 Grid division of the three-pile structure

2.4 接触定义

冲击荷载通过冲击球与钢管的接触面来施加，本模型中采用面面自动接触类型，并假定接触面无摩擦，接触算法采用对称的罚函数法。在钢管壁与混凝土单元的粘结模拟方面，大多数研究者(Neogi，Tomii，Shakirkhalil等)均假定钢管与混凝土完全黏结，少数研究者在钢管单元与混凝土单元之间加入了滑移单元或间隙单元，结果表明考虑界面之间的滑移性能对钢管混凝土结构整体性能影响不大。因此本文中钢管与混凝土采用完全黏结处理。

2.5 边界条件

钢管混凝土桩林的“品”字形三桩结构柱脚采用埋入式刚接柱脚，故本模型中桩根部可视为固端，通过对桩根部外圈钢管节点x，y，z方向位移约束，对核心混凝土采用只约束其z方向来模拟固端。

3 计算结果及分析

钢管混凝土桩林结构在侧向冲击荷载作用下，会产生材料的相互作用、弹塑性变形、动态损伤等多种效应耦合，其撞击破坏是个非常复杂的非线性动力过程，它与钢、混凝土材料特性、几何参数，撞击物形状、质量、速度、冲击部位、结构约束等情况密切相关。

3.1 冲击力的时程曲线与变形分析

泥石流浆体的动压力及其所含块石的撞击力是危害防治工程构筑物的直接因素，而后者往往是导致结构破坏的最主要荷载，因此冲击力是拦挡坝抗冲击性能的一个重要评价指标。泥石流属于低速流，撞击拦挡坝的大块石的速度通常在10 m/s左右。为反映三桩结构(桩管为厚3.5，桩管内混凝土为C40)在不同冲击能量下的冲击力变化特性，文中给直径300 mm的球分别设速度5 m/s、7.5 m/s、10 m/s、12.5 m/s、15 m/s。为方便冲击力时程曲线的对比，将接触前的一段时间去掉，使不同速度下的冲击力时程曲线有相同的起点。图5为三桩结构Ⅰ处受不同速度球撞击的冲击力时程曲线，图6为结构Ⅱ处受不同速度球撞击的冲击力时程曲线。

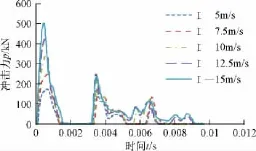
图5 Ⅰ处不同速度下的冲击力时程曲线Fig．5 Impact force vs．time curves for different velocity(Ⅰ)

图6 Ⅱ处不同速度下的冲击力时程曲线Fig．6 Impact load vs．time curves for different velocity(Ⅱ)

从图5、图6均可看出球一接触结构，冲击力在短时间内迅速达到峰值，随后下降，呈一尖峰形状，过后如能量较大时再次出现小的尖峰。究其原因，球携带巨大的能量作用在结构上，使冲击部位的附近质点在短时间内受到波及，并产生加速运动，并有局部变形产生，但结构整体还来不及发生变形，冲击力因此很快达到峰值，当结构整体变形开始发生时，冲击力开始步入下降段。Ⅰ位置冲击力直接降到0，此时刚球的速度还是保持正向，并与冲击部位一起等速运动，经过约2 ms后，结构通过变形耗能把自身的速度降了下来，结果刚球与结构再次发生了碰撞，但此时刚球速度并不是开始的那么大，引起的峰值相对最初的来说较小。Ⅱ位置冲击力下降到200 kN左右再次上升，原因在于Ⅱ位置上下端约束较强，使得它的速度比整体降的快，故冲击力再次上升，并到一峰值后下降到0，此时刚球的速度已经反向，但值较小，当结构释放部分变形能时，结构反向运动，可能赶上刚球，发生再次碰撞。从图5、图6可看出结构相同的位置受等质量的球撞击，冲击力峰值随着冲击速度的增大而增大，增幅在45.7% ～18.2%;相同速度下，Ⅱ位置比Ⅰ位置的冲击力峰值大，约为I位置的1.12倍，原因在于Ⅱ位置比Ⅰ位置能量扩散慢，Ⅱ位置离前桩固端距离比Ⅰ位置近，前桩顶面混凝土在受到撞击时能够向外变形，总的来说，Ⅱ位置比Ⅰ位置在相同的冲击速度下难于变形。

图7为三桩结构(桩管厚3.5，桩管内混凝土为C40)的Ⅰ和Ⅱ位置背部残余变形随不同速度的变化关系。从图7可看出冲击部位的残余变形随着冲击速度的增大而增大，且残余变形与速度近似于二次关系，又冲击能量与速度成二次关系，则在相同冲击球质量下，残余变形与冲击能量近似于线性关系。

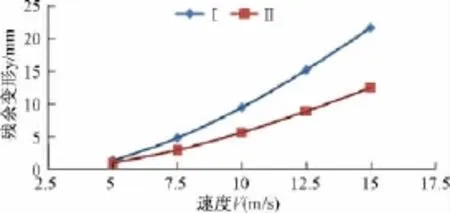
图7 不同冲击速度下的残余变形Fig．7 The residual deformation under different impact velocity

3.2 冲击力峰值参数分析

以下从不同的混凝土等级、不同的桩管套箍系数和不同的桩心距等方面对冲击力峰值的影响进行分析。

图8是三桩结构(桩管厚3.5)的Ⅰ和Ⅱ处在桩管内混凝土分别为C30，C40，C50，C60受10 m/s球撞击的冲击力峰值变化关系图。

图9是三桩结构(梁管厚3.5，桩管混凝土为C40)Ⅰ和Ⅱ位置在改变桩管厚度，不改变柱管直径情况下受10 m/s球撞击的冲击力峰值变化图。桩截面套箍系数 ξ=Asfy/Acfck，桩管 114 ×3.5、114 ×3.8、114×4.2、114 ×4.5 套箍系数分别为 1.185、1.297、1.450、1.568。

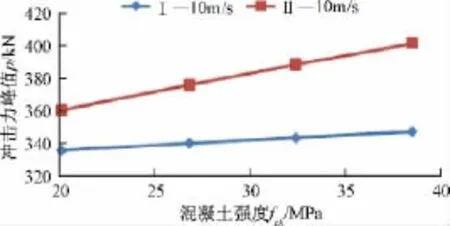
图8 冲击力峰值随混凝土强度变化关系图Fig．8 The concern curve of peak impact force and the concrete strength

图9 冲击力峰值随套箍系数变化关系图Fig．9 The concern curve of peak impact force and the confinement index

图10是三桩结构(桩管厚3.5，桩管内混凝土为C40)的Ⅰ和Ⅱ位置在桩心距分别为400、500、600、700受10 m/s球撞击的冲击力变化图。

图10 冲击力峰值随桩心距变化关系图Fig．10 The concern curve of peak impact force and distance of pile center

从图8可看出冲击力峰值随着混凝土强度的提高而增大，且近似成线性关系，Ⅰ处增幅达1.1%，Ⅱ处增幅达3.7%，原因在于混凝土强度提高，使得它迟于屈服，使得它抗压缩变形的能力提高。从图9可看出冲击力峰值随着混凝土套箍系数的提高而增大，且Ⅱ位置比Ⅰ位置明显，原因在于桩管壁厚增加，使得它对混凝土的约束效应加大，使得截面的抗弯刚度提高。从图10可看出冲击力峰值在Ⅱ处随桩心距增大变化不明显，但在Ⅰ处随桩心距增大而减小，降幅约达2.2%，原因是Ⅰ处桩心距增大，梁管并不是无限刚、不可压缩的，削弱了桩之间的协同变形，使得Ⅰ位置在相同的冲击能量下随着桩心距增大易于变形。

3.3 应力应变分析

下面就对三桩结构(桩管厚3.5，桩心距取600 mm)的Ⅰ和Ⅱ位置分别受直径300 mm刚球10 m/s速度撞击这两种工况进行应力应变分析，应力云图分别如图11和12所示。应力采用Von Mises应力，应变采用有效塑性应变。

图11 工况一Von Mises应力云图Fig．11 Von Mises stress nephogram under the working condition one

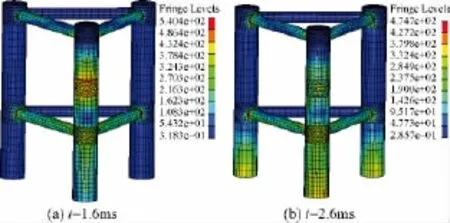
图12 工况二Von Mises应力云图Fig．12 Von Mises stress nephogram under the working condition two

从图11与图12可看出，三桩结构Ⅰ和Ⅱ位置受到撞击时，冲击动力响应迅速向周围传递，Ⅰ位置通过与之相连的两根梁管向后桩进行传递，另外通过前桩向下传递，前桩底端比后桩底端先出现响应;Ⅱ位置沿着上下方向传递，并通过与之相连的上下梁管传到后桩上，另外通过前桩向下传递。前桩的应力比后桩的应力大，受冲击部位、桩梁节点处、桩底部应力相对其他位置来说较大，符合结构在冲击作用下的受力特征。

图13 控制点布置图Fig．13 Arrangement of control points

表2 单元应力应变值Table 2 Unit stress and strain value

在工况一与工况二下，三桩结构的内应力与应变均是对称的，后桩控制点仅在一个上面取，控制点如图13所示。由表2可知，钢最大应力与有效塑性应变以及混凝土最大应力与有效应变均出现在受冲击部位，且工况二的钢有效应变比工况一大，混凝土最大应力相反，原因在于受冲击的3位置上下相邻的约束比1位置强，使得3位置的钢材比1位置耗能多，同时使得3位置处的混凝土受挤压程度比1处小。除受冲击部位应力大外，5、7、10、11、13、15、17 处应力也较大，原因在于桩梁节点处应力复杂，三桩结构对冲击的抵抗最终要靠桩根部的约束，建议在桩梁节点处与桩根部应该加强，以提高结构在块石撞击下的整体性、局部的抗破坏能力和耐久性，可以采取的简单措施有在桩梁节点焊接处沿梁管的环向焊上加劲肋和在桩的根部沿环向焊上加劲肋。梁管的中部点14、16、18以及桩的8等非直接受冲击部位处应力较小。从6到7以及9到10应力应变均呈增大趋势，可看出结构在底部呈现出典型的悬臂特征。从7、10点钢的有效塑性应变大小看出，前桩受撞击时，前桩根部耗能比一个后桩的多，且工况二的前后桩钢有效塑性应变差值大于工况一的。工况一的4、8、16点尽管钢最大应力超过235 MPa，但未出现塑性应变，原因在于钢采用的是CP模型，屈服应力随着时间是变化的，这些点当达到最大应力的时候，该时刻的屈服应力高于它们的最大应力。工况一、二的7、10点处应力不特别大，但是塑性应变还不小，原因在于冲击结束后三桩结构左右振荡，使得桩的根部频繁进入塑性，产生塑性变形积累所致。

4 结论

(1)结构不同部位的冲击力时程曲线存在着显著差异。同一冲击速度下，Ⅱ处冲击力峰值约为Ⅰ处的1.12倍，表明受冲击部位的约束越强，即局部刚度越强，则冲击力峰值越大;冲击速度的增大、混凝土强度等级的提高以及桩截面套箍系数的增大均会增大冲击力峰值，且相较于后两个因素，冲击力峰值对冲击速度的变化更为敏感;顶部节点处的冲击力峰值随着桩心距的增大而减小。

(2)受冲击部位背面的残余变形与冲击速度近似成二次关系，与冲击能量成线性关系。

(3)冲击荷载作用下，结构不同部位的响应不同，其中，受冲击部位的应力应变最大，钢材应力达到578.95 MPa，有效塑性应变达到0.0625，混凝土应力达到194.56 MPa，有效塑性应变达到0.0428，设计时应予以加强，此外，桩梁连接处以及桩支座处的响应也较大，同样需要引起注意。

［1］赵健.我国泥石流防治措施研究［J］.中国水利，2007，14:50-52.ZHAO Jian.Research of debris flow preventing and controlling measures in China［J］.China Water Resources，2007，14:50-52.

［2］陈继华，王秋军，张彦林.泥石流防治研究［J］.科技广场，2011(2):20-22.CHENJihua， WANG Qiujun， ZHANG Yanlin.Debris flow prevention and control research［J］.Science and Technology Square，2011(2):20-22.

［3］李德基.透水型拦挡坝在泥石流防治中的应用［J］.中国地质灾害与防治学报，1997，8(4):60-66.LI Deji.Application ofpermeable blocking dam indebris flow prevention［J］.The Chinese Journal of Geological Hazard and Control，1997，8(4):60-66.

［4］钟善桐.钢管混凝土结构在我国的应用与发展［J］.建筑技术，2001，32(2):80-82.ZHONG Shantong.Application of developmentin china ofconcrete filled steeltubularstructure［J］.Architecture Technology，2001，32(2):80-82.

［5］王蕊，李珠，任够平，等.钢管混凝土梁在侧向冲击荷载作用下动力响应的试验研究和数值模拟［J］.土木工程学报，2007，40(10):34-40.WANG Rui， LIZhu， REN Gouping， etal.Experimental study and numerical simulation of the dynamic response of concrete filled steel tubes under lateral impact load ［J］.China Civil Engineering Journal，2007，40(10):34-40.

［6］李珠，王瑞峰.固简支钢管混凝土构件侧向冲击试验研究［J］.工程力学，2008，25(增1):193-197.LI Zhu，WANG Ruifeng.Experimental study of fixedfreely supported concrete filled steel tubular under lateral impact load［J］.Engineering Mechanics，2008，25(S 1):193-197.

［7］DZ/T0239—2004泥石流灾害防治工程设计规范［S］.DZ/T0239—2004 Debris flow disaster prevention and control of engineering design specifications［S］.

［8］吴积善，等.云南蒋家沟泥石流观测研究［M］.北京:科学出版社，1990:63-155.WU Jishan，et al.Observation and study of debris flow of Jiang Jia Ditch in Yunnan［M］.Beijing:Science Press，1990:63-155.

［9］任够平，李珠，王蕊.低速侧向冲击下钢管混凝土柱挠度研究［J］. 工程力学，2008，25(5):170-175.REN Gouping，LI Zhu，WANG Rui.The Deflecti-on of concrete filled steel tubular column under lateral at low speed［J］.Engineering Mechanics，2008，25(5):170-175.

［10］GB50010—2010混凝土结构设计规范［S］.GB50010—2010 Code for design of concrete structures［S］.