模糊数学在缓倾顺向边坡稳定性判别中的应用

刘光华，张 玲，赵 鹏，熊 超

(1.重庆交通大学岩土工程研究所，重庆 400074;2.重庆市地质灾害防治工程勘查设计院，重庆 400700)

0 引言

岩层走向与边坡面走向之间的夹角在30°之内的边坡称为顺向边坡［1］，工程中常将岩层倾角为15°～30°的顺向边坡称为缓倾顺向边坡。

缓倾顺向边坡受到地质作用和人为作用由稳定状态逐渐发展至失稳破坏。目前评价缓倾顺向边坡的稳定性状态主要采用单一滑面的极限平衡法及强度折减法，但是这些精确的数学模型中，都有预先假定的前提条件，这种假定本身就与客观实际存在一定差异，对于影响因素较多且不明确的复杂事物，运用模糊数学理论得到的结果往往更贴近实际［2］。

1 缓倾顺向边坡破坏阶段分析

缓倾顺向边坡在边坡开挖面处临空失去支挡、后缘和侧边界抗拉强度及侧摩阻力降低的情况下，容易产生沿强度较低的层面或软弱结构面向临空面方向发生滑移失稳破坏，如重庆市武隆县铁矿乡鸡尾山山体崩滑特大地质灾害［3］。

该类型边坡从形成、发育直至最终失稳破坏通常需要较长的时间，一般需经历三个阶段:

1.1 形成阶段

地质构造作用形成缓倾顺向边坡初始形态，此时边坡安全储备较高(图1)。

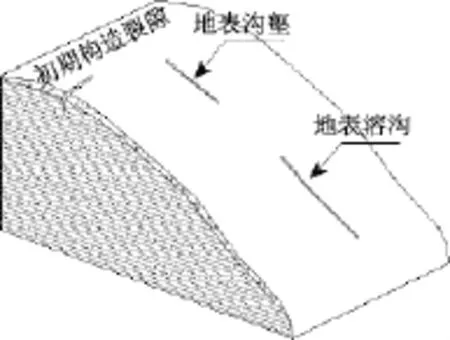
图1 缓倾顺向边坡形成阶段Fig．1 The formation stage of gently slant slope

1.2 发育成熟阶段

在长期的地质作用及人类工程活动(前缘因工程活动开挖或采矿活动)共同影响下，缓倾顺向边坡已形成贯通率较高的后缘裂隙和侧边界，加之雨季裂隙赋水下渗降低软弱结构面抗剪强度，此时缓倾顺向边坡处于基本稳定-欠稳定状态(图2)。

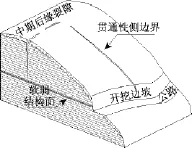
图2 缓倾顺向边坡形成阶段Fig．2 The mature stage of gently slant slope

1.3 滑移失稳破坏

在降雨进一步降低软弱结构面强度及裂隙贯通率不断提高，边坡最终失稳发生沿临空面方向的滑移破坏(图3)。

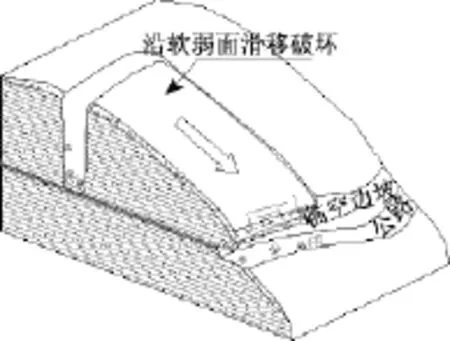
图3 缓倾顺向边坡形成阶段Fig．3 The gently slant slope slide to destory

2 缓倾顺向边坡权重分析

由上述形成阶段分析，缓倾顺向边坡在后缘裂隙形成、侧边界贯通性较好、软弱结构面强度较低、降雨作用较强及人类工程活动较强5种主要条件存在时，缓倾顺向边坡将可能发生失稳破坏，如图4影响因素权重相互作用关系分析。

图4 影响因素权重相互作用关系分析Fig．4 Analysis of factors interaction

通过上述权重分析，不难发现缓倾顺向边坡失稳坡坏是自然因素和人为因素共同作用的结果，在自然因素中，降雨是影响最大的作用因素;人为因素中，以前缘开挖、采矿活动等为强影响因素。

重庆武隆鸡尾山特大滑坡滑移破坏之前，一直有采矿活动，开采区位于边坡下部二叠系下统梁山组(P1l)的含铁矿层，形成面积约5×104m3的采空区，导致前缘关键块体应力状态发生改变，最终受岩溶发育带瞬时脆性剪断［4］。

前缘开挖导致边坡失去支撑，初始应力场发生改变，影响边坡应力状态的同时降低了边坡的稳定性，根据工程经验，顺向边坡因前缘开挖应力状态的影响范围约为前缘开挖高度的6.5倍［5］。

由上述分析，降水作用和工程活动是降低顺向斜坡的两个主要因素，但是对其进行稳定性评价时，应该根据这两个因素现阶段对五个条件的影响程度，进行稳定性综合评判，通常各个条件的权重所占比例:

根据边坡所处地质环境，各因素所占权重不同，应当进行权重分析与经验相结合取值。

3 模糊数学法［6］的应用

3.1 建立因素集

因素集是影响边坡稳定状态的所有因素构成的集合。表示为:

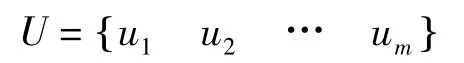
3.2 建立权重集

根据边坡的实际情况，确定不同因素所占的权重值，从而建立权重集

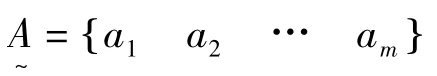
3.3 建立备择集

备择集是评判对象可能出现的所有评判结果。

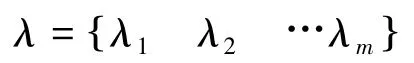
3.4 单因素评判

单独从某一个因素出发，确定各离散值对备择集的隶属程度，得出各单因素评判集为:

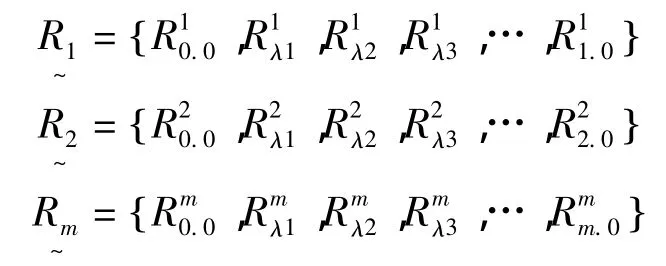
评判矩阵为:

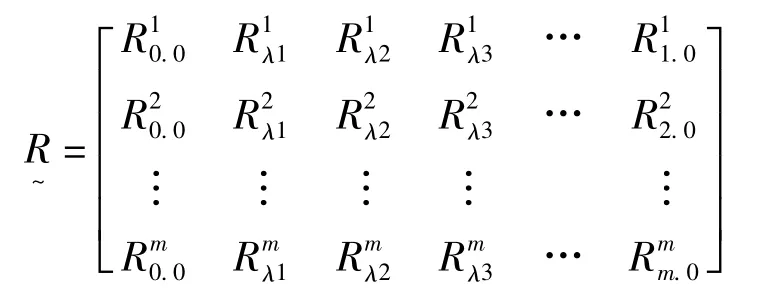
3.5 模糊综合评判

权重集与单因素模糊评判矩阵的乘积可以有效地反应所有因素对判定对象的综合影响。对模糊综合评价做如下表示:

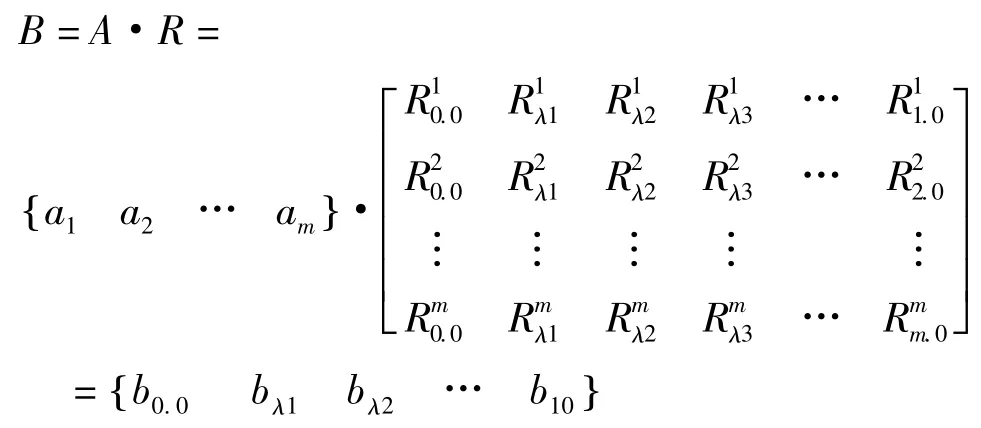
3.6 稳定性系数确定

得到评判指标B之后，需要对其进行合理的后处理以得到最终评判指标。处理评判指标主要有最大隶属法、模糊分布法、加权平均法等。对于边坡稳定性系数这类定量型评判对象，常采用加权平均法对其进行评判指标后处理。

4 工程实例

4.1 工程概况

重庆市武隆县天生三桥景区拟迁建观光电梯，新建电梯场址地处一缓倾顺向边坡下方，该顺向边坡所在区域属构造溶蚀中山地貌，西南边坡地形陡峭，总体坡向232°，坡度 75°～90°，基岩裸露，植被不发育，局部边坡面较平直，西南侧边界已完全形成(图5)。

图5 武隆天生三桥缓倾顺向边坡照片Fig．5 The photograp of gently slant slope in Wulong Tiansheng bridge

边坡灰岩呈灰色、黑灰色，隐晶质结构，薄-中厚层状构造，夹泥质灰岩(相对软弱夹层)，厚度0.1～0.3 m。

场地地下水类型为孔隙水和岩溶水，孔隙水赋存于边坡顶部、边坡下部斜坡第四系残坡、崩坡积土层中，含水层具有结构松散、透水性好的特点，受地形条件及本身土体结构影响，无统一地下水位，其赋水性差，主要靠大气降水补给，以孔隙为通道渗透地下，排泄于场地下方低洼冲沟处，雨季含水量稍大，旱季少水或无水。

缓倾顺向边坡基座处分布有两层沿层面的相对软弱夹层R1和R2，见少许光滑擦痕，系构造作用产生，在强度不断降低的情况下可视为该顺向边坡的潜在滑移面。相对软弱夹层R1和R2均为泥质灰岩构造，属硬性结构面，R1与R2法向间距5.1 m，两处夹层均有植被发育。

4.2 极限平衡法稳定性评价

根据地质灾害防治工程勘查规范［7］判定该缓倾顺向边坡稳定性状态，计算简化模型如图6。

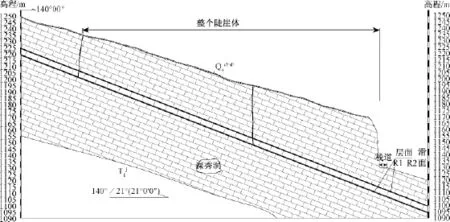
图6 武隆天生三桥缓倾顺向坡典型剖面图Fig．6 The typical profile of gently slant rock slope in Wulong Tiansheng bridge

由于现场进行大型直剪试验难度较大，试验时间较长，加之相对软弱夹层较薄极可能导致试验结果工程意义不大［8］，所以对相对软弱夹层的抗剪强度取值参照建筑工程边坡技术规范［9］查表取值。

表1 相对软弱夹层抗剪强度参数取值Table 1 The shear strength of relatively weak interlayer

依据重庆市地方标准—地质灾害防治工程勘察规范稳定性计算公式:

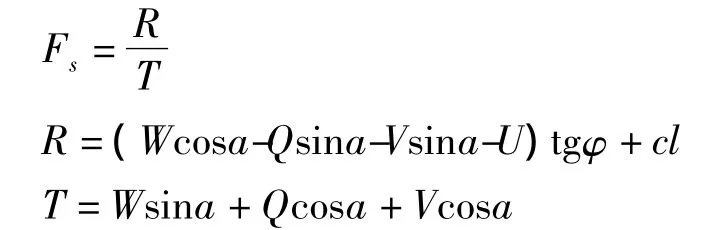
式中:R——滑坡抗滑力/(kN/m);

T——滑坡下滑力/(kN/m);

W——滑坡体自重与建筑等地面荷载之和/(kN/m);

a——滑坡体或及其某条块滑面倾角/(°);

C——滑面粘聚力标准值/kPa;

l——滑坡体或其某条块滑面长度/m;

V——后缘裂隙水压力/(kN/m);

U——滑面水压力/(kN/m);

Q——作用于滑坡体或其某条块的地震力/(kN/m);

φ——滑面内摩擦角标准值/(°)。

经计算，该缓倾顺向边坡在暴雨工况下处于稳定状态，沿潜在滑动面R1、R2及一般层面的边坡整体稳定性系数分别为 1.266、1.291、1.794。

4.3 稳定性状态定性分析

仅根据经验取值判断该缓倾顺向边坡的稳定性状态显然是不够充分的，需对边坡进行定性综合的评价。

从地质环境演变历史过程来看，边坡正处于侧向层层崩塌的后退式边坡时期，西南侧边坡坡度大于80°，且部分崖面下部较上部崩塌进程快，崖面处于倒悬状态。现阶段相对软弱夹层强度较高，属硬性结构面，相对软弱夹层见少许因构造作用产生的擦痕，后缘裂隙深度较浅，贯通情况一般，且裂隙宽度不大，主要是地表流水冲刷形成的溶蚀裂隙和边坡卸荷形成的卸荷裂隙;边坡顶部见沿沟底发育的四个落水洞，但未发现落水洞之间串联组成的贯通性构造裂隙，边坡体前缘临空侧未见鼓胀裂隙及挤出现象。综上判断，在现状条件下，边坡整体处于整体稳定状态。

4.4 模糊数学对天生三桥缓倾顺向边坡分析

4.4.1 建立因素集

影响缓倾顺向边坡的稳定性系数值k的因素集为:

4.4.2 建立权重集

根据武隆天生三桥缓倾顺向边坡所处地质环境，可以对侧边界、后缘裂隙及结构面强度进行权重分析(降水作用及人类活动在此处不便统计所以依据经验取值):

(1)侧边界权重分析

天生三桥边坡北东侧边界未贯通段提供的剪力作为抗滑力，此处主要分析边界贯通率的变化对边坡稳定性状态的敏感程度，以此判断侧边界贯通率在权重集中的权重值(表2)。

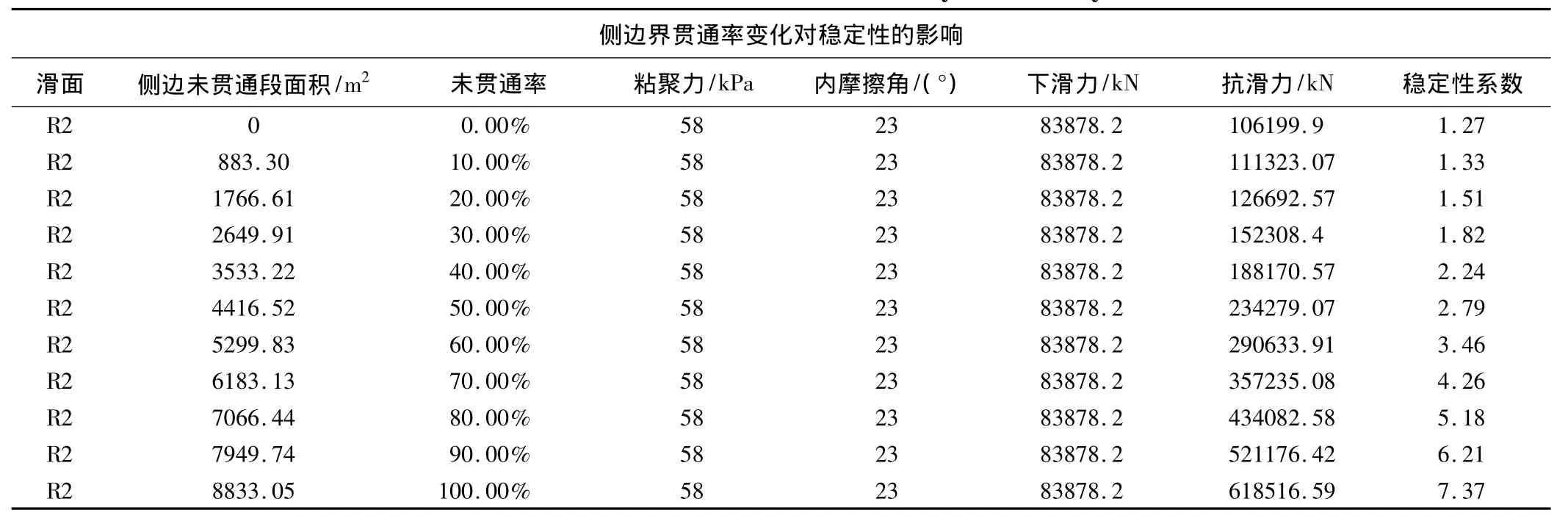
表2 侧边界权重分析数据表Table 2 The data sheet of lateral boundary factor analysis

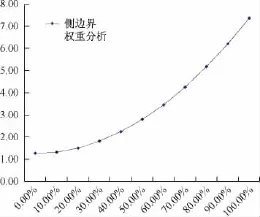
图7 侧边界权重分析图Fig．7 The chart of lateral boundary factor analysis

现阶段边坡侧边界贯通率较低(90%未贯通)，侧边界近期变化对稳定性状态影响较大，所以综合考虑侧边界权重取值0.20(图7)。

(2)后缘裂隙权重分析

针对后缘裂隙未贯通段对潜在滑移边坡体提供拉力即抗滑力，此处考虑不同后缘裂隙贯通率对边坡稳定性状态的敏感程度(表3)。

现阶段后缘裂隙贯通率一般(70%未贯通)，侧边界近期变化对稳定性状态影响一般，所以综合考虑测边界权重取值0.15(图8)。

(3)结构面强度权重分析

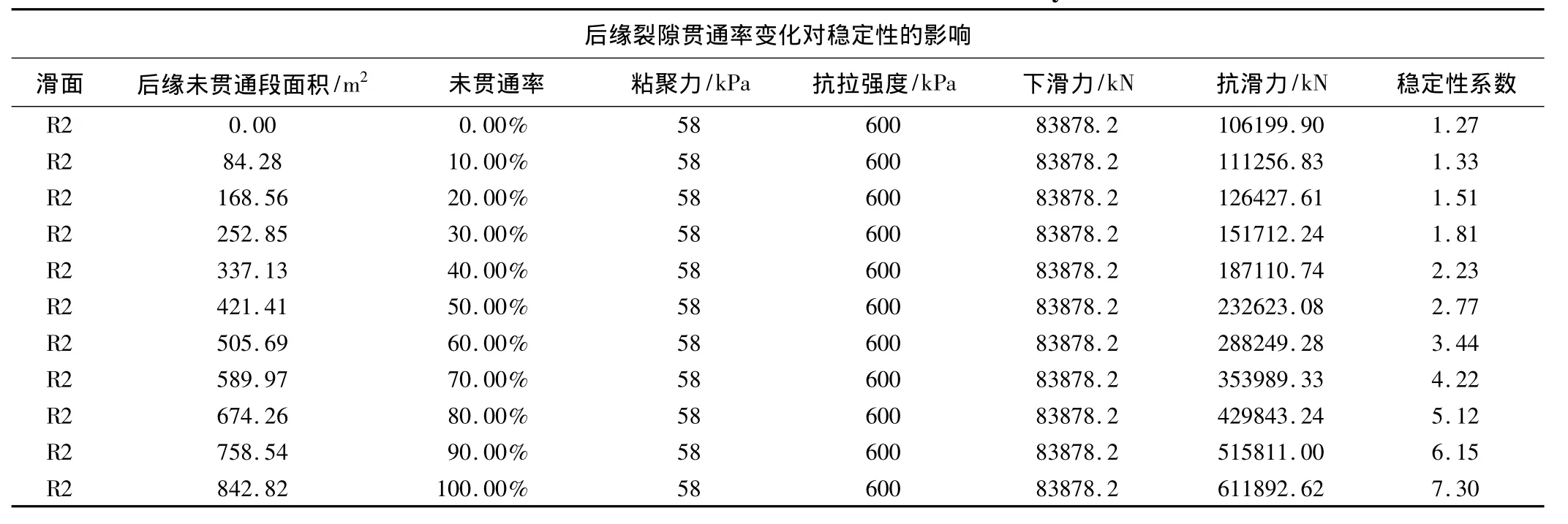
表3 后缘裂隙权重分析数据表Table 3 The data sheet of backside fracture analysis

结构面强度主要包括粘聚力和内摩擦角，此处为了便于研究单一因素的权重，将结构面强度转化为等效内摩擦角进行分析(表4)。

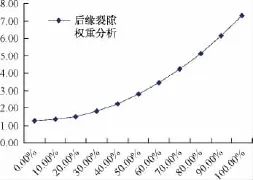
图8 后缘裂隙权重分析图Fig．8 The chart of backside fracture factor analysis

依据规范的结构面强度取值(C=58kpa，φ=23°)等效之后的内摩擦角为74.54°。由图9分析，在等效内摩擦角为74.54°邻域内稳定性变化是十分明显的，可以认为结构面强度占较大权重，取值0.25。

此外，由于降水作用直接影响侧边界、后缘裂隙及结构面强度，所占权重也应按较重处理，取值0.25;人类工程活动在该边坡所处位置影响作用一般，主要为栈道开挖，所以权重值取0.15。

综上所述，权重集为:

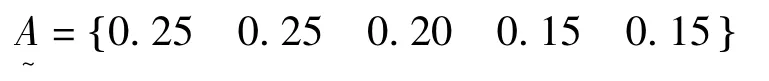
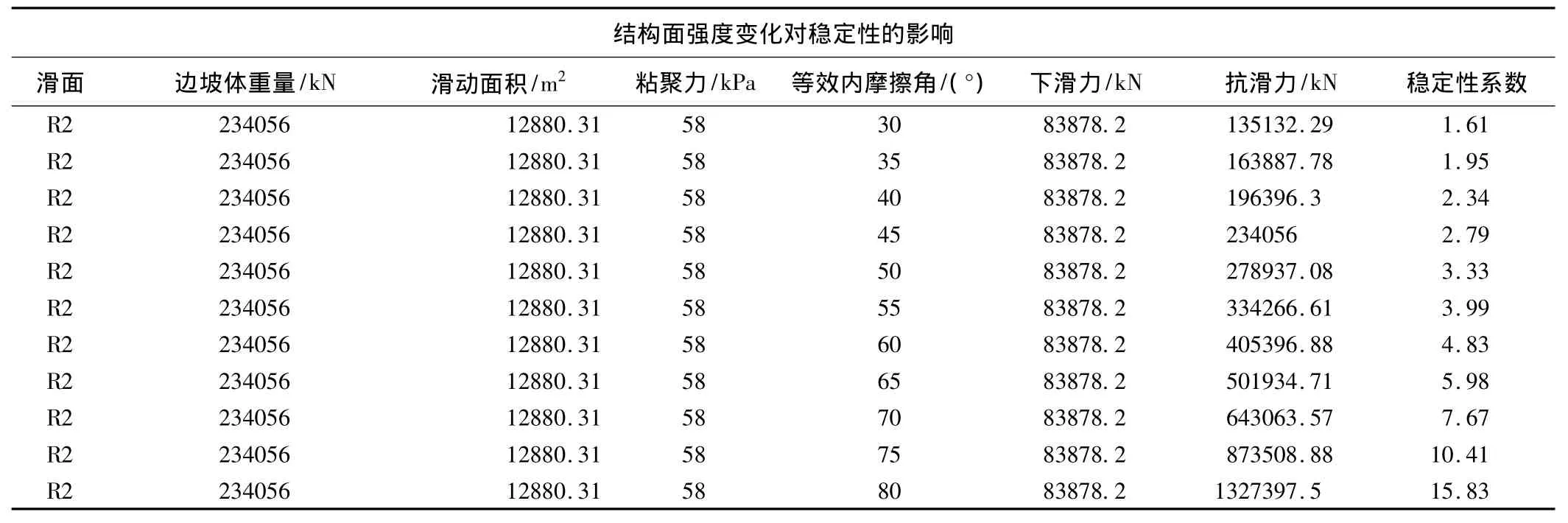
表4 结构面强度权重分析数据表Table 4 The data sheet of strength of structural plane analysis

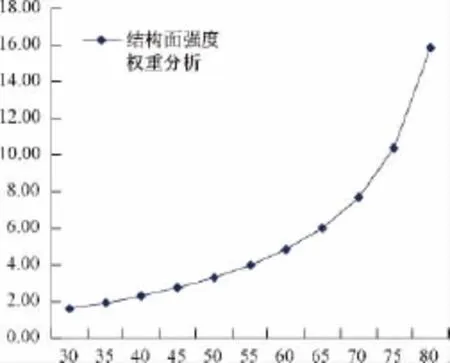
图9 结构面强度权重分析图Fig．9 The chart of strength of structural plane factor analysis

4.4.3 建立备择集

备择集是评判对象可能出现的所有评判结果。一般顺向边坡的稳定系数区间为［1.00，2.00］，按等步长(d=0.20)均布取值，建立备择集:

4.4.4 单因素评判

单独从某一个因素出发，确定各离散值对备择集的隶属程度，得出各单因素评判集为:

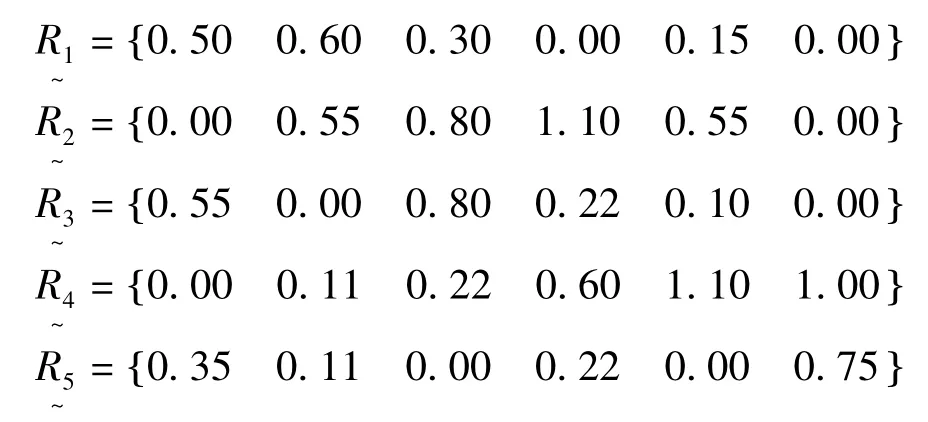
所以评判矩阵为:

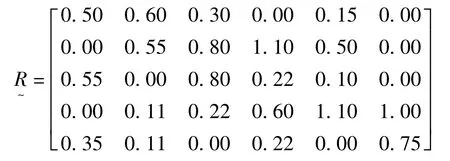
4.4 .5 模糊综合评判

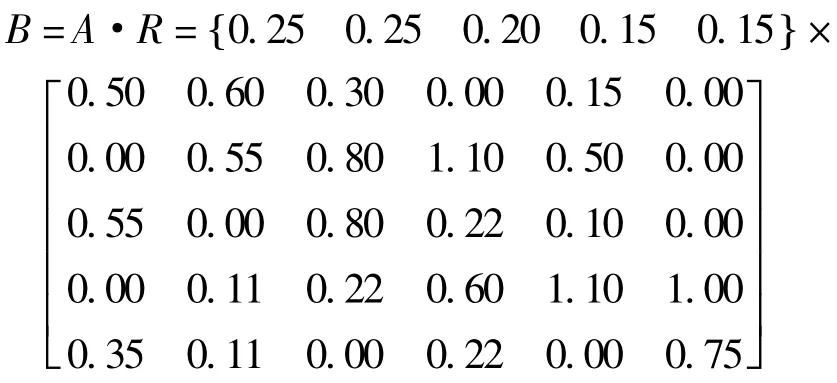
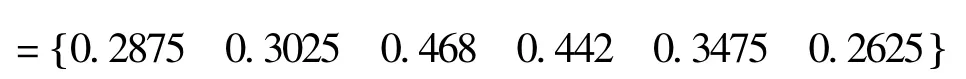
4.4.6 稳定性系数确定

通过加权平均求得:

模糊数学分析结果与规范法及稳定性定性评价结果基本一致，可以认为该缓倾顺向边坡目前处于稳定状态，与边坡现阶段实际情况也基本吻合。

5 结论

(1)缓倾顺向边坡受季节性降雨、人类工程活动或采矿活动作用，后缘裂隙扩展、侧边界逐渐贯通及软弱结构面强度降低，易产生滑移失稳破坏。

(2)模糊数学在进行权重分析时，不同边坡其影响因素所占权重也不尽相同，应根据权重分析并结合工程经验进行取值，做到具体边坡具体分析。

(3)正确判定某一缓倾顺向边坡目前所处的稳定状态，应经过规范、定性分析及模糊数学等方法进行综合判定分析，所得到的稳定性评判结果更贴近实际。

［1］白云峰，周德培，冯君.顺向边坡岩层走向与边坡走向夹角的上限值［J］.西南交通大学学报，2005，40(3):326-329.BAI Yunfeng，ZHOU Depei，FENG Jun.Upper limit of angle between strikes of slope and strata for dip slope［J］.Journal of Southwest Jiaotong University，2005，40(3):326-329.

［2］肖盛燮，王平义，吕恩琳.模糊数学在土木与水利工程中的应用［M］.北京:人民交通出版社，2004:1-2.XIAO Shengxie， WANG Pingyi， LUE Enling.Application of fuzzy mathematics in the civil and hydraulic engineering ［M］. Beijing:China Communications Press，2004:1-2.

［3］高杨，殷跃平，邢爱国，等.鸡尾山高速远程滑坡—碎屑流动力学特征分析［J］.中国地质灾害与防治学报，2013，24(4):46-51.GAO Yang，YIN Yueping，XING Aiguo，et al.Analysis of Jiweishan landslide debris flow-high speed and long distance features［J］.The Chinese Journal Geological Hazard and Control，2013，24(4):46-51.

［4］殷跃平.斜倾厚层山体滑坡视向滑动机制研究——以重庆武隆鸡尾山滑坡为例［J］.岩石力学与工程学报，2010，29(2):218-226.YIN Yueping.Mechanism of apparent dip slide of inclined bedding rochslide-a case study of jiweishan rockslide in Wulong，Chongqing［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(2):218-226.

［5］李安洪，周德培，冯君，等.顺层岩质边坡稳定性分析与支挡防护设计［M］.北京:人民交通出版社，2011:99-104.LI Anhong，ZHOU Depei，FENG Jun，et al.Analysis of stability ofrock bedded slope and retaining protection design［M］.Beijing:China Communications Press，2011:99-104.

［6］欧国林，张娜.模糊数学法在路基边坡稳定性评价中的应用［J］.岩土工程与地下工程，2009，29(1):67-68.OU Guolin，ZHANG Na. Application offuzzy mathematics in evaluation ofslope stability［J］.Geotechnical Engineering and Underground Engineering，2009，29(1):67-68.

［7］DB50/143—2003重庆市地方标准地质灾害防治工程勘察规范［S］.DB50/143—2003 Code for investigation of geological disasterprevention projectoflocalstandard in Chongqing［S］.

［8］杨朝发，刘发祥.综合评价法确定岩质顺向坡软弱结构面的强度参数［J］.探矿工程(岩土钻掘工程)，2012，39(8):72-78.YANG Chaofa，LIU Faxiang.Determination of strength parameter of weak structural plane of consequent rock slope by comprehensive evaluation method ［J］.Exploration Engineering (Geotechnical Drilling Engineering)，2012，39(8):72-78.

［9］GB50330—2002建筑边坡工程技术规范［S］.GB50330—2002 Technical code for building slope engineering［S］.