顺层岩质边坡滑动面确定方法探讨

韦 达，赖 勇

(重庆交通大学河海学院(重庆)，重庆 400074)

0 引言

顺层岩质边坡是在公路、铁路路堑开挖、工民建中的基坑施工［1］以及自然滑坡中常遇到的一种边坡［2-3］。在分析和研究岩质路堑边坡的稳定问题时，首先遇到的问题之一便是确定潜在滑动面。这也是能否正确进行稳定性分析的关键。但是，在岩质边坡中，影响滑动面位置的因素有很多。诸如交错的节理、断层、软弱结构面［4］等。在这些潜在的滑动面中，找出关键的控制性滑动面，这对于接下来的边坡稳定性分析和计算至关重要。在现阶段的研究中，主要根据工程地质调查来初步确定岩质边坡的可能滑动面，再通过计算来进一步确定最不利滑面。

胡其志等［5］分析了顺层岩质边坡中地下水力的作用。地下水力作用主要是沿结构面分布的拖拽力和裂隙水压力，在对控稳结构面的分析中，滑动面上的扬压力、张裂隙静水压力以及拖拽力的大小均取决于后缘张裂隙的充水高度。地下水对边坡的稳定性主要与静水压力有关。同时，路为等人［6］依据平面刚体模型，导出了滑移-拉裂的失稳判据。得出当边坡高度大于临界值时，将产生失稳。在根据水力-驱动型滑坡模型计算时，边坡的后缘充水高度也是影响边坡失稳的重要因素。在考虑到边坡软弱夹层对其稳定性的影响时，曹兴松等［7］将内部的软弱带视为刚性体，利用机动法和能量系数方法进行稳定性研究分析。其结果表明该方法具有可行性和实用性。王根龙［8］等人还根据外力所做的功与内力所消耗的功这一相等关系，用极限分析上限法对平面滑动型岩质边坡进行了分析，其研究结果表明该理论有较好的实用性。

在考虑到顺层滑移-拉裂边坡时，滑动岩体的范围是着重考虑分析的基础。冯君等人［9-10］考虑了开挖卸荷效应对岩体参数的影响，并且建立了相应的滑动范围计算式。在滑动体范围确定的情况下，分析计算失稳岩层的临界长度，便可判断边坡的稳定性。

可见，在不同的变形破坏形式下，岩质边坡的破坏有所不同。本文就主要的几种破坏形式下对顺层岩质边坡滑动面进行探讨分析。

1 工程地质归类

根据工程地质勘查报告和现场的勘查结果，对边坡所在的区域进行分析，比较其在地质历史过程中所形成的构造特征、应力场。根据特征确定活动断裂带，并判断它对开挖边坡的影响。

在分析中侧重考虑以下几个方面:

(1)结构面的组成。比如结构面的充填物质，含水情况，发育情况，以及结构面与岩层的结合情况等。

(2)缓倾结构面与边坡走向的关系。冯君［9-10］等研究表明，当结构面走向和边坡走向超过30°时，对边坡稳定的影响便可不计。

(3)当几组优势结构面的倾向与边坡呈缓倾时，这时要尤为重视。

2 不同破坏类型的滑动面确定

2.1 顺层滑动破坏

2.1.1 单一滑面

单一滑面顺层滑动是指顺层边坡中只有一条明显的软弱结构控制面，通过地质勘查可以明确地确定。

当坡面平缓，有较发育的垂直节理时，需要考虑水的作用。侵入坡体的水不仅造成岩体的物理化学性质发生变化，引起岩体的收缩或膨胀，强度降低。而且，侵入岩体软弱夹层的水还对滑动面起到润滑作用，致使滑动面的强度降低，抗滑力下降，同时，这些侵入的水还会产生附加荷载，计算时需要根据节理裂隙的发育情况考虑浮托力，水压力及渗透力等。具体的计算推导可参见相关文献［5-9］。

2.1.2 多层滑面

通过前期地质调查，勘明在岩体边坡内有多条软弱带，这些软弱带对边坡的稳定都有影响，在考虑这些软弱夹层的影响时，仅仅将边坡体看成是刚性体来分析是与实际有出入的［2］。在考虑这些影响时，可以通过机动位移法［7-8］或是极限平衡法进行计算，选出最不利滑面。

机动位移法的理论基础是塑性力学极限分析中的上限定理。上限定理规定在所有的与机动许可速度场所对应的荷载中，物体破坏时，极限荷载最小。这时，外荷载做的功就是塑性变形机构中所耗散的能。将边坡看成是刚塑性体，计算荷载所做的功和塑性变形机构的内能耗散，通过比较，就能判断边坡所处的状态，进而对边坡的稳定性做出分析。

假设计算模型如图1所示:

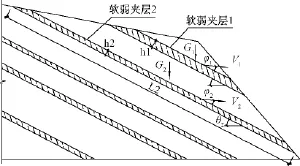
图1 岩体计算模型Fig．1 The calculation model of rock mass

图中的G1，G2表示滑体重，γ1，γ2表示滑带重度，c、φ分别表示粘聚力与内摩擦角。在该模型中，软弱夹层1的速度从上表面的V1变化到下表面的V2，可以假设软弱夹层1看成为一系列的速度间断面，假定各速度间断面之间的法向速度不变，切向速度按线性变化，则它便满足了机动许可速度场的要求。用下标V表示法向速度，S表示切向分量，则:

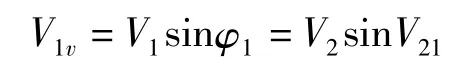
软弱夹层1上表面的切向速度分量是V1s=V1cosφ1，下表面为V2s=V2cosφ21。φ21表示滑体 2 的速度V2与软弱夹层的夹角。则切向速度场的变化如下:

当 φ1＜φ21时:

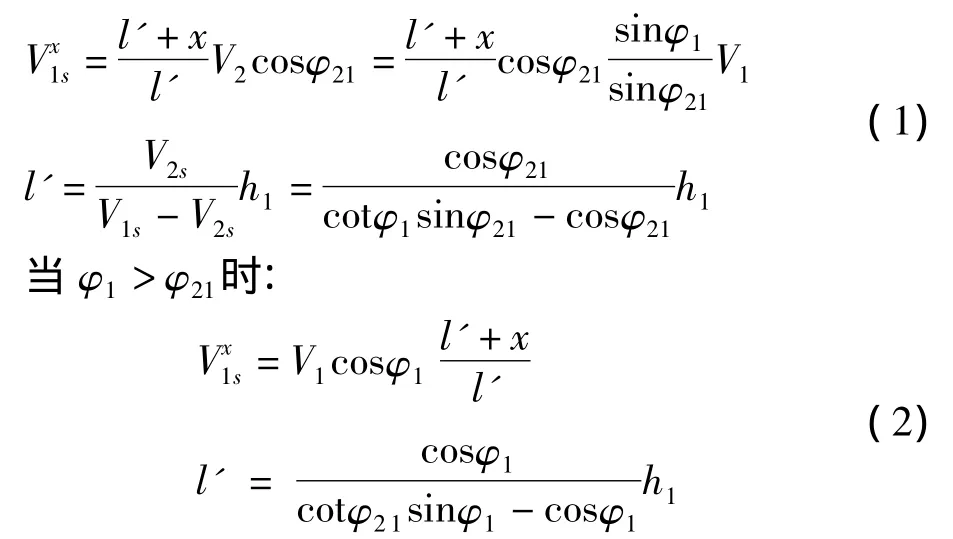
所以，根据式1与式2，滑体1只在重力作用下的外力功率为:

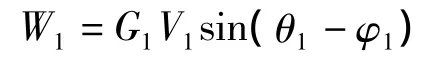
滑体2的外力功率为:

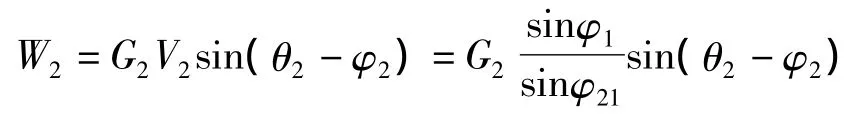
同时，滑带1的外力功率为:

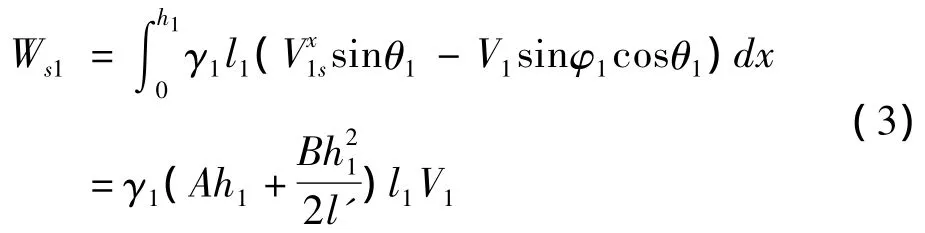
当 φ1≤φ21时:A=B-sinφ1cosθ1

B=sinφ1sinθ1cotφ21

当 φ1＞φ21时:A=sin(θ1-φ1)

B=cosφ1sinθ1

因为系统的内能耗散主要是在滑带之间，因此滑带1的内能耗散率D's1为:

当 φ1＜φ21时:

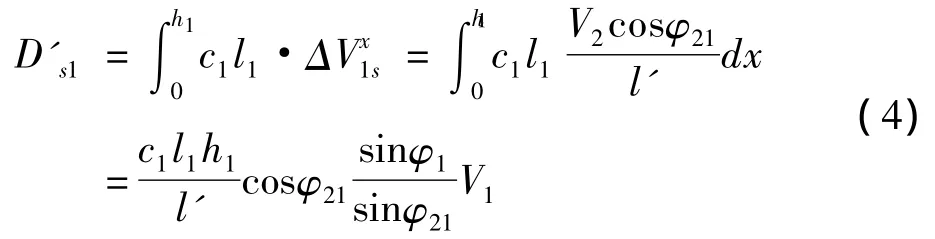
当 φ1＞φ21时:

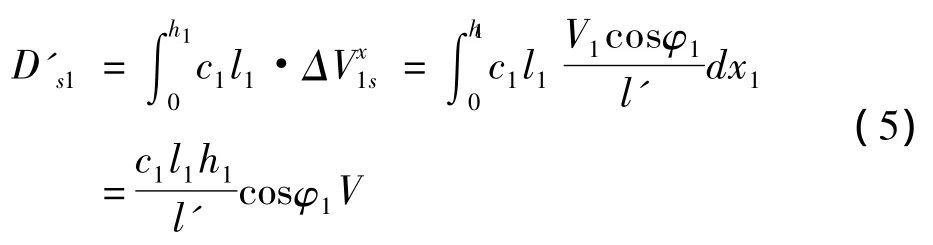
滑带2的内能耗散率为:

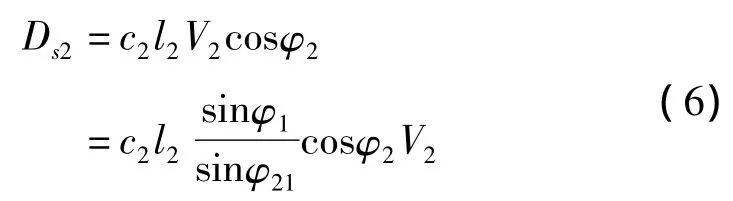
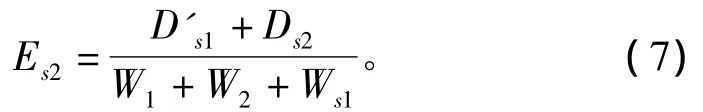
如若有多层的滑面，用同样的方法计算每个Esi。因此，Es便是边坡失稳的判别依据。通过计算每个滑带的能量系数，比较最小的便是最不稳定的滑动面;当Es小于1时，边坡将失稳。

2.2 滑移拉裂破坏

在边坡开挖中，当所处的岩层倾角较小，开挖坡面倾角较大时，将不可避免的要切断岩层。而当岩层满足缓倾条件时，斜坡上的岩体将沿软弱层面向开挖临空面滑动，导致滑移体拉裂破坏。具体的破坏情况取决于岩体结构面的产状和岩石力学特性。软弱结构面的上岩体的下滑力超过了结构面的抗滑力后，将后缘拉裂，发生破坏。其中岩体的横向失稳长度将是控制岩质边坡滑动面的关键因素。

在有多个软弱结构面的顺层缓倾岩质边坡中，可简单的将其分为两种情况讨论［10］，即天然边坡角等于岩层倾角和天然边坡角小于岩层倾角。

因此，根据式3到式6，由能量系数可得:

在开挖边坡段分析，通过ABC和AB’C’岩体的极限平衡状态，即块体的下滑力等于抗滑力:

由此，可以计算得到顺层边坡失稳时的横向极限长度LHi:

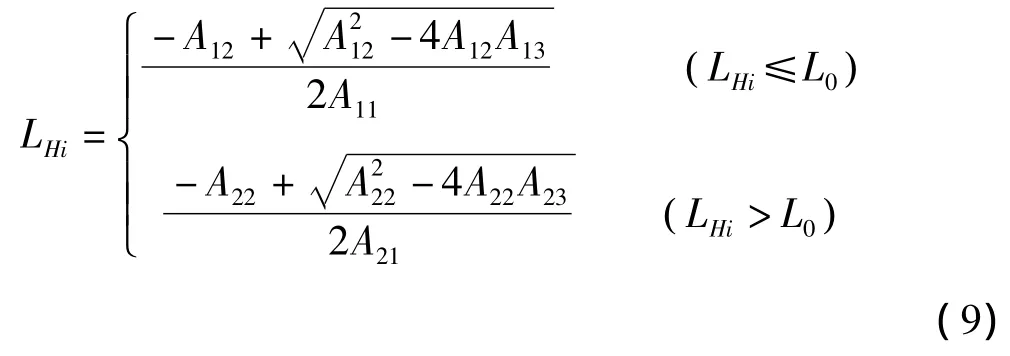
其中:L0表示力学参数弱化区

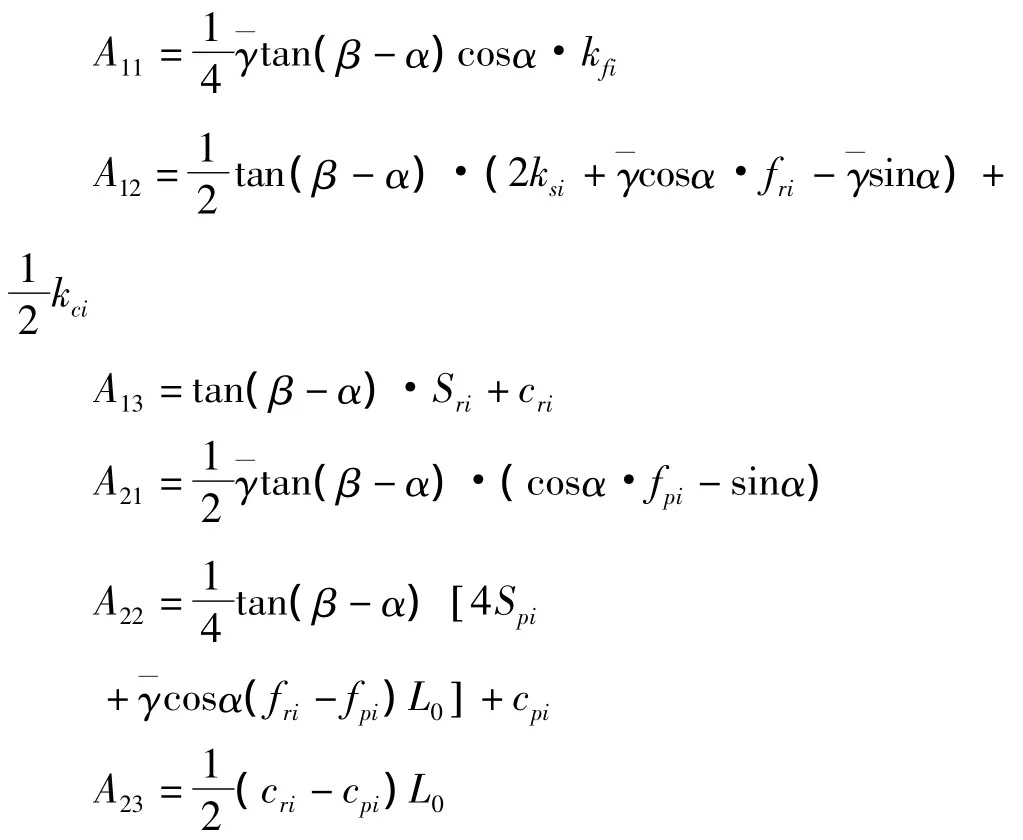
用f、c、S分别表示摩擦系数，黏结力及等效抗拉强度;它们的下标p、r分别表示在相应的天然状态下和受扰动的情况下;用kfi、kci、Ssi表示其折减值。

在自然坡段的情况下，分为两种情况下，分别自然斜坡角等于岩层倾角和自然斜坡角小于岩层倾角(图2)。

同理，根据岩体的极限平衡状态，得到块体的下滑力等于抗滑力:

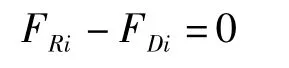
即可算出边坡失稳的横向极限长度。具体的推导可参见相关文献［16］。确定了滑动长度之后便可推导出相应的滑动范围和滑动面，进而可以进行下一步的支挡结构设计和分析。

2.3 滑移弯曲破坏

当岩层倾角满足顺层清方条件时，即岩层倾角等于或大于边坡倾角。一般将优先采取顺层清方，这样不会从坡脚切断岩层。但是当倾角较大，边坡较高，而且岩层薄，有软弱夹层时，边坡中部便有可能弯曲，这样不仅给坡脚的构筑物带来较大的反力，而且，边坡也有可能发生溃曲或弯折破坏。所以，在这类边坡的滑动面确定时，着重考虑的是边坡所在的岩体是否能发生弯曲破坏。

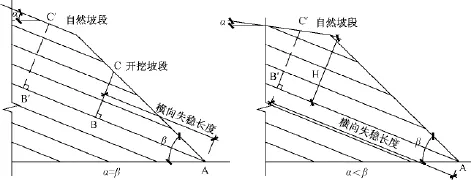
图2 滑移拉裂计算模型Fig．2 The calculation model of sliding fracturing

在前人的研究中［12-13］，许多的学者运用了压杆理论对这类边坡破坏进行了分析。其思路主要是将顺层岩质边坡简化成多层的板梁，利用能量法计算顺层边坡发生溃曲的临界长度来对其进行稳定性分析。这方面，孙广忠等推导出以下计算公式:

李树森等［14］运用能量平衡的原理也推出了相应的临界长度lci判别式:

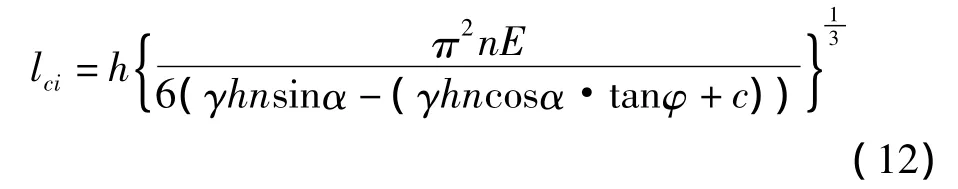
表达式中的符号意义同前。

冯君等［15］还用弹塑性板理论进行了弯曲失稳的临界长度分析。在岩体超过弹性极限之后，便进入了塑形状态，不再满足线性关系。因此可将此时的岩层看成是弹塑性材料。同时，考虑到边坡走向方向长度有限，根据受压理论和能量法，可将边坡岩层视为长度有限的弹塑性板，对顺层岩质边坡的滑移进行研究。

通过假设和推导，得出了边坡的弯曲段岩板边长的极限平衡方程:

用数值软件解出a值便可求得边坡的弯曲段和滑动段的长度，继而确定了滑动面所在的位置，为边坡的加固提供直接理论支撑。

2.4 滑劈破坏

在与滑移弯曲破坏相似的情况下，在临空岩体中有一条软弱节理贯穿岩层面，并将软弱层面的上段部分分割成“犁头”形状。因为上部滑体的滑动而对下部滑体有一个劈裂的作用，将下部岩层剥离出边坡体，最终形成破坏(图3)。

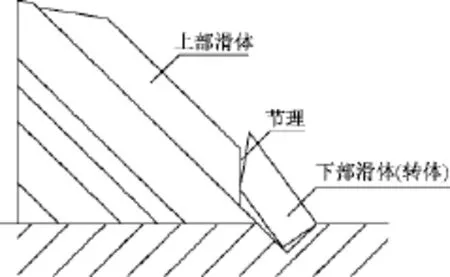
图3 劈裂破坏示意图Fig．3 Diagram of splitting failure

由于坡体破裂的过程中，塑形变形可以忽略不计，因此，将上下两块滑体看成是刚体来考虑。对下部的转体建立力矩平衡方程，即可求出相应的两滑体间的力，进而可求得滑体的安全系数Fs，具体的计算推导可参见相应的文献资料［12］。将求出的安全系数经过判断比较，便可得出滑动面存在的合理性与否。

2.5 楔体破坏

在开挖边坡时，若边坡走向没有与其一致的岩层面，或其夹角不足以形成顺层边坡，但是岩层的倾角是朝向临空面的，应考虑边坡是否形成楔体，并对边坡采取加固措施［16-17］。

由于楔体破坏时，由节理面切割的不稳定滑体将在克服了抗滑力的情况下会沿组合交线或是节理面滑动。因此，可以分别求得在两种情况下的稳定系数和极限坡高。将求出的数值同工程情况相比较，可以得出边坡在不同节理面组合下的稳定情况，并判断最不利的组合方式，作为接下来的边坡设计依据。

宋新龙等［18-19］认为岩质边坡的楔体滑动破坏分为定位楔体破坏及随机楔体破坏两种。定位楔体破坏的滑动面主要由大规模的，明显的断层或是起控制性的结构面构成的。它在坡面上具有一定的连续性和出露位置。确定这类楔体的结构面之后便可用极限平衡法等进行分析。而随机楔体破坏主要是指因为不能充分揭示地质情况，而对楔体形成的节理及结构面不能准确判断。对于这种情况，宋新龙提出一种随机楔体可靠性理论。即在对岩质边坡楔体边界作出正确判断的基础之上，通过分析节理及结构面的分布规律，把Monte Carlo模拟引入到随机楔体的稳定性分析中，通过随机抽取边坡节理裂隙样本，从统计学上来分析边坡的破坏概率及可靠性指标。

3 结语

确定顺层岩质边坡的滑动面是进行边坡稳定性分析的前提。在不同的破坏类型中有不同的确定方法。本文对顺层滑动、滑移拉裂、滑移弯曲、滑劈破坏、楔体破坏的边坡滑动面确定进行了分析研究，对工程实践有借鉴意义。

(1)在顺层滑动中，利用机动位移法或极限平衡法选出最不利滑面。

(2)滑移拉裂破坏中，通过计算岩体的横向失稳长度后可计算相应的滑动范围和滑动面。

(3)滑移弯曲破坏中，利用压杆理论或弹塑性板理论确定弯曲段和滑动段的长度。

(4)滑劈破坏中，将滑体视为刚体，建立力矩平衡方程求出滑块间的力，推导出安全系数。

(5)楔体破坏中，求出不同楔体分别沿组合交线和节理面滑动时的极限坡高，便可得出最不利的组合方式。

［1］方玉树.建筑边坡岩体分类及其应用合理性研究［J］.中国地质灾害与防治学报，2011，22(4):89-96.FANG Yushu.Research on rationality of classification of rock masses for the building slope engineering and its application［J］.The Chinese Journal of Geological Hazard and Control，2011，22(4):89-96.

［2］冯君，周德培，李安洪.顺层岩质边坡开挖稳定性研究［J］.岩石力学与工程学报，2005，24(9):1474-1478.FENG Jun，ZHOU Depei，LI Anhong.Research on stability of rock bedded slopes［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(9):1474-1478.

［3］张倬元，王士天，王兰生.工程地质分析原理［M］.北京:地质出版社，1994.ZHANG Zhuoyuan， WANG Shitian， WANG Lansheng.Principle of engineering geology［M］.Beijing:Geological Publishing House，1994.

［4］殷跃平，彭轩明.三峡库区千将坪滑坡失稳探讨［J］.水文地质工程地质，2007，1(3):51-55.YIN Yueping，PENG Xuanming.Failure mechanism On Qianjiangping landslide in The Three Gorges Reservoir Region［J］.Hydrogeology ＆ Engineering Geology，2007，1(3):51-55.

［5］冯君，周德培，杨涛.水力作用下顺层岩质边坡稳定性分析［J］.岩土力学，2010，31(11):3594-3598.FENG Jun，ZHOU Depei，YANG Tao.Analysis of stability of rock bedded slope under hydraulic pressure［J］.Rock and Soil Mechanics，2010，31(11):3594-3598.

［6］路为，白冰，陈从新.岩质顺层边坡的平面滑移破坏机制分析［J］.岩土力学，2011，32(S2):204-207.LU Wei，BAI Bing，CHEN Congxin.Analysis of mechanism of plane sliding failure for bedded rock slopes［J］.Rock and Soil Mechanics，2011，32(S2):204-207.

［7］曹兴松，赵其华，周德培，等.机动位移法在顺层岩质边坡稳定性分析中的应用［J］.山地学报，2009，27(2):223-229.CAO Xingsong，ZHAO Qihua，ZHOU Depei，et al.A application research of mobile displacement method in parallel rock slope stability analysis［J］.Journal of Mountain Science，2009，27(2):223-229.

［8］王根龙，伍法权，张茂省.平面滑动型岩质边坡稳定性极限分析上限法［J］.工程地质学报，2011，19(2):176-180.WANG Genlong，WU Faquan，ZHANG Maosheng.Method of upper bound limit analysis for plane sliding of rock slopes［J］.工程地质学报，2011，19(2):176-180.

［9］李安洪，周德培，冯君.顺层岩质路堑边坡破坏模式及设计对策［J］.岩石力学与工程学报，2009，28(S1):2915-2921.LI Anhong，ZHOU Depei，FENG Jun.Failure modes of bedding rock cutting slope and design countermeasures［J］. Chinese JournalofRock Mechanics and Engineering，2009，28(S1):2915-2921.

［10］冯君，周德培，江南，等.顺层岩质边坡顺层滑动岩体范围分析［J］.山地学报，2007，25(3):376-380.FENG Jun，ZHOU Depei，JIANG Nan，et al.On the extent of bedding slipping rockmass of consequent rock slope［J］.Journal of Mountain Science，2007，25(3):376-380.

［11］冯君，周德培，李安洪.顺层岩质边坡开挖松弛区试验研究［J］.岩石力学与工程学报，2005，24(5):840-845.FENG Jun， ZHOU Depei， LI Anhong.Physical modeling research on relaxation region of consequent rock slope induced by road cutting［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(5):840-845.

［12］刘钧.顺层边坡弯曲破坏的力学分析［J］.工程地质学报，1997，5(4):335-340.LIU Jun.Mechanical analysis of bend failure of anaclinal slope［J］.Journal of Engineering Geology，1997，5(4):335-340.

［13］刘小丽，周德培.用弹性板理论分析顺层岩质边坡的失稳［J］.岩土力学，2002，23(2):162-165.LIU Xiaoli，ZHOU Depei.Stability analysis of layered dip rocky slopes with elastic plane theory ［J］.Rock and Soil Mechanics，2002，23(2):162-165.

［14］李树森，任光明，左三胜.层状结构岩体顺层斜坡失稳机理的力学分析［J］.地质灾害与环境保护，1995，1(2):24-29.LIShusen， REN Guangming， ZUO Sansheng.Mechanicalanalysis ofinstability mechanism of consequent slope in bedded rockmass［J］.Journal of Geological Hazards and Environment Preservation，1995，1(2):24-29.

［15］冯君，周德培，杨涛.用弹塑性板理论分析顺层边坡的弯曲失稳［J］.岩体工程学报，2010，32(8):1184-1188.FENG Jun， ZHOU Depei， YANG Tao.Stability analysis of consequent rock slopes using elastic-plastic plate theory［J］.Chinese Journal of Geotechnical Engineering，2010，32(8):1184-1188.

［16］房定旺，许传华，毛权生.岩石边坡的滑劈破坏［J］.岩土工程学报，2003，25(6):688-691.FANG Dingwang，XU Chuanhua，MAO Quansheng.Slipsplit failure of rock slope［J］.Chinese Journal of Geotechnical Engineering，2003，25(6):688-691.

［17］宋敏，付厚利，王耿，等.逆倾岩质边加固技术研究［J］.地下空间与工程学报，2011，7(S2):1758-1763.SONG Min，FU Houli，WANG Gen，et al.Study of reinforcing techniques for anti-dip layered rock slopes［J］.Chinese Journal of Underground Space and Engineering，2011，7(S2):1758-1763.

［18］宋新龙，王宇，汪灿.岩质边坡随机楔体稳定性分析的 Monte-Carlo模拟［J］.安全与环境工程，2012，19(1):112-116.SONG Xinlong，WANG Yu，WANG Can.Random wedge block stability analysis with monte carlo simulation for rock slope ［J］. Safety and Environmental Engineering，2012，19(1):112-116.

［19］王宇，宋新龙，张行，等.边坡工程模糊随机可靠度分析［J］.长江科学院院报，2011，28(9):30-34.WANG Yu，SONG Xinlong，ZHANG Hang，et al.Fuzzy stochastic reliability analysis of slope engineering［J］.Journal of Yangtze River Scientific Research Institute，2011，28(9):30-34.