数理逻辑的程序可靠性验证
2015-03-07顾名宇
顾名宇
安顺职业技术学院信息工程系,贵州安顺561000
数理逻辑的程序可靠性验证
顾名宇
安顺职业技术学院信息工程系,贵州安顺561000
摘要:程序可靠性验证往往占用软件开发周期很长的时间,而现行的软件可靠性验证方法主要是基于形式化的方法如基于SPIN的模型检测方法等,但这种方法可能由于模型建立的问题导致验证的复杂性极大提高,造成最后验证失败的结果比比皆是。为解决此问题,本文使用数学方法从数理逻辑角度用推理的方法实现了程序可靠性验证,并完成了客户服务器程序的可靠性验证,证明了该方法切实有效。
关键词:数理逻辑;程序;可靠性
在计算机系统中,软硬件都有可靠性指标的要求并必须经过验证。对于软件设计者来说,如果软件没有通过验证,那么整个系统的可靠性仍是没有保证的。软件可靠性验证方法多种多样,比如有基于SPIN模型检测方法及各种形式分化分析方法等[2][6],很多方法停留在抽象的理论研究上,而在实际应用中很少使用到。
而对于大多数程序员来说,对于程序的可靠性的验证采用了比较熟悉的软件工程的方法,比如软件工程中的白盒、黑盒等测试,但这些测试的统计故障率不能完全作为可靠性评估的依据。例如,即使白盒测试的语句覆盖率达100%,分支覆盖率为90%以上,程序路径覆盖率为70%以上,只能说明这些语句的分支、程序路径没有错误,不能保证程序已达到了很高的可靠性。因为毕竟只覆盖了一部份,也许在未覆盖的部分仍存在着故障率很高的缺陷。
所以,本文结合软件开发实践,探索了一种切实可用的方法,即用基于数学方法的数理逻辑法实现程序可靠性的逻辑推理验证。
1 数理逻辑
数理逻辑又称符号逻辑[5],是用数学方法研究逻辑或形式逻辑的学科。早在1847年,英国数学家布尔建立了一系列的运算法则,利用代数的方法研究逻辑问题,初步奠定了数理逻辑的基础。之后,德国数学家弗雷格让数理逻辑的符号系统更加完备,使现代数理逻辑最基本的理论基础逐步形成,并成为一门独立的学科。
数理逻辑包括两个最基本的也是最重要的“命题演算”和“谓词演算”。
1.1命题演算
命题演算是研究关于命题如何通过一些逻辑连接词构成更复杂的命题以及逻辑推理的方法。命题是指具有具体意义的又能判断它是真还是假的句子。如果把命题看作运算的对象,如同代数中的数字、字母或代数式,而把逻辑连接词看作运算符号,就象代数中的“加、减、乘、除”那样,那么由简单命题组成复合命题的过程,就可以当作逻辑运算的过程,也就是命题的演算。比如:如果x==0, 则y=5;

1.2谓词演算
谓词演算也叫做命题函数演算。在谓词演算里,把命题的内部结构分析成具有主词和谓词的逻辑形式,由命题函数项、逻辑连接词和量词构成命题,然后推导命题之间的逻辑关系。命题函数项就是指除了含有常项以外还含有变项的逻辑公式。常项是指一些确定的对象或者确定的属性和关系,变项是指一定范围内的任何一个,这个范围叫做变项的变域。命题函数项和命题演算不同,它无所谓真和假。如果以一定的对象概念代替变项,那么命题函数项就成为真的或假的命题。例如,如果x==0,则y=5,使用谓词演算来描述,用P(x,y)表示x==y,Q(x,y)表示x=y,x是整数,y是整数,则可描述为P(x,0)->Q(y,5)。
用数理逻辑推理实现程序可靠性验证,主要是把命题演算和谓词演算结合起来,使用相应的推导公式完成目标推理的验证过程。
2 使用数理逻辑验证程序可靠性方法
2.1程序可靠性定义
程序可靠性定义有多种,为方便证明,先看当前的标准的程序可靠性定义:美国IEEE计算机学会对“软件可靠性”作出了明确定义,此后该定义被美国标准化研究所接受为国家标准,多年后,我国也接受该定义为国家标准。该定义包括两方面的含义:
(1)在规定的条件下,在规定的时间内,软件不引起系统失效的概率;
(2)在规定的时间周期内,在所述条件下程序执行所要求的功能的能力。
2.2程序可靠性验证步骤
这里的验证排除了软件开发阶段的各种错误,主要考虑系统失效和程序功能问题。使用数理逻辑验证程序的步骤可分为以下三步:
(1)根据程序需求建立模型[5],对所要验证的程序或模块进行抽象化[3],构建检测模型。
从程序可靠性定义得知,主要涉及到到程序系统失效和功能问题。
程序的失效主要涉及数据输入和函数调用问题,建立如下数学描述:x1,x2,x3,…,xn是n个变量或输入数据,用V(xi)(0<=i<=n)表示xi取值合法,用F1,F2,…Fm表示函数调用,因参数数量各不相同,故参数略,用P1,P2,…PK表示函数的参数调用,S表示程序正常。
用y1,y2,…yl表示要完成的功能项,W(yj)表示完成的第yj个功能,其中0<=j<=l,
(2)使用逻辑公式表示所要验证的性质,公式要能正确地表达所要验证的内容。
为便于描述验证性质,规定:
=F1()˅F2()˅…˅Fn()
=F1()˄F2()…˄Fn()
程序的失效主要是通过合法和非法数据获取或录入,调用规定的函数及参数实现结果S,当满足规定的条件时,下面公式为真:
->S
其中0<=l<=n,0<=t<=n。
从一名大学毕业生到田园创客,从农资店长到合作社理事长,又从农场经理到“正阳牛”打药团队队长,牛超凭着一股“牛劲儿”和 “牛脾气”,扎根田园,不懈努力,带领“正阳牛”团队自主研发农机植保设备,与广西田园植保公司联盟,在正阳成立“正阳牛”民兵植保服务队136个,分别与全县60多家农机合作社、60家家庭农场、60家种粮大户签订了农药统防统治和庄稼植保托管合同,植保面积达100万亩,每年劳务收入近300万元。牛超被当地农民称赞为追梦田园创业的“植保达人”和“正阳牛人”。
对于程序功能正确性证明,当满足程序规定的条件时,可以描述为:
->T
T表示“真”,->T为真,说明程序功能都正确。
(3)验证,通过对输入值或变量设置合法和非法的数据,程序能正常结束,且所有变量在所有函数路径中取值都符合要求[1],每条语句所包括的所有变量的取值都满足相互的逻辑关系,能完成规定的功能,即说明程序是可靠的。
在数理逻辑证明以上公式过程中,所有命题公式和谓词演算的推理理论都实用。如果程序较为复杂,可按其定义的函数或把其分解为多个函数后用相应可能的参数代入来进行测试,确保每个都是真即得到S。
同理可以完成的证明。
3 用数理逻辑法验证客户服务器程序
在客户端服务器程序设计中,常常有客户端向服务器提交一系列任务(R1..Rn),该序列任务是具有某个呼叫计划标志。而服务端将该呼叫任务标志添加到R1……Rn呼叫队列中,该队列是一维数组R_Work[Max],Max是提交任务最大量。往该数组添加计划呼叫标志的条件是数组R_Work[i].bz=0 (0<=i < Max)。客户端每次向服务端提交任务请求,服务端必须从该客户端呼叫队列提取任务,并完成相应的执行任务。
客户端向R_Work[Max]添加任务采用如下程序F1:

提交任务

服务端检测某个客户端的提交任务采用如下的方式:
程序F2:

程序完成相应的任务
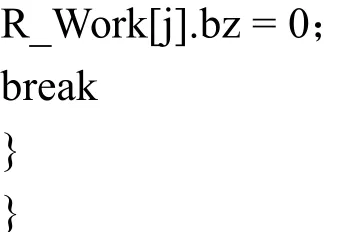
这里涉及到两个函数F1和F2,函数F1可提交1-MAX个任务,F2可以执行相应的任务,由程序可靠性验证可以进一步抽象出:对于任意的任务i,当满足R_Work[i].bz=0时,有F1(i),0<=i 再来看看程序可靠性第二方面的证明,即程序功能性证明: 设:提交第i个任务简写为F1(i),执行第j个任务简写成F2(j) 从前面看出存在: 当R_Work[i].bz=0时,F1(i)为真 当R_Work[j].bz !=0是,F2(j)为真 当i 实际上,通过阅读程序F1、程序F2,很容易就可以发现在F2很有可能先处理后添加进来的任务,而前面添加的任务得不到执行。 所以必须修改代码程序F1、F2,使其按照时间顺序执行任务。如果在R_Work[i]中增加一个时间成员,那么每次检测队列即数组时要对R_Work进行排序,使用最快的算法也要增加Max*log(Max)次运算。 所以考虑对每个任务,添加了一个R_Nextwork变量(初始为0),对程序F1、F2做了如下的修改: 对修改过的程序,除了增加几个变量外[4],程序代码和F1、F2区别不大,所以程序可靠性第一方面证明没有问题,下面进一步证明程序可靠性的第二方面,即功能性证明: 现在建立模型: 有任务R1,….,Rn,存在任意Ri、Rk,Ri F3(Ri)->T,F3(Rk)->T,F4(Rk)->T为重言式 证明目标:证明F4(Ri)先于F4(Rk)执行,即F4(Ri)->T也成立。 现在来分析: (1)对于程序F3,因为有:F3(Ri)->T,F3(Rk)->T,且Ri (2)对于程序F4,因为F4(Rk)->T成立,所以F4(Rk)被执行。同时,对于任意Ri,存在R_Nextpoll=Ri;对于数组下标k,k=(R_Nextpoll+ i)%Max,如果i> 0,有Rk后于Ri被处理。Rk为数组k下标对应的时间序任务。 综合(1)(2),得出:当Ri和Rk都被提交后,只要F4(Rk)->T成立,那么F4(Ri)->T也成立,并在F4(Rk)之前执行。 在程序的可靠性验证中,程序验证的复杂性在于执行流程、时间和环境的不确定性使验证的内容与目标的关系难以把握,如果采用适当的验证方法,将会极大减少程序的测试和验证时间,特别是随着程序复杂性越来越高,采用单一的验证方法满足不了程序可靠性的要求。本文研究了采用数理逻辑的方法实现程序的可靠性验证,数理逻辑对程序的可靠性验证需要根据程序构建验证模型,然后根据条件,推导出相应的结果是否符合要求。数理逻辑方法可以不拘泥于形式,如果在其基础上把数学工具中的方法综合运用将会起到事半功倍的效果,也为广大软件开发人员及测试人员快速实现程序验证提供了一种新的尝试。 参考文献 [1]万良.基于隔离逻辑的并行程序可靠性验证方法[J].计算机工程,2014,40(2):86-91,96 [2]李兴锋,张新常,杨美红,等.基于SPIN的模块化模型检测方法研究[J].电子与信息学报,2011,33(4):902-907 [3] Alexey G, Honseok Y. Modular Verification of Preemptive OSKernels[J].ACM SIGPLAN Notices,2011,46(9):404-417 [4] Cohen E, Schulte W, Tobies S. Local Verification of Global Invariants in Concurrent Programs[C]//Proceedings of the 22nd international conference on Computer Aided Verification.Berlin:Springer 2010:480-494 [5]黄达明,曾庆凯.基于分离逻辑的程序验证技术[J].软件学报,2009,20(8):2051-2061 [6]单卓为,鱼滨.基于SPIN的CSCW系统的验证[J].计算机技术与发展,2008,18(4):9-12,15 [7] 0’Heam P W. Tutorial on Separation Logic[C]//Proeeedings of the 20th International Conference on Computer Aided Verification.Berlin: Springer, 2008:15-21 Validation of Reliability on Mathematical Logic Program GU Ming-yu Anshun Vocational and Technical College of Information Engineering, Anshun 561000, China Abstract:The reliability verification of program often takes a very long time to develope the software, while the current software reliability verification method is mainly based on formal methods such as SPIN based on model checking method, but this method may lead to the complexity of verification to improve greatly bing due to model problems, and then finally fails in validation results everywhere. In order to solve this problem, this paper used mathematical methods from mathematical logic perspective to realize the program reliability verification, and completed the reliability verification of client server program, the method was be proved the validity in true. Keywords:Mathematical logic; program; validation 作者简介:顾名宇(1960-),男,贵州安顺人,副教授.研究方向:项目管理,信息安全. E-mail:gumingyu60@126.com 收稿日期:2013-07-13修回日期: 2013-07-24 中图法分类号:TP301 文献标识码:A 文章编号:1000-2324(2015)04-0621-04

4 小结
