基于集对分析的河流水质综合指数评价模型

高苏蒂， 方达宪， 潘争伟

（1.安徽新华学院 土木与环境工程学院，安徽 合肥 230031；2.合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

目前，有关水质综合评价方法的研究已有很多［1－5］，常用的方法是将水质监测数据取平均值从确定性角度对水环境质量进行评价，因其忽略了水质信息因各种主客观因素带来的不确定性，所以难以准确反映水体水质的真实状态。河流水环境系统是一个具有模糊性、不精确性特征的大系统，受到污染的水域其污染物浓度分布都呈现出一定的随机性和不确定性，而数量有限的监测数据或监测点位，使得人们对待评的水域水环境质量状态不可避免地存在主观认识上的模糊不确定性。近年来，陆续有人尝试将模糊理论技术用于表征系统或事物的随机性、模糊性，比如盲数模型评价法、三角模糊数法、联系数法、集对分析法等，其中大部分在水质评价方法中的应用也取得了较好的效果［6－11］。本文尝试将模糊逻辑理论与集对分析理论耦合，用于水质综合指数评价方法研究，应用构建的六元“同异反层次法”联系数，结合集对分析理论的同一性、差异性和对立性，建立水质综合指数评价的集对分析模型，根据该模型，不仅可以利用某河段水质资料计算出属性识别的水质等级识别结果，还可以得出其综合评价结果对各等级的隶属度。

1 集对分析基本理论

集对分析（set pair analysis，SPA）是中国理论学家赵克勤在1989年提出的一种系统理论和方法，用联系数处理事件系统中的模糊随机性、不确定性，基本思想是对客观存在的不确定性给予承认，把被研究的客观事物之确定性联系与不确定性联系在同一性、差异性和对立性等3方面进行辩证分析和数学处理［12］。

1.1 联系数的基本理论

集对是集对分析理论的基础，由一定联系的2个集合组成，在涉及的具体问题之下，通过分析集对的同一性、差异性和对立性，建立集对的联系数表达式，从而描述事物之间的确定性与不确定性，联系数的基本表达式一般记为：

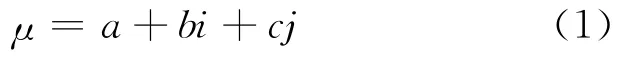
其中，a、b、c分别表示集对的同一度、差异度和对立度，取值区间［0，1］，且a＋b＋c＝1；i表示差异度系数，i∈［－1，1］，有时只起差异标记的作用；j表示对立度系数，取定值为－1，有时只起对立标记的作用。

（1）式仅对描述对象所处的状态空间作“一分为三”的划分，称为同异反联系数或三元联系数，是建立在对描述对象作“同、异、反”划分基础上的，在许多实际应用中，稍显粗糙尚不够细化［10］，为此，需对联系数的基本表达式μ＝a＋bi＋cj作不同层次的扩展，其中“bi”和“cj”项扩展后形成一种多元联系数［7－13］，其表达式可为：

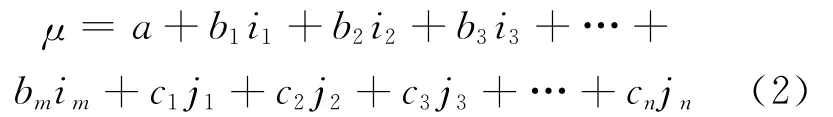
当m＝3，n＝2时，即称为集对分析六元联系数：

其中，a、b1、b2、b3、c1、c2为联系分量，a，b1，b2，b3，c1，c2∈［0，1］，a＋b1＋b2＋b3＋c1＋c2＝1；i1、i2、i3为差异度系数，i1，i2，i3∈［－1，1］，有时只起差异标记的作用；j1、j2为对立度系数，j1、j2取定值为－1，有时只起对立标记的作用。

1.2 六元“同异反层次法”联系数

根据集对分析理论，对（2）式进一步作同异反划分，建立集对图，如图1所示。

第1层关系为传统的同异反关系，第2层关系是对上一层关系的细化，差异性可因其偏同性、偏反性进一步划分为偏同差异、偏反差异和中差异，对立性可根据其偏异性进一步划分为偏异对立和对立，从而解决度量规则粒度过大的问题［12－13］。

对（3）式中的各分量进一步作“同异反”划分，如将“偏同差异b1i1”按一定比例分配给“同一a”“偏同差异b1i1”和“中差异b2i2”，则可建立六元“同异反层次法”联系数表达式（4）式。

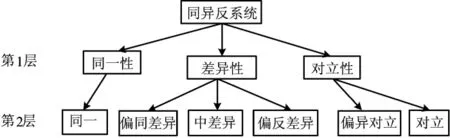
图1 同异反层次结构

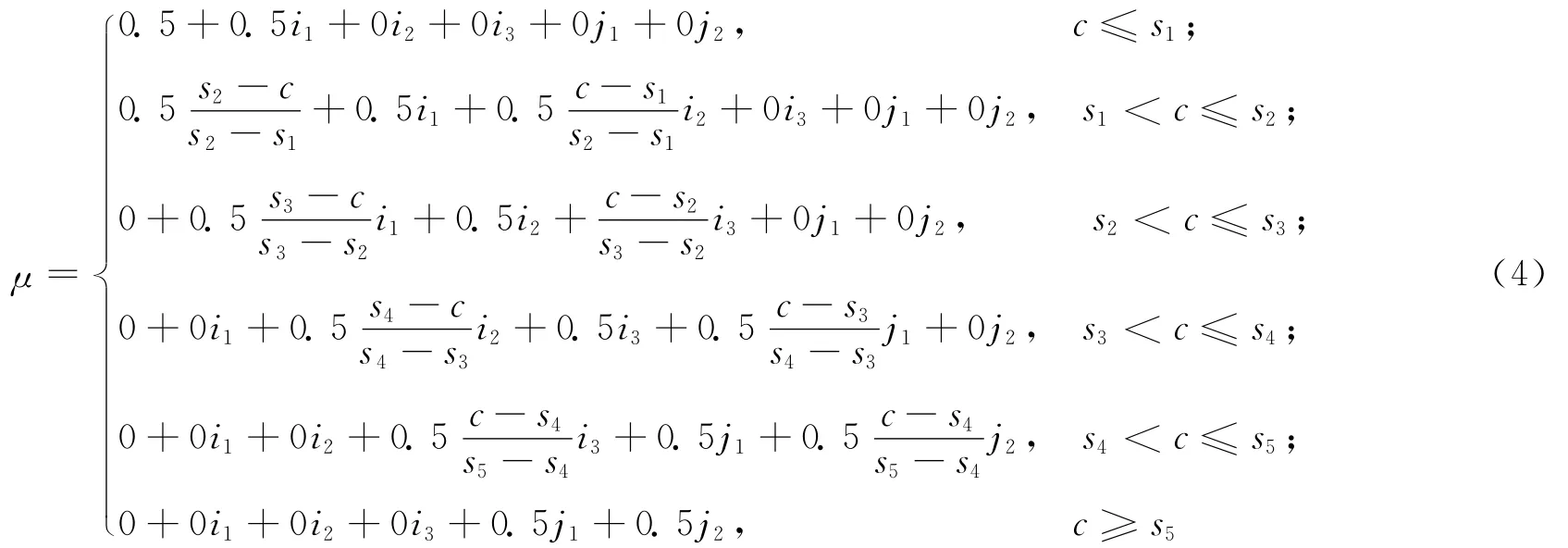
其中，c为评价指标的样本值；sk（k＝1，2，…，5）为 第k级评价指标的标准临界值。

1.3 基于集对分析理论的水质评价模型

应用构建的六元“同异反层次法”联系数，可建立一般河流水质评价的集对分析模型。假设从河流中选取15个具有代表性的采样点，设第r个采样点的评价指标样本值组成评价指标集Ar＝［c1，c2，c3，c4］（r＝1，2，3，…，15），水质评价标准为5个等级，各等级的评价标准临界值组成标准集Bk（k＝1，2，3，…，5），则集合Ar、Bk可构成集对H＝（Ar，Bk）。由（4）式可得出各采样点的评价指标联系数，则可构建出联系数矩阵μrk，根据指标权重向量Wk和联系数矩阵，采用加法加权综合法［14－15］对各采样点进行水质综合评价，即得：

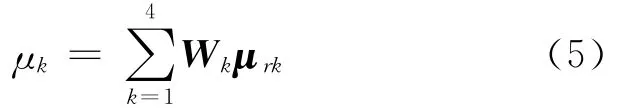
由（5）式即可得出各采样点的水质等级识别结果，在此不妨将这个含有集对分析理论的评价模型称为基于集对分析的水质评价模型。

2 实例应用

为评价某河流水质状况，可从该河流某河段选取15个具有代表性的采样点进行取样分析，分析五日生化需氧量（BOD5）、高锰酸钾盐指数（CODMn）、氨氮（NH3－N）和溶解氧（DO）4项常规评价指标（在实际应用中，也可以根据具体情况选择其他一些指标进行评价），所得数据见表1所列（D为氧亏，因溶解氧DO质量浓度与其他3个指标数据对评价结果产生的影响相反［2］，为统一起见，以氧亏D代替溶解氧质量浓度，假定饱和溶解氧质量浓度为8.33mg／L）。

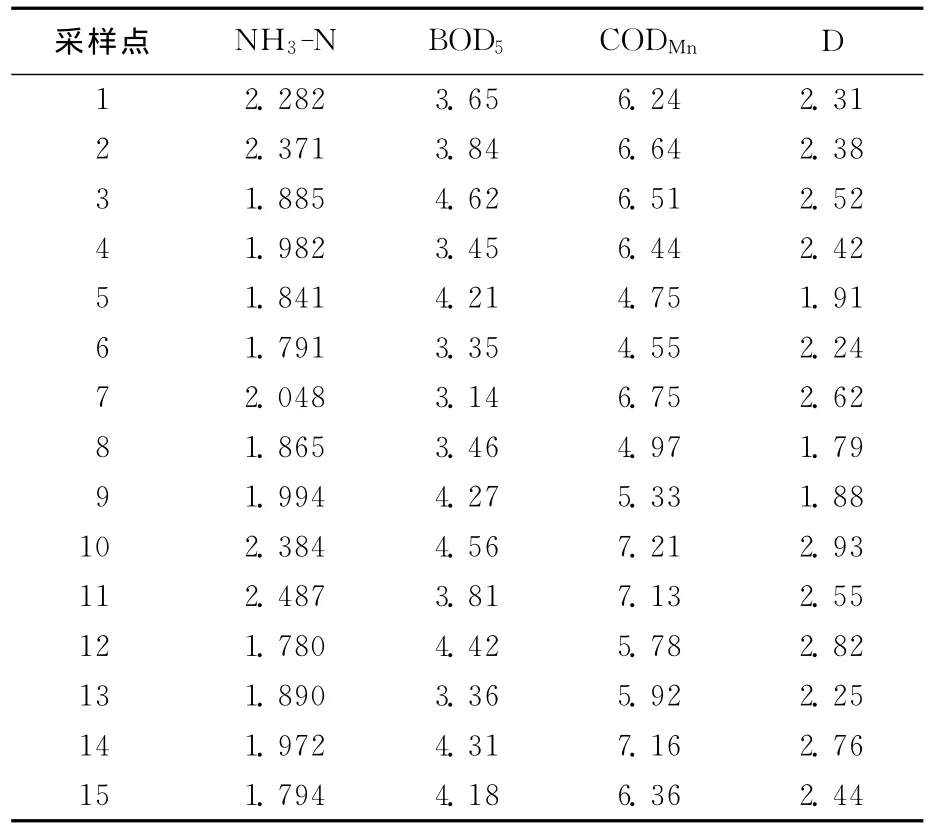
表1 采样点所得4项指标的监测数据 mg／L

应用构建的六元“同异反层次法”联系数，通过建立的一般河流水质评价的集对分析模型，经过如下计算过程即可得到水质评价结果。

（1）构建研究对象集对。设第r个采样点的评价指标样本值组成评价指标集Ar＝ ［c1，c2，c3，c4］（r＝1，2，3，…，15），各等级的评价标准临界值组成标准集Bk（k＝1，2，3，…，5），则集合Ar、Bk可构成集对H＝ （Ar，Bk）。

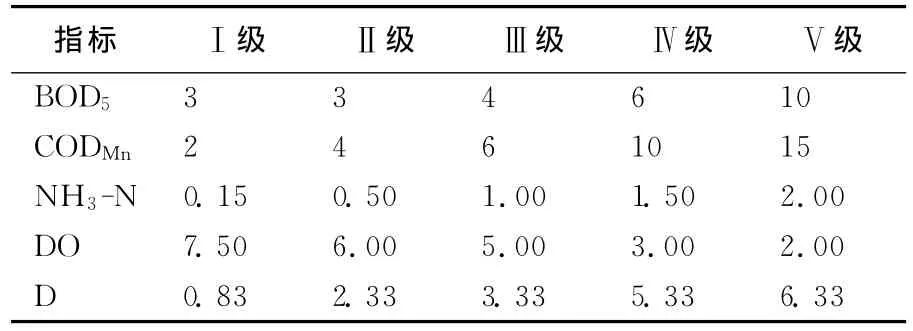
表2 水环境质量等级标准 mg／L

（2）确定六元“同异反层次法”联系数，构建联系数矩阵。现以采样点1为例，由（4）式得各评价指标的联系数计算公式，将选取的15个具有代表性的采样点遵循此种方法得出各采样点评价指标联系数，则可构建出联系数矩阵。4项评价指标的联系数公式如下：

对于D，有

对于BOD5，有

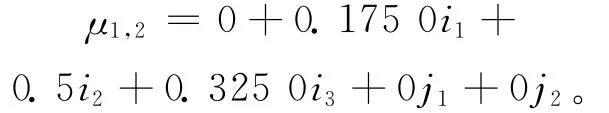
对于CODMn，有

对于 NH3－N，有

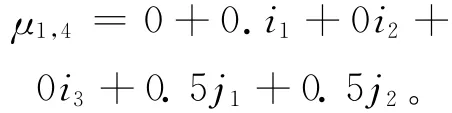
（3）确定评价指标权重。这里综合专家意见［17］确定4项评价指标 D、BOD5、CODMn、NH3－N权重向量集W＝［0.28，0.28，0.20，0.24］。

（4）综合评价分析。首先对采样点进行水质综合评价。采用加法加权综合法［14－15］对各采样点进行水质综合评价，根据指标权重向量集W和联系数矩阵，由（5）式即可得出各采样点的水质等级识别结果，见表3所列。

然后采用平均联系数对各指标进行水质综合评价，即

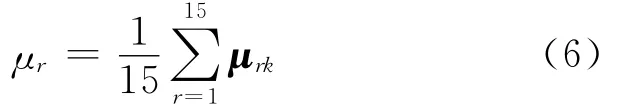
由（6）式即可得出各指标的水质等级识别结果，见表4所列。

由上可知，利用耦合了模糊理论与集对分析计算方法的水质评价模型，可计算出一般河流某河段属性识别的水质等级识别结果及综合评价结果对各等级的隶属度。

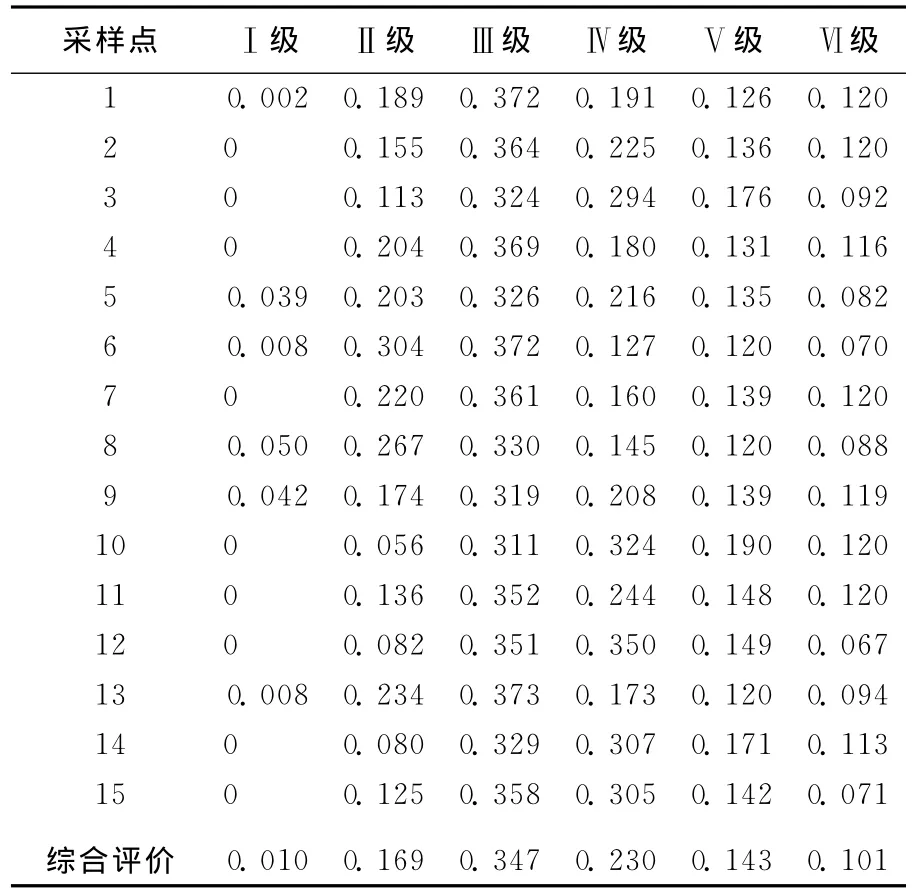
表3 各采样点水质等级识别结果

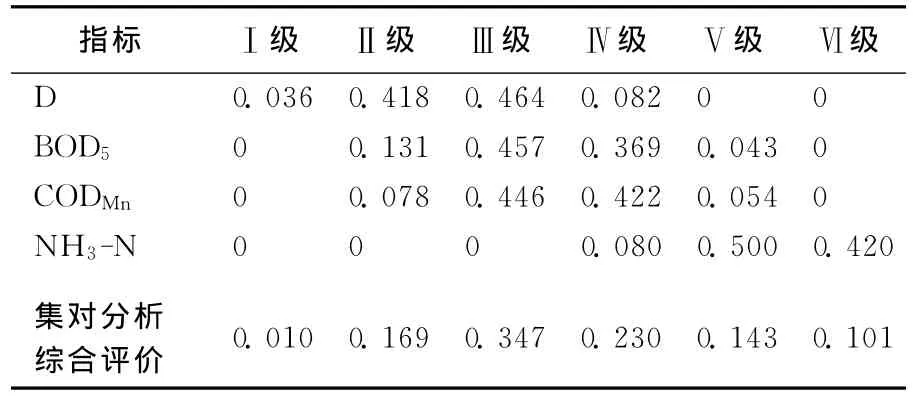
表4 基于集对分析的各指标水质等级识别结果

为验证基于集对分析计算方法的水质评价模型的正确性、适用性及可操作性，用模糊综合评价法［17］对该河流水质进行综合评价计算，所得结果见表5所列。

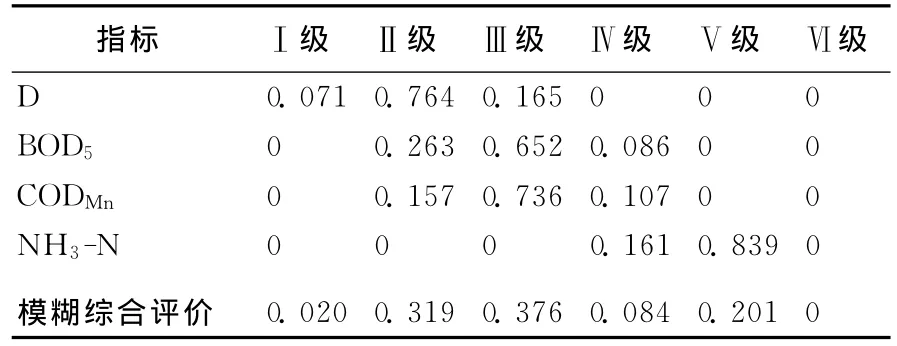
表5 采用模糊综合评价法所得各指标水质等级识别结果

3 讨论分析

由2种方法的计算结果不难发现，利用耦合了模糊理论与集对分析计算方法的水质评价模型，从采样点和评价指标2个方面分析得出，该河段水质综合评价结果偏重于Ⅲ、Ⅳ级，属于Ⅲ级的隶属度为0.347，属于IV级的隶属度为0.230，其他级别所占比例较小，所以可以综合判断该河流水质为Ⅲ级。从模糊综合评价法分析计算的结果可以看出该河段水质综合评价结果偏重于Ⅱ、Ⅲ级，属于Ⅱ级的隶属度为0.319，属于Ⅲ级的隶属度为0.376，其他级别所占比例较小，Ⅵ级计算结果为0，因而该等级识别结果数据可以省略不计，其他各指标水质等级识别结果不受影响，所以可以综合判断该河流水质为Ⅲ级。文献［18］的结果也与这2种方法得出的河流水质状态相近。经过与多种计算方法所得出的结果比较发现，基于集对分析法的水质评价计算模型是正确的、可信的。

因而基于水环境系统随机性、灰性和未确知性等多种不确定，将模糊逻辑理论与集对分析理论耦合，结合集对分析理论的同一性、差异性和对立性，应用构建的六元“同异反层次法”联系数，建立水质评价的集对分析模型，与以往一些方法相比，利用该模型不仅可计算出一般河流某河段属性识别的水质等级识别结果，还可以得出其综合评价结果对各等级的隶属度，这种模型计算方法更加精确、可信，能够准确地刻画水环境质量状态，并且在实际应用中，也可以根据具体情况选择其他一些特定指标进行评价。

4 结束语

河流水环境系统是一个复杂的不确定性系统，系统内的水质状态同时受多种因素的影响和作用，已有数据往往忽略了水质信息因各种主客观因素带来的不确定性，因而难以准确反映水体水质的真实状态。本文从水环境系统的模糊性、不精确性出发，将模糊逻辑理论与集对分析理论耦合，建立水质评价的集对分析模型，利用该模型计算出一般河流某河段属性识别的水质等级识别结果及综合评价结果对各等级的隶属度，实例研究证明，基于集对分析理论的水质评价模型分析计算所得的综合评价结果精确、可信，符合实际，从而为准确刻画水体水质的真实情况提供了一个思路，在水环境管理和保护领域具有一定意义。

［1］ 陈丽燕，付 强，魏丽丽.五元联系数在湖泊水质综合评价中的应用［J］.环境科学研究，2008，21（3）：82－86.

［2］ 李如忠.基于盲数的水质综合指数评价模型［J］.中国农村水利水电，2008，19（6）：19－22.

［3］ 陈东景，马安青，徐中民，等.因子分析法在水质评价中的应用［J］.水文，2002，22（3）：29－31.

［4］ 顾文权，邵东国，黄显峰.模糊多目标水质管理模型求解及实验验证［J］.中国环境科学，2008，28（3）：284－288.

［5］ 沈时兴，金菊良，宋松柏，等.水文水资源集对分析的理论基础探讨［J］.合肥工业大学学报：自然科学版，2013，36（12）：1481－1488.

［6］ 李如忠.水质综合评价灰关联模型的建立与应用［J］.安徽建筑工业学院学报：自然科学版，2002，10（1）：46－49.

［7］ Silvert W.Ecological impact classification with fuzzy sets［J］.Ecological Modelling，1997，96（2）：1－10.

［8］ Ronald E G，Robert E Y.Analysis of the error in the standard approximation used for multiplication of triangular and trapezoidal fuzzy numbers and the development of a new approximation ［J］.Fuzzy Sets and Systems，1997，91（1）：1－13.

［9］ Ronald E G，Robert E Y.A parametric representation of fuzzy numbers and their arithmetic operators［J］.Fuzzy Sets and Systems，1997，91（2）：185－202.

［10］ 吴开亚，金菊良，潘争伟.基于三角模糊数截集的城市洪涝易损性联系数评价模型［J］.水利学报，2010，41（6）：711－719.

［11］ 赵吴静，吴开亚，金菊良.防洪工程安全评价集对分析可变模糊集模型［J］.水电能源科学，2007，25（2）：5－7，13.

［12］ 赵克勤.集对分析及其初步应用［M］.杭州：浙江科学技术出版社，2000：9－43.

［13］ 赵克勤.SPA的同异反系统理论在人工智能研究中的应用［J］.智能系统学报，2007，2（5）：20－35.

［14］ 金菊良，魏一鸣.复杂系统广义智能评价方法与应用［M］.北京：科学出版社，2008：1－150.

［15］ 于国荣，叶 辉，夏自强，等.投影寻踪分类模型的改进及在水质评价中的应用［J］.四川大学学报：工程科学版，2008，40（6）：24－29.

［16］ GB 3838－2002，国家地表水环境质量标准［S］.

［17］ 郭素萍，陈国栋.模糊综合评价在太子河辽阳段水质评价中的应用［J］.东北水利水电，2008，26（2）：50－52.

［18］ 高苏蒂.河流水质评价与环境容量计算方法的改进及应用［D］.合肥：合肥工业大学，2007.