LD 0.5型全液压矿运车直线行走工况联合仿真研究

刘 相， 柳 波

（1.中南大学 机电工程学院，湖南 长沙 410012；2.徐工集团江苏徐州工程机械研究院，江苏 徐州 221000）

0 引 言

LD 0.5型全液压矿石转运车集成了电机车头和矿运车的功能，自带动力，适用于隧洞装运，矿山、水利等工程的施工及中小断面引水洞、矿山转运工程，主要用于空间狭窄的洞采作业，包括磷矿、铁矿、铜矿、金矿、银矿、铅锌矿巷道等各种中小矿山。

对于井下行走机械而言，轮胎是其与路面接触的唯一部件，轮胎－地面的相互作用对整车运动状态有决定性作用；车辆操纵稳定性、行驶安全性、制动性能、通过性、动力学性能等都与轮胎力学有直接关系［1－3］；在进行车辆系统结构和零部件优化时，都离不开轮胎力学分析。大部分机电系统，机械结构和控制系统之间都会形成强耦合闭环，单独对任一个系统分析都很难准确描述耦合闭环的影响。因此，机液联合仿真有着较重要的工程意义和实用价值［4］。轮胎地面接触模型较为复杂，结合AMESim的液压仿真优势和ADAMS的动力学仿真优势能够对矿运车直线行驶工况进行详细分析，完整再现其实际运行情况［5］。

1 LD 0.5型矿用运输车结构概述

矿运车车架为焊接箱型结构，行走轮和驱动马达与车体螺栓相连，其中左、右2个马达安装在支撑板的中间，采用四驱形式，四行走轮位于支撑板的两端，马达与行走轮通过双齿轮链条带动行走轮系运动，同侧车轮始终具有相同的转速。同时，通过对马达的控制实现整机的前进、后退、转向等动作。通过操作液控手柄动作，实现矿运车整机运动。

行走系统采用单泵双马达，辅以压力补偿手动换向阀的形式，流向马达的流量根据手动比例来调节大小，通过控制使供给马达流量不同，实现矿运车速度调节。

新能源矿运车的三维结构如图1所示。

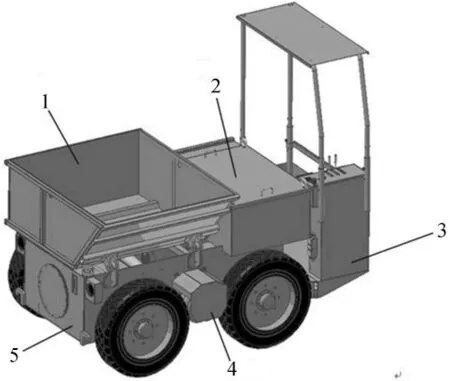
图1 矿运车三维结构图

2 轮胎－地面力学数学模型分析

由于矿运车工作于路面条件较差的井下，为了提高作业可靠性，采用实心轮胎，在计算分析时可认为轮胎是刚性的。

图2所示为车轮的计算简图，z代表车轮与土壤相互作用时的沉陷量。

车轮与土壤之间会产生相互挤压，假设土壤单位作用面积上的反力为p，取一个长度为dS、宽度为b位于轮胎外缘上的微小面积，其反作用力为：

车轮受到的径向载荷W与车轮受到的土壤反力相互平衡，即

轮轴上受到的水平推动力引起的车轮水平方向的反作用力为：

图2 车轮与地面相互作用时的计算简图

根据文献［6－7］提出的汽车地面力学计算模型，土壤支撑面积上的压力p和沉陷量之间的数值关系如下：

其中，K为土壤变形模量；n为土壤变形因子；p为车轮平均单位压力；z为车轮沉陷量。

将（3）式代入（1）式，可得：

根据图2所示的几何关系，结合相似三角形原理，则有：

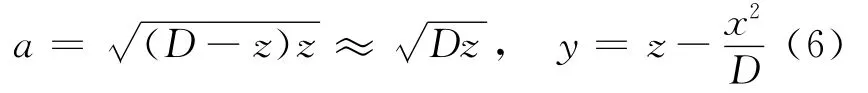
将（6）式代入（5）式，可得：

其中，将（z－x2／D）n展开成zn－nzn－1（x2／D）＋…，并忽略高阶项的影响，可得：

将承压模型（4）式代入（3）式，可得：

由（4）式反解z，可得：

将（9）式代入（8）式，最终得到车轮滚动阻力的表达式为：

3 联合仿真模型建立

将矿运车的Inventor三维模型导入ADAMS，并定义各部件的约束、材料属性，根据实际工况轮胎选用Fiala模型，它是建立在弹性基础上的梁模型，能够满足一般的分析需要［8］。调整好路面和轮胎参数后，得到的ADAMS动力学模型如图3所示。由于重点分析矿运车转向过程，因此对原先的三维模型进行了简化［9］，只考虑整机质量、质心位置以及轮距、轴距、轮胎外形尺寸等关键参数。

图3 矿运车ADAMS模型

为了完成ADAMS和AMESim之间的联合仿真，需要设置信息交换变量，并定义数据通讯接口。AMESim输出左、右马达的转矩给ADAMS模型，ADAMS模型传回车轮转速给AMESim，采用continuous模式在AMESim中完成计算。定义AMESim的输出变量为zuo－conrol－torque（左马达输入扭矩）、you－conrol－torque（右马达输入扭矩）；运用ADAMS里的 Measure函数测出两侧车轮转速，通过Control Plant模块将转速值导入AMESim：zuo－omega（左马达输出转速）、you－omega（右马达输出转速）。

AMESim和ADAMS的联合仿真模式有2种，即continuous模式和discrete模式，前者适用于小型机械系统，后者多用于大型复杂机械系统仿真，本文选取continuous模式。设置联合仿真步长为0.005s，ADAMS输出步长为0.01s，将前述建立好的接口模块导入AMESim软件，最终得到的联合仿真模型如图4所示。

图4 矿运车行走系统机液联合仿真模型

4 仿真结果分析

矿运车的斗容约为0.53m3，根据相关资料，铁矿石的松散密度约为1.2～1.8t／m3，此处取1.6t／m3，计算得矿运车载质量约为830kg；液压马达排量为234mL／r；溢流阀调定压力为25MPa。换向阀得电，并在1s内阀口达到最大开度；在第35.5s，换向阀失电，用以模拟矿运车直线行走时的制动性能，仿真时间设定为40s。仿真结果中，力、位移、速度等矢量若为正值，代表与仿真系统设置的坐标方向相同。

4.1 运动学仿真结果

矿运车质心的位移曲线如图5所示。其中图5a为X方向的位移曲线，矿运车在40s内前进了约40m；图5b是Y和Z方向的位移，单位mm，矿运车在Z方向的位移基本为0，这说明矿运车在直线过程中基本没有侧向偏移，矿运车Y方向位移在第14s出现了2个正值尖峰，这是由于矿运车在该时间遇到了凸起障碍，前轮和后轮在过障碍时车体在Y方向上均会产生位移；在第30s出现2个负值尖峰，矿运车在该时间遇到凹陷沟壑。正常的直线行驶时间矿运车质心Y向位移稳定在130.6mm。另外，可看出矿运车在启动初始阶段，质心在Y方向有一定的偏移，最大数值达到了10mm，这是因为车体刚启动时在惯性力作用下产生了小幅抖动。

图5 矿运车质心的位移曲线

车体质心速度、加速度曲线如图6所示。

由图6a可知，在匀速行驶阶段矿运车行驶速度为1.13m／s，与设计时速4km／h较为接近。在矿运车刚遇到障碍物时，速度有一定下降，经历短时间的波动后恢复正常。矿运车刚遇到障碍时，负载压力突然增大，换向阀两端压差减小，压力补偿器来不及调节，导致流量减小。在车体经过沟壑时，初始阶段速度略有增加，这是在重力分力作用下的短时间加速。在第35.5s，换向阀掉电，在39.6s车体速度降为0，制动时间约4s，制动距离为2m。

由图6b可知，在启动阶段，加速度最大值达到0.37m／s2，制动阶段最大值达到0.65m／s2，在矿运车经过障碍物和越过沟壑时车体加速度均有一定波动。

图6 车体质心速度、加速度曲线

矿运车轮胎纵向打滑率、滚动半径和侧偏角的变化曲线如图7所示。

由图7a可知，在启动时，轮胎纵向打滑率最大为13.8%，制动时最大达到23.6%，刚遇到障碍物的一瞬间打滑率达到了26%。对比矿运车质心加速度曲线可知，轮胎的纵向打滑率与加速度变化趋势相同，加速度越大轮胎打滑越严重，在车辆满载情况下，不宜采用过大的启动和制动加速度，否则会加快轮胎磨损。

由图7b可知，在启动过程中，轮胎半径有较为明显的减小趋势，最小达到326mm；在匀速行驶阶段，轮胎滚动半径稳定在331mm；在制动阶段，轮胎滚动半径最大达到335.4mm；在越障和过沟壑时，轮胎滚动半径出现了波动。在驱动力和制动力的作用下，轮胎会产生不同程度的滑移和滑转，导致其有效滚动半径发生变化。在越障和过沟壑时，轮胎受到冲击载荷，加之轮胎本身是弹性体，在外界载荷和弹性回正力的共同作用下导致其滚动半径发生了波动。

由图7c可知，整个行进过程中，在启动、制动、越障过沟壑以及匀速行驶阶段，矿运车轮胎的侧偏角基本为0。这说明矿运车在直线行驶时轮胎受到的侧向力很小，几乎没有发生侧偏。

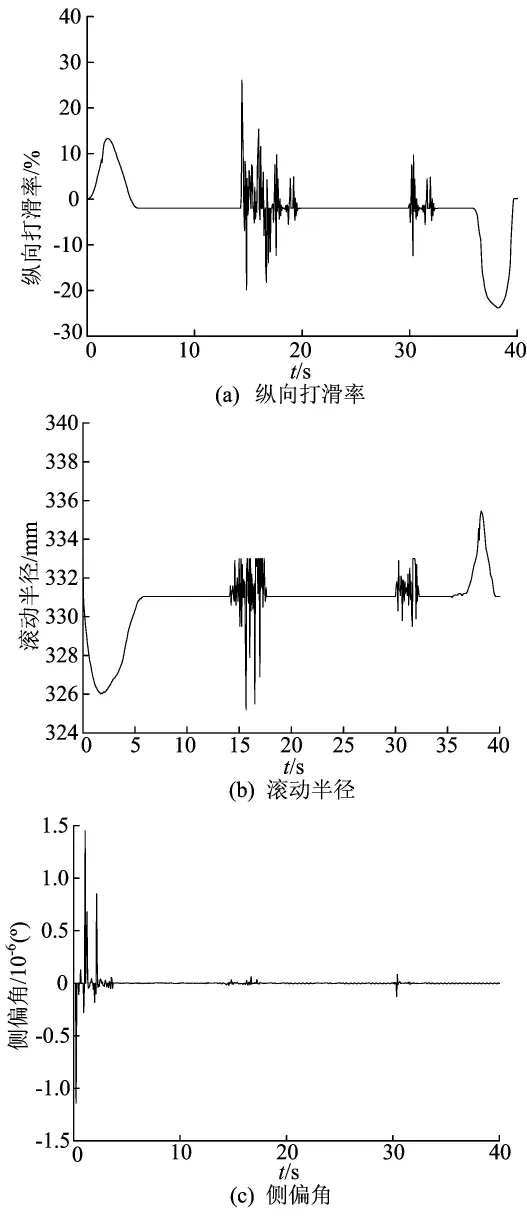
图7 矿运车轮胎纵向打滑率、滚动半径和侧偏角的变化曲线

4.2 动力学仿真结果

矿运车的机械结构较为简单，且采用了比较宽裕的安全系数，关于矿运车的动力学分析以轮胎－地面负载为主。

矿运车轮胎纵向、径向受力如图8所示。

由图8a可知，启动时轮胎最大纵向力达到1 270N，方向是沿着车体行进方向；制动时纵向力峰值为1 321N，与车体行进方向相反；稳定行驶阶段车轮纵向力为360N。在车体越障过沟壑时，轮胎纵向力出现了一定程度的波动，可发现车体纵向力的变化趋势与纵向打滑率一致。

图8 矿运车轮胎纵向、径向受力

由图8b可知，轮胎径向受力启动时最大值为6 575N，制动时最小值为5 280N，匀速行驶时稳定在6 138N，四轮径向总受力基本与矿运车总重力相等。结合图7b轮胎的滚动半径变化曲线可知，轮胎启动时，有效滚动半径减小，轮胎受到径向挤压，因此造成轮胎径向力会比匀速行驶时偏大；车体制动时，轮胎滚动半径会有略微增大，产生回弹，导致径向力减小。车体遇到障碍时，可以看到径向力出现了较大波动，最大峰值达到12 160N。这与实际情况是吻合的，车辆行进间突遇凸起障碍物时，最直接受到影响的就是车轮径向力。为了尽量简化结构，矿运车轮系组件省去了悬挂减震系统，而采用了类似滑移装载机的刚性连接轮系结构，因此一定程度上会承受较大的冲击载荷。从仿真可以看出，在设计轮系结构时，必须采取较大的安全系数，或者采用屈服强度更大的优质钢材，以弥补缺少悬挂减震的弊端。

车轮行进时的滚动阻力矩变化曲线如图9所示，其变化规律和轮胎径向力基本一致，启动时最大值达115N·m，制动时最小值为83N·m，稳定行驶时为104N·m，越障碍时滚动阻力矩峰值达到230N·m。

图9 矿运车轮胎滚动阻力矩

4.3 液压系统工作压力

矿运车液压行走系统可通过单向阀保压，该项功能在实际中有着重要意义。矿运车到达装料点后，进行装料作业，该过程持续时间40～60s，此时为了节省电量，可先关闭电动机。借助单向阀作用，系统在短时间内实现保压［10］，完成装料后重新开机，马达工作压力不会从0瞬间增大，减小了对液压马达、管路产生的液压冲击。

液压系统工作压力曲线如图10所示。矿运车直线行走工作压力为5.2MPa，在遇到凸起障碍物时，压力出现了一定超调，最大值达到8.3MPa；在过沟壑时，轮胎负载突然减小，马达工作压力短时间内出现下降，最小值为2.9MPa，经过短暂调整后恢复正常。在过障越沟壑时，压力补偿器起到了较好的调节作用。

图10 矿运车直线行走液压系统工作压力

5 实验验证

虽然仿真分析能够在很大程度上反应系统动态性能，但由于仿真模型的简化和建模中的相关假设，还需要进一步通过现场实验来验证仿真建模、分析的正确性［11］。本文设计了矿运车行驶性能的测试实验方案，并将实验结果与仿真分析结果进行对比分析。LD 0.5型矿运车实验样机图如图11所示。

图11 LD 0.5型矿运车实验样机

5.1 实验设备

现场需要的实验设备包括CEM华盛昌AT－8手持非接触式转速表、上海众野多功能便携式液压测试仪以及压力传感器、转速计等。矿运车的各作业状态通过PC端实验面板界面读取，如图12所示，该界面能够清楚看到矿运车的各项工作参数。PC端软件可将测得的数据转换为EXCEL或者TXT格式文本，结合其他绘图软件，为仿真－实验对比分析提供便利。

图12 矿运车PC端实验面板

5.2 测试结果分析

由于实验场地条件有限，实验时将分别单独模拟矿运车过凸起障碍以及矿运车过沟壑时的情况。模拟过障碍的方法是在路面上铺设木桩，并在木桩两端加固定设施，防止矿运车过障时，木桩发生偏移。模拟过沟壑的方法是操作矿运车通过下水道沟渠。实验结果如图13所示。

对比图10的系统压力仿真曲线可知，整个过程压力变化的趋势基本相同，但是实验中的压力数值比仿真结果大，而且在稳定行驶过程中还是会有小幅度波动。这是因为仿真中使用的路面谱是理想化的平整地面，实验时的水泥路面难免会有一定的起伏，因此造成了压力波动。在矿运车过障碍和过沟壑时，相比于仿真结果，系统压力出现了更加明显的超调，经过调整后压力恢复正常。整体而言，仿真结果比较贴近实际工况。

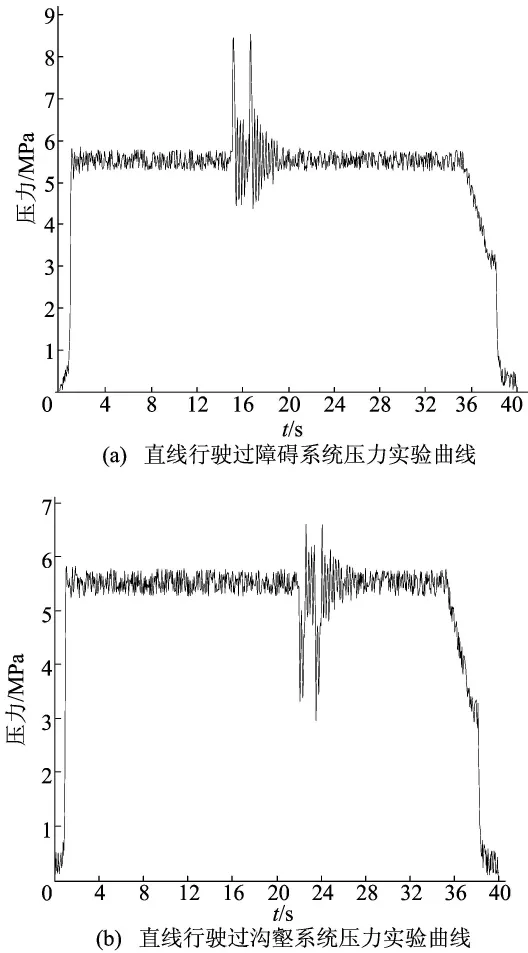
图13 矿运车实验液压系统压力曲线

6 结 论

（1）根据Bekker地面力学理论建立了轮胎－地面负载模型，为仿真分析奠定了基础。

（2）利用ADAMS动力学软件和AMESim液压仿真软件建立了矿运车直线行走工况的联合仿真模型，详细分析了矿运车直线行驶过程中的动力学、运动学特性。

（3）开展矿运车实验样机的现场测试实验，实验结果表明矿运车的直线行驶性能基本达到设计要求，且仿真结果与实验结果基本吻合，证明了仿真建模的正确性。

［1］ 郭孔辉.汽车操纵动力学原理［M］.南京：江苏科学技术出版社，2011：112－118.

［2］ Maurice J P，Berzeri M，Pacejka H B.Pragmatic tyre model for short wavelength side slip variations［J］.Vehicle System Dynamics，1999，31（2）：65－94.

［3］ Pacejka H B，Besselink I.Magic formula tyre model with transient properties［J］.Vehicle System Dynamics，1997，27（1）：234－249.

［4］ Sun Ying，He Ping，Zhang Yunqing，et al.Modeling and co－simulation of hydraulic power steering system［C］／／International Conference on Measuring Technology and Mechatronics Automation.IEEE，2011：595－600.

［5］ Fang Zhigang，Guo Xuexun，Xu Guanneng.Modeling and simulation of hydraulic power steering system［C］／／International Conference on Electric Information and Control Engineering.IEEE，2011：2343－2345.

［6］ 庄继德.计算汽车地面力学［M］.北京：机械工业出版社，2001：30－40.

［7］ 陈晋市.滑移装载机行走系统研究［D］.长春：吉林大学，2012.

［8］ Cabrea J A，Ortiz A，Carabias E，et a1.An alternative method to determine the magic tyre model parameters using genetic algorithms［J］.Vehicle System Dynamics，2004，41（2）：109－127.

［9］ 胡 朋，潘晓东，侯超群.考虑路堤影响的车辆侧滑与侧翻临界风速［J］.合肥工业大学学报：自然科学版，2012，35（11）：1523－1527.

［10］ 陈 英.工程机械液压系统保压设计及改进［J］.煤矿机械，2010，31（9）：160－162.

［11］ 赵 锋.装载机全液压转向系统机液联合仿真与实验研究［D］.长春：吉林大学，2012.