基于永磁操动机构的同步合闸时间预测方法研究

马晶晶， 肖本贤

（合肥工业大学 电气与自动化工程学院，安徽 合肥 230009）

0 引 言

电力网是一个动态系统，供需变化与功率平衡问题要求电网各部分能够可靠、及时地投入或切除。而电网中的电力负荷如电动机、变压器等大部分都是感性负荷，在运行过程中需向这些设备提供无功功率，通过一定的无功补偿可以提高电网的功率因数，从而降低输配电设备的容量需求、减少线路损耗、稳定电网电压等。在我国，广泛采用并联电容器组来实现电压控制和无功补偿。但无功补偿电容器组控制装置随机投切电容器组时，可能会产生暂态过电压、涌流和低压侧过电压升高，这些开关的暂态过程会对系统设备造成危害，影响电网稳定［1－3］。近年来，同步开关技术得到应用，该技术能够有效地抑制暂态过电压和过电流，减少绝缘损坏，提高电力系统供电质量，降低电力装置的误动作［4－5］。

本文选用陪永磁机构的真空断路器作为同步投切装置的执行器。要使断路器做到同步投切就必须精确地预测其动作时间，否则很难达到预期效果。永磁机构的动作时间主要受控制电压、环境温度、机构老化和触头磨损等因素的影响，这些因素的影响非常复杂，因此研究实用的预测方法来提高其预测精度是很有必要的。

目前已发表的文献中，主要采用的方法有多元线性回归法［5］、加权平均算法［6］、神经网络法［7－11］、双 线 性 插 值 法［12］和 电 流 闭 环 控 制 算法［13］。

其中，文献［5］借鉴多因素时间序列的预测方法，将影响永磁机构真空开关的多重因素综合考虑，明确各影响因素的自回归系数，利用多元线性回归法动态预测开关的动作时间与变化趋势，同时对各种影响因素引起的开关操作时间偏差进行补偿和预测，预测值误差小于0.2%，说明设计的模型是适用的。

文献［7］认为径向基神经网络比误差反向传播网络更适合分散性较大的关合时间预测，提出了基于不同温度段、不同预测模型的分布式结构的径向基神经网络，使训练速度、预测精度都有大幅度的提高。

文献［9－11］运用前向神经网络建立了模型，分析了实测控制电压数据、环境温度数据对预测结果的影响，建立了基于BP神经网络的误差带预测，开发了以实测影响因素数据为基础，基于人工神经网络的动作时间预测系统，预测结果能满足同步控制的要求（ABB提出的同步关合时间允许误差为±1ms，关断为±2ms）。

文献［12］基于典型的机械开关动作时间服从正态分布的统计特性，根据统计特性获得控制电压、环境温度对同步断路器动作时间的影响补偿表，由查表和线性插值分别获得控制电压、环境温度对其的补偿值，再采用自适应反馈控制策略对触头磨损和阻尼系数进行动态补偿，计算出动作时间的估计值，测试结果也表明系统的同步关合最大误差为±0.5ms，同步关断最大误差为±1.2ms。

文献［13］根据适当提高驱动电压并使其保持恒定，将有效地降低环境温度对继电器动作时间影响的研究结果，提出了一种利用反馈电流结合PID算法来调整继电器动作时间的方法，经过数万次的现场实验，涌流比保持在2以内，满足同步开关的要求。

目前主要的问题是如何提高永磁机构开关动作时间的预测精度，特别是环境因素不稳定情况下的预测精度。本文将遗传算法（genetic algo－rithm，GA）和粒子群优化（particle swarm optimization，PSO）算法运用于实测控制电压和环境温度的前向神经网络预测模型，用该模型进行预测，并对预测结果进行分析，然后利用公式计算出老化和磨损的补偿时间即可得到较为精确的合闸时间，从而完成对合闸时间的预算，为下一次的精确合闸提供依据。

1 合闸时间的补偿与预测方法

1.1 老化和磨损的补偿时间模型

对于给定的永磁机构，控制电压、环境温度、机械老化与触头磨损等都会对其动作时间带来影响，其中，控制电压和环境温度的影响是主要的。在建立基于前向神经网络的时间预测模型之前，采取反馈控制策略来补偿由机械老化与触头磨损等不确定因素对动作时间的影响，即应用历史数据检测开关操作特性的变化趋势，并预测下一次操作所需的动作时间。为了更好地反映老化和磨损的累积效应，减小偶然因素造成的干扰，通常取前n次操作的结果作加权处理，则有：

其中，Δt（n）为对第n次继电器动作时间的预测误差；ωi为滤波权值；k一般取1.2～1.4。

1.2 环境因素影响的BP神经网络预测模型

动作时间和控制电压、环境温度的关系是一种非线性、复杂的映射关系，很难用数学解析的方法确立模型，因此利用BP网络强大的非线性映射能力和良好的泛化能力，对这一关系进行系统建模。

BP神经网络又称为误差反向传播（back propagation）神经网络，是一种多层的前向型神经网络，由输入层、隐层、输出层组成。应用于动作时间预测的3层BP网络预测模型结构如图1所示。在该预测模型中，输入信号有控制电压和环境温度，输出为动作时间，所以输入层节点数为2，输出层节点数为1，隐含层节点数在训练过程中确定。

下面以继电器关合操作为例，在正常工作条件范围内，选择不同温度、不同控制电压进行关合实验，得到关合时间随它们变化的曲线。从得到的曲线中选取若干点作为样本数据，进行归一化处理。选取不同的隐层数对网络进行训练，考虑到输出的取值范围较大，因此在输出层采用线性神经元，隐含层采用S形神经元，同时为提高网络的收敛速度，采用Levenberg－Marquardt算法对网络进行训练，通过对训练结果的比较，发现隐层数取7较合适，此时均方根误差较小且有较快的收敛速度。

虽然BP神经网络得到广泛应用，但也存在以下不足：训练时间长；易陷入局部极小值；不同的起始点可能导致不同的最优解；在训练过程中学习新样本时有遗忘旧样本的趋势。

图1 BP网络结构

2 遗传算法和粒子群优化算法

2.1 遗传算法

BP神经网络各层的初始权值和阈值很大程度上影响着BP神经网络的预测性能，因此选取合适的网络初始权值和阈值可以提高神经网络的预测能力。因此本文将GA和BP神经网络相结合，利用GA来优化BP神经网络初始的权值和阈值，提高BP神经网络的收敛速度，减小BP算法陷入局部最优的可能性［14］，具体步骤如下：

（1）随机初始化种群。个体编码采用实数编码方式，每个个体均为一个实数串，由输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值构成。

（2）确定适应度函数。以预测输出和实际输出之间的均方差的倒数作为适应度函数F，即

其中，N为网络输入输出样本对的个数；y（k）和（k）分别为网络理想输出与实际输出。

（3）选择操作。从种群中选择若干个体作为双亲用于繁殖后代，采用轮盘赌法进行选择操作，适应度高的个体遗传到下一代的概率较大，而适应度低的个体遗传到下一代的概率则较小。每个个体i被选择的概率pi为：

其中，c为种群个体的数目；Fi为个体i的适应度值。

（4）交叉操作。2个配对的个体按照某种方式以交叉概率pc交换其中部分基因，从而形成2个新的个体。采用实数交叉法，第k1和第k2个个体在第j位基因交叉操作方法如下：

其中，gk1j、gk2j分别为第k1和k2个个体在第j位的基因；r为［0，1］之间的随机数。

（5）变异操作。以一个比较小的变异概率pv选择第i个个体的第j个基因gij进行变异，从而增加种群的多样性，变异操作方法如下：

其中，gmax、gmin分别为基因gij的上界和下界；r1为一个随机数；s为当前迭代次数；smax为最大进化次数；r2为［0，1］间的随机数。

（6）计算适应度函数值。若满足算法结束条件则输出优化的权值和阈值，若不满足算法结束条件则返回步骤（3）。

（7）以GA输出的优化权值和阈值作为BP神经网络的初始权值和阈值，用训练样本对BP神经网络进行训练。

2.2 粒子群优化算法

针对前向神经网络易陷入局部极小值的缺点，PSO算法被引入预测模型中。PSO算法是一种全局优化算法，将其应用到前向神经网络的训练算法中，可以有效弥补基于梯度下降的前向神经网络存在着容易陷入局部最小的缺陷。

在PSO算法中，优化问题的潜在解可被看作是d维搜索空间中的一个粒子。若干随机分布的初始粒子在搜索空间中以一定的速度运动，该速度取决于自身的惯性、最优位置和群体的最优位置，即在一个d维搜索空间中，由m个粒子组成种群x＝ ［x1，x2，…，xm］T，其中第i个粒子的位置为xi＝ ［xi1，xi2，…，xid］T，速度为vi＝ ［vi1，vi2，…，vid］T，第i个粒子的个体最优位置为pi＝［pi1，pi2，…，pid］T，种群的最优位置为gi＝ ［gi1，gi2，…，gid］T。对于粒子i第k维，由第j到j＋1次迭代，其位置和速度的更新规则为：

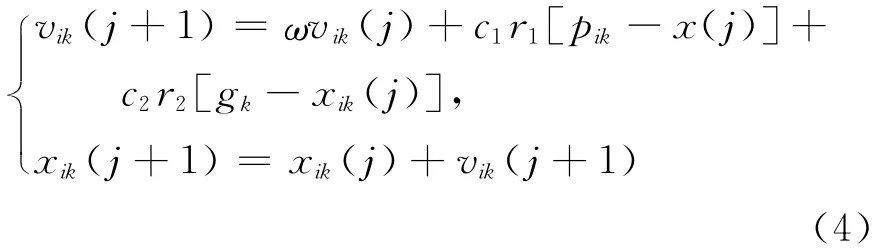
其中，ω为惯性因子；c1和c2为学习因子；r1和r2为［0，1］中的随机数。

惯性因子ω被用于控制粒子的探索能力，学习因子c1和c2用于控制粒子的认知能力和粒子之间的信息共享能力。为了保证粒子具有均衡的搜索能力，必须合理选择惯性因子和学习因子。

PSO算法没有遗传操作，如交叉和变异，而是利用个体在运动解空间中的随机速度来改变个体，其解群相对进化而言，表现出更强的随机性，计算复杂度也比遗传算法低。粒子具有记忆的特性，通过“自我”学习和向“社会”学习，有针对性地从群体中学习有用信息。PSO算法的信息共享机制与GA并不相同。在GA中，染色体互相共享信息，整个种群是比较均匀地向最优区域移动；在PSO算法中，信息流动是单向的，即只有全局最好位置信息将传递给其他的粒子，这使得整个搜索更新过程始终跟随当前最优位置［15］。

PSO算法优化的基本流程如图2所示。

图2 PSO算法优化流程

3 算例与分析

下面以永磁机构合闸操作为例，训练样本数据借鉴文献［16］的实验数据，分别采用基于遗传算法优化神经网络、粒子群优化神经网络和基于前向神经网络的动作时间预测模型，对实际合闸时间进行预测。样本数据如图3所示。

运用BP神经网络模型、GA－BP神经网络模型以及粒子群优化BP神经网络对永磁机构合闸时间进行预测，预测数据点选取温度分别为－13.3、－11.6、－10、－8.3、－7.1、－4.3、3.2、11.1、21.8℃及控制电压在164～168V范围内的合闸时间实验数据80组，其中前40组数据作为训练样本，后40组数据作为测试样本，设置迭代次数为8，并利用20次训练结果的平均误差作为评测依据。

预测结果如图4所示。

图3 样本数据

图4 GA－BP网络、PSO－BP网络与BP网络的预测结果

分别对GA和粒子群算法优化前、后基于前向神经网络模型得到的测试样本进行了记录，将各自的预测结果与实测合闸时间进行比较，并利用平均绝对误差（MAE）、平均绝对百分比误差（MAPE）以及平方和误差（SSE）3个指标对预测效果进行评价，所得误差见表1所列。

表1 GA和PSO算法优化前、后BP网络的预测误差 s

由表1可知，与优化前的前向神经网络预测模型相比，采用遗传算法和粒子群优化后的前向神经网络预测模型的平均绝对误差分别下降了42.1%、37.6%，平均绝对百分比误差分别下降了34.2%、29.6%，平方和误差分别下降了61.0%、56.6%，这表明在断路器合闸时间的预测模型中，遗传算法和粒子群优化后的前向神经网络的预测准确性高于优化前的结果。结合图4可以看出，BP神经网络不同的初始权值和阈值在一定程度上影响着BP神经网络的预测性能。

4 结束语

本文阐述了同步关合技术在抑制系统暂态过电流和过电压的作用，深入研究了同步合闸时间预测的算法及其优化，从而保证相控开关选相操作的精度。

GA和PSO算法优化后的前向神经网络预测模型比优化前的具有更高的预测准确性，预测结果的平均绝对误差、平方和误差和平均绝对百分比误差均较小。

BP神经网络存在初始权值和阈值的随机性，不同的初始权值和阈值很大程度上影响着网络的预测精度。

［1］ 陆 华.配电网并联补偿电容器组操作过电压的研究［D］.杭州：浙江大学，2006.

［2］ 郭丽娟，梁小冰.10kV电容器组切换在用户侧产生的电压放大现象［J］.电网技术，2003，27（2）：21－24.

［3］ Bellei T A，O＇Leary R P，Camm E H.Evaluating capacitorswitching devices for preventing nuisance tripping of adjustable－speed drives due to voltage magnification［J］.IEEE Transactions on Power Delivery，1996，11（3）：1373－1378.

［4］ 丁富华，段雄英，邹积岩.基于同步真空断路器的智能无功补偿装置［J］.中国电机工程学报，2005，25（6）：30－35.

［5］ 丁富华.真空开关的选相控制及其应用研究［D］.大连：大连理工大学，2006.

［6］ Tsutada H，Hirai T，Kohyama H，et al.Development of synchronous switching controller for gas circuit breakers［C］／／Transmission and Distribution Conference and Exhibition：Asia Pacific，Vol 2.IEEE／PES，2002：807－812.

［7］ 赵 佳，吕家锋.基于分布式神经网络的同步合闸时间预测方法研究［J］.上海电气技术，2009，2（1）：36－39.

［8］ 张庆杰，袁海文.配永磁机构的真空断路器同步分合闸控制系统设计与实现［J］.电力自动化设备，2010，30（3）：98－102.

［9］ 谢将剑，李 鹏，崔国荣.基于永磁操动机构的同步关合关键技术的研究［J］.高压电器，2010，46（7）：1－7.

［10］ 汪玉凤，刘芳芳，薛建清.针对矿井电网的机械投切电容器组动态无功补偿控制系统的设计［J］.电网技术，2011，35（8）：218－222.

［11］ 幸晋渝，刘 念，郝江涛，等.基于DSP和人工神经网络的智能同步断路器研究［J］.电力自动化设备，2005，25（1）：21－24.

［12］ 方春恩，周承鸣，邹积岩.同步断路器的统计特性分析及自适应控制［J］.高压电器，2006，42（3）：183－185.

［13］ 仲 浩，胡仁杰.基于电流闭环控制的无功补偿电容器组同步投切装置［J］.电力系统保护与控制，2012，40（6）：129－134.

［14］ 王建平，陈正伟，栾庆磊，等.基于多群体遗传算法的汉字识别系统设计［J］.合肥工业大学学报：自然科学版，2010，33（1）：42－46.

［15］ 倪春波，孔一斐，杨月全，等.粒子群优化及其在多机器人系统中的应用展望［J］.中南大学学报：自然科学版，2013，44（Z2）：126－132.

［16］ 孙明灿，林 莘.无功补偿电容器组的同步投切装置研究［J］.华通技术，2006，25（1）：13－16.