基于双边滤波改进的Harris特征点检测

朱少何， 檀结庆，2

（1.合肥工业大学 计算机与信息学院，安徽 合肥 230009；2.合肥工业大学 数学学院，安徽 合肥 230009）

0 引 言

在图像局部区域中，特征点包含了重要的信息，如目标识别等均是基于特征点。特征点提取的精确度及质量好坏直接影响后续的处理任务，所以图像的特征点检测［1－2］是一项重要的研究内容。在局部区域中，灰度变化最剧烈的点即为特征点，如边界交叉点［3］。

文献［4］利用图像局部梯度信息提出了Harris特征点检测算子，对图像平移旋转和光照变化有很强的稳定性，但存在如下2个问题：①此方法无法保持尺度不变性；②Harris特征点检测算子使用高斯平滑滤波，无法检测一些较弱的特征点。

针对前一个问题，文献［5］提出了多尺度的Harris特征点检测，但出现了特征点的冗余，后与LOG函数结合去除冗余点，效果不是很好；针对后一个问题，文献［6］提出了用双边滤波代替文献［4］中的高斯滤波器，有很好的边缘保持性，但对尺度问题没有很好地解决。

针对Harris特征点检测的不足，本文提出了一种改进的Harris检测方法，用双边核函数替代多尺度Harris中的高斯滤波，在检测特征点的同时进行分组，使同一局部区域的特征点分到同一组，然后利用局部信息选出一个最具有代表的特征点，剔除冗余点。

1 经典算法

1.1 Harris算子

文献［4］提出的Harris算子是一种基于灰度强度变化的点特征提取算子。设f（x，y）为图像函数，Ix、Iy为像素点（x，y）在x、y方向的一阶导数并定义自相关矩阵：

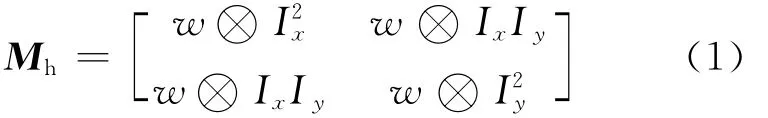
其中，⊗为卷积；w为高斯滤波函数，公式如下：

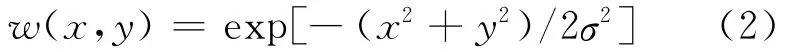
设λ1、λ2为Mh的2个特征值，当λ1、λ2均很大，即认为是Harris特征点。为避免对矩阵Mh进行特征值分解，重新定义了特征点响应函数（即Harris算子）：

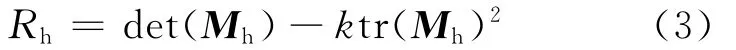
其中，det（Mh）为Mh的行列式；tr（Mh）为Mh的迹；k为经验值，一般取0.04～0.06。当像素点（x，y）的Rh值为局部最大时，就是特征点。由矩阵理论易证明Harris算子对图像平移、旋转及光照变化具有很好的稳定性。

1.2 Harris－Laplace算子

1.2.1 尺度空间理论

文献［7］提出的尺度空间理论是指用尺度变化的核函数对原图像进行卷积，来获得多尺度空间图像的表示序列，表示如下：

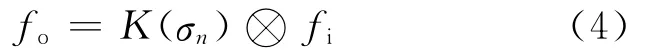
其中，fi为输入图像；⊗为卷积；K（σn）为尺度空间核函数；fo为输出图像。文献［7－8］证明了高斯函数是唯一的尺度空间函数。二维高斯函数定义为：

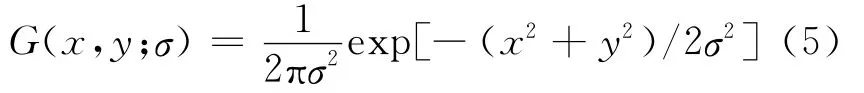
1.2.2 Harris－Laplace算子

为使Harris算子有尺度不变性，将尺度空间理论应用到Harris特征点检测上，得到多尺度的Harris自相关矩阵为：

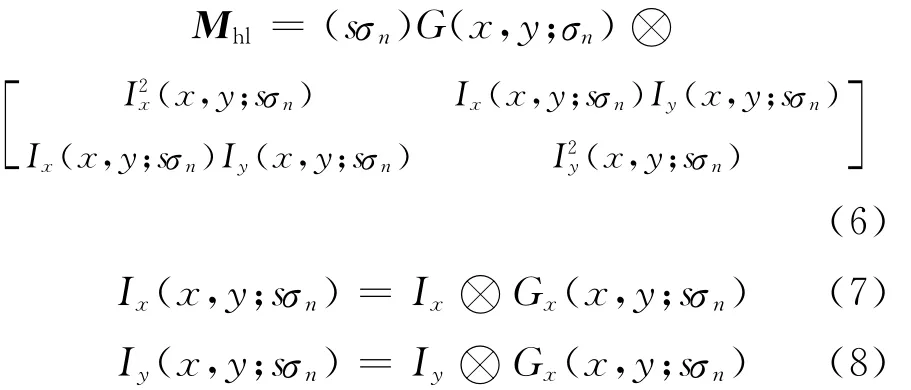
算法如下：

（1）利用（9）式寻找多尺度Harris特征点作为最终特征点的候选点。

（2）在候选点中找能使（10）式在局部尺度中取得极大值的点作为最终的特征点。

实验结果也说明多尺度Harris算子和Harris－Laplace算法有很多的冗余，Harris－Laplace算法不能很好地去除冗余点及剔除较弱的特征点，如图1、图2所示。

其中，Ix、Iy分别为图像f（x，y）在x和y方向的偏导；sσn为微分尺度，σn＝ξn－1σ1；Gi（x，y；sσn）为高斯函数G（x，y；sσn）在i方向上的微分。由此（3）式就变成了多尺度Harris算子，即

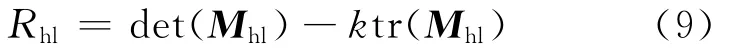
由于多尺度Harris特征点检测时没有重复剔除的机制，（9）式出现了大量的冗余点。文献［5］用LOG函数来去除冗余点，这就是Harris－Laplace方法。LOG算子［9］定义如下：

图1 多尺度Harris特征点检测结果

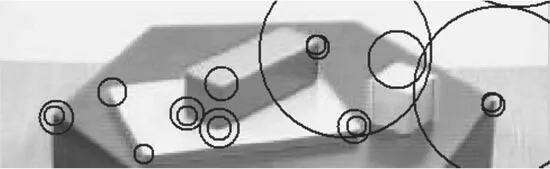
图2 Harris－Laplace方法检测结果

2 双边滤波器的应用

双边滤波［10］是一种非线性的平滑滤波，表达式如下［11］：

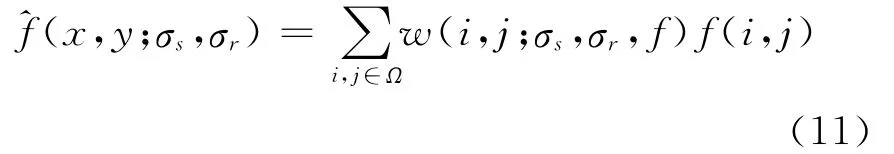
其中

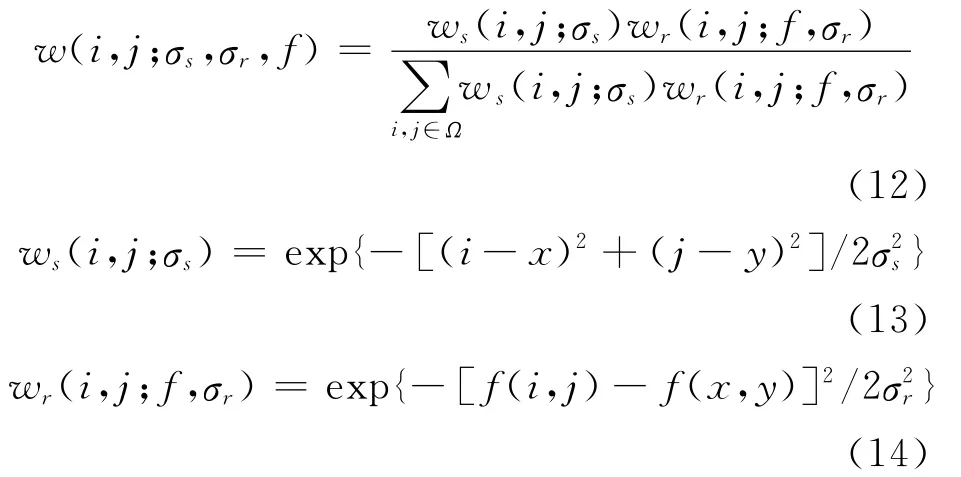
（12）～（14）式都是采用指数运算，其硬件运算慢。文献［12］介绍连分式在数字图像处理中的若干研究中指出了对指数函数的逼近，有理函数逼近比线性多项式逼近更优，文献［13－15］对连分式的理论及应用进行了详细的介绍。

文献［12］也给出了关于函数ex的Thiele连分式的展开式：

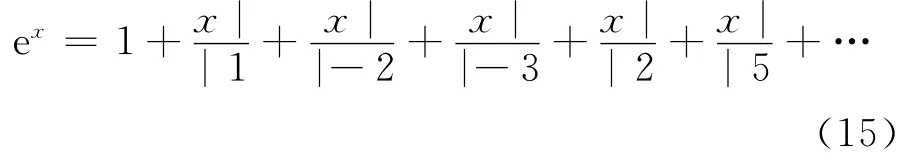
对（15）式的前3项渐近分式如下：

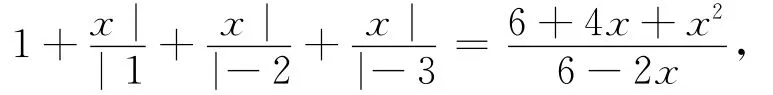
由此可得：

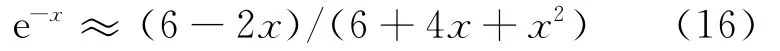
将（13）式、（14）式用（16）式进行逼近计算，然后计算（12）式，形成改进的双边滤波，减少硬件计算量。

将（11）式滤波函数带入（1）式，则可以得到双边滤波的自相关矩阵：

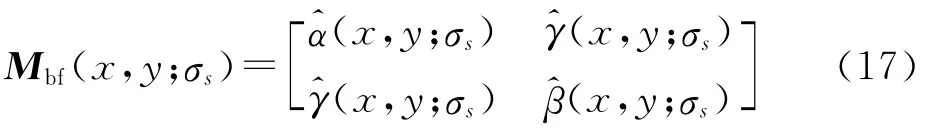
针对尺度不变性的问题，可采用文献［5］的方法将图像进行多尺度的分解，则由（17）式可以得到多尺度双边滤波自相关矩阵：

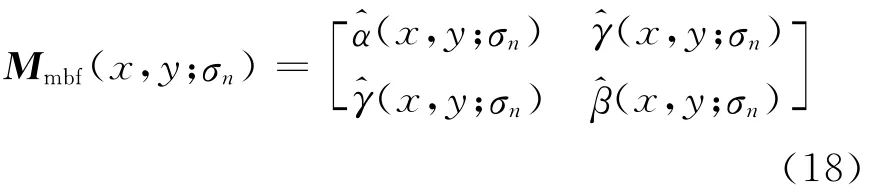
3 改进的特征点检测方法

3.1 基于局部结构的分组

同多尺度Harris算子没有重复剔除的机制一样，多尺度双边滤波有冗余特征点，借鉴文献［16］的方法采取分组的思想，将表示同一局部结构区域的特征点分在同一组。具体如下：

（1）在最大尺度的一层中，将检测到的每个特征点自成一组，并将各点加入该组。

（2）在次大尺度的一层中，对每个特征点分别寻找与已经分组的点最近点，若它们的距离不大于一个阀值，则添加到该最近点所在组中；否则开辟新的分组，将此点添加到新的分组中。

（3）重复步骤（2），直到遍历所有尺度图像的特征点，最终能得到若干分组。

3.2 最佳特征点的选取

在以上得到的各组结果中，选取一个最能代表该组局部结构的特征点。由文献［4］可知自相关矩阵的2个特征值有特殊的意义：其不仅表示该点处朝2个正交方向灰度有变化，还可以表示变化的剧烈程度。设λ1、λ2为自相关矩阵的2个特征值，记k＝λ1／λ2，此k值可以作为度量该点的信息。

在各分组中，计算出每组中各点在各自尺度下自相关矩阵的特征值以及相应k值，选取k值最大的点，记录该点的坐标和相应的尺度作为该区域结构的信息并作为最终的特征点。

4 实验结果与分析

为了测试提出算法的检测性能，在Windows XP操作系统下，采用Matlab编程软件，选用标准测试图像进行测试。

4.1 实验1：算法的准确度

特征点查全率、查准率可定义为：查全率R＝a／b；查准率P＝a／c；a为检测到的正确特征点数；b为图像实际的特征点数，c为检测到的特征点的数。

实验用Harris算法、Harris－Laplace算法和本文算法对256×256的灰度图像block进行检测，结果如图3所示。Harris方法中的滤波方差为1.5，k取0.06；本文和 Harris－Laplace算法均使用同样的尺度空间。空间方差为：

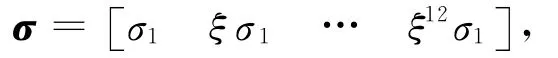
其中，σ1＝1.5；ξ＝1.2。实验各算法查全率、查准率见表1所列。

从实验数据分析可知，Harris算法和Harris－Laplace算法有相同的查全率，并且Harris查准率比Harris－Laplace高，说明Harris算法在一个适当的尺度下，能获得比Harris－Laplace更好的实验结果。

本文算法的查准率比 Harris－Laplace算法高，比Harris算法稍低，但查全率比Harris算法、Harris－Laplace算法都高。

图3 算法准确度测试

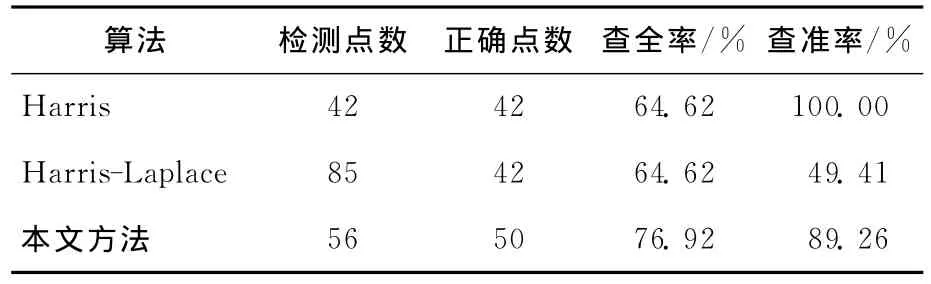
表1 3种方法检测特征点数准确度

4.2 实验2：去冗余点

实验用多尺度 Harris算法、Harris－Laplace算法和本文算法对256×256的灰度图像house进行检测，结果如图4所示。

图4 算法去冗余测试

多尺度Harris算法、Harris－Laplace算法和本文算法检测结果（本处去除了尺度信息的图像表示，均用中心点标记）见表2所列。

表2 3种算法去除冗余点数对比

由表2数据可知，本文算法可以有效地去除冗余特征点，并且从图4c、图4d中可得知本文算法得到的特征点准确度要高。

综上可得，本文算法能更准确地定位特征点的位置，而且能有效地去除冗余，得到的效果要比传统的Harris和Harris－Laplace算法更优。

5 结束语

本文通过研究 Harris、多尺度 Harris及Harris－Laplace特征点检测方法，发现其存在2个问题：① 弱特征点被忽略；② 多尺度Harris、Harris－Laplace方法存在较多冗余点。在Harris－Laplace方法的基础上提出一种改进的Harris特征点检测方法。实验结果表明，该方法与Harris、Harris－Laplace算法相比有更好的特征点定位功能，而且比Harris－Laplace有更强的去冗余能力。算法的不足之处是计算时间稍长。

［1］ 陈白帆，蔡自兴.基于尺度空间理论的Harris特征点检测［J］.中南大学学报：自然科学版，2005，36（5）：751－754.

［2］ 朱士杰，马 峻.一种改进的多尺度Harris角点检测算法［J］.电脑开发与应用，2010，23（6）：31－33.

［3］ 李红梅，黄梦涛，田爱玲，等.亚像素级标定角点提取新算法［J］.西安科技大学学报，2006，26（4）：536－540.

［4］ Harris C，Stephens M J.A combined corner and edge detector［C］／／Proc of the 4th Alvey Vision Conference，Manchester，UK，1988.doi：10.5244／C.2.23.

［5］ Mikolajczyk K，Schmid C.Scale ＆affine invariant interest point detectors［J］.International Journal of Computer Vision，2004，60（1）：63－86.

［6］ 朱丽娟.一种双边核函数的新Harris角点检测算法［J］.激光与红外，2013，43（5）：569－572.

［7］ Lindeberg T.Scale－space theory：a basic tool for analyzing structures at different scales［J］.Journal Applied Statistics，1994，21（2）：223－261.

［8］ Lindeberg T.Detecting salient blob－like image structures and their scale with a scale－space primal sketch：a method for focus－of－attention［J］.International Journal of Computer Vision，1993，11（3）：283－318.

［9］ 贺 强，晏 立.基于LOG和Canny算子的边缘检测算法［J］.计算机工程，2011，37（3）：210－212.

［10］ Tomasi C，Manduchi R.Bilateral filtering for gray and color images［C］／／Proc Int Conf Computer Vision，1998：839－846.

［11］ 余 博，郭 雷，钱晓亮，等.一种新的自适应双边滤波算法［J］.应用科学学报，2012，30（5）：517－523.

［12］ 胡 敏.连分式方法在数字图像处理中的若干应用研究［D］.合肥：合肥工业大学，2004.

［13］ 檀结庆，朱晓临，胡 敏，等.连分式理论及其应用［M］.北京：科学出版社，2007：105－115.

［14］ 胡 敏，檀结庆.基于Thiele型向量连分式插值的彩色图像放大方法［J］.合肥工业大学学报：自然科学版，2003，26（6）：1137－1140.

［15］ 杨兴明，陈海燕，王 刚.基于连分式的广义高斯分布的参数估计［J］.合肥工业大学学报：自然科学版，2012，35（7）：991－996.

［16］ 徐贤锋，檀结庆.一种改进的多尺度Harris特征点检测方

法［J］.计算机工程，2012，38（17）：174－177.