一类变换半群的秩

唐先聪

(淮阴工学院 数理学院，江苏 淮安 223003)

一类变换半群的秩

唐先聪

(淮阴工学院 数理学院，江苏 淮安 223003)

半群的秩定义为该半群最小生成集的基数；由于半群的秩类似于线性空间的维数，是反映半群生成问题的最重要的数字特征，因此研究半群的秩具有重要的理论意义，对半群秩的研究也是半群理论研究的重点问题之一。应用轨道理论，证明了变换半群 是非幂等元生成的，并证明了其元素可由幂等元生成的充要条件，以及非幂等元生成元素Sn(A,≤n)的生成方式，从而证明了得到了该半群的秩的计算公式 。

变换半群；轨道；秩

0 引 言

设S是半群，若存在S的非空子集T，使得S中的任一元素都可表示成T中元素的乘积，则称半群S可由T生成，称T为S的一个生成集，并记为S=〈T〉。半群S的秩rank(S)定义为S的最小生成集的基数，即rank(S)=min{|T|,〈T〉=S,T⊆S}。

设Xn={1,2,…,n}，Tn是Xn上的全变换半群记，Singn={α∈Tn:|imα|≤n-1}是Xn上的奇异变换半群。设α∈Jr={α∈Singn:|α|=r}(r=1,2,…,n-1)，称Z(α)=XnImα为变换α的亏集；当|Z(α)|=1时，记α唯一非独点型核类为αα-1，即αα-1={x,y:xα=yα}；

设α∈Singn，称以Xn={1,2,…,n}为顶点集，以E={(x,xα),x∈Xn}为边集的有向图∏α(Xn)=(Xn,E)为由Xn生成的α-子图；称∏α(Xn)的一个连通分支为α的一个轨道。设V是Xn的非空子集，α∈Tn，由于V⊆Xn是有限集，则存在正整数m，使对任意的l∈N都有Vαm=Vαm+l，则称Vαm为V的一个核心，记为Kα(V)。

设Ω是α∈Tn的一个轨道，则可依Kα(Ω)将轨道分类为：

圈型：Kα(Ω)=Ω，|Ω|≥2；

独点型：|Ω|=1；

柄圈型：Ω={x,xα，…，xαl+r=xαt}，(t,r>0)，|Ω|=t+r；

一般型：除前述三种以外的轨道。

引理1：设α∈Jn-1，则α没有一般型轨道。

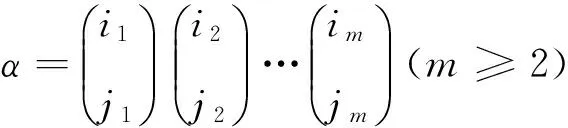
则 ⑴αα-1=[i1,j1]，Z(α)={im}；⑵ir-1=jr，jr-1≠ir(r=2,3,…,m)。

引理3: 设Sn是Xn上的对称群，则⑴rank(Sn)=2，(n=1,2)；⑵rank(Sn)=2，(n≥3)。

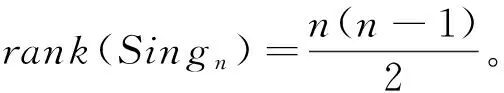
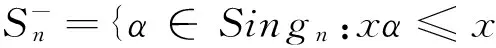
设A是Xn(n≥2)的非空集子集，Sn(A,≤)={α∈Singn:xα∈A且xα≤x(∀x∈A)}，不难验证Sn(A,≤)是Singn的子半群。

本文中，记|A|=k≥1，|XnA|=n-k≥1；SXnA定义为XnA的变换半群，SingXnA定义为XnA上的奇异变换半群(同理定义SingA)，SA-={α∈Singn:xα≤x}，其它未说明符号的含义参见文献[1]。

1 几个引理

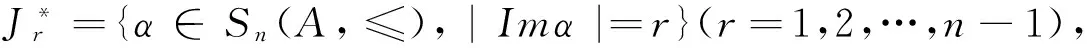
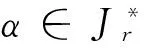
⑴若Z(α)∩A=φ，则取a、b∈Z(α)(a≠b)，构造变换：

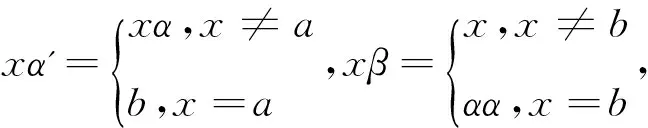
⑵若Z(α)∩A≠φ，则取b=min{Z(α)∩A}，a∈Z(α)(a≠b)，构造变换：

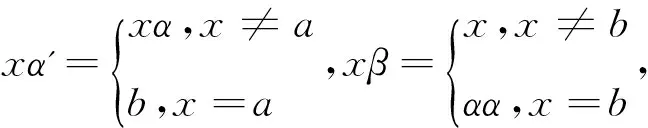
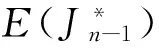
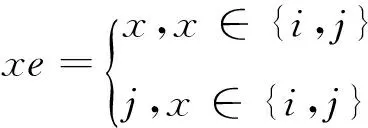
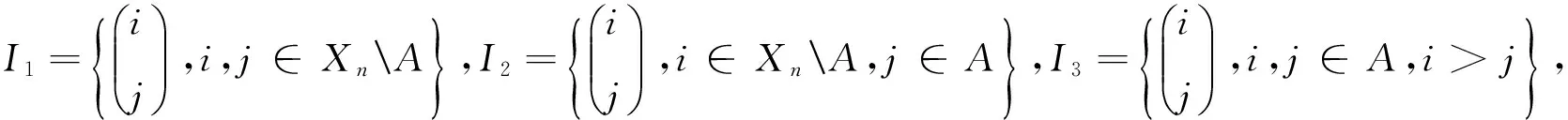
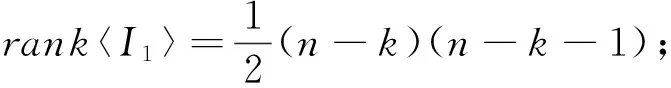
⑵〈I2〉是Sn(A,≤)的子半群，且rank〈I2〉=k(n-k)；

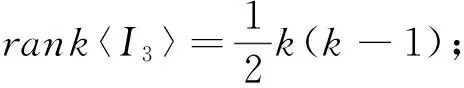
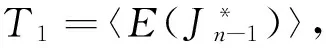
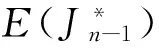
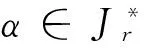
证：由引理6可知，只需证明上述引理在r=n-1时成立即可。

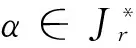
⑴设Ω={x,xα,…,xαk-1,xαk=x}为α的圈型轨道，则xαi∈XnA(i=0,1,…,k)，

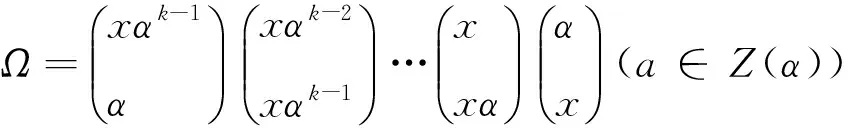
⑵设Ω={x,xα,…,xαt+r=xαt}为圈柄型轨道，则xαi∈XnA(i=0,1,…,t+r-1)，

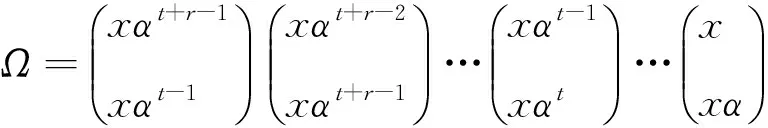
⑶设Ω={x,xα,…,xαk}为圈柄型轨道，且xαi∈XnA(i=0,1,…,k-1) ，但xαk∈A，

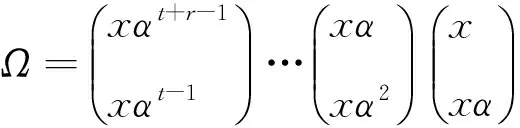
引理10：设T2={α∈Sn(A,≤):Z(α)∩(XnA)≠φ}，则

⑴设α∈T2，则α或不可由Sn(A,≤)中幂等元生成，或α∈〈I3〉；

⑵T2是Sn(A,≤)的子半群，且

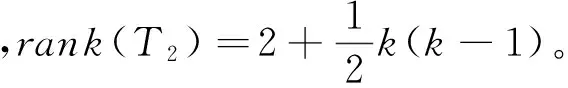
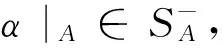
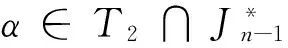
(2)不难验证T2-{α∈Sn(A,≤):Z(α)∩(XnA)=φ}是Sn(A,≤)的子半群。

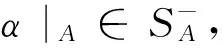
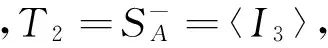
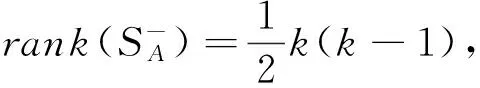
2 结论

定理：设Sn(A,≤)={α∈Singn:xα∈A且xα≤x(∀x∈A)}，则

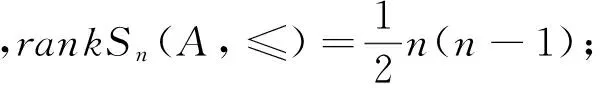
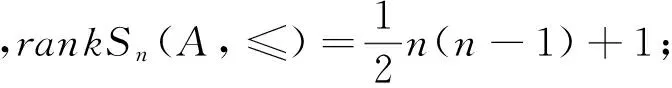
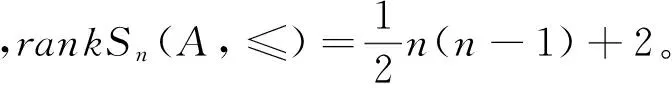
证明：由引理9、10可知：Sn(A,≤)=T1∪T2，又T1∪T2=〈I3〉，故

rankSn(A,≤)=rankT1+rankT2-rank〈I3〉

又由引理8、引理10可证得定理成立。

附：当n=2，3时的情形如下：

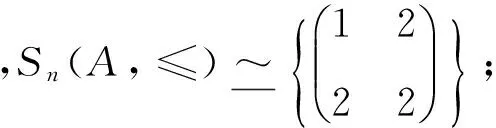
[1]J.M.Howie.FundamentalsofSemigrouptheory[M].Oxford:ClarendonPress,1995.

[2]J.M.Howie.Idempotentgeneratorsinfinitefulltransformationsemigroup[J].Proc.Roy.Soc.Edinburgh,1978,81:317-323.

[3]J.M.Howie.Idempotentrankinfinitefulltransformationsemigroups[J].Proc.Roy.Soc.EdinburghSect,1990,144:161-167.

[4]A.Umar.Onthesemigroupsoforder-decreasingfinitefulltransformations[J].Proc.Roy.Soc.Edinburgh，1992，120:129-142.

[5]J.M.Howie.Thesubsemigroupgeneratedbytheidempotentsofafulltransformationsemigroup[J].LodonMathSoc., 1966,41:707-716.

[6] 亨格福德.代数学[M].冯克勤,译.长沙：湖南教育出版社，1985.

(责任编辑：尹晓琦)

On the Rank of Certain Transformation Semigroups

TANG Xian-cong

(Faculty of Mathematics and Physics, Huaiyin Institute of Technology, Huai'an Jiangsu 223003, China)

The rank of a semigroup is the card of the minimum generating-set of the semigruop and is the most important number character of a semigroup. So it has important theory significance to study the rank of a semigroup, and it is one of the main problems on a semigroup. In this paper, a theorem the about the rank of Sn(A,≤n) was proved.

transformation semigroup; orbit; rank

2015-03-25

唐先聪(1970-)，男，湖南慈利人，助教，硕士，主要从事半群理论研究。

O152.7

A

1009-7961(2015)03-0017-05