单一供水模式下城市供水风险评价

盛 祥，王 恩

(1.苏州市环境监测中心，江苏 苏州 215002；2.环境保护部 南京环境科学研究所，南京 210042)

单一供水模式下城市供水风险评价

盛 祥1，王 恩2*

(1.苏州市环境监测中心，江苏 苏州 215002；2.环境保护部 南京环境科学研究所，南京 210042)

北方单一供水模式增加了城市供水风险，耦合模拟退火粒子群优化和模糊层次分析对供水指标体系进行优选，应用基于可变模糊集思想的多元联系数进行风险计算，构建了单一供水模式下城市供水风险评价模型。以济宁市六个行政区为例，分别进行风险计算，并应用模糊聚类分析法对模型计算结果进行合理性验证，为北方以地下水作为唯一供水水源城市寻求多元化供水模式提供理论依据。

供水模式；供水风险；评价模型；地下水

0 引言

我国北方由于缺乏充足的地表水资源，地下水长期处于严重超采状态，随着城市人口及经济的增长，加剧了与供水资源的矛盾[1-2]。地下水的过度开采，引发了较为严重的水文地质灾害。此外，由于地表水与地下水之间密切的水力联系导致的地下水污染也日趋严重[3]，在一定程度上更加剧了城市的供水风险[4-5]。

城市供水是城市的生命线工程之一，也是保障城市正常运转的重要基础设施。城市供水风险研究的目的是指导和建设适合城市可持续发展的城市供水系统，而该系统是一个极为复杂的动态系统，面临着许多不确定因素的影响。总结已有研究成果发现，传统城市供水相关研究主要考虑建立城市应急供水水源地保障供水水源的可持续性。为此，国内已有部分城市陆续开展“水源地突发性污染应急机制”研究与应对措施构建工作，与突发性供水水源污染事件相关的水源地污染风险评价研究也日益增多[6-8]。然而，城市供水是一个复杂系统，涉及到自然因素和人为因素，缺乏可操作的定量方法。目前，城市供水风险评价缺少研究，一方面由于不同城市的水资源开发利用模式不同、城市经济差异以及水资源时空分布规律的不同，导致很难构建统一的城市供水风险评价指标体系；另一方面，指标体系中一些指标怎样合理量化更需要进一步研究。如何合理确定城市供水风险评价指标体系及其评价等级标准以及如何处理模糊、随机等不确定性条件下各指标评价结果的不相容性，建立合适且易量化的供水风险评价指标体系已经成为城市供水风险研究的关键。

本文结合北方超采城市供水结构现状，从供水水源角度出发，建立以地下水为唯一供水水源的单一供水模式下的城市供水风险评价模型，为城市供水风险理论研究提供一定理论依据[9]。风险评价结果可以为城市决策者依据风险的大小，对城市供水模式可持续性进行选择与优化，对城市供水风险相对较大的区域进行优先管理[10]，优化现有城市供水系统，确保城市供水的可持续发展。

1 评价模型

城市供水风险是指城市供水水量和水质及其时空分布与水资源合理需求量之间的矛盾超过相应的阈值时所产生的矛盾。城市供水风险评价就是在综合考虑影响供水的自然因素和人为因素的基础上，建立相应的供水风险评价指标体系及其评价等级标准，根据不同的供水风险评价指标样本值，通过综合评价模型计算风险发生的可能性大小，来评价城市各子区域供水风险级别，为城市可持续供水提供理论依据。

利用基于模拟退火粒子群优化算法的模糊层次分析法，对评价指标权重进行计算并根据结果进行优选，用基于可变模糊集思想的多元联系数构建样本与评价等级之间的关系，定量地计算供水风险的大小，供水风险评价模型步骤分为六步。

1.1 考虑研究城市供水特点

本文仅考虑供水水源，通过专家咨询构建以地下水为水源的单一供水模式下的城市供水风险评价指标体系[11-14]{zj|j=1,2,…,m}，其中：m为评价指标个数。

1.2 利用基于模拟退火粒子群优化算法计算评价指标权重

考虑到评价指标之间存在一定的相关关系，因此，根据计算结果对评价指标进行优选，确定最终的评价指标体系zj。

1.2.1 模糊互补判断矩阵构造

通过咨询专家，采用九标度法对两两指标之间重要性进行比较，建立模糊互补判断矩阵：

P=(Pij)

(1)

式中：0≤Pij≤1，Pij+Pji=1(i，j=1,2,…,m)，Pij表示评价指标i与指标j的相对重要程度。

1.2.2 模糊互补矩阵一致性检验

若存在m阶非负归一化的向量w=(w1，w2，…，wm)T及正数a，满足：Pij=a(wi-wj)+0.5，称模糊互补矩阵具有满意的一致性。此时，权重向量确定方式如下：

(2)

如果模糊互补矩阵P非负归一化权重满足式(2)，则正参数a必定满足下式：

A≥0.5(m-1)

(3)

式中：a越大，权重差值越小，表明非常重视元素间重要程度差异；反之，表明不是很重视元素间重要程度差异。本文考虑到应该重视元素间重要程度的差异，选取a=0.5(m-1)。如果P不具有满意的一致性检验结果，则需要对模糊互补判断矩阵进行修正。设P的修正模糊互补判断矩阵为R=(rij)，R的各指标权重向量仍表示为w=(w1，w2，…，wm)T，采用常用的修正模糊互补判断矩阵一致性的优化模型：

(4)

rij+rji=1

(5)

(6)

式中：rij∈[Pij-d,Pij+d]∩[0,1]，i=1,2,…,m-1,j=i+1,…,m,rii=0.5,wj>0，称目标函数(CIC)为一致性指标系数，d为非负参数，其取值范围一般在[0,0.5]内选取。本文通过试算选取d值为0.3。

1.2.3 分析目标函数CIC

当CIC越小时，表示模糊互补判断矩阵P的一致性程度越高。其中：式(4)中的优化变量个数有m(m+1)/2个，包括了权重向量wj(j=1,2,…,m)和修正后的互补判断矩阵R=(rij)的上三角矩阵元素。

1.2.4 指标权重计算与筛选

利用给定CIC临界判断值，当CIC小于它时，可认为P具有满意的一致性，据此计算所得的权值向量就认为是可以接受的，本文选取的CIC的临界值为0.18。

邀请n位专家建立n个模糊互补判断矩阵P，利用模拟退火粒子群优化算法求解优化模型得到n组权重{wdi|d=1,2,…,n;i=1,2,…,m}[15，16]，选取评价指标体系中权重均值最大的前个评价指标，构成最终的北方地下水超采城市在单一供水模式下的城市供水风险评价指标体系{zi|i=1,2,…,l}。权重均值计算如下式：

(7)

1.3 构建城市供水风险评价等级标准

风险评价等级表示为：{xki|k=1,2,…,u;i=1,2,…,l}，其中：u表示评价等级分类数，1表示通过权重均值的计算筛选出的最终指标个数。而相应的风险评价样本集合为：{zsi|s=1,2,…,n;i=1,2,…,l}，其中：n表示评价样本数目。

1.4 选定评价等级标准数

选定评价等级标准数为5，即k=5。为了直观表述风险评价结果相对大小，将评价等级分为1到5，分别标记为“高风险”、“较高风险”、“一般风险”、 “较低风险”及“低风险”。若样本s评价指标i的特征值zsi随着评价等级的增大而增大。若样本s评价指标i的特征值zsi随着评价等级的增大而减小，则指标联系数分量usjk的隶属度函数根据实际物理意义进行选取。

指标联系数分量usjk∈[-1,1]。根据可变模糊集理论，usjk是评价等级k的一种相对差异度，为避免构造相对隶属度函数时需要考虑城市实际情况，本文采用公式(8)计算指标联系数分量的相对隶属度。

Isik=0.5+0.5usik,s=1,2,3,…n;

k=1,2,3,…,u

(8)

(9)

1.5 计算样本s与供水风险评价等级之间的多元联系数μs

利用相对隶属度归一化后的指标多元联系数分量，根据公式(10)计算指标多元联系数，利用公式(11)计算样本s与供水风险评价等级间的多元联系数μs。

μs=I'si1+I'si2i1+I'si2i2+I'si2i3+I'si5j

(10)

(11)

1.6 计算样本s的供水风险等级Ls

为了提高供水风险评价结果的可靠度，减少传统采用最大隶属度评判原则确定的样本最终评价等级的误差，通过计算特征值Ls作为评判样本s的风险评价等级值，并根据公式(12)的置信度准则判断供水风险评价等级。

(12)

(13)

式中：μsk为样本S与评价等级标准之间多元联系数分量。本文采取较为保守的策略选取λ值为0.7。

2 实例应用

本文以山东省济宁市为例，在分析供水水源影响因素的基础上，考虑了选择指标的可比性、合理性及资料收集的可操作性，咨询专家并借鉴国内外城市供水风险评价指标，确定了济宁市供水风险评价指标体系。其中：z1为生态环境用水率，z2为农业灌溉面积率，z3为单位面积农肥施用量，z4为万元农业产值用水量，z5为干旱指数，z6为万元工业产值用水量，z7为地下水资源供水模式率，z8为单位面积水资源量，z9为人均日生活用水量，z10为工业废水排放密度，z11为万元产值污水排放量，z12为人口密度，z13为人均生活污水排放量。

本文邀请8位专家对评价指标体系中两两指标间的重要性进行比较，建立模糊互补判断矩阵，用基于模拟退火粒子群优化算法分别计算上述矩阵，得到的指标权重计算，结果见表1。

表1 指标权重计算结果

注：表中σ为标准差，μ为均值。

由表1知，模型优化后得到的一致性指标系数值均小于0.18，小于临界值。通过计算指标权重的标准差与均值发现，变差系数CV的值均在0.3左右，相对来说较小，说明模糊互补判断矩阵比较均一。

选取评价指标体系中权重均值较大的9个评价指标，构成济宁市城市供水风险评价指标体系，根据指标的物理意义及其对城市供水的影响，构建济宁市单一供水模式下的城市供水风险评价等级标准，见表2。

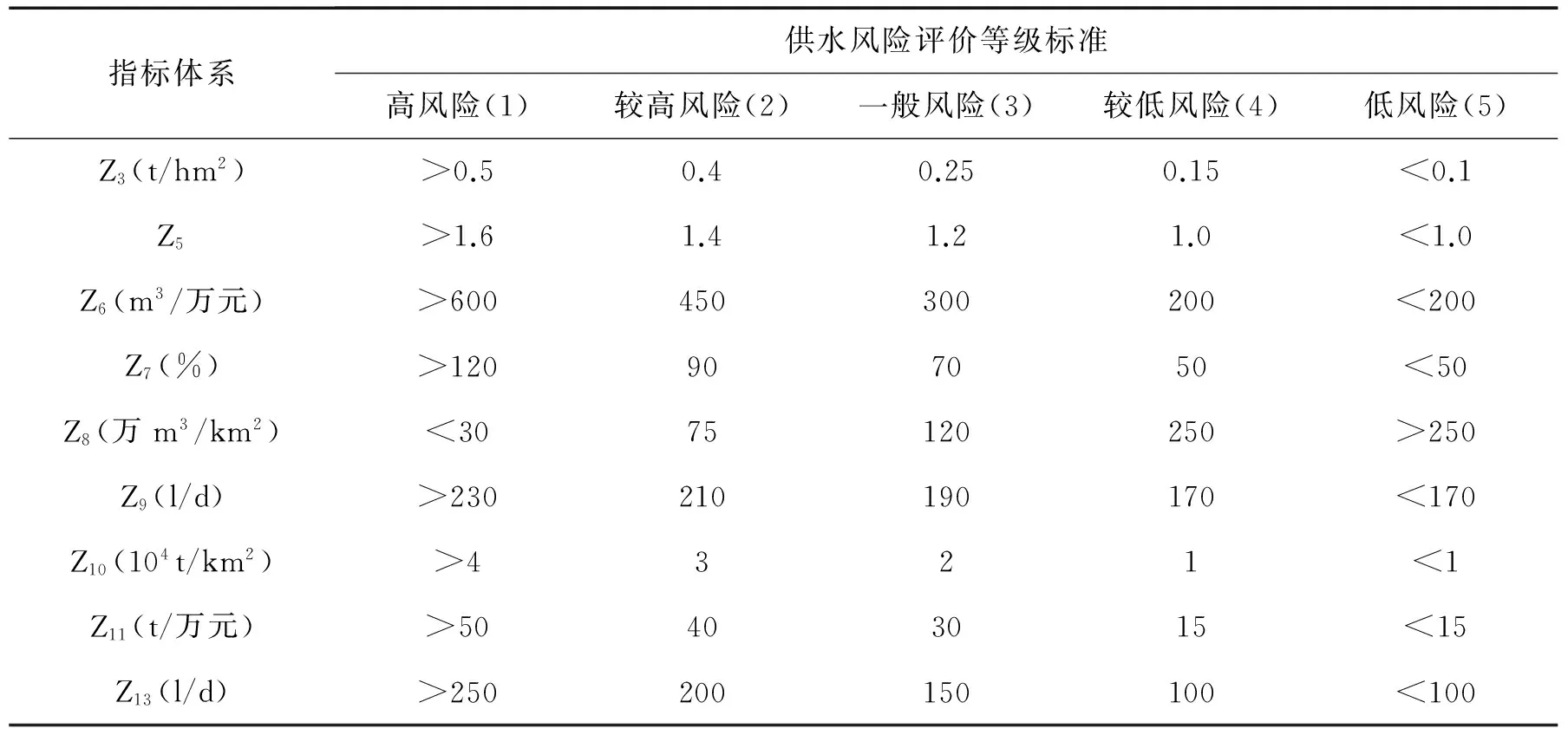
表2 济宁市供水风险评价指标等级

选取济宁市任城区、兖州市、鱼台县、嘉祥县、曲阜市和微山县六个行政区域(分别用A、B、C、D、E、F表示)作为评价对象，计算出六个区域的风险评价等级结果，详见表3～表5。

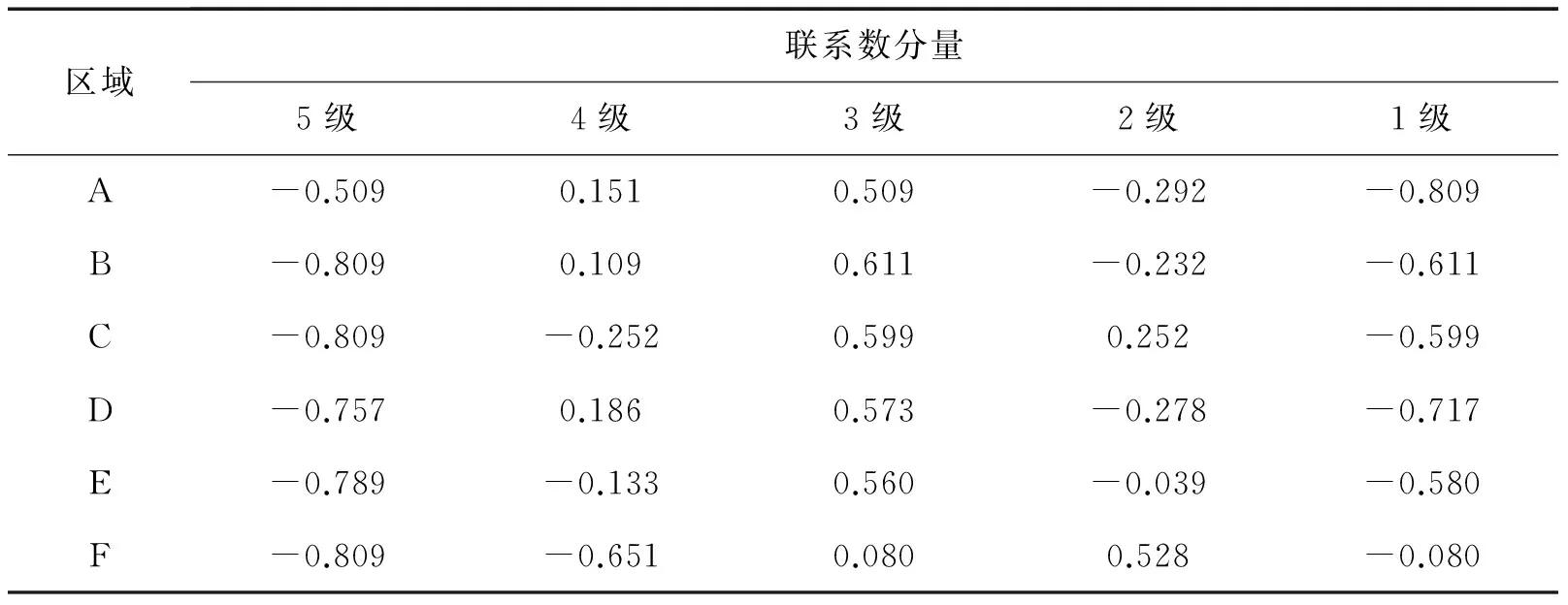
表3 多元联系数计算结果

表4 归一化相对隶属度计算结果

表5 六行政区供水风险评价等级

3 模型合理性分析

为分析本文提出的模型合理性，利用模糊聚类分析(FCM)[17]对原始样本进行聚类分析，各行政区域样本的模糊聚类等价关系矩阵见表6，给定置信水平λ=0.7条件下，原始样本可以分为A、B、D和C、E、F两大类，分类结果与供水风险评价结果一致，从而说明供水风险评价结果在给定置信水平λ=0.7条件下是合理的，结果见表6。

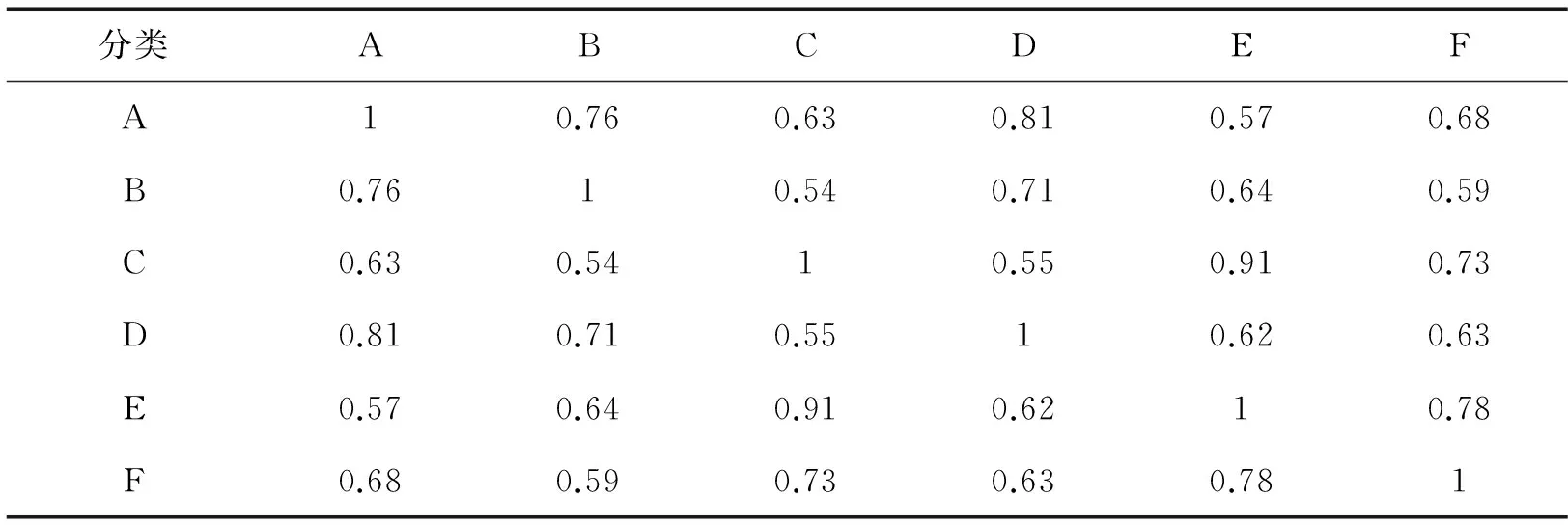
表6 模糊等价关系矩阵

4 结论

(1)城市供水风险受诸多非线性指标影响，本文耦合模拟退火粒子群优化和模糊层次分析对指标体系进行优选，减少了指标体系之间相关性影响，提高了模型精度。

(2)由风险评价模型结果可知，济宁市任城区、兖州市、嘉祥县城市供水风险等级处于3级的一般风险状态，而鱼台县、曲阜市和微山县供水风险等级处于4级的较低城市供水风险状态。总体来看，济宁市研究区供水风险相对最大，而微山县供水风险相对最小。因此，应优先考虑完善济宁市研究区供水模式，加强供水风险管理，探索多元化供水模式，从而提高城市供水可靠度。

(3)利用模糊聚类分析法对研究样本进行分类，验证了风险评价模型的合理性。

[1] 朱婷,李树平,刘隧庆.可持续城市水系统风险分析的应用及进展[J].中国给水排水,2007,23(16):18-21.

[2]HustonPT,KendallDR,FischerBW,etal.Applyingsecurityandvulnerabilityassessmentstolargewaterwholesalingagencies[C].USA:AmericanSocietyofCivilEngineers, 2003.

[3]FosterJA,McDonaldAT.Assessingpollutionriskstowatersupplyintakesusinggeographicalinformationsystems(GIS)[J].EnvironModellingSoftwater, 2000, 15(3):225-234.

[4] 吴小刚,张土乔.城市给水网系统的故障风险评价决策技术[J].自然灾害学报,2006,15(2):73-78.

[5] 王郑,王祝来,张勇,等.城市供水安全应急保障体系研究[J].灾害学,2006,21(2):106-109.

[6] 张羽,张勇,杨凯.基于时间特征指数的水源地突发性污染事件应急评估方法研究[J].安全与环境学报,2005,5(5):82-85.

[7] 陈燕海,张晓芬.城市供水水源应急预案探讨[J].水利发展研究,2003(6):31-33.

[8] 阎官法,贾涛.郑州市城市应急供水与应急生活供水定额研究[J].河南工业大学学报:社会科学版,2005,1(3):21-23.

[9]GriggNS.Waterwastewaterstormwaterinfrastructuremanagement[M].London:Lewispublishers, 2002.

[10]LiZehong,TangShangying,XuZhigu.Connotationandevaluationofwaterresourcesecurity-takingHubeiProvinceforexample[J].SafetyandEnvironmentalEngineering,2005,12(4): 38-41.

[11]JinJuliang,ChengJilin,WeiYiming.Informationentropybasedfuzzypatternrecognitionmodelforbasineco-environmentalqualityevaluation[J].JournalofSichuanUniversity:EngineeringScienceEdition, 2006, 38(1): 5-9.

[12]MenBaohui.WangZhiliang,LiangChuan,etal.Applicationofmatterelementmodeltoevaluatingonofresourcescarryingcapacityofregionalgroundwater[J].JournalofSichuanUniversity:EngineeringScienceEdition, 2003, 35(1): 34-37.

[13] 陈思,高军省.基于多元联系数的灌溉水质综合评价[J].水资源与水工程学报,2011,22(5):103-106.

[14] 张清河.多元联系数在地基处理方案模糊优选中的应用[J].水文地质工程地质,2005,32(6):112-115.

[15] 李媛媛,曲雯毓,栗志扬,等.一种快速收敛粒子群优化算法在云计算中应用[J].华中科技大学学报：自然科学版,2012,40(Z1):34-37.

[16] 张国华,张展羽,邵光成,等.基于粒子群优化算法的灌溉渠道配水优化模型研究[J].水利学报,2006,37(8):1004-1008.

[17] 陈守煜,李庆国.一种新的模糊聚类神经网络及其在水资源评价中的应用[J].水利学报,2005,36(6):662-666.

(责任编辑：侍建旻)

Urban Water Supply Risk Assessment under Single Supply Mode

SHENG Xiang1，WANG En2*

(1.Suzhou Environmental Monitoring Center, Suzhou Jiangsu 215002, China;2. Nanjing Institute of Environmental Sciences, Ministry of Environmental Protection, Nanjing 210042, China)

The use of single water supply mode in North China enhances urban water supply risks. In this study, the simulated annealing particle swarm optimization and fuzzy analytic hierarchy process were coupled and used to select the optimal water supply index system. The water supply risks were computed via the multi-element connection number based on the idea of variable fuzzy set. Then an urban water supply risk assessment model under the single water supply mode was constructed. With the six districts in Jining city as examples, their water supply risks were computed separately. Then the reasonableness of the model-based computations was validated using the fuzzy clustering analysis. This study provided a theoretical basis for exploration of multiple water supply modes in many cities in North China, where groundwater is the only source of water supply.

water supply mode; water supply risk; assessment model; ground water

2015-04-27

国家重点基础研究发展计划(973计划)(2006CB403204)

盛祥(1981-)，男，江苏宿迁人，工程师，硕士，主要从事环境管理及承载力研究；*为通讯作者。

F

A

1009-7961(2015)03-0083-06