SSSC的选址及网损优化研究
2015-03-06庄海军任晓菲
庄海军,任晓菲
(1.东北电力大学 电气工程学院,吉林 吉林 132012;2.河南省郑州市供电公司计量部,郑州 450000)
电力系统网络损耗与功率在网络中的分布有关,所以控制潮流的合理分布能够减少网络损耗[1-2]。静止同步串联补偿器(SSSC)作为新型的柔性交流输电系统(FACTS)装置,可以等效成一个串联的同步电压源,通过改变电压或相位来改变输电线路的等效阻抗,能够快速调节系统潮流与系统电压,并可抑制次同步谐振与阻尼功率振荡[3-5]。而且SSSC安装在网络的不同位置,可使潮流分布情况不同。因此确定SSSC的合理安装位置,通过SSSC最优参数的选择,控制线路传输的功率对优化系统网损、提高系统运行的可靠性和经济性具有一定的现实意义。本文对SSSC的最佳安装位置和含SSSC的网损优化计算进行了研究。
1 SSSC等值模型的建立
SSSC的基本结构由耦合变压器、电压源型逆变器、直流环节组成,其中耦合变压器串联在输电线路中,直流环节一般为储能器、直流电源或电容器,如图1所示。
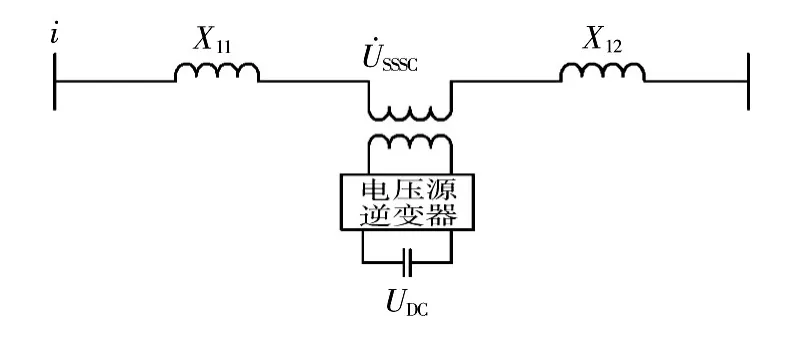
图1 SSSC基本结构Fig.1 SSSC basic structure
SSSC的数学模型是研究SSSC的基础,当只考虑静态模型时,SSSC可等效为一个幅值和相位均可控的且与电网同频率的交流电压源,如图2示。其中代表发送端的电压代表接收端的电压,代表SSSC输出的电压,r+jx为线路阻抗。这种SSSC模型具有理论清晰、结构简单的特点,同时对研究SSSC的功能及其对输电系统的潮流控制也具有绝对优势。

图2 SSSC等效模型Fig.2 SSSC equivalent model
SSSC加入到线路中改变了网络的结构,为了在潮流计算中可以最大限度地利用传统潮流计算中雅可比矩阵形成的公式和经验,将SSSC对系统的贡献转移到对应线路的两侧节点上,形成改进的等效注入功率模型[6],如图3所示,该模型可以在潮流计算中不必引入新的状态变量。

图3 等效注入功率模型Fig.3 Equivalent power injection model
等效注入功率与SSSC的控制参数之间的关系为

式中:δ为Usssc超前Ui的角度;g=r/(r2+x2);b=- x/(r2+x2);θij= θi- θj。
2 SSSC的选址
电力系统在正常或紧急事故情况下,为了综合反映系统的过负荷情况,可利用线路有功潮流性能指数来表征[7],其定义为

式中:Plm为支路m的有功潮流;为支路m的额定传输容量;n为指数系数;wm为支路m权系数,反映支路故障对系统的影响;αm为支路中并联线路数;NL为系统的总支路数。这样定义的PI参数可以概括地反映系统的安全性。
由于主要调节有功功率在网络中的分布,利用直流潮流计算求出节点注入有功对支路有功Plm的影响系数矩阵为θ=XP,根据其线性特性,有


则节点n注入的有功对支路有功(节点i流向节点j)影响的系数矩阵为

式中:xlm为支路m的电抗;xin、xjn为矩阵x中第i行第n列和第j行第n列的元素。
故当支路m为安装SSSC的线路时,该支路的有功潮流为

当支路m没有安装SSSC时,有功潮流为

由式(1)和式(6)可知,通过控制SSSC等效电压源的幅值与相角,可调节SSSC对Plm补偿方式与补偿大小。故本文提出用式(2)中PI对SSSC等效电压源的幅值与相角取偏导,即

根据PI的定义可知

设支路k为安装了SSSC的线路,而m≠k,则根据式(6)、式(7)可知

根据式(1)得到
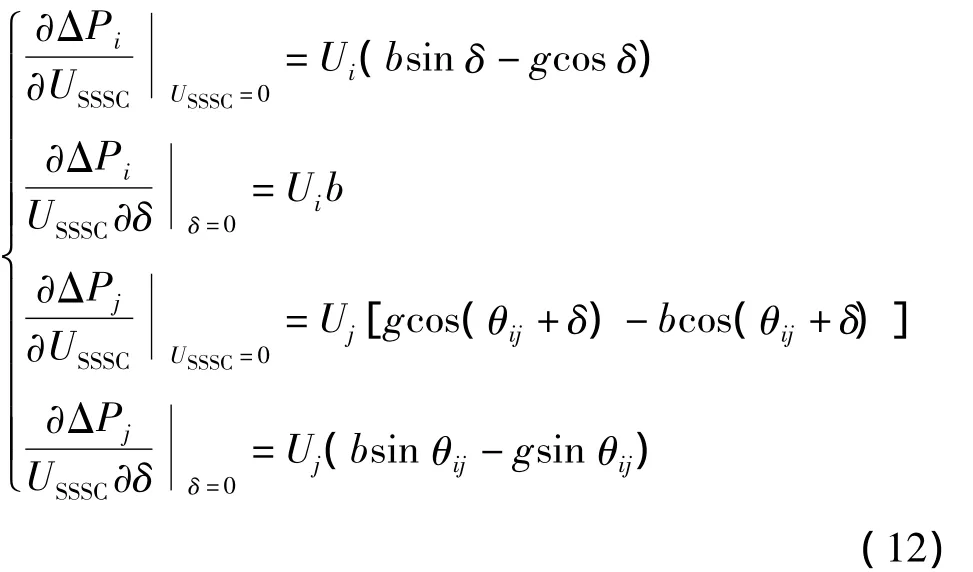
3 含SSSC系统的网损优化
得到SSSC最优安装位置后,可建立含SSSC系统的网损优化数学模型,并采用改进粒子群算法,在满足相应约束条件下,得到含SSSC控制参数的最优控制变量,并使潮流分布合理,达到优化网损的目的。
3.1 网损优化数学模型
3.1.1 目标函数
在潮流计算中,除平衡节点外,其他节点的有功功率都是给定的,所以全网有功功率损耗最小等同于平衡节点注入有功功率最小。若以第n个节点作为平衡节点,则目标函数可写为


3.1.2 约束条件
当系统未装设SSSC时,等式约束为普通的潮流方程,即

由于n为平衡节点,则Un、δn为已知Gnn为常数,目标函数可简化为
当系统装设SSSC后,含有SSSC线路的潮流方程发生变化,约束变为
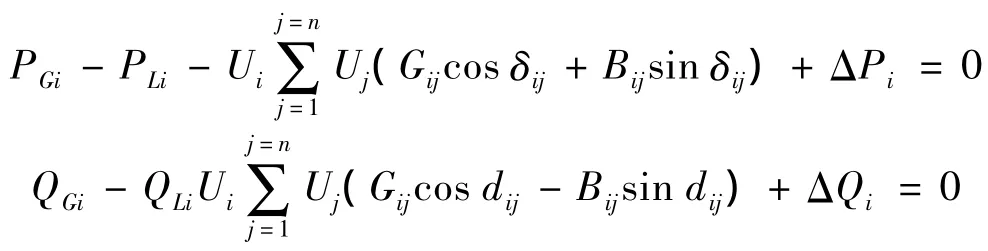
和原来潮流方程相比,式中ΔPi、ΔQi为SSSC对网络的影响,即式(1)表示附加注入功率。
考虑SSSC自身的运行约束为

以SSSC所在线路从节点i流向节点j的有功功率作为控制目标约束:
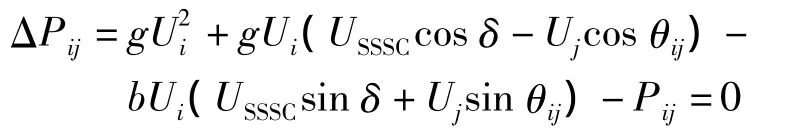
在不等式约束条件中,不仅包含传统计算节点电压幅值、变压器档位、电容、电抗器组数、发电机出力等运行参数约束,还包含SSSC电压源的幅值和相角约束,即
式中依次为:节点电压上下界约束;有载调压变压器分接头的档位约束;电容、电抗器组的无功容量约束;发动机有功功率容量上下界约束;发动机无功功率上下界约束;SSSC等效电压源幅值约束;SSSC等效电压源相角约束。
3.2 改进粒子群优化算法
粒子群优化算法(PSO)在编码过程中首先初始化一群随机控制变量粒子,然后粒子群追随当前最优粒子在解空间中通过迭代找到最优解。设d维搜索空间中的第i个粒子的位置和速度分别为Xi=(xi,1,xi,2…xi,d)、Vi=(vi,1,vi,2…vi,d),在每次迭代中,粒子通过追踪两个最优解更新自己:一个为本身最优解pbest;另一个为整个种群目前最优解gbest。在找到这两个最优解时,粒子根据以下公式更新自己的速度和位置:

式中:w为惯性权重;c1、c2为正的学习因子,r1、r2为0到1之间均匀分布的随机数。
同其它进化算法一样,PSO算法也容易陷入局部极值,导致算法早熟。因此,为克服PSO算法的局限性,本文提出一种基于杂交概念的改进粒子群算法来求解网损优化问题。根据遗传算法中杂交的原理和概率选取一定数量的粒子放进杂交池中,然后粒子随机两两杂交,产生同样数量的子代粒子,并取代父代粒子继续进行优化。这使得粒子可以有效避免陷入局部最优,增强了算法的全局搜索能力。
子代位置由父代位置进行算术交叉得到:

或

式中:p为0到1之间的随机数。
子代的速度由下式计算:

或

对于惯性权重w也进行了动态处理,惯性权重w控制着粒子的先前速度对当前速度的影响程度,改变其取值可以调整算法全局和局部搜索能力的平衡。本文中w为

式中:maxDT为最大迭代次数,t为目前迭代次数。
在网损优化模型中进化算法需要处理约束优化问题,约束条件的处理至关重要。而PSO算法是一种无约束的搜索技术,缺乏明确的约束条件处理机制。本文提出采用动态的准则对约束条件进行特殊处理。
约束条件的动态处理方法将最优潮流问题的目标函数和约束条件分开处理,目标函数用来评估解的有效性,约束条件仅用来判断解的可行性,动态地分配种群去优化不同优化难度的约束条件。
设一个子群对某约束条件的违背程度为Gi),由于不同约束条件的违背程度大小不同,为消除差异,可采用违背率。约束条件i的违背率为

根据每个约束条件的优化难度违背率为其分配子群规模,根据文献[8]的思想,为优化条件指定为其优化的子群:

根据式(17),采用轮盘赌策略,将有较多的子群优化较难的约束条件,而较容易的约束条件会有很少甚至没有子群对其进行优化。这样动态地处理约束条件,针对性更强、速度更快,算法适应性更高。同时,对各个待优化的变量进行了搜索区域的限制,设置了region数组,对粒子群优化结果进行位置限制,以免难以搜索最优值,减少迭代次数。
3.3 基于PSO的含SSSC系统的网损优化过程
选取式(13)表示的网损最小的目标函数作为算法的适应度函数,基于改进粒子群算法的网损优化计算的详细步骤如下:
1)设置系统参数,根据选址程序确定UPFC安装支路号,并指定region数组的上下界值。
2)在满足region条件下随机赋予种群中每个粒子即控制变量初始值和初始迭代步长,对于每个控制变量粒子,根据目标函数式(13)进行一次计算。
3)评价控制变量的适应值,将控制变量和目标初始值存储在各微粒的pbest中,将所有pbest中最优控制变量值和目标值存储于gbest中。
4)进入主循环,根据式(16)更新惯性因子w,迭代次数加一次。
5)根据式(15)进行杂交处理,计算控制变量粒子迭代速度 v,若 v≥Vmax,则 v=Vmax,若 v≤-Vmax,则v=-Vmax;根据式(14)计算控制变量粒子的位置,若控制变量粒子在任一维超出region所设搜索范围,则设置该控制变量粒子的位置为搜索空间的极限值。
6)应用牛拉法进行一次潮流计算和目标函数计算,再次评估每个控制变量粒子的目标函数值,并根据动态准则进行约束条件判断,选取可行粒子。
7)判断是否更新每个控制变量粒子的pbest和整个种群的最优控制变量粒子gbest,进行pbest与gbest粒子更新;判断是否满足算法的停止条件,满足则转向步骤8),否则转向步骤4)。
8)输出最优解,即最后一次迭代后的gbest,完成目标函数网损的计算。
4 算例分析
基于上述理论分析,以IEEE-14节点系统为例确定SSSC的最佳安装位置并进行网损优化计算。根据SSSC最佳安装位置的确定方法,将最有可能安装SSSC的支路灵敏度因子计算结果列在表1中。本算例中式(2)的n=2,wm=1.2。

表1 灵敏度计算值Tab.1 Sensitivity calculated value
在对SSSC进行选址的基础上,寻找最优控制变量实现网损优化,其中PSO的参数设置如下:wmax=1.0;wmin=0.5;粒子数目 n=40;学习因子c1=c2=2.05;最大迭代次数maxDT=1000。为了验证本文方法的性能,在同样的系统和相同的初始条件下,进行了优化前后的比较,计算结果如表2所示。

表2 网损优化结果Tab.2 Network loss calculated value
从表2中可以看到,当利用改进粒子群算法进行电力系统优化计算时,可在一定程度上降低网损并改善电压水平。当在系统中安装SSSC并利用灵敏度法进行SSSC选址时,将SSSC安装于功率分布较为不合理的线路上,利用PSO进行网损优化时,在改善电压水平和降低网损方面的作用得到进一步加强,并比安装在其他线路上时的效果更为明显。这说明了SSSC在调控潮流、降低网损上的作用,同时验证了选址方法的正确性和网损优化模型与优化算法的有效性。
5 结论
1)推导出了含SSSC线路的基于等效电压源模型的改进附加注入功率表达式。
2)利用一种基于直流潮流模型的灵敏度系数判别法确定了SSSC的最佳安装地点。
3)在未破坏网络节点导纳矩阵对称性前提下,将其分别引入到网损优化目标函数的等式约束条件和不等式约束条件中,建立了含有SSSC进行网损优化的数学模型。
4)将改进粒子群算法运用于含有SSSC的网络中进行网损优化模型的求解,通过算例分析验证了所建优化模型的正确性。
[1] 谢大为.柔性交流输电技术的发展及其应用[J].电力自动化设备,2007,27(2):16-19.XIE Dawei.Development and applications of flexible AC transmission systems[J].Electric Power Automation Equipment,2007,27(2):16-19.
[2] 李晋园,汤强,向晖,等.FACTS技术及其在电力系统中的应用[J].电工电气,2011,10(1):38-41.LI Jinyuan,TANG Qiang,XIANG Hui,et al.FACTS technology and its application in power system [J].Electrical Apparatus,2011,10(1):38-41.
[3] 刘隽,李兴源,姚大伟,等.静止同步串联补偿器与静止无功补偿器的相互作用分析与协调控制[J].电网技术,2008,32(1):20-25.LIU Jun,LI Xingyuan,YAO Dawei,et al.Analysis on interaction between static synchronous series compensator and static var compensator and their coordination control[J].Power System Technology,2008,32(1):20 -25.
[4] 郭成,李群湛.基于改进PSO算法的SSSC广域阻尼控制器设计[J].电工技术学报,2010,25(l):151-158.GUO Cheng,LI Qunzhan.SSSC wide- area damping controller design based on improved particle swarm optimization[J].Transactions of China Electrotechnical Society,2010,25(l):151-158.
[5] 周俊宇.静止同步串联补偿器在电力系统中的应用综述[J].电气应用,2006,25(4):51-54,118.ZHOU Junyu.Application of SSSC in power system[J].Electrotechnical Application,2006,25(4):51-54,118.
[6] 刘前进,孙元章,黎雄,等.基于功率注入法的UPFC潮流控制研究[J].清华大学学报:自然科学版,2001,41(3):55-58.LIU Qianjin,SUN Yuanzhang,LI Xiong,et al.Research on UPFC flow control based on power injection[J].Journal of Tsinghua University:Science and Technology,2001,41(3):55 -58.
[7] 孙福荣.使用灵敏度因子优化UPFC布点[J].继电器,2004,32(22):1-3.SUN Furong.Optimizing location of UPFC using sensitivity factors[J].Relay,2004,32(22):1 -3.
[8] 刘衍民,牛奔.新型粒子群算法理论与实践[M].北京:科技出版社,2013.LIU Yanmin,NIU Ben.Theory and practice of new particle swarm algorithm[M].Beijing:Science Press,2013.
