微电网分布式电源的分层控制策略研究

黎金英，艾 欣，邓玉辉

(华北电力大学 新能源电力系统国家重点实验室，北京 102206)

微电网是由分布式电源(Distributed Generation，DG)、储能装置、能量变换装置、负荷、保护装置等组成的小型电力系统。微电网的2种基本运行模式是:正常情况下，微电网和常规主电网并网运行，作为常规主电网的补充，称为并网运行模式;当检测到主电网发生故障(如负荷不平衡、单相对地短路、两相对地短路等)使得电能质量不能满足本地供电要求时，微电网将会迅速和常规主电网断开，独自对本地负荷进行不间断供电，具有不间断电源(Uninterrupted power supply，UPS)功能，称为孤岛运行模式［1］。不管是并网运行还是孤岛运行，都需要对各自子单元进行有效的质量控制，使其输出电压的频率和幅值在一定范围内，满足电能质量要求［2］。微电网中的分布式电源通过电力电子设备接入配电系统，其主要设备为逆变器，控制策略可分成 PQ控制、U/f控制和下垂控制(Droop控制)［3］。对于输出功率随机的电源，一般采用PQ控制，该控制方法可以实现最大能源利用效率;对于功率可以调节的电源，由于没有输出功率约束，因此可以实现U/f的控制，从而保证微电网频率和电压的稳定性。文献［4］介绍的微电网中分布式电源的控制主要包括主从控制(Master-slave control)、对等控制(Peer-to-peer control)和分层控制(Hierarchical control)3种类型，论述了分层控制是解决微电网中各元件协调控制的有效途径。文献［5］研究了微电网的2种综合控制策略:主从控制策略和对等控制策略。文献［6］提出了微电网分层控制的概念。文献［7］在研究交直流微电网的构成和各种运行模式的基础上，提出电压分层协调控制策略，实现微电网内的有功功率平衡，但是没有考虑到微电网电压和频率的稳定。文献［8］研究的微电网分层控制主要包括2层，其中:上层的微电网中心控制器(MGCC)根据分布式电源出力和微电网内的负荷需求变化，调节底层分布式电源控制器的稳态平衡点和负荷投切。文献［9］提出的嵌套分区算法对电力系统进行无功/电压分区，然后对相应区域中负荷节点电压对负荷增长水平灵敏度最大的节点进行无功补偿。根据不同的微电网分层控制，本文提出了一种适用于微电网分布式电源的分层控制策略—改进下垂控制法，通过Matlab/simulink进行仿真验证，结果表明了微电网中分布式电源分层控制策略的有效性。

1 微电网基本结构

微电网的模型结构如图1所示，主要包括交流母线、直流母线、DC/AC逆变器、AC/DC整流器、DC/DC直流变换器、负荷和分布式电源(如光伏、风力发电和储能等)。

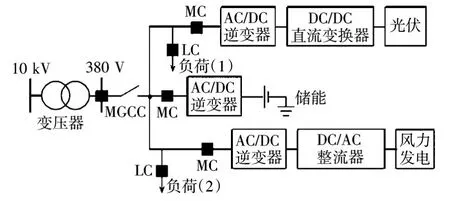
图1 微电网结构Fig.1 Microgrid structure

文献［10］提出微电网中心控制器(Microgrid central controller，MGCC)、负荷控制器(Load controller，LC)和微电源控制器(Microsource Controller，MC)间需建立可靠的通信连接。微电网中心控制器安装在中压-低压变电站，用来对微电网进行统一的控制，并负责微电网和主电网之间的通信和控制;负荷控制器和微电源控制器从属于微电网中心控制器，分别对负荷和微电源进行控制。

2 微电网分层控制策略

本文提出的微电网分布式电源的分层控制(Hierarchical control)主要包括2层，即初级控制(primary control)和二级控制(secondary control)，如图2所示。

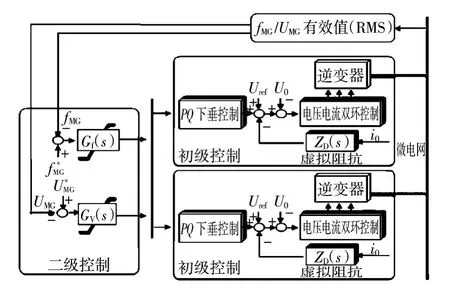
图2 微电网的分层控制结构Fig.2 Microgrid control hierarchical structure

在该控制策略中，每一层独立完成自己的控制任务，通过通信向下层传达命令，并且在向下层传达命令时不影响系统运行的稳定性。初级控制采用改进下垂控制的方法，主要通过操作层运行，直接运行控制，完成对分布式电源的控制。同时，通过对输出电压幅值和频率的控制完成对各逆变器电网接口输出的有功功率和无功功率分配，实现并联分布式电源的均衡和优化。二级控制通过初级控制信号重新控制逆变器的输出电压幅值和频率，使之重新达到平衡，实现系统运行的稳定性。

2.1 微电网的初级控制策略

微电网的初级控制(Primary control)如图3所示。

2.1.1 下垂控制原理

下垂控制法是分层控制中常用的一类控制算法，基础是分布式电源的间接功率控制法，如图4所示［11］。

根据图4可得流向公共连接点的功率表示为

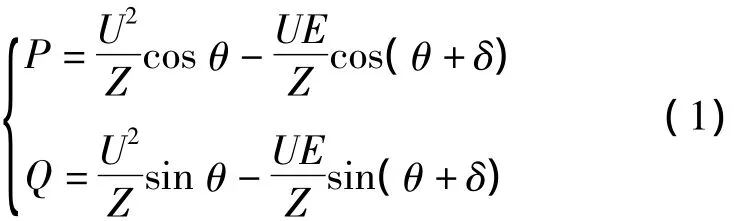
当Z∠θ=R+jX时，式(1)可写成

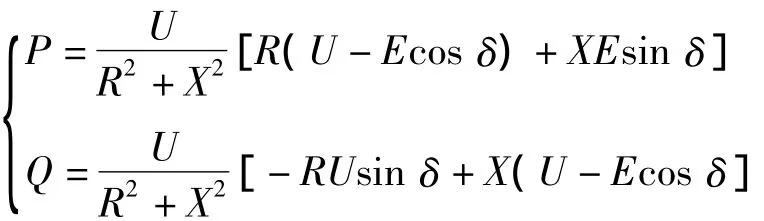
因此，有

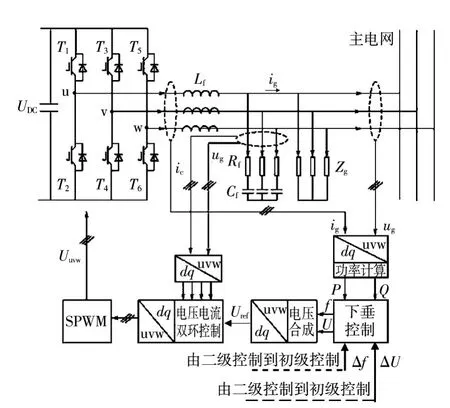
图3 初级控制系统图Fig.3 Primary control system

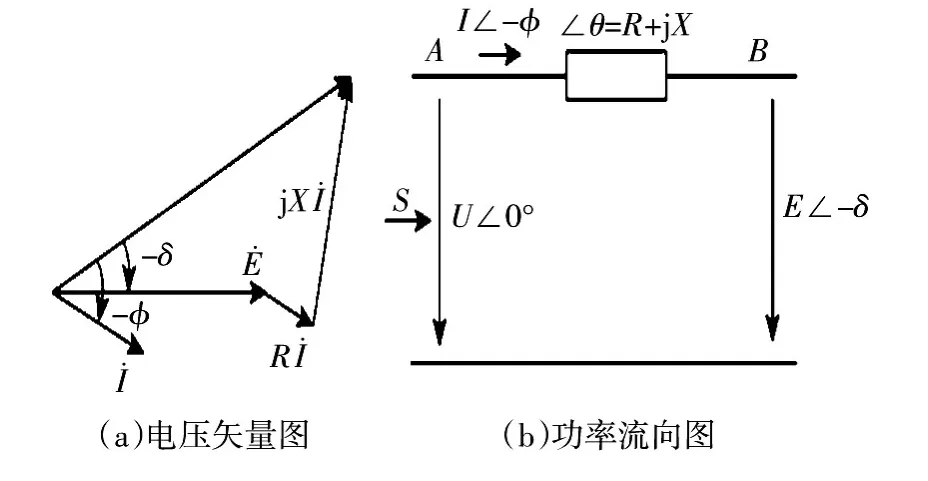
图4 分布式电源并网的等效线路Fig.4 Equivalent circuit of distributed generators grid-connected

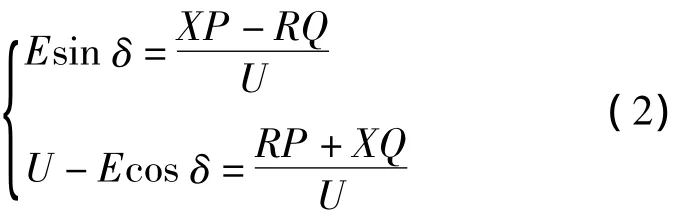
当分布式电源逆变器通过电感性线路连接到电网时，R≪X，电阻R可以忽略不计。若功率角δ很小，则 sin δ≈δ，cos δ≈1。式(2)可写成

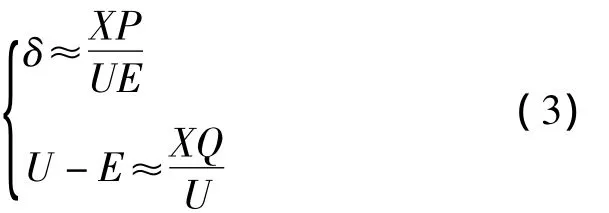
对于R≪X，功率角δ较小，且U-E差异较小。从式(3)可以看出，频率(或功率角δ)可通过调节有功功率P来控制，而逆变器的电压可通过调节无功功率Q来控制。对于分布式电源供电的负荷或微电网，不同的分布式电源处电压不可能有完全相同的频率和幅值，这是由它们之间频率和幅值微小差异造成的。相反，如果根据各功率变换器产生的有功功率和无功功率所形成的函数来控制它们的电压频率和幅值，整个系统将会找到一个平衡点，这可以保证控制器具有功率分配能力。因此通过调节分布式电源的有功功率和无功功率出力即可控制微电网的频率和幅值，这就衍生出了频率和电压的下垂控制方法，可以表示为

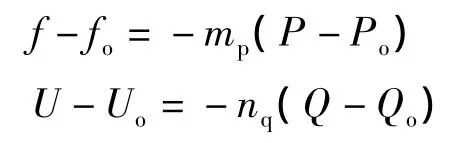
式中:fo为逆变器输出的额定频率;Uo为逆变器输出的额定电压;mp、nq分别为有功功率下垂系数和无功功率下垂系数;P为逆变器实际输出的有功功率;Q为逆变器实际输出的无功功率;Po、Qo分别为额定的有功功率和无功功率。

在低压微网中，线路阻抗比值较大，线路电阻R不能忽略，有功功率和无功功率存在较强耦合。传统下垂控制已经不能满足低压微电网控制的需求［12］。因此，本文提出一种改进型P-f和Q-U的功率耦合下垂控制策略。

2.1.2 改进下垂控制

在低压微网中，有功功率和无功功率对电压和频率的控制存在耦合关系。在一般情况下，X和R在优化调节电压和频率的下垂控制中都必须考虑。根据文献［13］可知，这里引入了一个正交线性族转变换矩阵T，将有功功率P和无功功率Q修正为P*和为 Q*，即

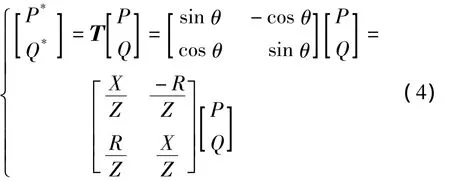
将式(4)代入式(2)，有

考虑到功率角 δ很小，sin δ≈δ，cos δ≈1，则式(5)可写成

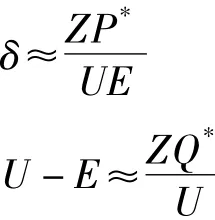
综上，假设 P*≈P，Q*≈Q，Q*≈ -Q，Q*≈P，令

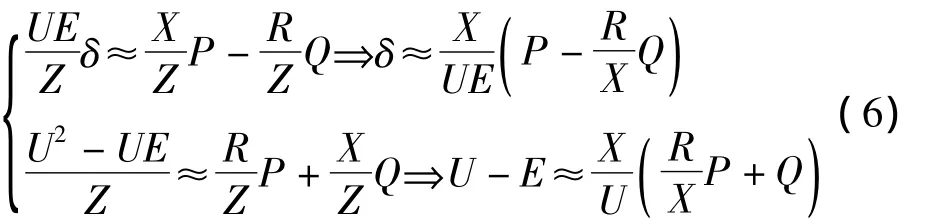
从式(6)可以看出，功率角δ和电压幅值需通过 P和Q的耦合调节来控制。根据上述原理可推出考虑阻感比的下垂控制通用表达式为

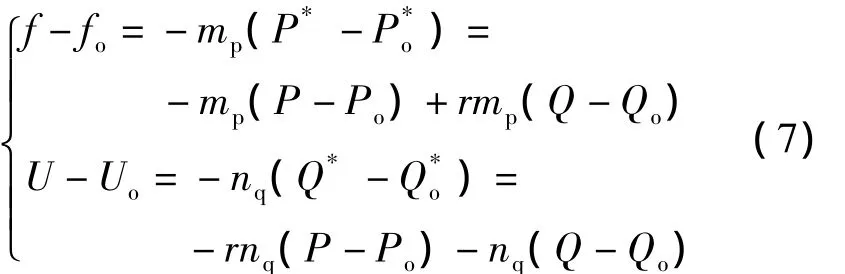
当r=0时，式(7)即为传统下垂控制。由式(7)可得如图5所示的有功功率和无功功率耦合的P-f和Q-U下垂控制框图。

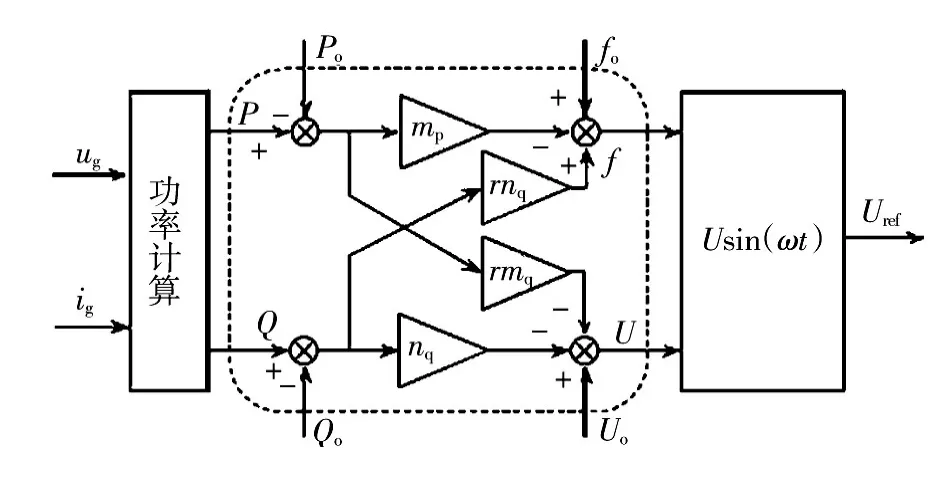
图5 P－f和Q－U下垂控制框图Fig.5 Block diagram of P－f and Q－U droop control

2.1.3 电压电流双环控制

在逆变器的控制系统设计中，一般采用双闭环比例积分(Proportional integral，PI)控制器，即采用电压外环和电流内环的控制方法。电压外环主要是维持中间交流侧uodq的稳定，一般采用PI控制器。电压控制的数学模型可以表示为［14］

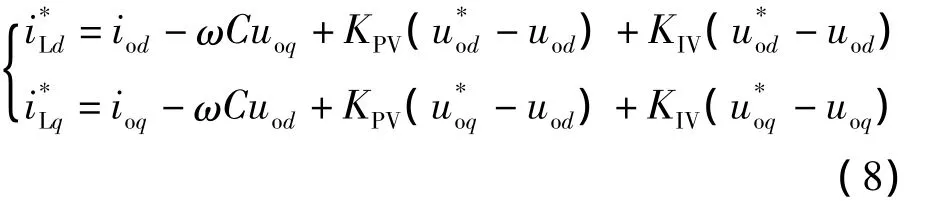
电流内环主要是按照电压外环输出的电流指令进行电流控制，一般采用PI控制器，电流控制的数学模型可以表示为［15］

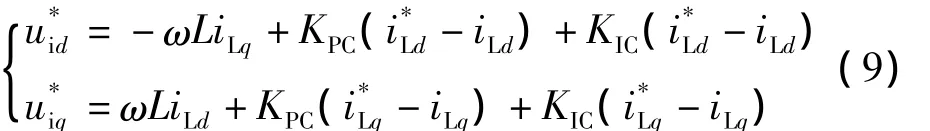
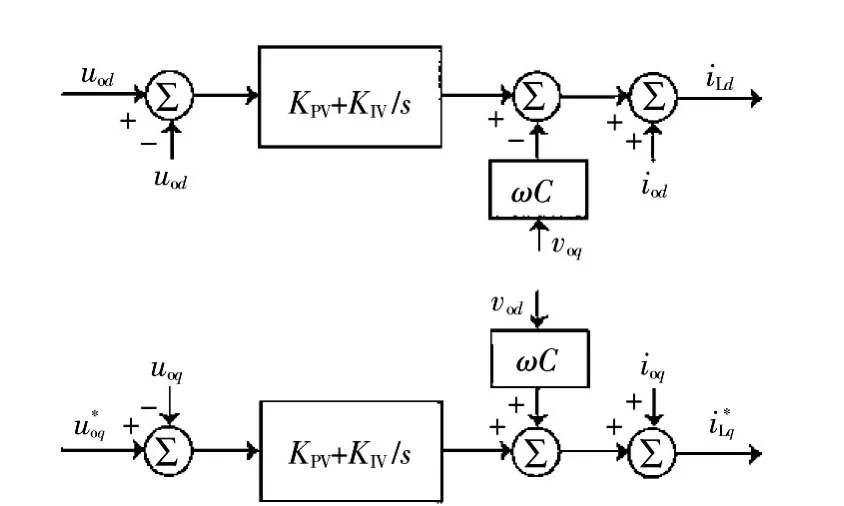
图6 电压外环控制器的结构框图Fig.6 Voltage outer loop controller structure

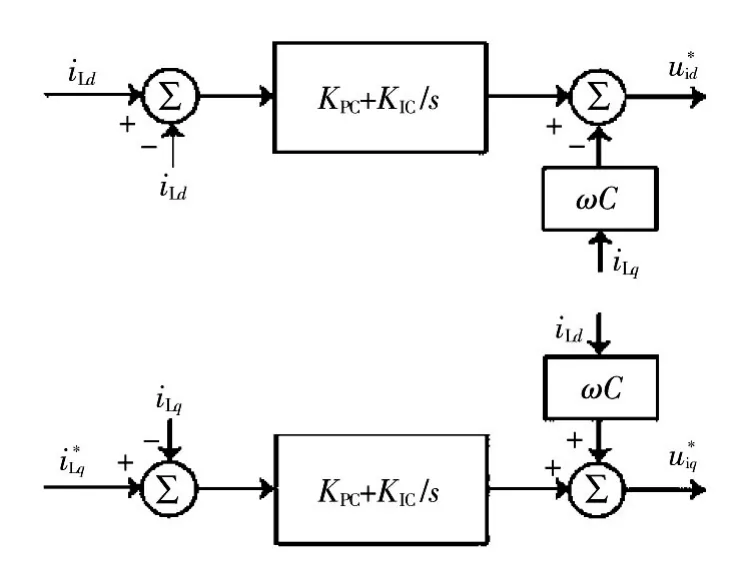
图7 电流内环控制器的结构框图Fig.7 Current inner loop controller structure

2.2 微电网的二级控制策略

在初级控制中，分布式电源通过逆变器输出的功率来控制电压和频率，但是这将会引发频率和电压的偏差。式(7)可以写成

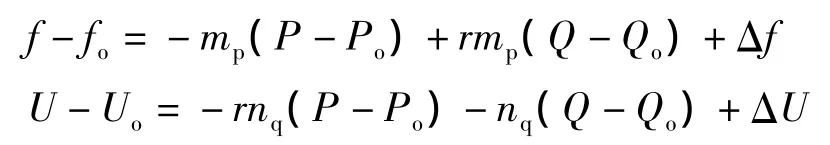
式中，Δf和ΔU分别为系统的频率偏差和电压偏差。

为了补偿这个偏差使频率和幅值重新回到额定值，引入了二级控制(Secondary control)方法。其中，频率偏差 Δf可以表示为［16］

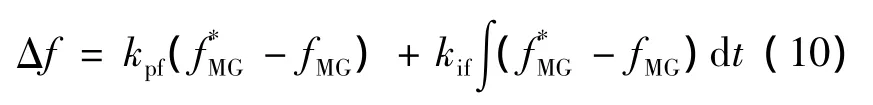
式中:kpf和kif分别为二级控制补偿器的控制参数;fMG为微电网的分布式电源输出频率;f*MG为参考值。

电压偏差ΔU可以表示为［17］

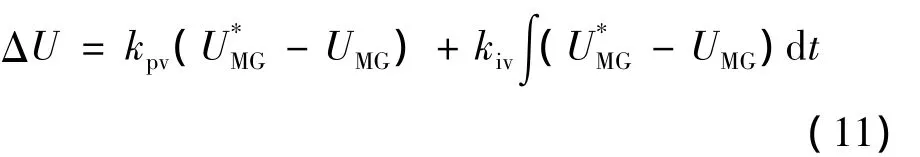
式中:kpv和kiv分别为二级控制补偿器的控制参数;UMG为微电网的分布式电源输出电压;为参考值。

从式(10)和式(11)可以看出，微电网的分布式电源输出频率fMG和电压幅值UMG与其参考值和进行比较，得到频率偏差 Δf和电压偏差ΔU。这些偏差值反馈到初级控制来控制分布式电源的控制器，进而使分布式电源的频率和电压幅值达到一个稳定值。由式(10)和式(11)可得二级控制的频率偏差和电压偏差框图，如图8所示。

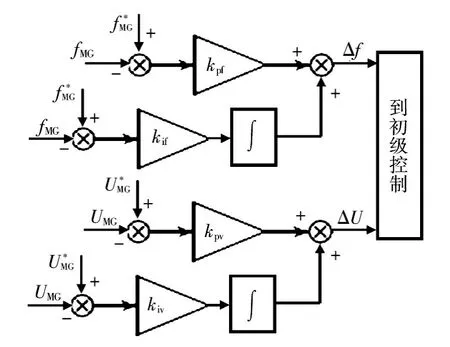
图8 二级控制的频率偏差和电压偏差框图Fig.8 Secondary control frequency deviation and voltage deviation structure diagram

3 仿真分析

为验证上述控制策略的正确性，利用Matlab/Simulink搭建仿真模型，如图9所示。

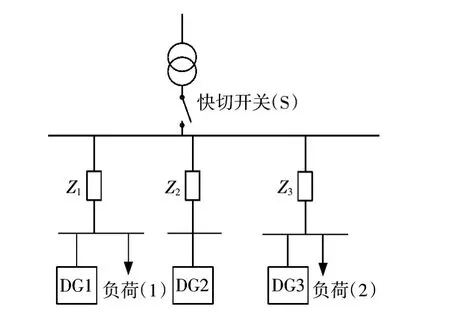
图9 系统仿真模型Fig.9 System simulation model

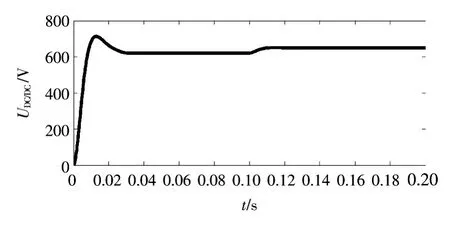
图10 DC/DC变换器输出的直流电压Fig.10 DC/DC converter output DC voltage

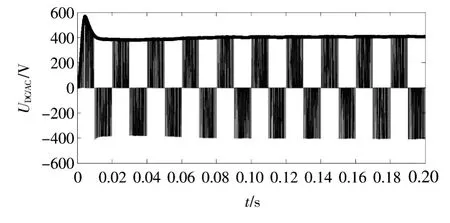
图11 DC/AC逆变器输出的交流电压Fig.11 DC/AC inverter output AC voltage

1)当初级控制(Primary control)在微电网中运行时，微电网输出的有功功率和无功功率如图12和图13所示。

图12 微电网输出的有功功率Fig.12 Micro－gird output active power

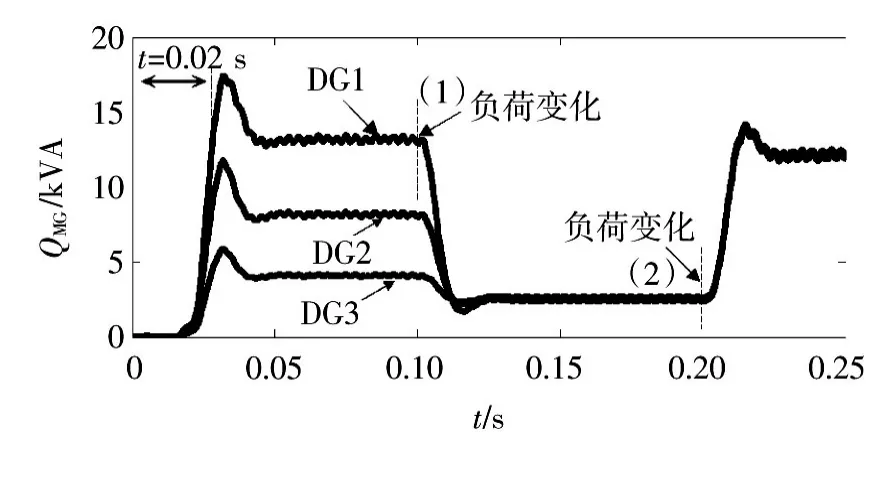
图13 微电网输出的无功功率Fig.13 Micro－gird output reactive power

由图12和图13中的仿真结果可以得出，在t=0.02 s之前，微电网的分布式电源还没有输出功率。在t=0.02 s之后，微电网输出的有功功率DG1为14 kW，DG2为10 kW，DG3为8 kW;微电网输出的无功功率 DG1为13 kVA，DG2为7.5 kVA，DG3为4.7 kVA。

频率响应如图14所示，包括微电网频率fMG、参考频率f*

MG和电网频率 fg。在 0.02 ～0.1 s，微电网输出的频率波动和电压偏差ΔU1≈45 V，如图14和图15所示。在t=0.1 s时刻后，负荷发生变化，微电网输出的有功功率和无功功率(包括DG1、DG2和DG3)分别为25 kW、2.5 kVA，如图13和14所示。在0.1～0.2 s，微电网输出的频率偏差 Δf如图14所示。同时，微电网的电压和参考电压都为380 V(UMG==380 V)，如图15所示。在t=0.2 s时刻后，负荷发生变化，微电网输出的有功功率和无功功率(包括DG1、DG2和DG3)分别为20 kW、12.5 kVA，如图13和图14所示。同时，微电网输出的电压偏差ΔU2≈12 V，如图15所示。

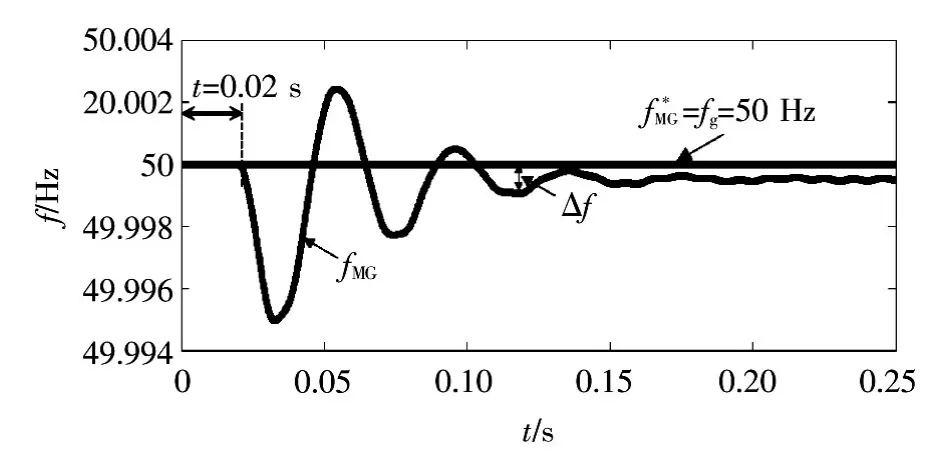
图14 频率响应Fig.14 Frequency response

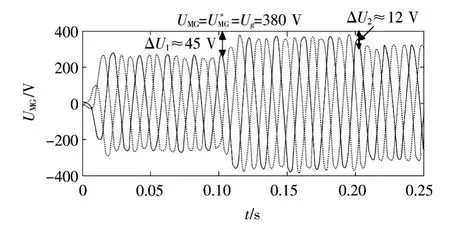
图15 微电网输出电压波形Fig.15 Micro－gird output voltage waveform

根据以上分析，在初级控制中，微电网分布式电源通过逆变器输出的功率来控制电压和频率，但是这会导致频率和电压的波动，从而导致系统不稳定。

2)当二级控制(Secondary control)在微电网中的运行时，微电网输出的电流、电压、频率和电压相角如图16—图19所示。

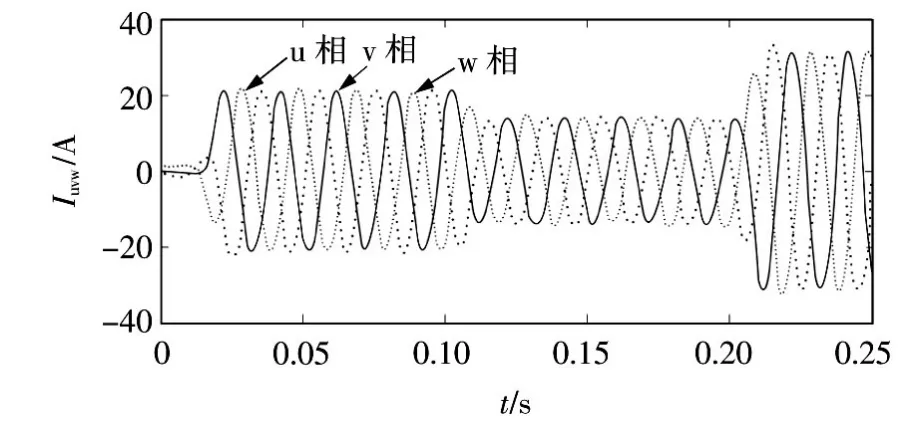
图16 微电网输出电流波形Fig.16 Micro－gird output current waveform

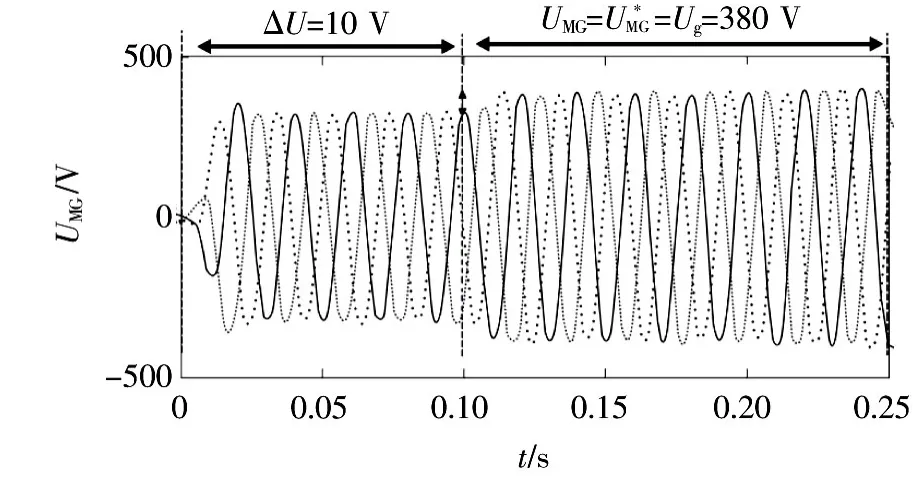
图17 微电网输出电压波形Fig.17 Micro－gird output voltage waveform

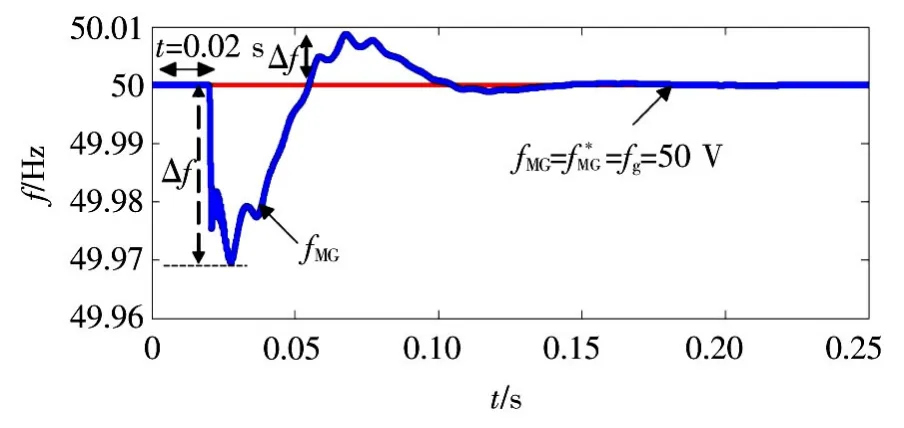
图18 频率响应Fig.18 Frequency response

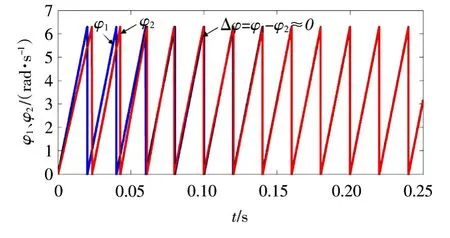
图19 微电网输出电压相角波形Fig.19 Micro－gird output voltage phase angle waveform

由图16—图19中的仿真结果可以得出，在0.02 ～0.1 s，微电网输出的频率偏差 Δf、电压偏差Δu≈10 V和电压相角偏差Δφ。根据IEEE 1547标准，对于容量为0～500 kVA的分布式电源进行并网时，允许频率偏差为0.3 Hz，电压偏差为10%，相角偏差为±20°，频率和电压的偏差不超过IEEE 1547标准所规定的允许极限，即符合该标准。在0.1～0.25 s，负荷变化(或者分布式电源出力的波动)，微电网中分布式电源的频率、参考频率和电网频率都为50 Hz=50 Hz)，微电网中分布式电源的电压、参考电压和电网电压都为380 V根据以上分析，在二级控制中，微电网中分布式电源的运行稳定，电能质量符合标准。

4 结语

本文提出的微电网分布式电源的分层控制策略不仅提高了系统供电可靠性，而且保证了微电网各种运行方式的无缝切换。在考虑到负荷变化或分布式电源出力波动性的情况下，并入电网的微电网系统频率和电压幅值一直保持稳定，频率偏差、电压偏差都在允许范围内，符合IEEE 1547标准。Matlab/simulink仿真结果表明，分层控制策略能使各分布式电源之间较好地协调，满足了系统电压和频率的要求。

［1］ 周龙华，舒杰，张先勇，等.分布式能源微网电压质量的控制策略研究［J］.电网技术，2012，36(10):18-22.ZHOU Longhua，SHU Jie，ZHANG Xianyong，et al.Control strategy of voltage quality in distributed energy microgrids［J］.Power System Technology，2012，36(10):18-22.

［2］ 孙芊，王倩，杨利萍，等.针对分布式光伏接入的配电网改造方法［J］.电力系统及其自动化学报，2014，26(5):60-65.SUN Qian，WANG Qian，YANG Liping，et al.Reconstruction method of distribution network with access of distributed photovoltaic power［J］.Proceedings of the CSU-EPSA，2014，26(5):60-65.

［3］ 韩培洁，张惠娟，李贺宝，等.微电网控制策略分析研究［J］.电网与清洁能源，2012，28(10):25-30.HAN Peijie，ZHANG Huijuan，LI Hebao，et al.Analysis and research on microgrid control strategies［J］.Power System and Clean Energy，2012，28(10):25-30.

［4］ KANCHEV H，LU D，COLAS F，et al.Energy management and operational planning of a microgrid with a PV based active generator for smart grid applications［J］.IEEE Transactions on Industrial Electronics，2011，58(10):4583-4592.

［5］ LOGENTHIRAN T，SRINIVASAN D，KHAMBADK ONE A M，et al.Multiagent system for real time operation of a microgrid in real time digital simulator［J］.IEEE Transactions on Smart Grid，2012，3(2):925-933.

［6］ TSIKALAKIS A G，HATZIARGYRIOU N D.Centralized control for optimizing microgrids operation［J］.IEEE Transactions on Energy Conversion，2008，23(1):241-248.

［7］ YAO W，CHEN M，MATAS J，et al.Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing［J］.IEEE Transactions on Industrial Electronics，2011，58(2):576-588.

［8］ PEÇAS LOPES J A，MOREIRA C L，MADUREIRA A G.Defining Control Strategies for MicroGrids Islanded Operation［J］.IEEE Transactions on Power Sysems，2006，21(2):916-924.

［9］ 李娟，周建颖，王坤.嵌套分区算法分区无功补偿提高系统稳定裕度［J］.电力自动化设备，2012，32(10):53-58.LI Juan，ZHOU Jianying，WANG Kun.NP-based sectional reactive power compensation for improving system stability margin［J］.Electric Power Automation Equipment，2012，32(10):53-58.

［10］ 黄伟，孙昶辉，吴子平，等.含分布式发电系统的微网技术研究综述［J］.电网技术，2009，33(9):14-18.HUANG Wei，SUN Changhui，WU Ziping，et al.A review on microgrid technology containing distributed generation system［J］.Power System Technology，2009，33(9):14-18.

［11］ LIU Zhen，OUYANG Shuguang，BAOWeiyu.An improved droop control based on complex virtualimpedance in medium voltage micro-grid［C］//Power and Energy Engineering Conference(APPEEC).Asia-Pacific，2013.

［12］ MAJUMDER R，CHAUDHURI B，GHOSH A，et al.Improvement of stability and load sharing in an autonomous microgrid using supplementary droop control loop［J］.IEEE Transactions on Power Systems，2010，25(2):796-808.

［13］ 艾欣，金鹏，孙英云.一种改进的微电网无功控制策略［J］.电力系统保护与控制，2013，41(7):147-155.AI Xin，JIN Peng，SUN Yingyun.An enhanced reactive sharing control strategy of microgrid［J］.Power System Protection and Control，2013，41(7):147-155.

［14］ 党克，刘旭阳，吴艳超，等.微电网孤岛运行时的频率综合控制策略的研究［J］.电力电子技术，2014，48(5):11-13.DANG Ke，LIU Xuyang，WU Yanchao，et al.Consolidated frequency control strategy of microgrid islanding operation［J］.Power Electronics，2014，48(5):11-13.

［15］ 周峰，王科，朱桂萍，等.微电网孤岛模式下全钒液流电池逆变器控制［J］.中国电力，2011，44(3):81-85.ZHOU Feng，WANG Ke，ZHU Guiping，et al.Control strategy for vanadium redox battery inverter in islanding microgrid［J］.E-lectric Power，2011，44(3):81-85.

［16］ JOSÉ GIL N，PEÇAS LOPES J A.Hierarchical frequency control scheme for islanded multi-microgrids operation［C］//IEEE Power Tech.2007:1-5.

［17］ VANDOORN T L，JEROEN D M，DE KOONING，et al.Voltage-based control of a smart transformer in a microgrid ［J］.IEEE Transactions on Industrial Electronics，2013，60(4):1291-1304.