基于单位四元数法的激光点云拼接算法研究

王英男，戴曙光

(上海理工大学 光电信息与计算机工程学院，上海 200093)

激光扫描［1］是一种典型的非接触式三维扫描测量技术，与原有工业生产中经常使用的接触式测量相比，具有测量精度高、测量效率高、操作简单等优点，被广泛应用于汽车工业、模具器件测量、质量检测、文物保护等领域。但是由于激光扫描技术是利用被测工件，将激光源所发射的激光线通过漫反射反射到固定的图像传感器上成像，从而计算出被测工件空间坐标，因此，易受到被测工件表面颜色、粗糙度、外形等因素的影响。为解决此问题，在实际应用中需要对被测工件的某些特殊部分单独以适宜姿态进行扫描，而后通过坐标转换将两片点云统一到同一坐标系下完成点云拼接得到完整的扫描结果。

1 常用坐标转换方法

各坐标系之间的坐标转换主要有三参数，四元数，七参数3 种方法，其中三参数法可以视为是七参数方法的一种特例。

七参数法采用布尔莎模型［2］进行求解，该模型需要求得3 个平移量Δx，Δy，Δz，3 个旋转量α，β，γ 和1个尺度参数变化K 共7 个参数，其转换公式［3］如下

从而可得

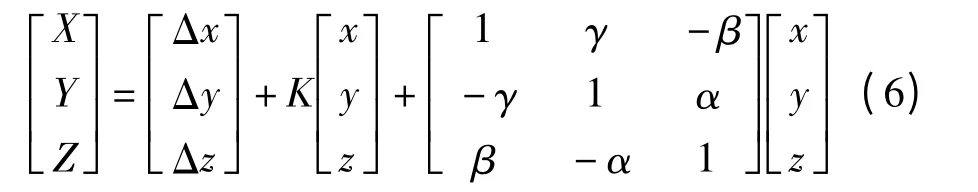
其中，Δx，Δy，Δz 是3 个平移参数;α、β、γ 是3 个旋转参数;K 是尺度参数;x、y、z 是转换前坐标;X、Y、Z 为转换后所得坐标。

由式(6)可知，如果7 个参数已知，可用七参数法实现坐标转换，然而实际应用7 个参数是未知的，求得七参数需要在同一地区至少存在3 个重合点，即至少3 个点在两个坐标系中的坐标均已知，才可通过最小二乘法拟合来求取［4］，然而此方法计算复杂且在旋转角度过大时会有较大误差，而基于四元数的坐标转换可以有效地弥补这个问题，因此本文使用四元数方法来实现激光器的坐标转换。

2 基于单位四元数的坐标转换方法

四元数于1843 年由哈密顿提出，是一种简单的超复数，由一个实数单位和3 个虚数单位构成。点云配准的过程是将激光在不同站点以不同姿态所采集的点云统一到同一坐标系下的过程，即其目标是为了寻找最小二乘逼近的坐标转换矩阵［5］，坐标转换矩阵可由一个平移矩阵和一个旋转矩阵构成。单位四元数法的使用必须满足两片点云中具有重叠部分，即两片点云中有点集A，B 并满足以下条件［6］:(1)A 中点的个数和B 中点的个数相等，即两个点集具有相同数量的点NA=NB=n。(2)A 中的每个点Ai与B 中相同下标的点Bi相等，即Ai=Bi。

设旋转变换向量为单位四元数qR=［q0q1q2q3］T，其中q0＞0，且从而可以求得3×3 的旋转矩阵R(qR)。设平移向量为qT=［q4q5q6］T，可得到坐标变换向量为则求最佳变换向量可转换为求q，使得函数

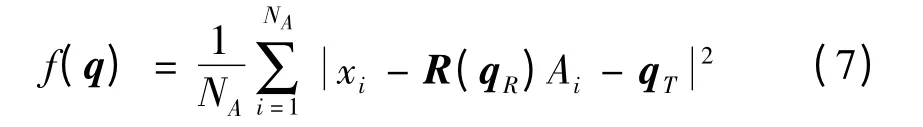
最小化。式中矩阵R(qR)为点云旋转矩阵，算法过程［7］如下:

(1)分别计算计算出两片点云的重心。参考点云重心为

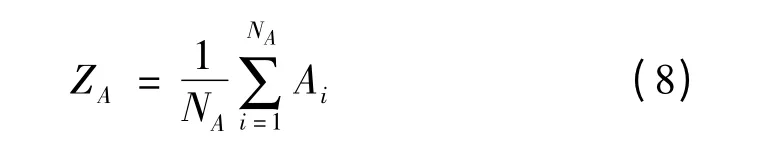
目标点云重心为

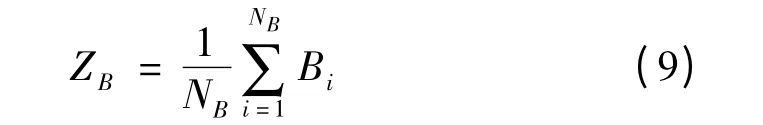
(2)由点云AB 求得协方差矩阵为

由协方差矩阵构成的4×4 对称矩阵

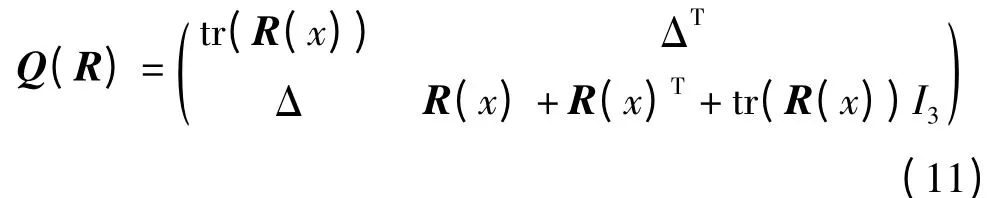
其中，tr(R(x))为矩阵R(x)的迹;I3为3×3 的单位矩阵

(3)计算4×4 矩阵Q(R)的特征值与特征向量，其最大特征值对应的特向量即为最佳旋转的单位四元数［q0q1q2q3］T，则可计算出旋转矩阵为

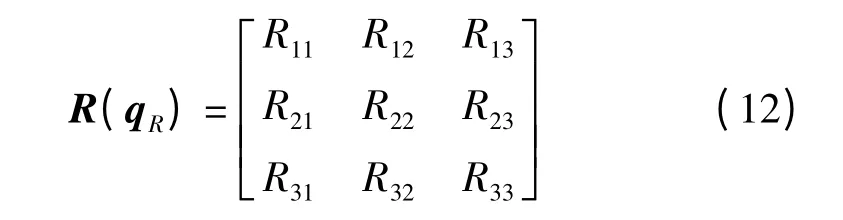
(4)计算平移矩阵为

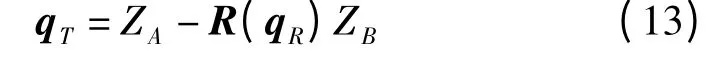
3 实验结果

为验证上述方法的拼接效果，本文通过计算机模拟，使用激光器对鼠标进行垂直方向扫描，扫描结果通过Matlab 仿真结果如图1 和图2 所示。

图1 鼠标整体扫描初始图

图2 鼠标左半边缘扫描图

如图1 所示，由于鼠标为黑色且左右边缘形状不规则，激光线在垂直照射其边缘时反射效果较差，因此在激光器图像传感器中无法成像也无法取得其空间坐标信息，激光器反馈为无效数据(－294.912)，因此其显示为深蓝色，为得到鼠标边缘轮廓数据，使用激光器以适宜角度，对其左边缘进行单独扫描，结果如图2 所示。将图2 所采集点云与图1 所采点云进行拼接即可得到完整鼠标点云，算法流程如图3 所示。

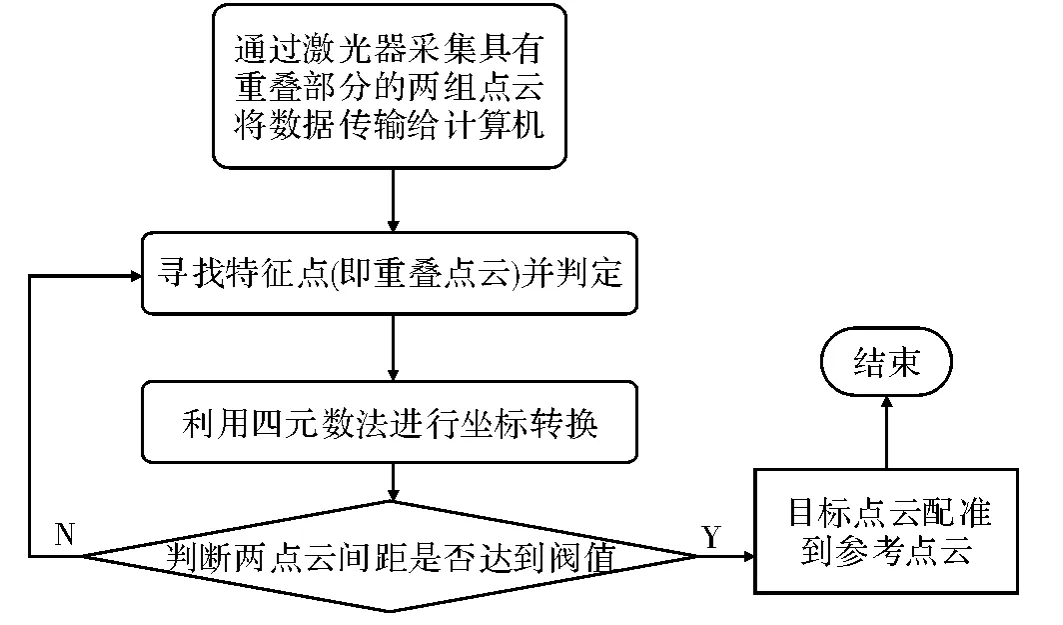
图3 点云拼接算法流程图

图4 为初始数据输入，经过多次迭代后其输出结果如图5 所示。

图4 拼接前鼠标原始图

图5 拼接完成后效果图

由图5 与图1 比较可明显看出鼠标左边边缘拼接效果良好，由鼠标旁边的光学检测台检测孔的重叠状态可知此方法具有良好的配准精度。

4 结束语

随着激光传感器在工业生产中的广泛应用，基于激光扫描的点云配准技术倍受业界关注。本文提出了一种基于单位四元数的点云配准算法，与传统七参数，三参数等算法相比，在配准速度与精度上具有明显优势，同时实验结果表明，该算法可实现点云自动化识别与拼接且结果正确，可以使激光器对同一物体具有重叠部分的不同部位以不同姿态进行扫描，对扫描结果进行点云拼接，从而得到被测物完整的空间扫描信息，大幅提高了激光器在生产中的实用性。

［1］ 刘旭春，丁延辉.三维激光扫描技术在古建筑保护中的应用［J］.测绘工程，2006(1):48－49.

［2］ 王解先，邱杨媛.高程误差对七参数转换的影响［J］.大地测量与地球动力学，2007，27(3):266－268.

［3］ 李金岭，刘鹂，乔书波，等.关于三维直角坐标七参数转换模型求解的讨论［J］.测绘科学，2010(4):76－78.

［4］ 茹树青，吉长东，王宏宇.坐标转换中四参数法与七参数法精度比较［J］.东北水利水电，2006(5):67－68.

［5］ 杨帆，李广云，王力，等.一种基于罗德里格矩阵的最小二乘迭代坐标转换方法［J］.工程勘察，2010(9):80－84.

［6］ 戴静兰，陈志杨，叶修梓.ICP 算法在点云配准中的应用［J］.中国图像图形学报，2007，12(3):517－521.

［7］ Besl P J，McKay H D.A method for registration of 3－d shapes［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14(2):239－256.