基于1stOpt软件的树高测量模型1)

郭欣雨 冯仲科 曹忠 范永祥

(精准林业北京市重点实验室(北京林业大学)，北京，100083)

责任编辑:王广建。

在林业资源调查中，树高是最重要的林木因子和衡量林分生长的重要指标［1］。树高测量模型在林木生长模型构建、立地质量评估等方面具有重要的作用［2］，快速、精准、简便的树高模型拟合方法对林业工作具有重要意义。

随着计算机科技的发展，通常使用SPSS、SAS、MATLAB等软件对树高模型进行拟合，拟合精度得到大幅度提高［3］。近年来，陈丽聪等［4］、刘平等［5］采用SPSS软件中最小二乘法，对不同起源树种以及多种树高模型进行了曲线拟合，并做出了对比;王霓虹等［6］采用MATLAB软件拟合落叶松的树高生长模型求解参数;王庆丰等［7］使用SAS拟合林分的差分模型。但是在运用上述软件时，需要进行初始化，算法操作较为复杂。

为了满足现代林业技术发展的需求，更加快速、简便、精确地拟合树高模型，尝试利用1stOpt软件中所使用的麦特夸(LM)+通用全局优化算法(UGO)对树高模型进行曲线拟合并估算其参数。将其结果与现代林业调查中最为常用的SPSS软件的普通最小二乘法拟合结果进行对比与评价。

对于树高模型，诸多学者在比较与选择上做了大量研究。Huang S等［8］系统比较了33个曲线模型与非曲线模型;王明亮等［9］则通过失拟检验的理论和方法对非线性树高曲线模型的适度进行了检验，表明3参数模型描述树高曲线表现良好;范金阜［10］运用树高抛物线模型(H=a0d2+a1d+a2，其中:H为树高，d为胸径，a0、a1、a2为参数)对落叶松树高建模取得良好的拟合效果。因此，本试验在树高模型的选择上，采用了经典的测量树高的抛物线模型。在进行模型评价和比较时，曾伟生等［11］、Kozak［12］提出应当将检验样本与建模样本合并进行建模，避免建模时的样本总量损失，因此，本研究不再预留样本数据进行适用性检验。

1 研究区概况

研究地选择内蒙古喀喇沁旗旺业甸实验林场，该林场位于赤峰市喀喇沁旗西南部，地理坐标为东经118°09'～118°30'，北纬41°21'～41°39'。林场属温带季风气候区，气温变化剧烈，全年日照时间2 700～2 900 h。主要地貌为中山和低山山地，地形起伏不平，山脉相连，沟谷纵横，海拔800～1 890 m。土壤类型多样，有棕壤、褐土、草甸土和山地黑土，以典型棕壤为主。林场有林地面积为23 118 hm2，林场活立木总蓄积量1 255 756 m3。森林植被主要有油松(Pinus tabulaeformis)、落叶松(Larix gmelinii)、山杨(Populus)、白桦(Betula platyphylla)、蒙古栎(Quercus mongolica)等。

2 研究方法

2．1 数据来源

在旺业甸实验林场标准样地，利用电子经纬仪测得181株落叶松立木实测数据。剔除有明显误差的数据后，将全部样木数据作为建模样本，按照胸径、树高、材积进行统计，样木数据基本情况统计如表1所示。

表1 样木数据基本情况统计

2．2 Levenberg－Marquarat+通用全局优化算法(LMUGO)

LM－UGO算法具有强大的容错、寻优功能。该算法最大特点是克服了使用迭代法必须给出合适初始值的难题，终端用户无需给出其参数初始值，而是由1stOpt自身随机给出，通过其独特的全局优化算法，最终得出最优解。普通最小二乘法优化的最终目标是从某个初始点开始，确定一个搜索方向并在该方向上做一维搜索，当找到可接受点之后，再通过一定的策略调整搜索方向，并继续在新的方向上进行一维搜索，依此类推，直到目标函数已经收敛到了极小值点。

信赖域算法是不通过调整搜索方向→进行一维搜索的步骤，也能求得极小值点。信赖域和一维搜索同为最优化算法的基础算法，信赖域算法是没有一维搜索过程的。信赖域算法的数学模型为:

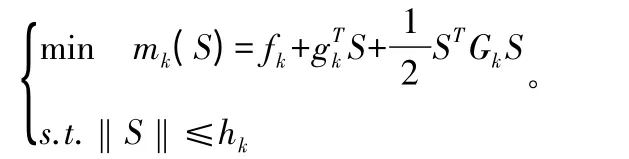
当信赖域模型中的范数‖S‖≤hk取2范数时，得到LM－UGO算法的数学模型:

2．3 1stOpt(LM－UGO)法

1stOpt是七维高科有限公司开发的数学优化分析综合工具软件包。其计算平台具有操作简便、运行稳定、功能强大，操作界面简洁易懂的特点［13］。它所使用的通用全局优化算(LM－UGO)，具有强大的容错、寻优功能，在非线性拟合，参数估算等优化领域独树一帜。该算法之最大特点是克服了当今世界上在优化计算领域中使用迭代法必须给出合适初始值的难题，终端用户无需给出其参数初始值，而是由1stOpt自身随机给出，通过其独特的全局优化算法，最终得出最优解。

2．4 SPSS软件的最小二乘法

SPSS软件作为集数据处理、图表编辑、统计分析以及数据接口于一体的大型通用专业统计分析软件，具备强大的频数分布分析、相关分析、回归分析等功能［14］。而普通最小二乘法是线性回归模型最重要的参数估计方法之一［15］。因此，利用SPSS软件的普通最小二乘法对树高模型H=a0d2+a1d+a2进行拟合。

2．5 基本评价指标

综合考虑各种因素，现将确定系数(R2)、估计值的标准误差(SEE)、总相对误差(TRE)、平均系统误差(MSE)、平均预估误差(MPE)、平均百分标准误差(MPSE)、参数稳定性指标和残差随机性等指标作为基本评价指标。

决定系数(R2)即拟合指数，表示在因变量的总平方和中，由自变量引起的平方和所占的比例。当R2越接近1时，表示相关的方程式参考价值越高;相反，越接近0时，表示参考价值越低。

标准误差(SEE)是由于在测量过程中待测物体的真值难以获取，在实际的计算中，一般用标准误差估算值代替实际误差。

相对误差(TRE)是指测量所造成的绝对误差与被测量真值之比。一般来说，相对误差更能反映测量的可信程度。

平均相对误差(MSE)是相对误差的平均值，通常用平均相对误差绝对值表示。

平均预估误差(MPE)是反映平均树高估计值的精度指标。

平均百分标准误差(MPSE)，是反映单株树高估计值的精度指标。

具体公式如下:

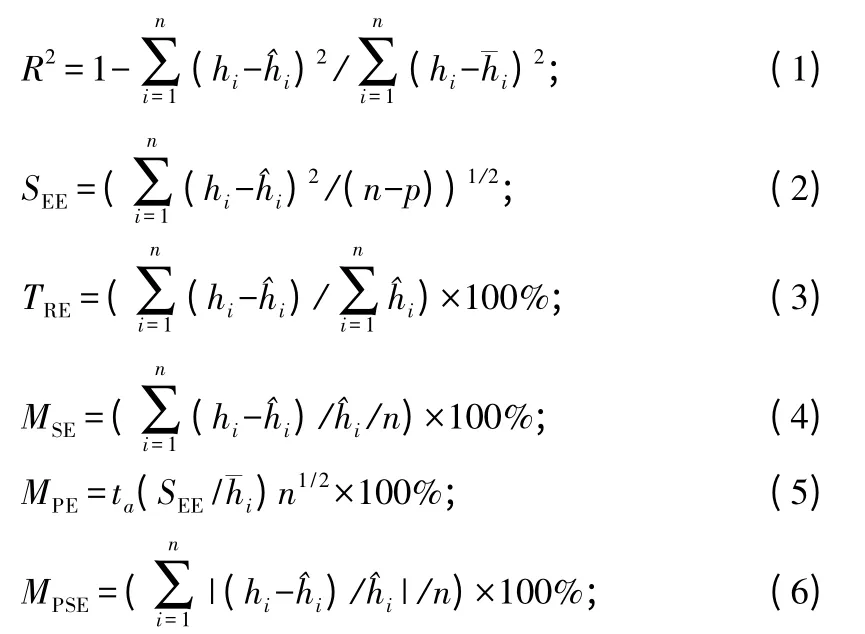
式中:hi为样木的实测值，^hi为样木的估算值，n为样本单元数，p为参数个数，ta为置信水平a时的t值，CV为变动系数。

R2和SEE是回归模型最常用的指标，反映了模型的拟合优度;TRE和MSE是反映拟合效果的重要指标，二者都应该控制在(－3%，3%)或(－5%，5%)的范围内，指标值越趋于0，效果越好;MPE是反映平均树高估计值的精度指标;MPSE是反映单株树高估计值的精度指标;CV是描述参数稳定性的重要指标，它的值应小于50%［16］。

另外，残差的随机性用以描述残差分布是随机的，各个径阶的残差应当正负相抵。若以0残差作为基准线，上下对称分布，则残差分布为随机。

2．6 方程适用性检验

由两个不同拟合方法获得的模型是否合格，还需要进行适用性检验，设y为实测树高，x为模型估算树高，使用直线方程y=bx+a进行线性回归，a值越是接近1，b值越是接近0，则方程拟合程度越好。

为检验所选树高模型是否适应，必须对y与x之间线性关系的显著性进行F检验。通过a、b可以以求得一个F值，通过样本数及方程的自由度可以查表得到允许F值，若实得F值大于允许值，则从数量上说明了其合理性。F值越高，说明其线性关系的显著性越高，计算得出F值后，通过其自由度a(n1，n2)及位置水平查得Fa(n1，n2)。若F＞Fa(n1，n2)，则满足要求。即:

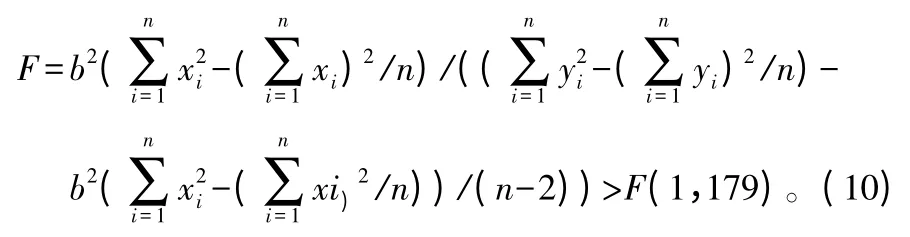
3 结果与分析

3．1 LM－UGO法树高模型拟合结果

在1stOpt中软件中，利用麦特夸(Levenberg－Marquarat－LM)+通用全局优化算法(Universal Global Optimization－UGO)对树高模型H=a0d2+a1d+a2进行曲线拟合。

编写程序代码如下:

Title"基于1stopt的树高模型拟合";

(数据部分省略)

算法设置为Levenberg－Marquardt法(LM)+通用全局优化算法(UGO)，其余参数选择默认值。

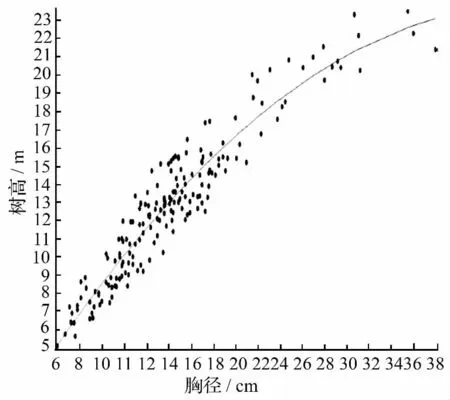
图1 1stOpt树高模型拟合结果点线图

3．2 SPSS软件普通最小二乘法树高模型拟合结果

打开SPSS软件，将树高及胸径数据导入，将抛物线公式输入并将算法设置为普通最小二乘法，选择默认收敛条件进行拟合，从而得到树高与胸径关系的点线图(见图2)。

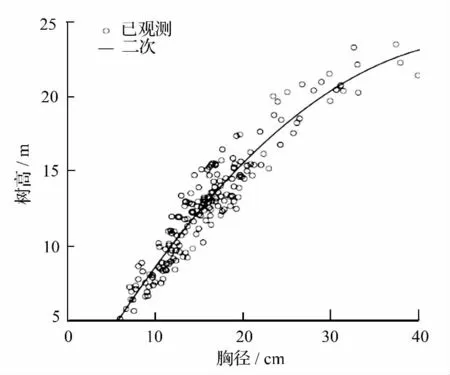
图2 SPSS软件普通最小二乘法树高模型拟合结果点线图

3．3 LM－UGO法与普通最小二乘法树高模型拟合结果比较

分别使用1stOpt中LM－UGO算法与SPSS软件中最小二乘法对树高模型进行拟合，拟合结果见表2。

表2 两种方法对树高模型的拟合结果

将胸径分别带入LM－UGO及SPSS所建模型，得到树高估计值(^h)，结合树高实测值(H)，运用公式(1)～(7)进行计算，得到各项评价指标(见表3)。由表3可知，LM－UGO算法与SPSS的最小二乘法对树高模型的拟合均取得了较好的结果。其确定系数(R2)均超过0．90，说明胸径因子已经解释了树高因子变动的90%以上，且LM－UGO拟合结果优于SPSS最小二乘法所得结果。估计值的标准差(SEE)分别为1．208 4和1．223 7;平均系统误差(MSE)、总相对误差(TRE)分别为都在(－3%，3%)的范围内，在这两项体现拟合效果的重要指标中，LMUGO较SPSS最小二乘法所得拟合值更趋近于0，即LM－UGO拟合效果更优;平均预估误差(MPE)中置信水平a取0．05(t0．05=1．960)时，MPE在3%以内，平均百分标准误差(MPSE)约为8%，LM－UGO同样优于SPSS最小二乘法;变动参数(CV)值，CVLM－UGO＜CVSPSS最小二乘法＜50%。从基本评价指标来看，LMUGO算法明显优于SPSS最小二乘法拟合结果。

表3 树高模型拟合参数估计值及统计指标

分别基于1stOpt软件和SPSS最小二乘法的得到残差柱状图和残差散点图(见图3、图4)。两图均显示出在零残差线上下基本对称，即残差随机项均合格。

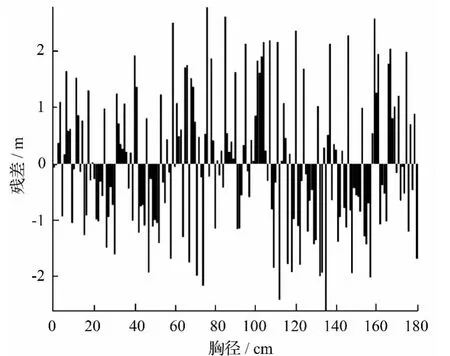
图3 基于1stOpt软件的残差柱状图

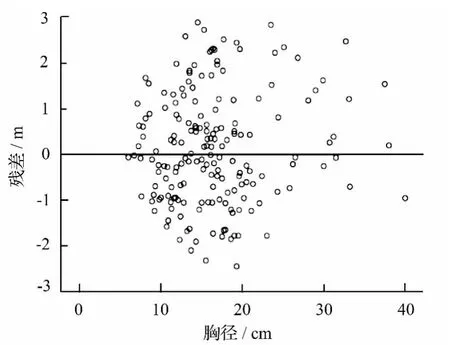
图4 基于SPSS软件的残差散点图

综合以上8项评价指标可以得出，LM－UGO所获取的拟合模型在各个精度上均优于SPSS软件最小二乘法。

3．4 方程适用性检验结果

通过实测树高与模型所得树高线性回归得到a、b值。通过实验数据获取到模型自由度为(1，179)，置 信 水 平a=0．05，查 表 得t0．05=1．960，F0．05(1，179)=2．924。检验结果如表4所示。

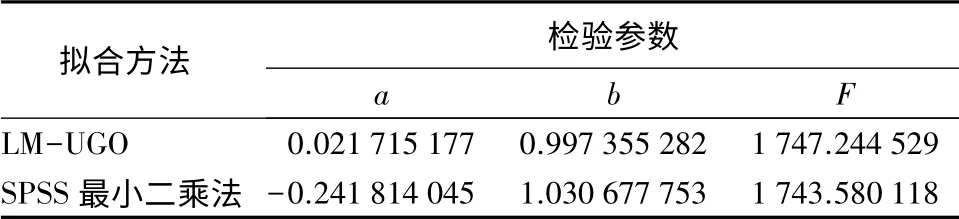
表4 两种方法计算结果的检验

通过表4可以看出，F检验结果，FLM－UGO＞FSPSS最小二乘法＞F0．05(1，179)，故LM－UGO法所得树高与实测树高线性显著性更高。并且LM－UGO所得a、b值较于最小二乘法更分别接近于1和0，说明LMUGO法拟合程度更好。

4 结束语

1stOpt软件独特的通用全局优化算法，如今已经被广泛应用于非线性回归、非线性复杂模型参数估算求解，并在农业工程、坏境科学、社会经济等领域得到验证。LM－UGO所具有的不依赖初始值的特性对树高模型进行拟合，与常用的SPSS软件中的最小二乘法相比较，不仅大大降低了终端用户的操作难度，还有效提高了求解的成功率。使用LMUGO法拟合所得的树高模型，在林分材积表、出材量预测、经济评价和林分蓄积量计算等方面起到进一步的推动作用。

［1］陈立莉．树种树高曲线模型的研究［D］．哈尔滨:东北林业大学，2013．

［2］王璞，马履一，段劼，等．华北落叶松林平均木－优势木树高模型的研究［J］．安徽农业科学，2013，41(21):8963－8964．

［3］杜婧，冯仲科，樊潇飞，等．基于1stOpt软件的二元立木材积方程的研究［J］．中南林业科技大学学报，2014，34(4):64－67．

［4］陈丽聪，邓华锋，黄国胜，等．不同起源马尾松与杉木林分树高曲线的拟合及对比［J］．西北农林科技大学学报:自然科学版，2014，42(1):57－64．

［5］刘平，马履一，贾黎明，等．油松人工林单木树高生长模型研究［J］．林业资源管理，2008(5):50－56．

［6］王霓虹，王志芳．孟家岗落叶松人工林标准树高模型的研究［J］．森林工程，2014，30(2):10－12．

［7］王庆丰，倪成才，骆国民．用SAS的mixed过程拟合林分的线性差分生长模型［J］．科技致富向导，2013(35):108－109．

［8］Huang S，Titus S．IComparison of nonlinear height-diameter function for major AIbera tree species［J］．Can J For Res，1992，22(9):1297－1304．

［9］王明亮，李希菲．非线性树高曲线模型的研究［J］．林业科学研究，2000，13(1):75－79．

［10］范金阜．关于树高方程的选配［J］．林业资源管理，1981(1):18－21．

［11］曾伟生．全国立木生物量方程建模方法研究［D］．北京:中国林业科学研究院，2011．

［12］Kozak A，Kozak R．Does cross validation provide additional information in the evaluation of regression models［J］．Can J for Res，2003，33(6):976－987．

［13］Cheng Xianyun，Chai Fuxin，Gao Jing，et al．1stOpt and Global Optimization Platform:Comparison and Case Study［C］//Proceedings of 2011 4th IEEE International Conference on Computer Science and Information Technology．Beijing:IEEE，2011．

［14］琚松苗．SPSS在林业生产和科学研究中的应用实例解析［J］．安徽林业科技，2011，38(1):28－30．

［15］刘明．普通最小二乘法的几何分析［J］．统计与决策，2012(4):90－92．

［16］曾伟生，张会儒，唐守正．立木生物量建模方法［M］．北京:中国林业出版社，2011．