半波长交流输电线路电容调谐分析

马立新，费少帅，穆清伦

（上海理工大学光电信息与计算机工程学院，上海200093）

我国能源资源和负荷需求呈逆向分布格局，决定了我国必须在超远距离输电技术上寻求新的突破[1]。但西部能源供给中心与东部能源需求中心之间距离达2 000～3 000 km，所以我国急需超远距离、超大容量的电力输送技术，而半波长交流输电技术以其显著的经济和技术优势，在超远距离点对点输电模式中具有竞争力和应用前景[2-4]。

半波长交流输电技术HWACT（half-wavelength AC transmission）是输电的电气距离接近1 个工频半波，即3 000 km（50 Hz）或2 500 km（60 Hz）时的超远距离三相交流输电技术[3-8]。根据传输线理论，均匀无损的半波长传输线的首端和末端具有相同的电压幅值和输入阻抗，且首末电压的稳定性极好，可利用半波长交流输电的这些优势来实现超远距离点对点交流输电[5-6]。全线无需设置开关站，无需安装无功补偿装置，线路输电能力很强。

值得注意的是，实际工程中建造正好满足自然半波长度的线路是难以实现的[9-10]。当输电线路长度不足半波长时，需要对线路进行人工调谐，以达到人工半波输电线路的目的[13-16]。由基于传输线理论模型的T 型、π 型、均匀电容型人工调谐网络的比较得出，电容型调谐方式具有输电线路的沿线过电压水平较低、功率传输能力更强、系统的暂态稳定性好等优点[14]，但由于需要调谐电容均匀分布在输电线路上，输电的经济性较差，且具体不同数量的调谐电容对输电效果的相关分析数据不足[7]。

本文基于电容型调谐电路，推导出调谐电容值的计算公式，并结合某1 000 kV 交流输电线路，对调谐后的效果进行计算分析。

1 理论模型与电容计算

假设某均匀有损传输线的单位长度电阻、电感、电导及电容分别为R0、L0、G0和C0，则传输线的单位阻抗Z0和单位导纳Y0分别为

由此得到有损传输线的输电线路的特性阻抗Zc与传播常数γ 分别为

线路的电气半波长为

均匀电容型调谐电路模型如图1 所示，传输线长度为L。

图1 均匀电容型调谐电路模型Fig.1 Uniform capacitance tuning circuit model

由于输电线路属于低损耗的传输线范畴，输电线路单位长度电抗ωL0远远大于单位长度电阻R0，单位长度电纳ωC0远远大于单位长度电导G0[11-12]。那么

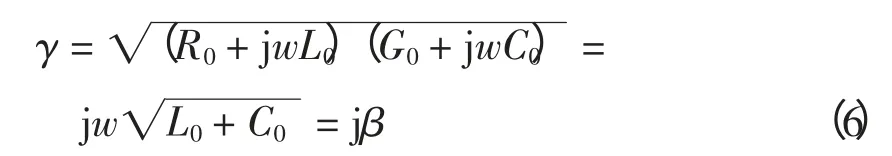
如果每间隔单位长度放置1 个调谐电容，不难计算出单位调谐电容值为

当输电频率为50 Hz 时，有

设传输线的调谐电容数为N，则相邻调谐点之间的距离为L/N，计算得到调谐电容值CN为

由式（9）可以看出，均匀电容型调谐电路的电容值与传输线的调谐电容数成反比。

2 算例与仿真分析

结合某1 000 kV 交流输电线路，分析电容型调谐电路的调谐效果及调谐效果趋于稳定时的最少调谐电容数。该输电线路正序分量的单位长度电阻、电感、电导及电容分别为R0=0.007 92 Ω/km、L0=0.835 243 mH/km、G0=0.000 2×10-5S/km、C0=0.013 738 μF/km。根据数据可算出输电线路的单位长阻抗Z0=（0.007 92+j0.262 4）Ω/km，线路单位长导纳Y0=（0.000 2+j0.431 6）×10-5S/km。基于以上数据，根据λ/2=π/β，计算出传输线路的半个波长实际为2 951.8 km，比理论值3 000 km 略短，这是由线路的损耗引起的[14]。

以2 400 km 输电线路为例分析均匀电容型调谐方式。由于输电线路2 400 km 小于实际电气半波长2 951.8 km，用电容型调谐方式将2 400 km 输电线路的电气波长调谐成2 951.8 km，使其满足半波长输电的要求。根据传输线路参数与调谐电容值的计算公式，可以计算出单位调谐电容C1=7.047 6 pF，则输电线路的调谐电容值与调谐电容数之间的关系如图2 所示。

图2 电容值与调谐电容数的关系Fig.2 Relationship between capacitance value and number of tuning capacitances

当线路距离不等于半个工频波长，即不满足半波长输电的要求时，须对线路进行调谐。调谐前后的电压波形如图3 所示。由图可以看出，调谐前，输电线路电压波形已经不满足输电要求，过电压严重，并且传输功率越大，波形变化越严重，所以超远距离输电和短距离输电特性有很大区别；采用均匀电容调谐后，线路电压保持正常，由此也证明了本文推导出的基于无损传输线的调谐电容计算公式同样适用于低损耗类型的实际输电线路。

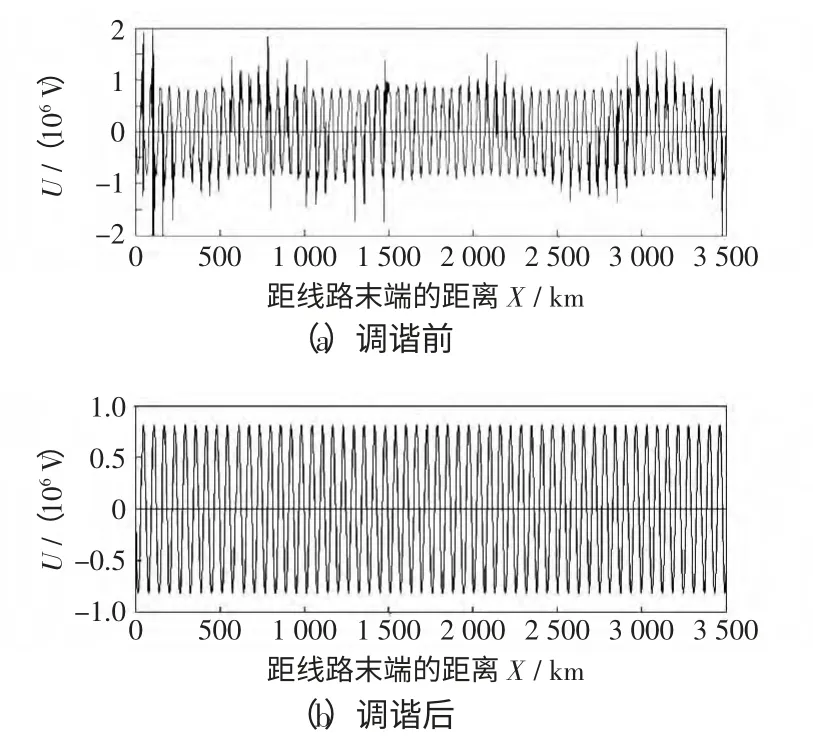
图3 调谐前后的电压波形Fig.3 Voltage waveforms before and after tuning

图4为经电容调谐后的线路传输功率P=SIL、P=1.5SIL、P=2.0SIL 时的沿线电压波形（SIL 为自然功率，功率因数为1）。由图4 可以看出经过电容调谐后，传输2 倍的自然功率时线路沿线电压最大值为1.5 p.u.；从过电压水平上，电容型调谐线路的过电压较低，且线路两端的电压增加较小。

图4 均匀电容型调谐线路的沿线电压Fig.4 Voltage along line of uniform capacitance tuning network

线路传输功率对首末电压比的影响如图5 所示。由图5 可以看出，电容调谐前的2 400 km 输电线路的首末电压比U1/UL受输电功率P 的影响很大；采取电容调谐措施后，可以看出调谐后的曲线与半波长线路曲线基本一致。

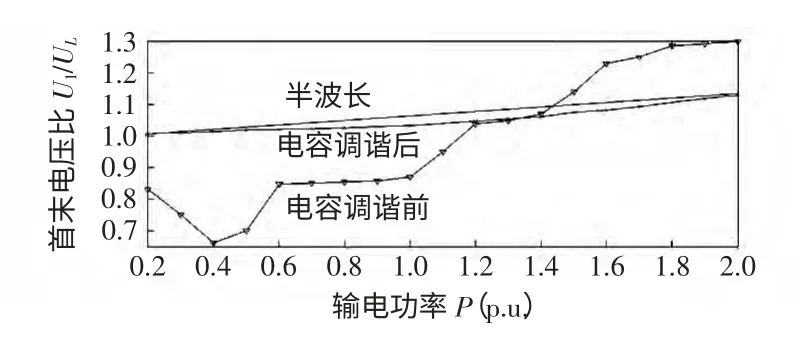
图5 线路传输功率对首末电压比的影响Fig.5 Influence of transmission power to voltage ratio

调谐电容数N 对U1/UL调谐效果的影响如图6 所示，其中，受端功率为1 倍的自然功率，功率因数分别为1.0 和0.8。由图5 可以看出，当线路调谐电容数超过8 时，无论是功率因数为1.0 或0.8，调谐效果基本趋于稳定，由此可知保持调谐效果的最少调谐电容数。

图6 调谐电容数对调谐效果的影响Fig.6 Influence of capacitance number to tuning effect

3 结语

采用半波长交流输电方式时，当实际线路长度不足半波长时，输电线路不满足半波长输电特性，对线路采取均匀电容型调谐可以达到人工半波长输电的目的。从文中分析可看出电容型调谐线路的沿线过电压水平相对较低，绝缘设计容易实现且传输功率大，证明了电容调谐的可行性。电容调谐时，在线路长度固定的情况下，调谐电容值与调谐电容数目成反比；而且对线路均分8 段调谐后，调谐效果基本趋于稳定且达到半波长交流输电的目的，对实际工程实施和投资评估具有重要的理论指导意义。

[1]吴敬儒（Wu Jingru）. 中国电网的发展与改革展望（Proospects of development and renovation of power systems in China）[J]. 电网技术（Power System Technology），2001，25（11）：6-9.

[2]王仲鸿（Wang Zhonghong）. 交流特高压在中国应用的经济和安全分析研究（Economy and security analysis of AC UHV in China）[J]. 电力自动化设备（Electric Power Automation Equipment），2007，27（10）：1-4.

[3]周浩，钟一俊（Zhou Hao，Zhong Yijun）. 特高压交、直流输电的适用场合及其技术比较（Applicable occasions of UHVAC/UHVDC transmission and their technology comparisons in China）[J]. 电力自动化设备（Electric Power Automation Equipment），2007，27（5）：6-12，39.

[4]邓键超. 智能电力设备与半波长交流输电[C]//中国电机工程学会第九次全国会员代表大会学术报告会. 北京，中国：2009.

[5]孙珂（Sun Ke）. 特高压半波长交流输电经济性分析（Economic analysis on UHV half-wavelength AC power transmission）[J].电网技术（Power System Technology），2011，35（9）：51-54.

[6]邓键超（Deng Jianchao）.关于我国交流输电更高一级电压的选择（On the alternatives for the next voltage level of AC power transmission）[J]. 电网技术（Power System Technology），1995，19（1）：3-8.

[7]周厚奎， 张昱， 金心宇 （Zhou Houkui，Zhang Yu，Jin Xinyu）. 基于傅里叶和小波变换的电网谐波分析（Power harmonic analysis based on Fourier and wavelet transform）[J]. 电力系统及其自动化学报 （Proceedings of the CSU-EPSA），2005，17（6）：59-62，99.

[8]Hubert G J，Gent M R. Half-wavelength power transmission lines[J]. IEEE Trans on Power Apparatus and Systems，1965，84（10）：965-974.

[9]Prabhakara F S，Parthasarathy K，Ramachandra Rao H N.Analysis of natural half-wave-length power transmission lines[J]. IEEE Trans on Power Apparatus and Systems，1969，88（12）：1787-1794.

[10]Lliceto F，Cinieri E. Analysis of half-wave length transmission lines with simulation of corona losses[J]. IEEE Trans on Power Delivery，1988，3（4）：2081-2091.

[11]Prabhakara F S，Parthasarathy K，Ramachandra Rao H N.Performance of tuned half-wave-length power transmission lines [J]. IEEE Trans on Power Apparatus and Systems，1969，88（12）：1795-1801.

[12]Gatta F M，Lliceto F.Analysis of some operation problems of half-wave length power transmission lines[C]//IEEE Africon Conference，Ezulwini Valley，Swaziland：1992.

[13]Kimbark E W.Power System Stability，I and III[M]. New York：Wiley，1995.

[14]Portela C，Tavares C M. Modeling simulation and optimization of transmission lines-Applicability and limitations of some used procedures[C]//IEEE T&D Latin America.Sao Paulo，Brazil：2002.

[15]王冠，吕鑫昌，孙 秋 芹，等（Wang Guan，Lü Xinchang，Sun Qiuqin，et al）. 半波长交流输电技术的研究现状与展望 （Status quo and prospects of half-wavelength transmission technology）[J]. 电力系统自动化 （Automation of Electric Power Systems），2010，34（16）：13-18，68.

[16]黄 佳，王 钢，李 海 峰，等（Huang Jia，Wang Gang，Li Haifeng，et al）. 1 000 kV 长距离交流输电线路工频过电压仿真研究 （Study on simulation of fundamental frequency overvoltages for UHV AC transmission lines）[J].继电器（Relay），2007，35（4）：32-35，39.