冰灾情况下电网连锁故障的预防控制

阳江华，滕 欢，刘 明，朱椤方

（1.四川大学电气信息学院，成都610065；2.四川省智能电网重点实验室，成都610065；3.贵州电网公司电力调度控制中心，贵阳550002）

随着电力系统的结构越来越复杂，虽然供电可靠性逐渐增加，但在同时，由于各线路之间的相关性，某一条或几条线路断线就可能诱发整个电网发生大停电事故[1-2]。大停电事故多是由连锁故障引起，电力研究人员将连锁故障分为慢动态和快动态两个过程，快动态过程中的很多电力元件都会在很短的时间退出运行，不易控制，因此，最好在慢动态过程就能对之进行有效的预测并及时采取措施。

在我国南方地区，冬季的雨雪天气，极易使裸露在外的输电线路和输电设施形成大面积的覆冰，其覆冰厚度可能会超过导线设计的标准，导致线路断线故障，有的线路在未超过其设计标准时，覆冰造成的导线弧垂增大也可能使得导线之间或者导线与绝缘子之间的间隙变小，从而导致线路闪络发生[3]。2008 年1 月，在我国的南方各省，如浙江、江西、广西、湖南、云南、贵州等地的电力系统受到巨大影响，尤其是贵州、湖南两地最为严重，虽然发生灾害的原因也有一部分是绝缘子发生冰闪跳闸，但影响最为恶劣的是由于覆冰造成的线路过大载荷而断线，以及覆冰导线舞动引起的电力设备损坏。因此，若能及时预测出覆冰的厚度，并在线路因覆冰发生故障前进行融冰，或者在快要断线时提出预警或在初始故障发生后及时控制住故障传播，就能起到防控连锁故障的作用。

文献[4]针对四川的输电线路的覆冰特点，结合当今国内外用于防治冰灾的先进技术，提出了对覆冰事故的防御措施以及建议，它能在一定程度上反映目前冰冻灾害下电力系统存在的问题，但并未提出具体的解决方案。目前在连锁故障研究中考虑时间因素的研究已有很多；文献[5]是针对线路触树故障中引起大停电事故的崩溃序列以及对应的时间尺度问题；文献[6]是基于时序理论对系统的连锁故障过程进行路径搜索，并未涉及连锁事故的防治以及控制，也没有具体将其用于冰冻灾害中的电力系统；文献[7]采用电压/无功灵敏度法用于电压稳定分析，确定无功补偿的地点，并未涉及到有功方面的控制，也没用于故障的防控中。在冰雪天气下预防控制连锁故障的重要性是不言而喻的，但却鲜有文献提出一个具体的针对冰冻灾害的防控方法。

本文将曲线拟合、时间节点的选择和连锁故障的防控应用于冰灾情况下，研究了冰灾下的电网连锁故障防控方法。在覆冰严重的区域以及可能会导致线路发生连锁故障的区域进行覆冰厚度监控，基于最小二乘法建立覆冰厚度随时间增长的模型，根据线路设计冰厚，预测线路断线时刻，并通过合适的时间节点的选择，在覆冰厚度接近临界值时发出预警，在线路因覆冰达临界值而断线之前采取有效的调控措施，阻止第二次事故的发生，若不成功则继续调控，阻止下一次事件发生，直至连锁故障停止。仿真结果证明此方法的可行性。事实上，在实际的电力系统中，冰灾情况下线路断线与否并不仅仅与覆冰的厚度相关，还与导线档距、弧垂以及导线舞动有关，但这些因素所造成的后果主要是电力设备尤其是杆塔损坏。本文仅基于导线因载荷过大而断线的严重后果考虑，从导线覆冰厚度方面入手，及时预测断线时刻，并分两级预警以方便采取融冰或在线调控策略阻止事故扩大。

1 输电线路覆冰增长模型

1.1 覆冰厚度与时间模型建立

一般来说，在雨雪天气，导线表面的覆冰会逐渐加厚，随时间变化存在一定的规律，另外，现有的研究表明，其覆冰的厚度还与降雨量降雪量、海拔、温度、湿度、风速等因素有关。海拔一定的情况下，在较短的单位时间内，可以将温度、湿度等其他相关因素看作固定不变的，通过文习山等[8]的模拟实验以及拟合回归分析，得到导线覆冰质量与时间存在的指数关系为

式中：m 为覆冰质量；A 为关系系数；b 为时间影响特征指数。A 和b 在不同的环境条件下，取值不一样，无法直接确定，故只能通过观察厚度随时间变化的规律进而求出各未知的系数。

在相同的环境条件下，单位长度的导线上的覆冰质量与覆冰厚度存在的关系为

式中：ρ 为覆冰的密度；d 为导线外径，d 值为导线参数的一部分；δ 为覆冰厚度，δ 值可凭借观察测量得到。密度ρ 因不同的覆冰类型有不同的密度，根据相关研究[9]，雨凇密度大于或等于0.9 g/cm3，取值0.9；雾凇密度在0.05～0.50 g/cm3之间，取值0.30；混合凇的密度则为0.6～0.9 g/cm3之间，取值0.8。

1.2 参数求解

为了得到覆冰厚度与时间的关系，用于实际工况中预测故障发生的时间点，本文利用实时采集的覆冰厚度与质量的关系，采取最小二乘法拟合质量和时间的曲线，得到A 和b 的值，经过转换，即可得到厚度和时间的关系。拟合质量-时间曲线的步骤如下。

步骤1 收集按时间顺序排列的n 组输电线的覆冰厚度数据，依次记为z1，z2，…，zn以及对应的环境温度T1，T2，…，Tn，得到输电线覆冰厚度时间序列[z]，两个数据之间的时间间隔相等，为Δt。

步骤2 根据不同的温度对应的不同覆冰种类的密度计算出覆冰质量。

步骤3 将数据取某段时间内的测量值进行最小二乘法拟合，得到系数A 和b，拟合方法如下。

对式（1）两边取对数得

令M=ln m，A1=ln A，则有

使用时间t 及对应的计算得到的数据m 求取对应的M 值，用线性拟合方法求取系数，使得的值最小，即A1、b 的值满足条件

则计算A 值的公式为

则关于时间和厚度的关系式为

将观测线路的可承受厚度的临界值代入式（7），即可求解到线路覆冰厚度达到临界值导致断线的时刻。

2 时间节点选择

在防控过程中，涉及到几个时间节点的选取，这些时间节点之间必须满足一定的先后顺序和条件才能达到对连锁故障进行防控的作用，他们之间的先后关系如图1 所示。

图1 连锁故障防控时间序列Fig.1 Time series of prevention and control for cascading failures

图中，各个时间点表示的含义及其值的确定方法如下。

（1）t0是覆冰开始时刻。从这个时间点开始对线路的覆冰厚度进行监测并记录数据（每隔Δt 记录1 次数据）。

文献[10]中提到覆冰的基本过程是当气温在－5～0 ℃之间，风速较大（3～15 m/s）时形成雨凇；当气温在-16～-10 ℃之间，风速较小时形成雾凇；温度在－9～－3 ℃之间，即形成混合凇。又由于相对湿度维持在85%以上时，有利于积冰的增长和持续不融化。因此，在温度低于0 ℃、湿度大于85%且风速在3 m/s 以上时开始计时并记录覆冰厚度。

（2）Δt 是测量覆冰厚度时2 个相邻数据之间的间隔时间。其值不宜过大或过小，过小会使得数据更新速度太快，对曲线的拟合不利；而过大则会使拟合的曲线的精度不够。

在文献[9，11-12]的基础上，可以选择其值为1～12 h 之间。在覆冰刚开始且增长较慢的情况下12 h 记录1 次，在开始拟合曲线或增长较快时则1 h 记录1 次，或参照电网的实际情况选取。

（3）t1是拟合曲线的初始时刻。从这一时刻起，依次往后选取n 个时间点的数据进行曲线的拟合（为保证曲线拟合的准确性，n 的值应足够多，本文中n 取10）。覆冰初始阶段，厚度增长较慢，因此，t1值应该是在线路覆冰达到一定厚度时再开始对数据进行分析。

根据南方电网西电东送线路防冰警戒等级，当覆冰厚度达到线路极限厚度值的40%～70%时，属于中度覆冰，此时即需密切监测覆冰，所以从0.4 倍临界厚度的时刻作为t1的初始值。与此同时，不断更新数据来进行新一轮的曲线拟合，即改变t1，可以在其基础上叠加一个Δt，依次往后不断更新数据，以适应新的气候变化导致的覆冰变化情况。

（4）t2是根据拟合的曲线计算得到的故障发生时刻，即线路的覆冰厚度达到线路能承受的临界厚度时刻。以时间为横坐标，质量为纵坐标，利用第1 节中讲到的最小二乘法拟合得到质量随时间变化的曲线和关系式，并根据厚度和质量的关系计算出临界厚度对应的时间点即t2。

该时间点能大致反映该线路会在何时断线。确定好该时刻后，即可在断线之前采取一系列的预警、融冰及防控措施。

（5）t3是可以第1 次预警的时刻。此时的覆冰不应太厚，以方便融冰并且在断线前来得及采取融冰措施，由于计算到的断线时刻可能已经在不久以后，因此必须及时预警以便可以及时采取融冰措施。与预测到的断线时刻t2之间的时间间隔应该在留有一定的裕度情况下大于等于还来得及进行融冰的时间段。

通过调研，110 kV 及以上的直流融冰时间至少需8 h，加上向各级防冰工作小组申请融冰并调节电网运行方式以达到融冰条件所需时间，一般为10～24 h，所以，当预测到断线时刻t2在24 h 以内，就应采取第1 次预警（融冰条件较恶劣的部分地区可调整该值）。

但由于融冰所需时间较长，且在雨雪天气不一定能及时到达融冰地点，所以融冰措施不一定能及时采取，这就需要在适当的时候进行第2 次预警。

（6）t4是第2 次预警的时刻。若融冰措施由于种种原因不能采取，则需要进一步监控线路的覆冰厚度，在覆冰更多时第2 次预警，以采取针对该线路故障后可能发生的连锁事件的调控措施，应该满足其调控措施能在初始线路故障发生之前生效。根据文献[13]，在覆冰厚度达到导线设计值的80%时第2 次预警，此时应采取调节措施，使该线路断线后不至于造成事故的扩大，给调节措施采取留有的时间裕度为t2～t4。

（7）t5是在t2时刻线路断线之后，因调节措施失效而导致的第2 次连锁事件仍然发生的时刻。这个时间的确定，一方面是通过路径搜索时记录的故障时间，另一方面可以通过对继电保护元件的时间整定值计算得到。

在时间节点满足以上条件的情况下，几个时间点的控制也相互联系紧密，才能及时地进行预警、及时采取防控连锁故障的措施，才可能阻断连锁故障，防止事故扩大。

3 连锁故障控制

在电网恶劣运行方式下通过路径搜索的方式找到系统的薄弱环节，即一旦断线会引发其他线路故障造成严重后果的线路，对薄弱环节安装覆冰监控装置和预警设备。在系统预警之后，通过线路断线前的搜索结果，调节发电机出力和切负荷，使得初始故障线路断线后其负荷转移到其他线路上不至于导致断线，或者提前转移负荷来减小该线路上的负荷大小，从而减小该线路断线可能对系统造成的影响。本文采用一种基于电力系统静态有功灵敏度的分析方法计算支路有功灵敏度，对控制节点分级，生成控制策略来对预想的事故发生后的系统进行控制，确定有效的预防控制措施，并得到每一级事故的控制预案。

3.1 连锁故障路径搜索

选择一种运行方式，分别预设每一条线路为初始故障，模拟该故障引发的过负荷保护动作情况，根据断线情况判断该线路的故障是否会引起其他线路故障，通过路径搜索的方式对整个电网或者某个区域来事先获取连锁故障的序列，并得到的导致连锁故障发生的初始故障线路即为薄弱环节。这是因为电网规模巨大，不可能对每一条线路安装覆冰监控装置，第1、2 节提出的覆冰监控主要是针对预先搜索到的薄弱环节进行的。连锁故障序列搜索过程如图2 所示。

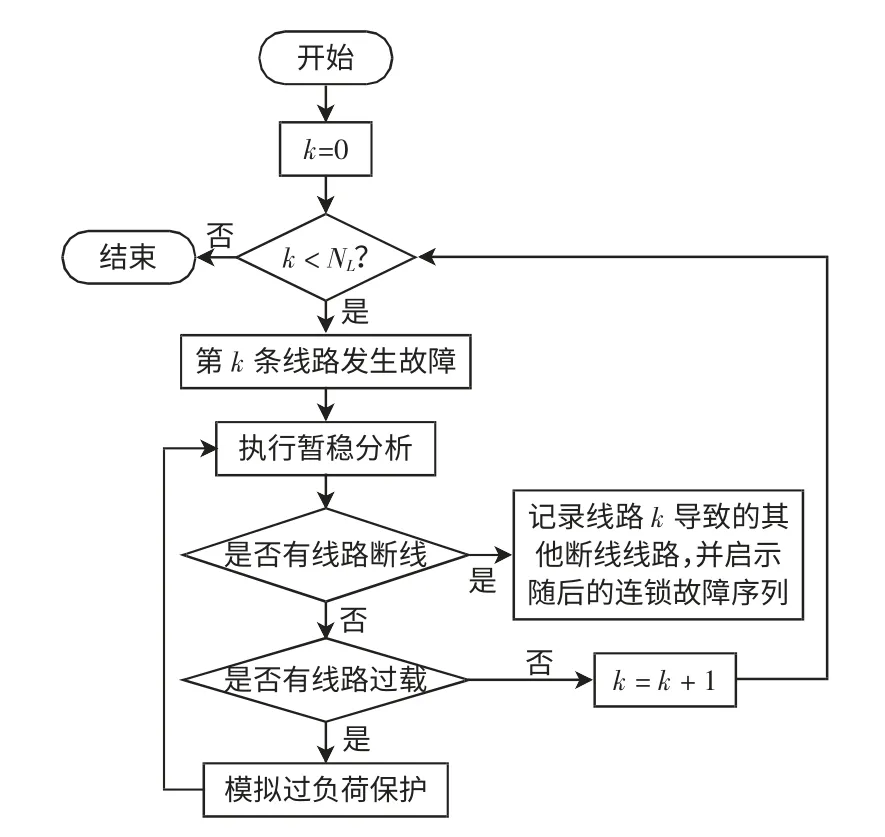
图2 连锁故障序列搜索过程Fig.2 Searching process of cascading failure’s path

在实际电网中，除了对路径搜索的薄弱环节进行监控之外，还应根据经验、历史数据等对覆冰严重区域中极易断线的线路进行重点监控。

3.2 静态灵敏度模型

连锁故障的二次事故往往是因过负荷保护动作而断线，通过考虑初始故障后的线路过载情况来制定措施，即调整影响该支路负载情况的发电机节点或者负荷节点的功率来降低过载程度。在电力系统的一个输电断面内，某一个节点的有功注入的改变，势必会影响其他支路的有功功率，将发电机和负荷节点q 改变一个单位的有功注入时，支路Li-j上的潮流变化值定义为该节点对该支路的静态有功灵敏度[14]，用SL-q表示，其计算公式为

式中：ΔPL为支路L 改变的有功功率；ΔPq为节点q改变的有功大小。

假定|gij|≪|bij|，θij很小，Ui≈Uj=1，采用直流潮流法计算节点q 和支路L 的有功功率，即

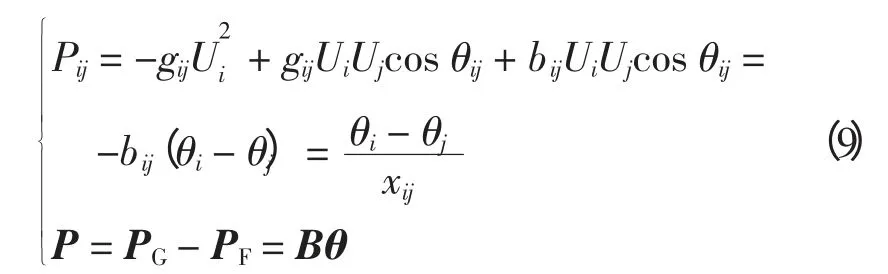
式中：P为除平衡节点以外的n-1 个节点的注入功率向量；PG、PF分别为节点出力和节点负荷；θ 为不包括平衡节点的n-1 个节点电压的相位向量；B 为节点导纳矩阵的虚部，与P-Q 解耦法有功迭代方程中的系数矩阵相同；Pij为支路Li-j的有功潮流；bij为支路导纳矩阵虚部；θij为节点i 电压相角同节点j 电压相角差；xij为支路电抗。

将式（9）变形，得

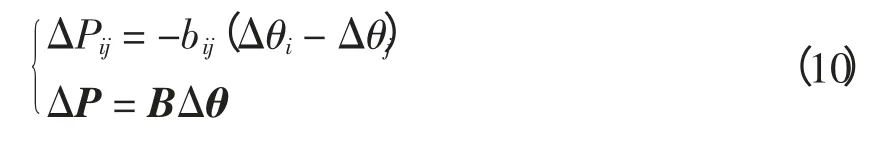
将ΔP=BΔθ 写为矩阵形式即

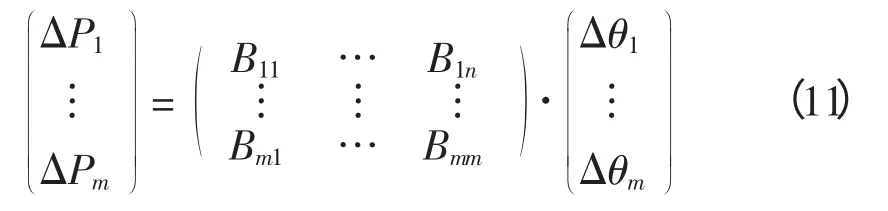
式中：m=n-1。

对节点q，当ΔPq=1 MW 时，代入式（11）可求得所有节点的Δθ，根据式（10）即求到任一支路的有功变化量ΔPij，即该节点对该支路的灵敏度。重复此步骤，求得由所有节点对应所有支路的灵敏度指标组成的灵敏度矩阵。

3.3 控制策略生成

控制策略，即对可能发生过负载断线的第2重事故线路进行减载调节控制。

首先对所有控制点进行分类分级。

（1）分类。排除不可控节点（如一些不可控发电机以及一些不能中断供电的一级负荷）后，根据灵敏度正负进行分类；

（2）分级。以机组为例，设置门槛值KG1、KG2，KG1〉KG2。将满足|SL-i|〉KG1（i=1，2，…）的节点i 划分为第1 级节点；将满足|SL-i|〉KG2（i=1，2，…）的节点i 划分为第2 级节点（包含第1 级节点）；第3极节点指所有可控点。设置负荷节点门槛值KF1、KF2，分级方法同发电机节点。

按照优先级顺序对系统调节，减小支路L 过载，若优先级高的节点调节量无法满足，再对优先级低的节点调节。

然后，求取初始控制量。在第1 级控制节点中，设发电机组成的集合为JG1，负荷组成的集合为JF1，设支路L 过载量为G，可调发电机组中灵敏度绝对值最小的节点的控制量为ΔPGmin，可调负荷中灵敏度最小的节点的控制量为ΔPFmin，令其满足条件|ΔPGmin|=|ΔPFmin|，求得各个节点的控制量为

最后，考虑约束条件，求最优控制量。调节过程中的约束条件有2 个：

（1）机组以及负荷的调节量导致其余正常线路的过载量不超过该支路的规定的最大过载量；

（2）各可调机组的控制量必须不超出机组所能提供的最大增发功率和最大减出力极限。

最优控制量即取满足上述2 个约束条件的最小控制量。

4 防控总流程

总结上述内容，防控总流程如图3 所示，通过该流程，可以起到预警冰灾、控制连锁故障的发生等作用。

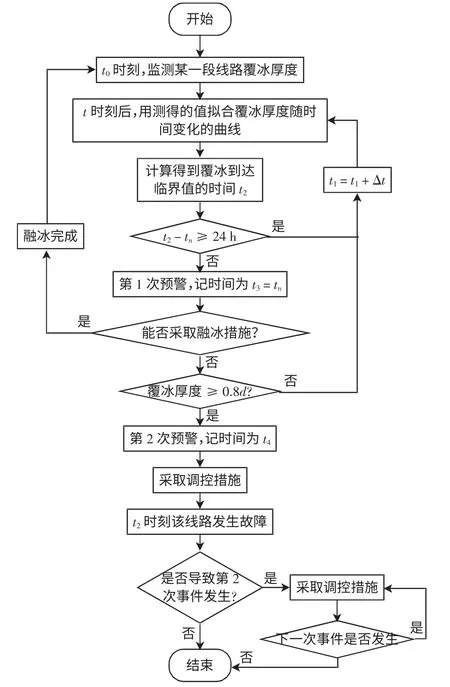
图3 防控总流程Fig.3 Total process of prevention and control

5 仿真算例

本节分两部分对文中所述方法进行仿真验证，第1 部分采用2011 年1 月初我国南方某地区一回110 kV 线路采集的实际冰厚数据，计算单位长度覆冰质量，用Matlab 编程计算系数A、b，求得覆冰厚度和时间的关系式，由线路覆冰厚度设计值来预测线路断线时刻，与实际断线情况作对比验证该模型的正确性；第2 部分则对IEEE30 节点的标准系统进行防控仿真分析，采用Matlab 编程的方法搜索出连锁故障序列，选择薄弱线路为初始故障，进行防控分析，计算出调发电机及调负荷的量，在BPA 软件中调节发电量和负荷量对之进行各级调节，验证经过采取控制措施后该线路不会发生连锁故障。

5.1 覆冰模型仿真

自2010-01-01 起，该地区的气温就在0 ℃以下，每日天气也以冻雨和雨夹雪居多，微风，达到了覆冰条件，覆冰类型为雨凇，密度取0.9 g/cm3。该110 kV 线路采用导线型号为LGJ-240/55，计算外径为22.4 mm，其覆冰厚度设计值为20 mm。

记2010-01-01 12：00 为覆冰开始时间t0，由于一开始覆冰增长很缓慢，电力公司每12 h 观察一次厚度，到2010-01-05 8：00 起厚度已达8 mm，记此时刻为t1，此后的数据将用于拟合曲线。为方便计算保证拟合准确性，相邻的数据的时间间隔取3 h，且记t1=0，2001-05—2001-07 具体的数据如表1 所示。

第1 次仿真：取前10 个数据，按照最小二乘法得A=686.37，b=0.015 3，计算得到厚度为20 mm 时t=81.7，即在54.7 h 即大于24 h 以后，故继续进行第2 次仿真；

第2 次仿真：取第2 至11 个数据，得A =684.54，b=0.015 4，厚度达20 mm 时t = 81.3，在51.3 h 即大于24 h 后，故进行第3 次仿真。

以此类推，直到第11 次仿真，计算得A =677.17，b=0.015 8，厚度20 mm 时t≈80，即在23 h，小于24 h，取该次仿真结果，如图4 所示。

因此，此时（2010-01-07 17：00）应采取第1 次预警，然后根据实际情况判断是否采取融冰操作。

根据预测，会在2010-01-08 16：00 左右断线，据该电网实际的统计数据显示2010-01-08 19：25，该线路覆冰厚度超过其极限值20 mm，线路断线，比预期时间晚3 个多小时，说明本文提出的该覆冰厚度模型基本正确。若不能进行融冰，根据第11次仿真结果计算覆冰厚度为18 mm 时t=70.3，即第2 次预警的时间为2010-01-08 7：20 左右，在第2 次预警后留有的时间裕度为10 h 左右，已足够采取防控措施。

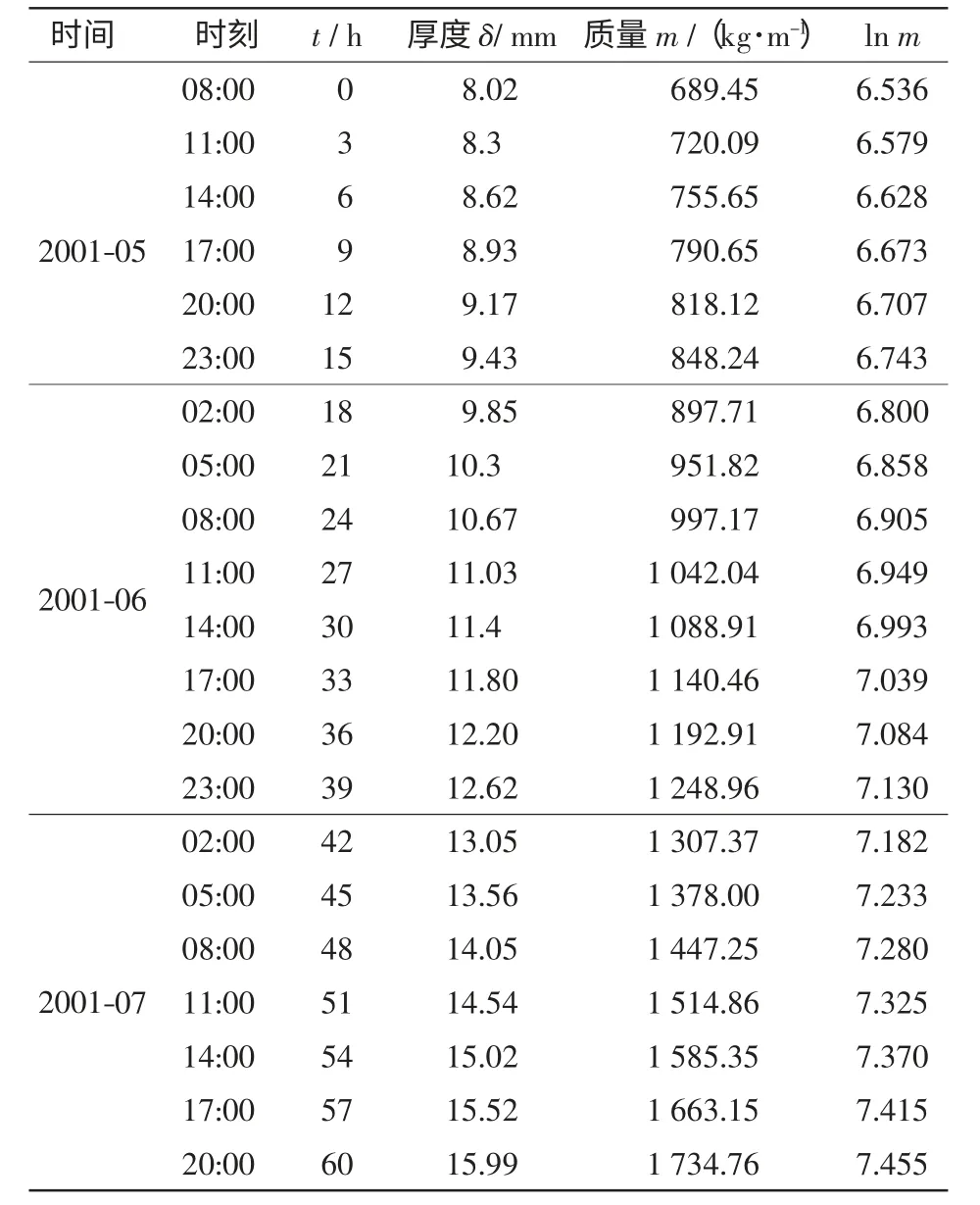
表1 2001-05—2001-07 覆冰情况Tab.1 Icing condition in January 5th-7th

图4 覆冰质量-时间曲线Fig.4 “m-t”curve of the icing

5.2 防控策略仿真

IEEE30 节点标准系统结构如图5 所示，该系统包括6 台发电机，41 条支路，负荷节点18 个，由于连锁性事故不考虑变压器支路故障，该仿真只考虑删去变压器支路的剩余37 条支路。

对该系统进行路径搜索，得到的连锁故障路径如表2 所示。

表2 中，当L4发生断线故障时，若不采取控制措施，将会发生下一级故障（L6断线），因此为防止连锁故障下一级故障的发生，对发电机或者负荷进行调整。首先对发电机进行调整，若无法抑制下一级故障的发生，再对负荷量进行调整，并重新调整发电机的出力。本节在仿真中认为所有的发电机组均为可调节机组，将6 台发电机进行出力调整，调整的机组有功值和无功值如表3 所示。

图5 IEEE30 节点系统Fig.5 IEEE30 bus system

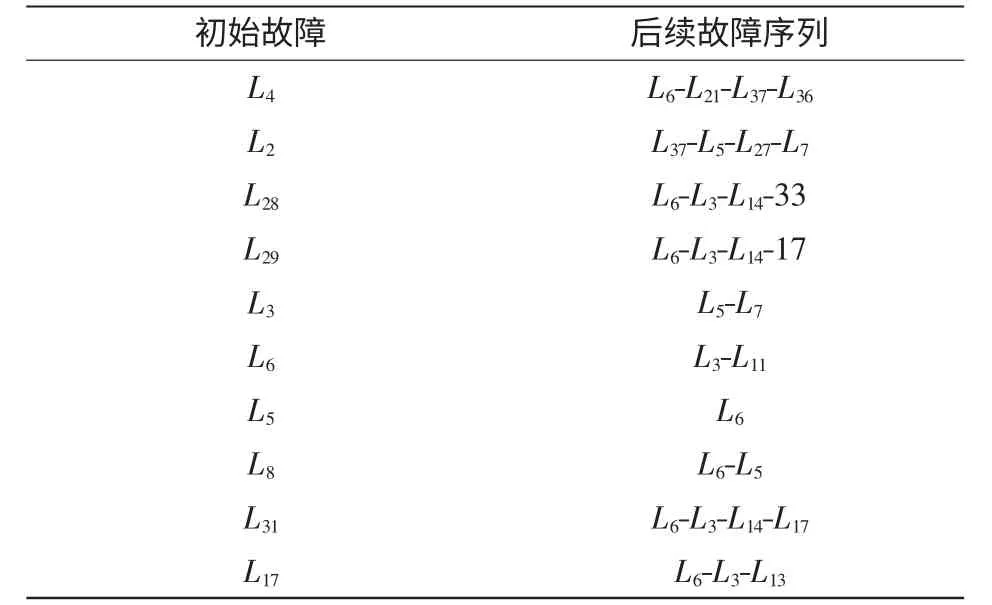
表2 连锁故障路径搜索结果Tab.2 Searching result of cascading failure path

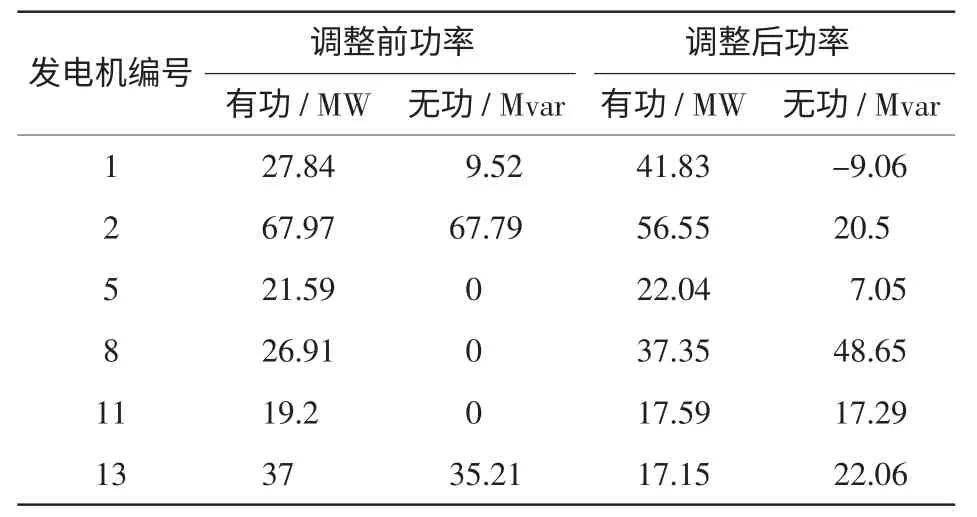
表3 L4 断线前调节措施Tab.3 Adjustment measures before L4 breaking

实验表明，调节后L6不再断线，第2 级故障得到了控制。

若调控第1 级控制时间来不及，则迅速调用第2 级控制措施，即对L4和L6断线之后的情况预先进行调节，使事故不至于扩大。调整的有功、无功如表4 所示。

表4 L4、L6 断线前调节措施Tab.4 Adjustment measures before L4&L6 breaking

仿真表明，调整后L4、L6断线不会导致下一级事故发生，即第3 级故障得到了控制，该仿真证明了该防控方法的正确性。

7 结语

本文所提出的根据实时厚度数据基于最小二乘法的覆冰模型，用于拟合出覆冰质量随时间变化的关系。利用该曲线可预测线路达冰厚临界值的时间，综合各项因素选择的时间节点给线路因覆冰发生故障前的融冰留出充分的时间裕度，并在不能融冰的情况下对初始故障发生前及时控制第2 级故障的继续传播，并留出时间裕度，若不成功则继续调控，阻止下一次事件发生，直至连锁故障停止。仿真说明曲线拟合的方式可起到预测线路断线的作用，防控措施也能起到防控连锁故障的作用。但由于目前对冰灾的监控力度不够，在实际运行情况下仅对少量线路安装有覆冰厚度监测装置，且很难将所有的冰厚数据保存下来，因此本文的方法用于实际电网还有一定的限制，对电网冰灾下连锁故障的防控也还需要在实际系统中进行进一步的综合考虑研究。

[1]邹 江 峰，章 显 亮（Zou Jiangfeng，Zhang Xianlang）. 巴 西“2009.11.10“和”2011.2.4”大停电事故及启示（Summary and revelation of “2009.11.10”and “2011.2.4” blackouts in Brazil power system）[J]. 中国电力（Electric Power），2011，44（11）：19-22.

[2]张国华，张建华，杨志栋，等（Zhang Guohua，Zhang Jianhua，Yang Zhidong，et al）. 电力系统N-K 故障的风险评估方法（Risk assessment methodb of power system N-K contingencies）[J]. 电网技术（Power System Technology），2009，33（5）：17-21，27.

[3]吴昕婷（Wu Xinting）. 基于电力系统的自然灾害应急管理研究（Research on natural disaster emergency administration of electric power system）[J]. 武 汉 理 工 大 学 学 报社：会科学版（Journal of Wuhan University of Technology：Social Science Edition），2008，21（2）：188-191.

[4]陈 向 宜， 何 朴， 刘 明 忠 （Chen Xiangyi，He Pu，Liu Mingzhong）. 四川电网输电线路覆冰分析及防御措施（Analysis of the ice-coating and the protective measure in Sichuan power grid）[J]. 四川电力技术（Sichuan Electric Power Technology），2011，34（2）：41-43.

[5]张龙跃，肖先勇，马超（Zhang Longyue，Xiao Xianyong，Ma Chao）. 基于线路触树故障时间的连锁故障防治研究（Prevention of cascading failures based on time of vegetation-related failure）[J]. 华东电力（East China Electric Power），2012，40（8）：1350-1355.

[6]郝达智 （Hao Dazhi）. 基于时序理论的连锁故障模式搜索方法研究（Pattern Search Method Research of Cascading Outage Based on Time Sequence Theory）[D]. 北京：华北电力大学电气与电子工程学院（Beijing：School of Electrical and Electronic Engineering， North China Electric Power University），2009.

[7]刘君华， 方鸽飞， 吕岩岩 （Liu Junhua，Fang Gefei，Lü Yanyan）. 基于灵敏度法确定无功补偿地点（Allocation of reactive compensation using sensitivity analysis approach）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（4）：58-61.

[8]文习山，龚宇清，姚刚，等（Wen Xishan，Gong Yuqing，Yao Gang，et al）. 导线覆冰增长规律的试验研究（Experimental study on growth law of conductor’s icing）[J].高电压技术 （High Voltage Engineering），2009，35（7）：1724-1729.

[9]虢韬，刘锐（Guo Tao，Liu Rui）. 贵州省高压输电线路覆冰情况与观冰方法研究（Discuss on icing condition and method of observation ice on Guizhou high voltage transmission lines）[J]. 水电能源科学（Water Resource and Power），2011，29（11）：167-170.

[10]朱君，向卫国，赵夏菁（Zhu Jun，Xiang Weiguo，Zhao Xiajing）. 贵州导线覆冰的致灾机理研究（Study on disaster-causing mechanism of wire icing in Guizhou）[J]. 高原山地气象研究 （Plateau and Mountain Meteorology Research），2011，31（4）：42-50.

[11]张志劲，黄海舟，蒋兴良，等（Zhang Zhijin，Huang Haizhou，Jiang Xingliang，et al）. 交流输电导线覆冰增长及临界防冰电流的试验研究（Experimental research on the icing accretion and its critical anti-icing current for conductors under AC condition）[J]. 高电压技术（High Voltage Engineering），2012，38（2）：469-475.

[12]刘春城，刘佼（Liu Chuncheng，Liu Jiao）. 输电线路导线覆冰机理及雨凇覆冰模型（Ice accretion mechanism and glaze loads model on wires of power transmission lines）[J].高电压技术 （High Voltage Engineering），2011，37（1）：241-248.

[13]曹敏， 罗学礼， 石少勇， 等 （Cao Min，Luo Xueli，Shi Shaoyong，et al）. 基于覆冰增长速度的覆冰在线监测系统动态预警方案研究与探讨（Research and discussion on dynamic warning program of on-line icing monitoring system based on the growth rate of icing）[J]. 南 方 电 网 技术（Southern Power System Technology），2009，3（S）：187-189.

[14]赵迪 （Zhao Di）. 基于灵敏度分析方法的电网越限调整措施研究（Research on the Adjustment Measures of Power Grid Violation Based on Sensitivity Analysis Method）[D].保定：华北电力大学电气与电子工程学院（Baoding：School of Electrical and Electronic Engineering，North China Electric Power University），2010.