适用于波长交换光网络的波长旋转图模型设计
2010-08-14赵继军张曙光赵文玉
赵继军,张曙光,赵文玉
(1. 河北工程大学 信息与电气工程学院,河北 邯郸 056038;2. 工业和信息化部 电信传输研究所,北京 100045)
1 引言
在解决波长交换光网络(WSON)的路由与波长分配(RWA)问题时,无论是把RWA问题拆分为路由和波长分配2个子问题,还是利用启发式算法解决RWA问题都需要考虑波长分配问题[1~4],目前在解决波长分配子问题时一般是基于分层图的思想,分层图对于解决具有波长一致性限制的RWA问题十分有效[5,6],但解决具有波长智能调度的RWA问题时,就显得不是十分有效[7~9],主要存在波长转换的次数选择、波长转换节点确定、波长分配繁琐等多种限制。本文根据波长智能调度的需要提出了一种基于波长转换旋转图模型解决RWA问题的思想,并构建了波长转换旋转图模型和提出基于新模型的路由波长分配新策略。仿真结果表明,基于波长旋转模型的波长分配策略可以有效降低网络的阻塞率,提高全网资源利用率。
2 波长旋转图模型设计
2.1 波长分层图模型分析
利用分层图模型解决具有波长一致性限制的RWA问题是有效的,因此,近年来很多文献利用分层图模型解决RWA问题,文献[6]提出了一种基于分层图的最大边不相关RWA算法;文献[7]利用分层图方法来记录WDM网络状态,提出了一种链路状态描述模型;文献[8]基于分层图模型提出了一种解决 WDM 网络的动态路由和波长分配问题的算法;文献[9]基于分层图提出了一种在WDM网状网中支持多种可靠要求的业务量疏导算法,但是文献[6~9]利用分层图模型解决的都是具有波长一致性约束限制的RWA问题,如果利用现有的分层图模型解决具有波长转换能力的WDM网络RWA问题,就需要考虑层与层之间的倒换,具体分析如下。
波长路由光网络的物理拓扑以无向图G(V,E,W)表示,其中, V、E、W 分别表示网络的节点集合、双向链路集合(每个链路由 2根方向相反的单向光纤构成)和每个链路的波长集合(每根光纤所支持的波长数相同)。波长分层图模型的物理拓扑是利用分层图 LG(V*,E*)来描述,分层图 LG(V*,E*)是把网络拓扑中的物理拓扑复制成相同的|W|份,每一份为一层,对应波长集W中的一个波长iλ(其中i=1,2,…,|W|)。
假设W=3,图1所示的物理拓扑图就变成分层图(如图2所示),在波长分层图模型中形成了3层,自上而下对应的波长依次为1λ、2λ和3λ。当模型中源—目的节点对之间满足波长连续性限制时,形成的光通路在同一个波长分层内。对于一个连接请求,应用分层图模型实现了路由和波长分配的并行计算,它所经过的光路径,就是该光连接在物理拓扑上经过的路径,光连接所在的波长分层就是光连接所占用的波长。图 1中的光连接请求(V1,V4)在图 2中建立的光路径是,即该光连接请求在物理拓扑中的路径为V1→V2→V3→V4,且该光连接请求被分配的波长为λ1。因此,基于分层图模型的RWA算法非常适用于解决具有波长连续性限制的RWA问题。但是,若源—目的节点对之间的节点具有波长转换能力,形成的光通路就有可能在不同波长分层中,具体到分层图模型中,一个光连接请求进行路由和波长分配时,就不仅仅是在一个波长分层中进行计算,图1中的光连接请求( V1,V4)在图2中建立的光路径可能有等,该光连接请求在物理拓扑中的路径仍然为V1→V2→V3→V4,但是在具备波长转换能力的网络环境下,该光路径的每个链路上分配的波长就不一定完全都是λ1,某条链路上分配的波长可能是λ2或λ3,不再受波长一致性的限制。

图1 波长路由光网络的物理拓扑
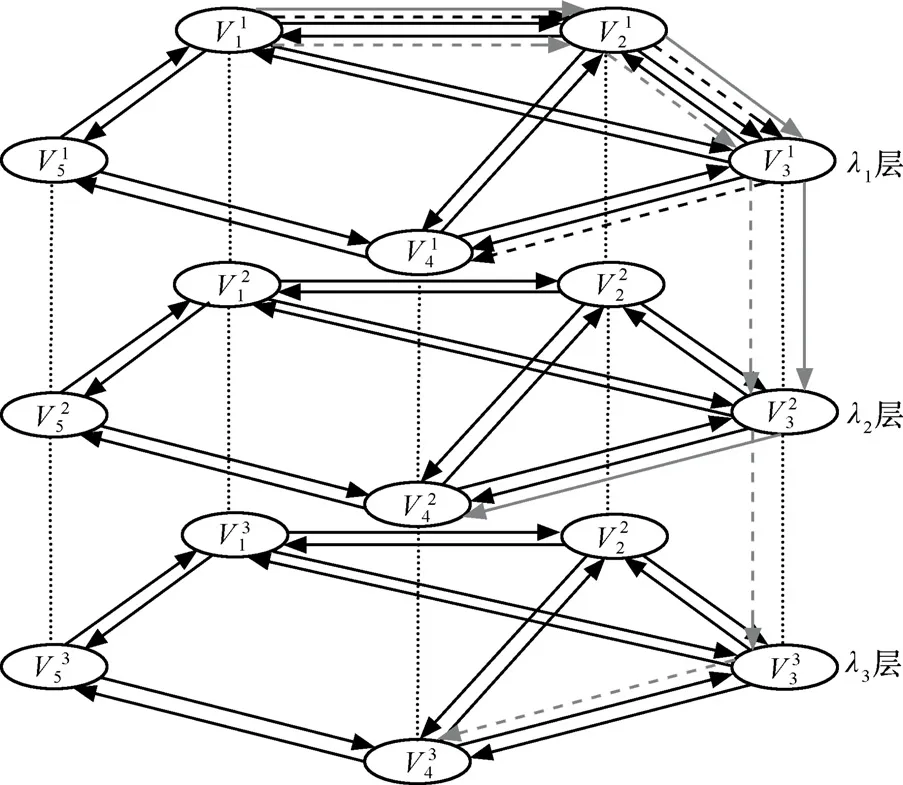
图2 波长路由光网络波长分层图模型
通过对分层图模型的分析发现,任意的一个光连接请求从源节点到达目的节点在同一波长分层内选择路由,并且每条链路只允许一个光连接经过,较好地满足了波长一致性约束限制下的RWA问题的解决。然而,基于分层图解决具有波长转换能力的 RWA问题时,主要是在选择光通路时选择一条或几条代价为0的虚链路,但是如果这样就增加了选路的时间,同时还存在如下 3个问题:1)在哪个节点处进行波长转换?2)用何种波长转换策略?3)如何分配波长?因此,本文就想如何不用选择一条或几条代价为0的虚链路也能解决具有波长转换能力的 RWA问题,所以在本论文中提出了一种波长旋转图模型(WRG,wavelength rotation graph),并构建了波长旋转图模型,在该模型上不仅可以同时解决WDM网络中的选路和波长分配问题,还使波长在节点处智能调度可行。
2.2 波长旋转图模型定义
波长旋转图模型的物理拓扑利用旋转图RG (V*, E*)来描述,旋转图模型是将物理拓扑中节点Vi到节点Vj的物理链路eij依据平均分配的原则分成W个波长链路,每一个虚链路可以逻辑依附在旋转椭球体的表面,分别为,, … ,,如图3所示,形成波长旋转图中的W条链路,即物理拓扑中节点Vi到节点Vj的链路eij对应并且原来的双向链路变成方向相反的 2条有向链路,Vi,Vj∈ V ,eij∈ E 。这样,旋转图 R G(V*, E*)的每一链路都代表一个波长,按顺序对每一链路所对应的波长进行编号,依次为 λ1, λ2, … ,λW。

图3 波长旋转图模型链路分解
假设W=3,波长旋转图的每一链路所对应的波长依次为λ1,2λ和3λ,则图1中所示的物理拓扑利用旋转图就转变为图4所示。
分析可知,在波长分层图模型中,光路从源节点到目的节点必须受波长一致性约束限制。对于波长旋转图模型,一个连接请求,可在波长旋转图上进行选路,它所经过的路径,就是该光连接在物理拓扑上经过的路径,光连接的各个链路对应的波长就是虚链路所对应的波长,较好地适应了波长转换条件下的选路要求。
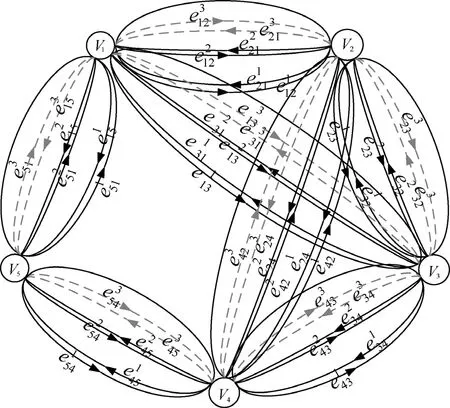
图4 波长旋转图模型网络链路分解
2.3 基于波长旋转角的波长分配策略
基于波长旋转图模型利用RWA算法进行选路和波长分配,通过OSPF算法能够直观地找到光连接在物理拓扑上经过的链路,但光连接所经过的链路上波长分配就需要根据网络波长资源求解,首先需要解决波长分配问题,为了有效解决这一问题,在波长旋转图模型的基础上提出了波长旋转角的概念。
波长旋转图的旋转角定义为:把节点Vi到节点Vj的链路eij分解成虚链路,,…,,并且都依次依附在旋转球体的表面,任意虚链路之间夹角称为波长旋转图的旋转角,记为。
定义波长旋转图的旋转角是想通过旋转角能够在选路的同时直接分配波长,也就是利用虚链路和之间的旋转角 α imjn进行波长分配,节点Vi到节点Vj之间选择波长思路如下。
1) 置K=1,若节点Vi的上一节点与节点Vi之间分配的波长是sλ,判断节点Vi与节点Vj之间的波长sλ是否空闲,若空闲,则给链路分配波长sλ,并把该链路的波长sλ置为已占用;否则,转到步骤 2)。
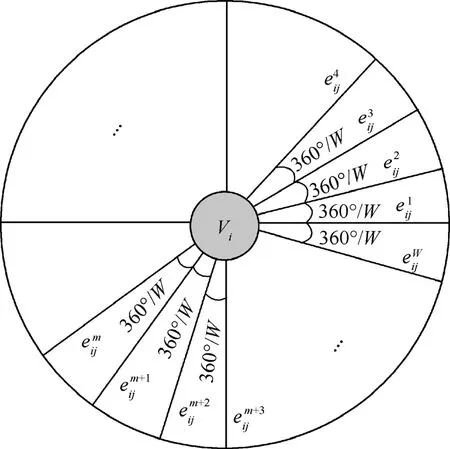
图5 波长旋转图节点对之间虚链路投影
2) 节点Vi和节点Vj之间的旋转图以ViVj为轴逆时针旋转 360。/W 度,判断波长λs+K是否空闲,若空闲,则分配波长;若已占用,则K+1,然后重复步骤2)直至K=W。其中:s代表被分配波长的波长数;sλ代表节点Vi的上一节点与节点Vi之间分配的波长是第s个波长资源;K是一个控制变量,它的作用就是在节点Vi与节点Vj之间选择波长时,使节点Vi与节点Vj之间没有空闲的波长资源,从而不会出现死循环;λs+K代表分配的波长资源是第s+K个波长。
综上所述,通过波长旋转图模型的构建,提供了一种基于波长旋转角的波长分配策略,可以同时解决具有波长转换能力的选路和波长分配问题,因此本文构建的波长旋转图模型在 WSON网络中具有较好的适用性。
3 基于波长旋转图模型求解RWA问题的过程
由于RWA问题是一个NP完全问题[3,8],一般将其分成路由和波长分配2个子问题分别解决。本文提出的波长选转图模型将RWA问题转化为在波长旋转图上给最短路径分配波长,并没有改变 RWA问题是一个NP完全问题的特性,所以基于波长旋转图的RWA问题仍然是NP问题。因此,基于波长旋转图模型的RWA算法仍然通过将RWA问题拆分为路由和波长分配2个子问题的思想。
构建波长旋转图模型的目的是为了能够更好地解决WSON中的RWA问题,在本节将对基于波长旋转图模型求解 RWA问题的思路进行详细分析。下面通过图4中的波长旋转图来具体阐述基于波长旋转图的RWA问题求解过程,当业务连接请求(V1,V4)到达网络时,假设网络中与业务请求(V1,V4)有关的链路的状态如表1所示。
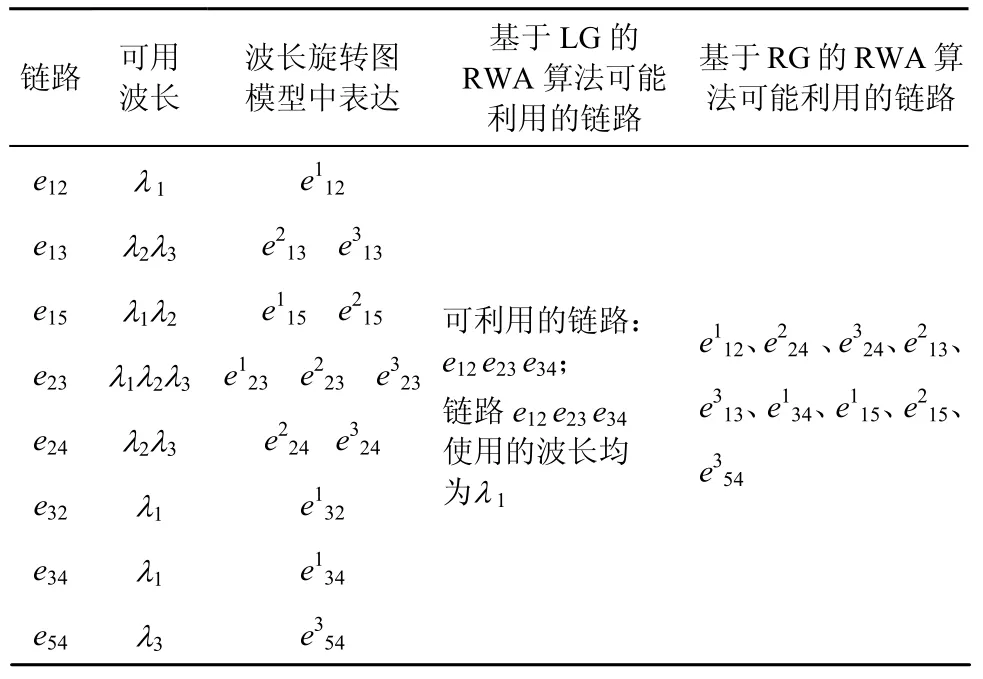
表1 网络中与业务请求(V1,V4)有关的链路状态
根据表 1,业务请求(V1,V4)可选择路径有V1→ V2→ V4、 V1→ V3→ V4、 V1→ V5→ V4、V1→V2→V3→V4、V1→V3→V2→V4;在这 5条 路 径 中 , V1→ V2→ V4、 V1→ V3→ V4、V1→ V5→ V4、V1→V3→V2→V44条路径均无连续可用波长资源,路径 V1→V2→V3→V4有连续可用波长。若RWA算法基于分层图模型实现,则只能选择路径 V1→V2→V3→V4;若RWA算法基于波长旋转图模型,由于考虑了波长转换能力,按照跳数最少的原则可以选择 V1→ V2→ V4、V1→ V3→ V4、 V1→ V5→ V4,从上面例子可以定性地得知利用波长旋转图模型不但可以解决波长智能调度问题,还可以改善波长资源利用率。
通过前面论述和分析可知,利用波长旋转图模型解决RWA问题是有效可行的,下面给出基于波长旋转图模型求解RWA问题的流程,如图6所示。
流程中的T是一个控制变量,它的作用是在选择源-目的节点对之间光路径时,使WRG-RWA算法不会陷入死循环,Const是一个常量,其值通常为业务请求的最大跳数(不同网络拓扑的 Const值不同);s和K的含义与上一节中的s和K含义相同。

图6 基于波长旋转图的RWA(WRG-RWA)算法流程
通过上面的介绍,基于波长分层图的RWA算法可以实现波长可变的路由,但是在选择光通路时还需要选择一条代价为0的虚链路,若波长转换次数相对较多,则选择代价为0的虚链路数也就相对较多,这样就增加了选路的时间。而基于波长旋转图的 RWA算法在选择光通路时则不需要选择一条代价为0的虚链路,这样就节省了选择一条代价为0的虚链路的时间,因此,基于波长旋转图的 RWA算法就在一定的程度上节省了选路时间。从时间复杂度分析,基于波长分层图的RWA算法和基于波长旋转图的 RWA算法的路由算法都采用 OSPF算法,时间复杂度相同,主要区别在波长分配上,基于波长分层图的RWA算法在波长分配时最坏情况下时间复杂度为O(H|W|),基于波长旋转图的RWA算法在波长分配时最坏情况下时间复杂度为 O(|W|H)(其中,H是光路径的跳数,|W|是光纤链路上的波长数)。举例说明,当跳数为3,波长数为8时,38=6 561>83=512,即在最坏情况下,WLG- RWA算法在波长分配时的时间复杂度远大于 WRG-RWA算法在波长分配时的时间复杂度。
4 仿真结果与分析
基于前述思路,本文对基于波长分层图的RWA(WLG-RWA)算法和基于波长旋转图的RWA(WRG-RWA)算法进行了对比仿真研究。WLG-RWA算法中路由算法采用OSPF算法,波长分配使用首次命中(FF)算法;WRG-RWA算法的仿真过程中仍然采用OSPF算法进行路径计算,从计算出的路径中利用旋转图的思想进行波长分配。采用美国NSFNET网络作为仿真网络拓扑(如图7所示),包含14个节点,21条链接的网络,每条链接代表了一对双向光纤。在NSFNET中,本文假设最大波长数分别为4和8,并且每个光节点的信息处理速率相同,业务连接请求是动态业务,服从平均分布,并且网络具有完全波长转换能力。通过仿真,主要进行网络的阻塞率、全网波长资源利用率和算法运行时间3个指标参数的分析。

图7 仿真中使用的NSFNET网络拓扑结构
当每根光纤中最大传输波长数为 4时,使用WLG-RWA算法和WRG-RWA算法对比的仿真结果如图8所示;当每根光纤中最大传输波长数为8时,使用WLG-RWA算法和WRG-RWA算法对比的仿真结果如图9所示。仿真结果表明,每条链路的总波长数为4或8,WRG-RWA算法的阻塞率都有效降低。当每条链路的总波长数为 4时,使用WRG-RWA算法比使用WLG-RWA算法的阻塞率平均降低5.03%,当每条链路的总波长数为8时,使用WRG-RWA算法比使用WLG-RWA算法的阻塞率平均降低9.71%,可以看出在波长数较多时,连接请求阻塞率性能提升较为显著,这是因为随着波长数的增加,在利用旋转图进行波长分配时可以利用的波长增加了,使业务连接请求被阻塞的概率大大降低,这样,很自然地使连接请求阻塞率性能提升较为显著。
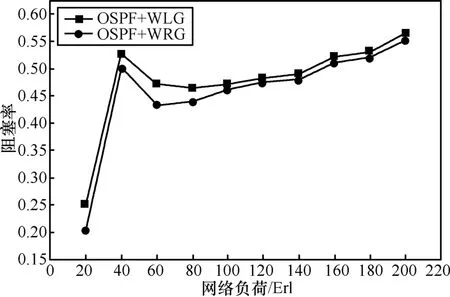
图8 阻塞率对比(4个波长)
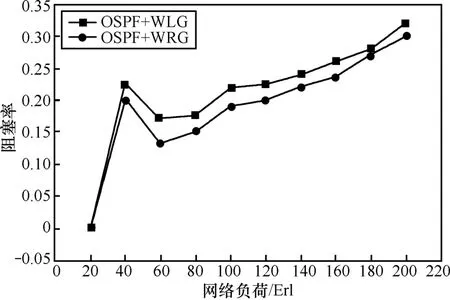
图9 阻塞率对比(8个波长)
图 10和图 11给出了 WLG-RWA算法和WRG-RWA算法的资源利用率对比图,分别使用4、8作为每条链路的总波长数。仿真结果表明,每条链路的总波长数为4或8,WRG-RWA算法的资源利用率均有显著提高。当每条链路的总波长数为4时,使用WRG-RWA算法的阻塞率比使用WLG-RWA算法的资源利用率平均提高 3.3%,当每条链路的总波长数为8时,使用WRG-RWA算法的比使用WLG-RWA算法的资源利用率平均提高1.54%。从图10和图11可以看出在波长数较多时,全网的资源利用率明显下降,这是因为总波长数增加,使利用旋转图选择波长时被分配的波长的使用频率降低,这样,很自然地使全网的资源利用率明显下降。
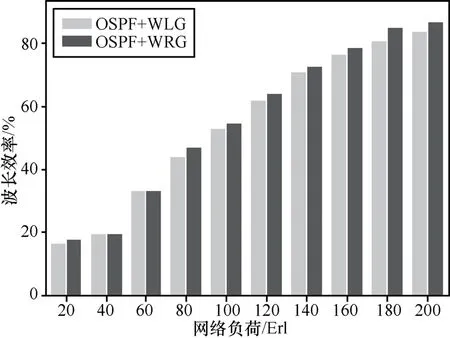
图10 资源利用率对比(4个波长)
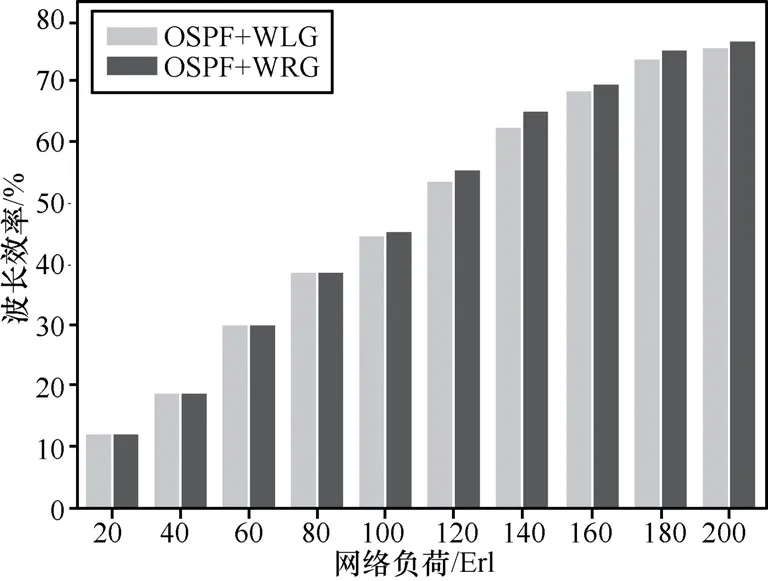
图11 资源利用率对比(8个波长)
图 12和图 13给出了 WLG-RWA算法和WRG-RWA算法的运行时间对比,分别使用 4、8作为每条链路的总波长数。从图中可以看出,每条链路的总波长数为4或8时,WRG-RWA算法的运行时间均明显降低,这恰恰说明了在最坏情况下,WLG-RWA算法在波长分配时的时间复杂度远大于WRG-RWA算法在波长分配时的时间复杂度。

图12 算法运行时间对比(4个波长)
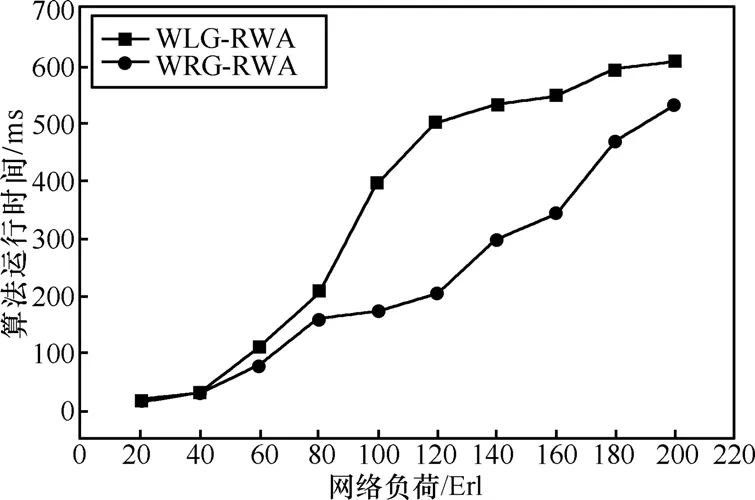
图13 算法运行时间对比(8个波长)
通过对网络的阻塞率、全网波长资源利用率 2个指标参数的对比分析,WRG-RWA算法的阻塞率明显降低,全网资源利用率明显提高。所以,通过仿真和分析可以得出结论,旋转图模型可以解决具有波长转换限制的RWA问题,而且WRG-RWA算法比 WLG-RWA算法更适合解决具有波长转换限制的RWA问题。
5 结束语
本文提出了一种基于波长旋转图模型解决具有波长转换能力RWA问题的方法,并通过将网络虚拓扑链路及关联波长均匀分布到旋转球体的表面,构造了一种新型的波长旋转图模型,而且提出了相应的波长分配策略和 RWA算法。通过仿真验证和分析,旋转图模型可以有效解决具有波长转换限制的RWA问题,而且WRG-RWA算法比WLG-RWA算法更适合解决具有波长转换限制的RWA问题。
[1] 杨春勇, 王文珍, 刘德明等. 一种全光波长路由器的设计及性能分析研究[J]. 电子与信息学报, 2008, 30(2):455-458.YANG C Y, WANG W Z, LIU D M, et al. Design and performance analysis of an all-optics wavelength router[J]. Journal of Electronics &Information Technology, 2008, 30(2): 455-458.
[2] AZODOLMOLKY S, KLINKOWSKI M, MARIN E, et al. A survey on physical layer impairments aware routing and wavelength assignment algorithms in optical networks[J]. Computer Networks,2009,53(7):926-944.
[3] MAEKOVIC G Z, TEODOROVIC D B, ACIMOVIC-RASPOPOVIC V S. Routing and wavelength assignment in all-optical networks based on the bee colony optimization[J]. AI Communications, 2007, 20(4):273-285.
[4] POINTURIER Y, BRANDT-PEARCE M, SUBRAMANIAM S, et al.Cross-layer adaptive routing and wavelength assignment in all-optical networks[J]. IEEE Journal on Selected Areas in Communications,2008, 26(6):1-13.
[5] BERTHOLD J, SALEH A A M, BLAIR L, et al. Optical networking:past, present and future[J]. Journal of Lightwave Technology,2009,29(9):1104-1117.
[6] 王汝言, 张普钊, 隆克平等. WDM 网络中一种基于分层图模型的RWA算法[J]. 光通信技术, 2007, 31(10):4-6.WANG R Y, ZHANG P Z, LONG K P, et al. A layered graph-based RWA algorithm in WDM networks[J]. Optical Communication Technolgy, 2007, 31(10):4-6.
[7] 葛晨晖, 黄晋竹, 孙小菡等. 自相似业务下共享通道保护WDM网络性能分析[J]. 电子与信息学报, 2006,28(11):2148-2151.GE C H, HUANG J Z, SUN X H, et al. Performance of WDM network with shared-path protection under self-similar traffic[J]. Journal of Electronics & Information Technology, 2006,28 (11):2148-2151.
[8] 肖诗源, 刘贤德, 金鑫. 一种波长转换受限WDM网络的动态路由和波长分配算法[J]. 电子学报, 2005,33(6):1140-1142.XIAO S Y, LIU X D, JIN X. An algorithm for dynamic routing and wavelength assignment in WDM network with limited wavelength conversion[J]. Acta Electronica Sinica, 2005,33 (6):1140-1142.
[9] 赵继军,雷蕾,纪越峰等. 一种基于ASON的新型动态恢复路径建链协议[J]. 通信学报, 2003, 24(5):85-93.ZHAO J J, LEI L, JI Y F, et al. A novel ASON-based dynamic restoration path setup protocol[J]. Journal on Communications, 2003, 24(5):85-93.
