炮口速度对弹丸飞行稳定性的影响
2015-03-04刘志林王雨时张志彪刘锦春颜秀红
刘志林,王雨时,闻 泉,张志彪,刘锦春,颜秀红
(1 南京理工大学机械工程学院,南京 210094;2 华安工业集团有限公司,黑龙江齐齐哈尔 161046)
炮口速度对弹丸飞行稳定性的影响
刘志林1,王雨时1,闻 泉1,张志彪1,刘锦春2,颜秀红2
(1 南京理工大学机械工程学院,南京 210094;2 华安工业集团有限公司,黑龙江齐齐哈尔 161046)
为了给引信弹道炸分析和火炮多级炮口速度设计提供弹道环境参考,建立弹丸攻角微分方程,分析了弹丸追随稳定性、尾翼弹静稳定性和旋转弹陀螺稳定性,得到描述变号装药火炮弹丸飞行稳定性的攻角与炮口速度的函数关系。结果表明:无论是尾翼弹还是旋转弹,对于同一火炮而言,在射角相同的情况下,炮口速度低的弹丸飞行稳定性不如炮口速度高的。此外,炮口速度为跨音速情况时,旋转弹丸飞行稳定性也不易保证。
外弹道学;理论分析;设计原则;飞行稳定性;攻角;弹道炸;引信安全性
0 引言
一般大、中口径地面压制火炮采用减装药实现炮口速度分级[1-2],不同的装药号对应不同的炮口速度。
查阅外弹道学及弹丸设计理论文献[2-17]发现,在研究炮弹外弹道飞行稳定性时,弹道参数采用的往往是全装药条件下的炮口速度,仅见文献[18]介绍了多级炮口速度弹丸的飞行稳定性设计原则,认为在飞行稳定性设计时,需考虑三种情况:最大炮口速度、最小炮口速度和炮口速度为跨声速的情况。“GJB 4225—2001《榴弹定型试验规程》”中的“规程301弹丸飞行稳定性试验”[19]仅规定以最大射角进行射击,并未说明炮口速度如何选取。事实上,对于同一火炮、同一弹种、同一射角,变号发射装药弹丸间飞行稳定性的差异可能与炮口速度有关。研究炮口速度对弹丸飞行稳定性的影响,有助于分析近年来地面压制火炮弹丸非全装药条件下频繁发生的引信弹道炸现象。文中以攻角来论述弹丸的飞行稳定性。
1 弹丸飞行动力学
1.1 弹丸的运动微分方程组
研究弹丸飞行稳定性,需要建立弹丸运动微分方程组[2,9]。为了简化问题,首先假设弹丸是轴对称的刚体;弹丸质心位于几何轴线。
作为刚体,弹丸的运动微分方程组可分为质心平动方程组和绕质心转动方程组。
弹丸的质心平动方程组可分为:表征速度大小变化的微分方程和表征速度方向变化的微分方程:
(1)


弹丸绕质心转动方程组可分为弹丸绕弹轴自转和弹轴摆动两部分:
(2)
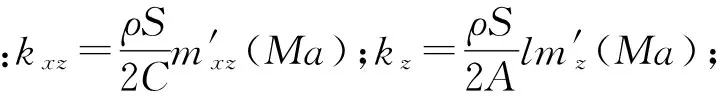

1.2 弹丸飞行稳定的动力系统
结合式(1)、式(2)和复攻角公式Δ=Φ-Ψ,并忽略两力矩乘积的高阶小量,得出弹丸飞行稳定性的攻角微分方程:
(3)
为了简化方程,引进新自变量弹道弧长s,且:
(4)
得到新的以弹道弧长s为自变量的攻角微分方程:
(5)
式(5)为一般炮弹飞行攻角二阶微分方程,可以作为研究弹丸飞行稳定的动力系统。即弹丸飞行稳定性问题可以转化为对应弹丸攻角微分方程解的稳定性问题。
2 炮口速度对弹丸飞行稳定性的影响
2.1 尾翼弹飞行稳定性分析
一般尾翼弹微旋。为便于研究,假设尾翼弹不旋转。作用在尾翼弹上的空气动力如图1所示。其中静力矩Mz与旋转弹丸静力矩方向相反,起到减小攻角的稳定力矩的作用。

图1 作用在尾翼弹上的空气动力
从式(5)中略去与旋转有关的力和力矩。由于不旋转,所以在单一初始扰动下,弹丸将做平面摆动。此时攻角可用实变量表示,即得尾翼弹的攻角微分方程:
(6)
由微分方程稳定性理论[20]可知,若被扰动的线性微分方程的非齐次项在s→+∞时是有界的,则微分方程的稳定性取决于其对应的齐次方程解的稳定性。因此,只需考虑式(6)对应齐次方程解的稳定性。

(7)

从式(7)可以得出:对于尾翼稳定弹丸,如果b>0、kz<0,则系统(6)就是静稳定的。又可知,随着弹道弧长的增加,攻角的幅值不断衰减,并作周期性摆动,因此系统(6)具有渐进稳定性。
对于非齐次项的特解,实际上就是在曲线弹道上,由于重力的作用使弹丸速度方向发生偏转,产生的滞后攻角。如果滞后攻角产生的稳定力矩能使弹轴转动,从而保持攻角较小,则该尾翼弹就具有追随稳定性。此滞后攻角称为动力平衡角,用δp表示:
(8)
弹丸的攻角微分方程是一个二阶变系数非齐次常微分方程。为了便于单独分析炮口速度对微分方程稳定性的影响,且由于气动系数在一定马赫数范围内变化不大,可以采用所谓“系数冻结法”[2],即以弹丸抛射初始升弧段为研究对象,近似认为各气动系数为常数,且θ几乎不变。
首先,分析静稳定性。将式(7)转化为攻角关于时间t的关系式。结合式(1)和式(4)可得:
(9)
求解后,得:
(10)
又由式(1)可得出速度与时间的关系式:
(11)
为了便于分析,式(7)又可表示为:
(12)

显然,δm0为最大攻角幅值,δm0与v0成反比。
下面讨论攻角摆动幅值衰减速度exp(-bs)与v0的关系:

(13)
由此可见,最大攻角幅值δm0随着v0的增大而减小,攻角摆动幅值衰减速度exp(-bs)随着v0的增大而加快。即炮口速度越大,尾翼稳定弹的静稳定性越好。
其次,分析追随稳定性。根据式(8)和式(11)易知,动力平衡角与炮口速度呈反相关,即炮口速度越大,尾翼弹追随稳定性越好。
除此之外,还需考虑一种特殊情况,即炮口速度为跨音速的情况。炮口速度为跨音速时,上述“系数冻结法”不再成立,此时气动系数突变,达到极大峰值,其他情况下变化较为平缓。再次考虑式(7),-kz、b均达到极大值,尾翼弹丸静稳定性比按“系数冻结法”给出的结果还要好;考虑追随稳定性式(8),-kz与bx+kzz对δp的影响可以抵消,因此,尾翼弹的追随稳定性与按“系数冻结法”给出的结果相比变化不明显。总之,尾翼弹炮口速度为跨音速时,弹丸的稳定性比按“系数冻结法”给出的结果要好。
综上所述:对于同一火炮、同一尾翼弹丸,在射角相同的情况下,炮口速度越大,弹丸稳定性越好;而炮口速度越小,弹丸稳定性越差。
2.2 旋转弹飞行稳定性分析
旋转弹阻心一般在其质心之前。静力矩Mz起到增大攻角的翻滚力矩的作用。图2为某旋转弹受到的空气动力示意图。

图2 作用在旋转弹上的空气动力
旋转弹丸攻角微分方程即式(5)。从中可以看出,由于作用在弹丸上的马格努斯力一般很小,只是升力的百分之几,所以可以略去不计,但是马格努斯力矩对弹丸稳定性影响较大,应予以考虑。


(14)
由微分方程解的稳定性可知,旋转弹丸陀螺稳定必要条件为:σ>0,结合上式可得该系统同样具有渐进稳定性。
采用“系数冻结法”,以弹丸抛射初始升弧段为对象,研究炮口速度对旋转弹丸稳定性的影响,由式(14)可知:
章动振幅是衰减的,其初始振幅[2,21]为:
(15)
式中:2e为弹炮径向间隙;Lb为导引部长度。
振幅衰减速度为:
(16)
尽管同一火炮不同装药级炮口速度不同,但火炮膛线终缠度η[2]是不变的:
(17)
将式(17)代入式(15)中得,δm0与v0成反比。2.1节已得出,s与v0呈正相关,结合式(16)易知,振幅衰减速度随v0增大而加快。因此,炮口速度越大,旋转弹陀螺稳定性越好,炮口速度越小,旋转弹陀螺稳定性越差。
其次,讨论对应非齐次解的稳定性,即追随稳定性。对于旋转稳定弹丸,重力使弹丸速度方向远离弹轴,陀螺稳定性则力图使速度与弹轴方向保持不变,这种弹轴追随速度矢量下降而下降的特性就叫旋转弹丸的追随稳定性,用动力平衡角δp表征。
(18)
式中h为压心到质心的距离。
结合式(11)和式(18)知,动力平衡角与炮口速度呈反相关,且炮口速度越大,动力平衡角衰减越快。
此外,同样需要考虑炮口速度为跨音速的特殊情况。炮口速度为跨音速时,气动系数突变,达到极大峰值,不再满足“系数冻结法”。重新修正旋转弹陀螺稳定性,根据式(15)、式(16)得,kz增大,初始振幅增大;一般情况下,kzz+by-kxz>0,因为kzz、by、kxz均达到极大值,所以振幅衰减速度增大。再考虑追随稳定性,kxz增大,δp幅度较小,衰减加快,即追随稳定性比按“系数冻结法”给出的结果要好。综上,旋转弹丸炮口速度为跨音速时,弹丸攻角炮口速度幅值较大,但衰减速度加快,稳定性应加以考虑。
综上所述:对于同一火炮、同一旋转弹丸,在射角相同的情况下,炮口速度越大,弹丸飞行稳定性越好;而炮口速度越小,弹丸飞行稳定性越差。此外,旋转弹丸炮口速度为跨音速情况下飞行稳定性不易得到保证。
3 试验验证
表1为某155 mm加榴炮榴弹地面密集度试验结果。表2为文献[18]根据某105 mm榴弹炮射击试验数据计算出的弹道顶点动力平衡角。两表中的发射装药编号顺序规律相反,系源自不同的参考文献。表3为[21]计算得到的某155 mm全膛弹的飞行稳定性特性。表4为某81 mm迫击炮弹配用不同火炮时的地面密集度试验结果,其中弹丸完全相同。

表1 某155 mm加榴炮榴弹地面密集度试验结果
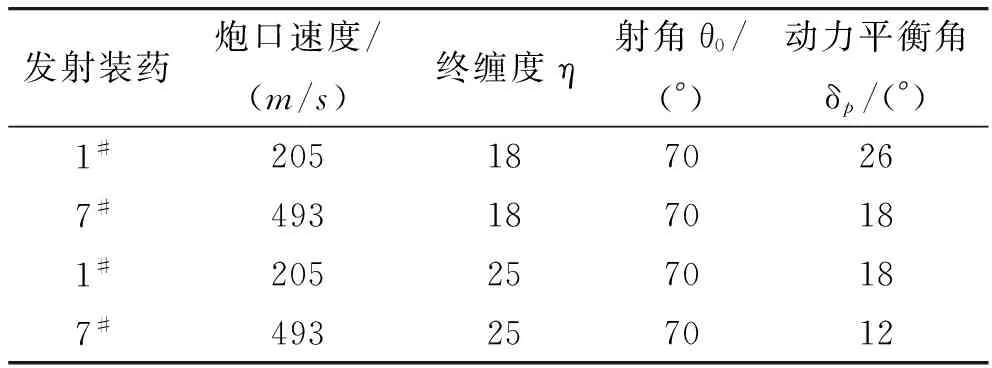
表2 某105 mm榴弹炮弹道顶点动力平衡角计算结果[18]

表3 某155 mm全膛弹的飞行稳定性特性[21]

表4 某81 mm迫击炮弹配用不同迫击炮时的地面密集度
弹丸地面密集度大小可在一定程度上反映弹丸飞行稳定性的优劣。弹丸飞行稳定性差,地面密集度不可能好。弹丸飞行稳定性好,地面密集度才有可能好。地面密集度好,弹丸飞行稳定性不可能不好。表1、表4中的弹丸最大射程地面密集度和表2、表3中的动力平衡角均可以反映弹丸的飞行稳定性特性,表3中的陀螺稳定因子Sg和动态稳定因子Sd满足1/Sg 在火炮、弹丸和射角相同的情况下,低炮口速度时的弹丸攻角初始振幅和动力平衡角要大于高炮口速度时的,而攻角衰减速率要小于高炮口速度时的,即低炮口速度时的弹丸飞行稳定性要比高炮口速度时的飞行稳定性差。对于可变发射装药而言,低炮口速度装药条件下的弹丸飞行稳定性要比高炮口速度装药条件下的弹丸飞行稳定性差。 炮口速度为跨音速条件下的旋转稳定弹丸飞行稳定性不易得到保证,而尾翼稳定弹丸则不存在此问题。 弹丸飞行稳定性计算和考核试验,不但要关注以往关注的高炮口速度情形如全装药,更要关注低炮口速度情形以及旋转弹丸炮口速度为跨音速的情形。 在火炮、弹丸和射角相同的情况下,因外弹道上弹丸章动或摆动过大所引起的引信弹道炸,在低炮口速度条件下的发生概率要高于高炮口速度条件下的发生概率。炮口速度为跨音速条件下的旋转弹丸因飞行稳定性不易保证,其引信可能也易发生弹道炸。 [1] 钱林方. 火炮弹道学 [M]. 北京: 北京理工大学出版社, 2009. [2] 韩子鹏, 赵子华, 刘世平, 等. 弹箭外弹道学 [M]. 北京: 北京理工大学出版社, 2008. [3] Я. M. ШAПИPO. 外弹道学 [M]. 李芳新, 译. 哈尔滨: 中国人民解放军军事工程学院, 1957. [4] 华恭, 欧林尔. 弹丸作用和设计理论: 榴弹和迫击炮弹 [M]. 北京: 国防工业出版社, 1975. [5] 美国陆军装备司令部. 弹丸的飞行稳定性设计 [M]. 杨为中, 译. 北京: 国防工业出版社, 1976. [6] 浦发. 外弹道学 [M]. 北京: 国防工业出版社, 1980. [7] 周效亮. 旋转弹丸的飞行稳定性设计 [J]. 兵工学报: 弹箭分册, 1983(2): 8-24. [8] 魏惠之, 朱鹤松, 汪东晖, 等. 弹丸设计理论 [M]. 北京: 国防工业出版社, 1985. [9] 董亮, 王宗虎, 赵子华, 等. 弹箭飞行稳定性理论及其应用 [M]. 北京: 兵器工业出版社, 1990. [10] 赵子华. 不对称因素引起射弹散布的分析与估算 [J]. 弹道学报, 1993, 18(4): 45-49. [11] 上官垠黎. 高超音速旋转稳定炮弹的阻力与稳定性分析 [J]. 弹箭技术, 1997(2): 27-35. [12] 徐明友. 现代外弹道学 [M]. 北京: 兵器工业出版社, 1999. [13] [俄]A. A. 德米特里耶夫斯基, Л. H. 雷申科, C. C. 波哥吉斯托夫. 外弹道学 [M]. 张莺, 韩子鹏, 薛晓中, 译. 北京: 国防工业出版社, 2000. [14] 吴宏, 赵有守. 随机因素对弹丸射击精度影响的分析方法 [J]. 弹箭与制导学报, 2001, 21(3): 56-59. [15] 徐明友. 高等外弹道学 [M]. 北京: 高等教育出版社, 2003. [16] 钱明伟, 王良明, 郭锡福. 火炮武器高原射击时的弹道特性研究 [J]. 弹道学报, 2009, 21(4): 21-25. [17] 翟英存, 陶国辉, 党明利. 尾翼稳定火箭弹高空气动力与弹道特性研究 [J]. 弹箭与制导学报, 2011, 31(2): 142-144. [18] 郭锡福. 火炮武器系统外弹道试验数据处理与分析 [M]. 北京: 国防工业出版社, 2013. [19] GJB 4225—2001榴弹定型试验规程[S]. 中国人民解放军总装备部, 2001. [20] 陆启韶, 彭林平, 杨卓琴, 等. 常微分方程与动力系统 [M]. 北京: 北京航空航天大学出版社, 2010. [21] 张靖. “枣核”弹稳定性及散布分析 [J]. 华东工学院学报, 1974(4): 169-180. [22] 刘锦春. 弹药系统总体设计思想和结构与性能特点 [G]∥火炮技术研究开发中心. 155 mm自行加榴炮武器系统论文集: 上册. 北京: 航空工业出版社2013: 374-382. The Influence of Muzzle Velocity on the Projectile Flight Stability LIU Zhilin1,WANG Yushi1,WENG Quan1,ZHANG Zhibiao1,LIU Jinchun2,YAN Xiuhong2 (1 School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2 Huaan Industries Group Co. Ltd, Heilongjiang Qiqihar 161046, China) In order to provide ballistic environment reference for analysis of fuze ballistic explosion and design of multi-level muzzle velocity of artillery, based on differential equations of projectile angle-of-attack, trailing stability of projectile, static stability of finned projectile and gyro stability of rotating projectile were analyzed, a function of angle-of-attack and muzzle velocity was discovered, while flight stability of charge-variable projectile can be described by angle-of-attack. The result indicates that whether finned projectile or rotating projectile, for the same gun and angle-of-fire, projectile flight stability of high muzzle-velocity is better than the lower one. In addition, as for transonic muzzle velocity, flight stability of rotation projectile is difficult to guarantee. exterior ballistics; theoretical analysis; design principles; flight stability; attack angle; ballistic explosion; fuze safety 2015-01-06 刘志林(1990-),男,安徽合肥人,硕士研究生,研究方向:弹药工程与引信技术。 TJ301 A4 结束语
