基于ISIGHT的导引头伺服控制系统参数优化方法
2015-03-04刘明锋吕鸿鹏
刘明锋,吕鸿鹏,李 杰,李 琳,常 磊,宋 哲
(中国兵器工业第203研究所,西安 710065)
基于ISIGHT的导引头伺服控制系统参数优化方法
刘明锋,吕鸿鹏,李 杰,李 琳,常 磊,宋 哲
(中国兵器工业第203研究所,西安 710065)
为了使导引头伺服控制系统各参数达到最优,提出了一种多参数优化设计方法。文中采用MDO技术,在ISIGHT软件环境下集成导引头多体动力学模型和控制系统模型,以时间误差积分(ITAE)作为优化目标,利用多岛遗传算法(MIGA)完成了对导引头伺服控制系统各参数的优化。仿真结果表明,采用该方法能够使导引头伺服控制系统具有更好的性能指标,具有很好的应用前景。
控制系统;多参数优化;MIGA优化;ISIGHT
0 引言
导引头伺服控制系统通常采用三环控制,每个环路采用PID控制或滞后超前的控制方式,涉及的控制参数较多,传统的控制器参数调整方法大多采用人工经验指导下的试凑法,这种方法很难使各参数在全局范围内达到最优。
多学科优化设计方法可充分考虑各参数之间的相互影响和耦合作用,通过迭代运算可进行多参数同时优化。文中以ISIGHT软件为基础,集成结构模型、动力学模型和控制模型,利用多岛遗传算法[1]为寻优手段,实现了导引头伺服控制系统参数优化。
1 参数优化集成平台建立
基于ISIGHT集成优化软件,通过二次开发建立了导引头伺服控制系统参数优化平台,参数优化流程如图1所示。导引头伺服控制系统参数优化涉及机械结构、动力学以及控制系统3种模型,各模型的建立分别采用UG、ADAMS、Matlab/Simulink完成[2]。

图1 导引头参数优化流程图
利用UG软件,通过参数化建模方法,建立导引头的三维几何模型,通过该模型可实现结构参数的自动加载和更新;UG设计结果作为ADAMS软件的输入,在ADAMS软件中加入载荷及运动约束,建立多体动力学模型;动力学模型作为控制模型的负载,接收Simulink发送的转矩命令进行相应运动,并将运动参数反馈给控制系统,ISIGHT根据优化目标和约束条件,利用选择的优化算法作为寻优手段,开展多个参数的优化工作。模型之间参数的传递和交互均由ISIGHT自动完成,无需人工干预。
2 仿真模型的建立
在导引头伺服控制系统参数优化过程中,为了实现控制模型与动力学模型的联合仿真,分别在Matlab和ADAMS当中定义相应的输入、输出变量,并将接口信息导出[3]。在ISIGHT软件环境下自动完成ADAMS与Matlab之间的参数传递,如图2所示。
伺服控制系统仿真模型,以导引头方位跟踪回路为参照,在Matlab/Simulink环境中建立角跟踪回路仿真模型,如图3所示。

图2 Matlab与ADAMS参数传递示意图
跟踪回路包括电流环、稳定环和跟踪环3个环路,电流环采用PI控制器,稳定环和跟踪环均采用滞后、超前校正方式,以降低系统带宽并加大相位余量。电流环控制器参数根据项目需求进行计算并单独仿真,将参数固定,不参与伺服控制系统整体参数优化。文中进行参数优化的变量为稳定环的5个变量和跟踪环的5个变量,共10个变量。
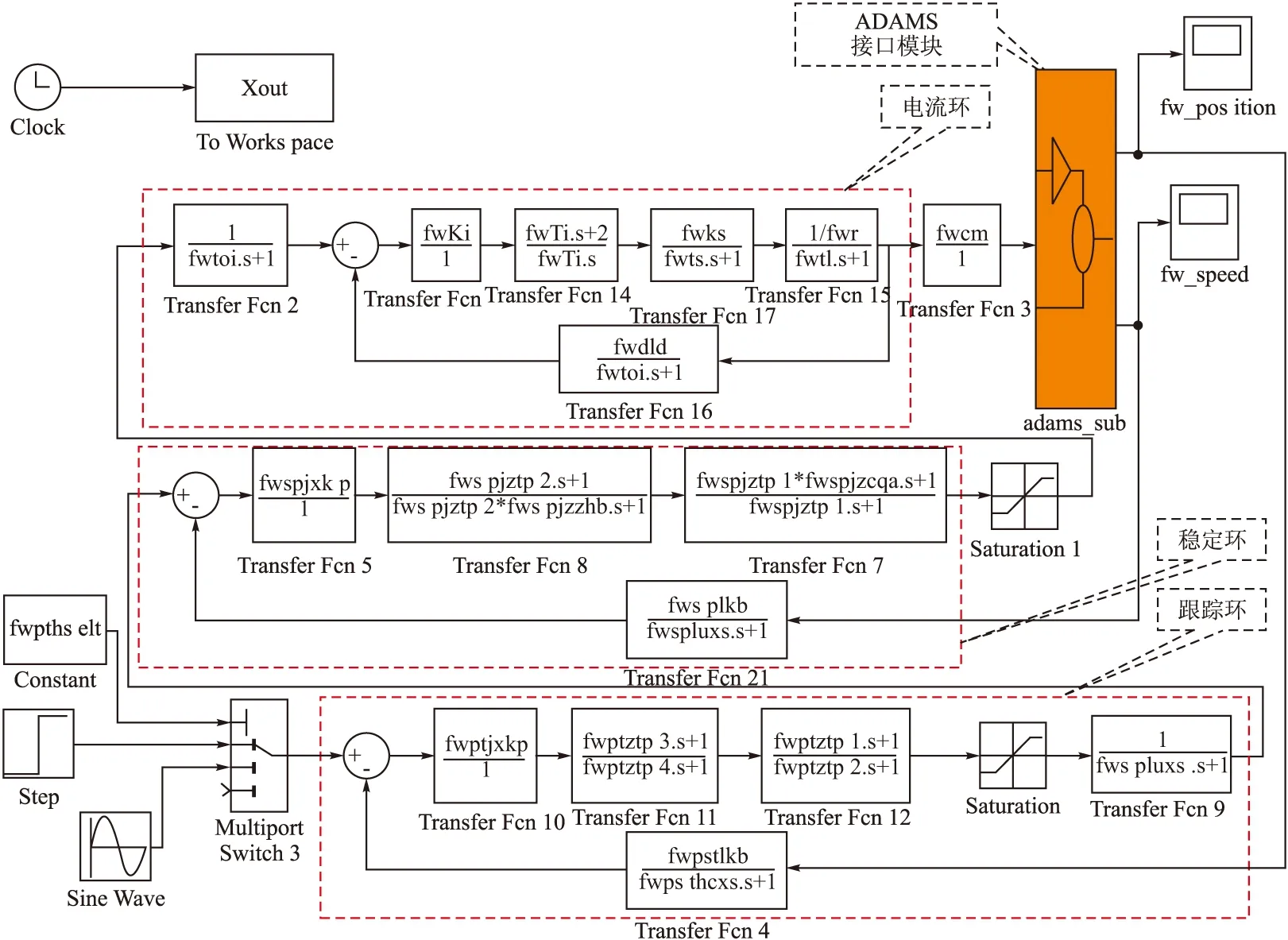
图3 导引头伺服控制系统仿真模型
在Simulink中,将代表ADAMS模型的adams_sub块放置到图3当中的平台及负载模块处,作为与ADAMS仿真通信的接口。动力学模型与控制模型之间形成闭合回路,实现两者之间的数据交换。进行仿真算法、仿真时间和求解步长等设置后,可对稳定平台在控制系统驱动下的运动过程进行仿真,并进行参数优化。伺服控制系统模型中各环路调节器参数均以变量形式表示,仿真过程中在ISIGHT软件驱动下,完成参数的自动更新。
3 参数优化模型
3.1 优化变量
文中以方位通道为例,对稳定环路和跟踪环路的参数进行优化。稳定环路和跟踪环路均采用滞后、超前的校正方式,需要优化的变量主要包括放大系数、转折频率、滞后超前因子等共计10个变量,如表1所示。
3.2 优化目标函数
为了能够综合地反映出系统调节动态过程的整体性能,采用时间误差积分(ITAE)[4]作为系统优化目标函数,如式(1)所示。
(1)
式中:t为仿真时间;e(t)为偏差。该目标函数对瞬态响应后期的偏差有较好的控制能力,用该指标优化的系统,一般超调量小,而且系统比较稳定。优化目标:JITAE最小。

表1 变量及优化结果
3.3 约束条件
为了使系统动态响应过程“快”和“稳”,并防止运动过程有大的超调,设置超调量和系统调节时间为约束条件。
3.4 优化模型的建立
通常控制器参数与系统动态性能指标之间呈现复杂的函数关系,有些在理论上就是不连续的[5],因此在求解此类优化问题时,基于导数的优化算法并不适用。而遗传算法是模仿生物进化过程中的遗传繁殖机制,对优化问题解空间的个体进行编码(二进制或其他进制),然后对编码后的个体种群进行遗传操作(如:选择、交叉、变异等),通过迭代从新种群中寻找含有最优解或较优解的组合,该算法不依赖于梯度,并且具有全局寻优能力,稳定性和适用性更强[6]。多岛遗传算法(MIGA)是对并行分布遗传算法(PDGAs)的改进,具有比传统遗传算法更优良的全局求解能力和计算效率,文中采用MIGA进行伺服控制系统的参数优化。将仿真模型和优化算法结合得到伺服控制系统参数优化模型[7],如图4所示。

图4 优化模型结构
4 参数优化及仿真
以阶跃和斜坡信号作为伺服控制系统的输入,以调节时间和超调量作为设计目标,采用试凑法来确定稳定环和跟踪环的调节器参数,即凭借经验和仿真结果来手动调节设计变量。经过尝试,采用如表1所示试凑法各变量参数,得到较为理想的动态调节过程,如图5所示,系统阶跃响应,超调量约为17%,调节时间0.25 s;跟踪5°/s匀速运动目标,最大跟踪误差0.16°/s;系统稳态时约有3%的波动,反映到视线角速度上,也就是视线角速度最大约有3%的误差。

图5 试凑法获得的系统响应

图6 利用优化算法获得的系统响应
利用文中所述方法进行参数优化设计,各设计变量优化区间及结构如表1所示。设置约束条件:调节时间小于0.15 s;超调量不大于20%。在ISIGHT软件中选择多岛遗传算法作为寻优手段,并设置子群规模、岛的个数、进化代数、交叉概率和变异概率等相关参数,在优化算法驱动下,ISIGHT软件自动进行参数的循环迭代和联合仿真,完成伺服控制系统各参数的优化。采用如表1所示的优化结果进行仿真,结果如图6所示,系统阶跃响应,超调量约为4.5%,调节时间小于0.1 s;跟踪5°/s匀速运动目标,最大跟踪误差0.04°/s;稳态时系统波动小于1%,也就是视线角速度误差小于1%。导引头性能明显优于图6所示动态响应过程。参数寻优过程如图7所示。

图7 参数寻找优过程
5 结论
文中通过在ISIGHT软件环境下集成导引头三维机械模型、多体动力学模型和控制系统模型,建立了导引头伺服控制系统参数优化框架和优化模型,并采用多岛遗传算法(MIGA)实现了导引头伺服控制系统
参数的优化。优化结果表明,文中的优化方法效果明显,提高了导引头伺服控制系统的性能,具有一定的工程使用价值。
[1] 赖宇阳, 姜欣, 方立桥, 等. Isight参数优化理论与实例详解 [M]. 北京: 北京航空航天大学出版社, 2012.
[2] 赵玉麟, 张崇军, 张虎子. 基于ADAMS和Matlab的导引头机电系统仿真 [J]. 弹箭与制导学报, 2009, 29(4): 77-79.
[3] 刘晋霞, 胡仁喜, 康士廷. ADAMS2012虚拟样机从入门到精通 [M]. 北京: 机械工业出版社, 2013.
[4] 胡寿松. 自动控制原理 [M]. 北京: 科学出版社, 2002.
[5] 吴麒, 王诗宓. 自动控制原理: 上册 [M]. 北京: 清华大学出版社, 2006.
[6] 郑佳焜, 杨雅君, 廖瑛. 基于遗传算法的导弹控制系统设计与仿真 [J]. 弹箭与制导学报, 2014, 34(5): 33-36.
[7] 贾清虎, 张红刚, 王辉. 稳定平台控制器参数多目标优化 [J]. 电光与控制, 2012, 19(4): 76-80.
A Method of Parameter Optimization for Control System of Missile Seeker Based on ISIGHT
LIU Mingfeng,LYU Hongpeng,LI Jie,LI Lin,CHANG Lei,SONG Zhe
(No.203 Research Institute of China Ordinance Industries, Xi’an 710065, China)
In order to realize optimization of all parameters for control system of missile seeker, a multi-parameter design and optimization method was proposed. With the technology of MDO, the associated model of mechanical system and that of control system of seeker were integrated based on ISIGHT, and time-error integral (ITAE) was adopted for optimization, parameter optimization was carried out for control system of seeker using multi-island genetic algorithm. The results of simulation demonstrate that performance of control system of seeker has been improved by this method, which shows that this method is promising for application.
control system; multi-parameter optimization; MIGA optimization; ISIGHT
2015-01-08
刘明锋(1979-),男,河南商丘人,高级工程师,研究方向:光电工程,伺服控制系统。
TJ765.3
A
