基于Matlab的古塔倾斜数据分析及监测

汤 志 浩

(河南工业职业技术学院 基础部， 河南 南阳 473009)



基于Matlab的古塔倾斜数据分析及监测

汤 志 浩

(河南工业职业技术学院 基础部， 河南 南阳 473009)

利用Matlab对某古塔1986年、1996年、2009年和2011年的观测数据进行了分析，依据观测数值，找出了古塔每层的中心点 ，对古塔的扭曲、弯曲、倾斜等进行了分析，得出了随着时间的推移，古塔的变形程度会进一步增加的结论.

古塔； 倾斜； 弯曲； 扭曲

文物是国家不可再生的文化资源，尤其是有上千年历史和文化的古塔，更是我们国家需要重点保护的古建筑.长期以来因各种因素的影响，古塔可能发生如倾斜、弯曲、扭曲等形变.对古塔的这些变形数据进行分析和预测，对我国文化遗产的保护具有重要的意义.本文试用Matlab对这些数据进行分析.

1 问题提出

长期以来，古塔因为自身重力、寒暑交替、风化等各种因素的影响，偶尔还可能遭受地震、飓风等自然灾害的破坏，可能发生如倾斜、弯曲、扭曲等各种损坏性形变.为了保护沉淀了上千年厚重历史、文化的古塔，文物管理部门会定期观测古塔，记录不同时期的变形数据，以根据数据拟定合适的保护方案.

某地区有一年代久远的古塔，属于国家重点保护的古建筑.某测绘公司按照文物管理部门的要求对该塔进行了4次观测，分别是1986年7月、1996年8月、2009年3月和2011年3月.依据对古塔四年的观测数据，本文将对三个问题进行探讨.

问题1：依据观测数值，找出古塔每层的中心点，并给出通用的方法，且将古塔每层中心点的坐标用表格列出来.

问题2：根据观测值对古塔的扭曲、弯曲、倾斜等变形程度进行分析.

问题3：结合问题1和问题2，分析和预测古塔的变形趋势和方向.

2 问题分析

依据1986年观测数据，在Matlab软件中做出三维曲线图[1]，见图1.

图1 由1986年数据得到的三维曲线

从图1可以看出，该古塔为八角形，共有13层，外加一个塔尖层，各层的八个观测点刚好取在古塔的八个角上.

2.1 模型的假设

(1)古塔初建成时，假设每层都与地面平行，八个测试点均在同一高度(z轴坐标相同)，且都在每层的地面上.

(2)在条件(1)的前提下，假设古塔的每层中心均在同一z轴上，即每层中心的x,y坐标相同(因为同一层八个观测点的z值变化很小).

(3)假设在建塔时塔身严格垂直于大地的水平面，则分析该塔时可把塔看作标准的八台，所以在建造时塔的八条棱等长.

(4)假设各层的观测点都取在古塔的地面上，而不是在中间的某个点.

(5)假设古塔初建成时，没有扭曲、弯曲、倾斜、下沉等现象.

(6)本文均以1986年的观测数据作为基准考虑.

2.2 问题1模型的建立与求解

该部分要求依据观测数据，将古塔每层的中心点找出来，并给出通用的方法，且将古塔每层中心点的坐标用表格列出来.本文取1986年第一层的八个观测数据进行具体计算和分析，数据见表1.

表1 1986年第一层八个点的横纵竖坐标 m

由表1可知，z坐标的数据基本接近，因此，可将1986年第一层中心位置的竖(z)坐标取这八个点的平均值，为1.78700，然后用Matlab软件做出这八个观测点的x,y(即横纵坐标)的散点图[1]，如图2所示.

图2 1986年观测到的第一层数据的散点图

图1的散点图，可用一个圆来拟合，如图3所示.

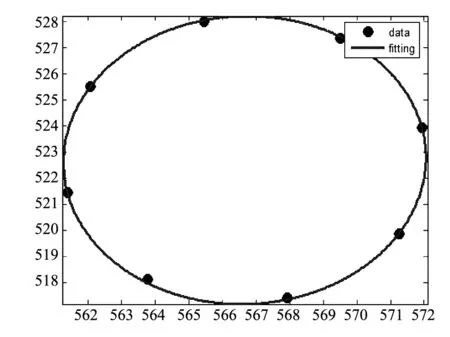
图3 第一层数据拟合图

在Matlab软件中调用circfit函数[2]可求出拟合圆的圆心的横纵坐标和半径，由表1的数据得到的结果如下：

xc=566.65180，

yc=522.69640，

R=2.83090.

其中，xc表示1986年第一层数据拟合圆圆心的横坐标；yc表示1986年第一层数据拟合圆圆心的纵坐标；R表示1986年第一层数据拟合圆的半径.

因此，由表1可以得出，1986年古塔第一层中心点的横纵竖坐标为：(566.65180，522.69640,1.78700).1986年所有观测点的平面俯视图如图4所示.

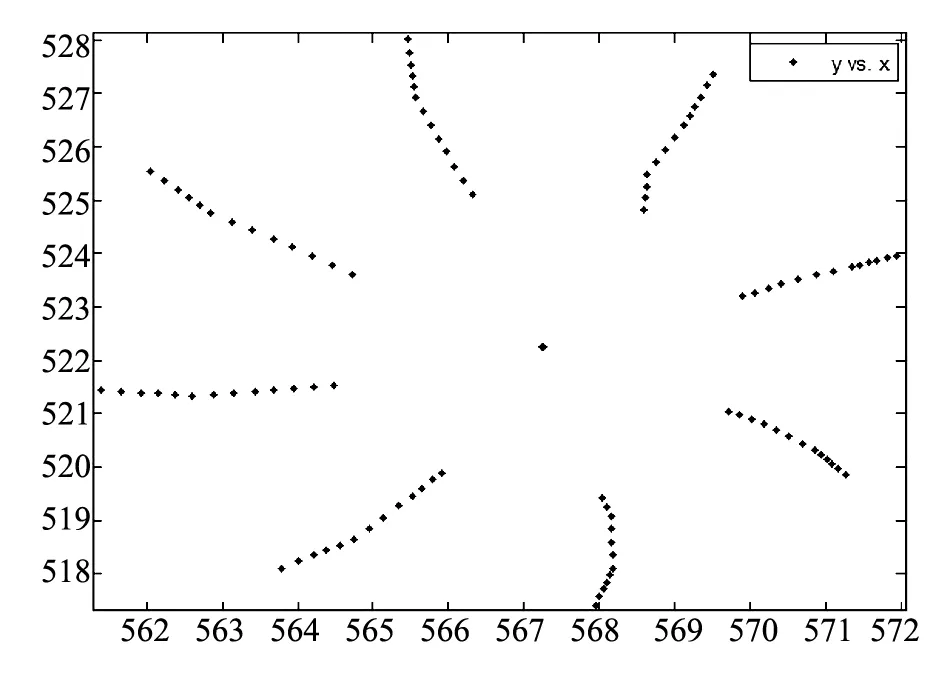
图4 1986年观测点的平面俯视图

观察图4可以看出，每一层上的点都可以用一个圆来拟合，因此，对于1986年观测的其他12层和塔尖，以及另外三年中的观测数据全部可以采用上面的方法将古塔各层中心点的坐标确定出来.表2-表5给出了四年中各层中心点的坐标数据.

表2 1986年每层中心点的横纵竖坐标 m

表3 1996年每层中心点的横纵竖坐标 m

表4 2009年每层中心点的横纵竖坐标 m

表5 2011年每层中心点的横纵竖坐标 m

2.3 问题2模型的建立与求解

2.3.1 倾斜

倾斜是指整体发生偏离竖向或者水平方向的偏斜.对于本题来说就是古塔偏离竖直方向的角度[3]，图5为1986年中心点的散点图.

图5 1986年中心点的散点图

由图5可以看出，中心点基本在一条直线上，因此，本文以古塔中心线偏离竖直方向的角度作为古塔的倾斜角度.先取塔尖和第一层的中心点来进行探讨.

再次，把四年的测量数据分别代入公式可得古塔四次测量时的倾斜角，见表6.

表6 四次观测时古塔的倾角

2.3.2 弯曲

构件(经常是线状构件)在外力作用下与中轴线偏转的状态称为弯曲.

先将问题1求出的结果即四次观测的各层中点在Matlab中拟合出曲线，并将其方程列出，然后用曲率公式算出四种情况下的曲率作为古塔的弯曲值(曲率是反映曲线偏离直线程度的量).

在Matlab中用三元线性回归[4]拟合出四条曲线如图6所示.

图6 四年中八个中心点的拟合图

曲线方程如下：

f1(x)=p1*x^5+p2*x^4+p3*x^3+p4*x^2+p5*x+p6.

p1=-4.476，p2=1.068e+004，

p3=-9.828e+006，

p4=4.279e+009，p5=-8.464e+011，p6=5.438e+013.

f2(x)=p1*x^5+p2*x^4+p3*x^3+p4*x^2+p5*x+p6.

p1=-6.88，p2=7003，p3=4.149e+006，

p4=-8.16e+009，p5=3.697e+012，p6=-5.5e+014.

f3(x)=p1*x^5+p2*x^4+p3*x^3+p4*x^2+p5*x+p6.

p1=-1.182，p2=3545，p3=-4.239e+006，

p4=2.528，p5=-7.518e+011，

p6=8.923e+013.

f4(x)=p1*x^5+p2*x^4+p3*x^3+p4*x^2+p5*x+p6.

p1=-4.476，p2=1.068e+004，p3=-9.828e+006，p4=4.279e+009,p5=-8.464e+011，p6=5.438e+013 .

曲率能体现出曲线对直线的偏离程度.在数学上通常用来反映曲线在某个点处的弯曲幅度.曲率取值越大，曲线弯曲越厉害.因此，本文可以通过计算四条曲线的曲率，使用Matlab软件计算出各层的弯曲角.结果见表7.

表7 各塔层三次测量的转角 弧度

2.3.3 扭曲

几何体因为外力作用发生横截面方向的顺(逆)时针扭转的变形状态称为扭曲，从第一层开始几乎每一层和其上一层都会有微小的倾角，这些小的角度加起来就是扭转角度，图7为1986年观测点对角线连线的俯视图，如果没有扭转，这些对角线的俯视图应该重合在一条线上，而这些对角线连线的俯视图呈分散状态，说明古塔的扭曲可以用图中八个分支的角度中最大的那个角度作为古塔的扭曲度.而且，随着年份的增加，古塔的扭曲程度会越来越大.

图7 1986年观测点对角连线俯视图

通过在Matlab中对数据的处理，给出了四年中对角线在水平面上投影产生的倾斜度的最大值，即古塔的扭曲度,见表8.

表8 古塔扭曲角度 弧度

2.4 问题3求解

问题3为分析该古塔的变形趋势.从问题2的求解可以看出，古塔在四次测量倾角时，与z轴的夹角都达到了4.2度，这个角度随着各种因素的作用会进一步变大.由图7可以看出，整个塔身呈现顺时针旋转的扭曲状态，四年中古塔在顺时针方向上转动的角度由0.0135变为0.0139，扭转角度增加.而且由图4可知，观测点在左上角分布稀疏，右下角分布密集，这表明古塔在东南角有下沉的变化趋势.从图6对四年古塔的各层中心点的描绘可以看出，古塔的弯曲、扭曲、倾斜在各层、各个方向都存在.因为长期受自身重力、寒暑交替、风化等各种因素的影响，偶尔还要遭受地震、飓风的破坏，古塔的弯曲角度、扭曲角度、倾斜角度、下沉趋势，如果不人为保护的话，都会进一步变大.

图8是以1986年的数据为例做出的古塔第三层底面的三维图，它进一步证明了对古塔的扭曲、弯曲、旋转、倾斜、下沉的变化趋势分析是正确的.

3 模型的评价与改进

(1)在问题1中用圆来拟合，取圆的中心作为古塔各层的中心位置，这在将来的研究中可以采用椭圆拟合，这样会更具有一般性，因为圆是椭圆的特例.

(2)运用Matlab和Excel软件画图，进行函数调用和编程求解，产生的误差较小，结果准确、合理.

图8 1986年古塔第三层底面三维图

(3)采用函数拟合法建立的模型原理简单，符合实际，简化了算法，计算方便.

(4)所建模型和使用的方法通用性强，对类似的问题均有较强的参考意义.

(5)在计算中心坐标和扭转角度时充分运用了垂直投影的数据处理方法.

[1] 颜文勇.数学建模[M].北京：高等教育出版社，2011：160-163.

[2] 张志涌,杨祖樱.Matlab教程[M].北京：北京航空航天大学出版社，2010：130-135.

[3] 胡志晓.古塔倾斜观测和数据分析[J].江苏建筑,2011(6):34-44.

[4] 韩中庚．数学建模方法及其应用[M].北京：高等教育出版社，2009:122-123.

责任编辑：金 欣

The Matlab-based data analysis of an ancient tower

TANG Zhi-hao

(Department of Basic Teaching, Henan Polytechnic Institute, Nanyang, Henan 473009, China)

This study is based on the Matlab-based data analyses of a tower in 1986, 1996, 2009 and 2011 in relation to the center point of each of the ancient tower, distortion of the ancient tower, bending, and tilting.

ancient tower; tilting; bending; distortion

2015-05-27

汤志浩 (1980-)，女，湖北十堰人，河南工业职业技术学院讲师，硕士，研究方向：应用数学.

1009-4873(2015)04-0015-06

O242.1

A