基于优化FGRBF神经网络的机器人跟踪控制

陆 薇， 樊劲辉， 张红瑞

(1.石家庄医学高等专科学校 计算机系，河北 石家庄 050071；2.河北科技大学 电气工程学院，河北 石家庄 050018；3.石家庄职业技术学院 信息工程系，河北 石家庄 050081)



基于优化FGRBF神经网络的机器人跟踪控制

陆 薇1， 樊劲辉2， 张红瑞3

(1.石家庄医学高等专科学校 计算机系，河北 石家庄 050071；2.河北科技大学 电气工程学院，河北 石家庄 050018；3.石家庄职业技术学院 信息工程系，河北 石家庄 050081)

针对常规基于S型基函数的模糊神经网络存在随模糊控制规则数目增加导致中间层节点激增的问题，设计了一种改进型的模糊高斯径向基函数神经网络控制器，给出了优化的模糊神经网络结构模型和控制器设计优化改进方法，利用减少中间层节点的数量降低算法的复杂度，并提高跟踪控制的实时性.通过优化算法在移动机器人上的仿真应用，验证了所提改进算法在跟踪控制运行中的实时性、有效性和可行性.

模糊神经网络; 模糊高斯径向基函数; 移动机器人; 跟踪控制

在自主移动机器人的运动模型已知的前提下，用于轨迹跟踪的控制器通常可以采用基于精确模型的方法进行描述[1].但移动机器人运行过程中所处环境参数复杂，轨迹跟踪控制过程中，存在着诸多未知及不确定因素，如移动机器人与地面之间的粘性摩擦系数及重心的实时变化等.

为解决跟踪过程中存在的不确定性、非线性等问题，最优控制、模糊控制以及神经网络控制算法等已经在自主移动机器人领域广泛应用.模糊控制技术和神经网络控制技术由于无需建立系统的精确数学模型，适用于复杂环境下的线性、非线性及不确定性系统.对于模糊控制而言，若要实现在模糊控制器的设计过程中能够对输入和输出数据的增益参数，隶属度函数的数目，每个隶属度函数的宽度及控制规则、数量等的合理选择，需要设计者具有丰富的经验.近年来，神经网络与模糊控制相结合的方法在控制领域得到了普遍的关注和研究[2-10].而其中的模糊高斯径向基函数(FuzzyGaussianRadialBasisFunction，简称FGRBF)神经网络属于一类不依赖精确数学模型的算法，其本质上是模糊控制与神经网络的结合，且兼具两者的优点.利用神经元构成网络后所具备的自主学习功能，神经模糊网络能够实现模糊规则及隶属度函数的自主调节.因此，在对常规FGRBF神经网络进行分析的基础上，将传统的FGRBF网络结构进行优化，并在保证控制精度的条件下降低运算的复杂度，实现对自主移动机器人轨迹的跟踪控制，对进一步改善控制的实时性具有重要意义.

1 模糊高斯基函数神经网络的优化

1.1 模糊规则的简化

简化的模糊控制规则生成方法可视为模糊控制规则的一类特例[4].该简化算法在两种情况下成立，即模糊规则的后件为常数和模糊规则后件在模糊集合运算时为极小值.据此原则，将控制规则写成：

Ri:Ifx1=Ai1and…andxn=Ain，

(1)

thenu1=Bi1and…andup=Bip.

其中，x1，…，xn表示模糊控制的输入变量；u1，…，up表示模糊控制器的输出变量；Ri表示第i条模糊控制规则；Aij表示在第i条控制规则中与第j个输入变量对应的模糊集合的前件；Bij表示在第i条控制规则中与第j个输入变量对应的输出规则,此处的“前件”和“后件”通常也称为模糊规则的“条件部分”和“操作部分”.因此，模糊控制器的输出可表示为：

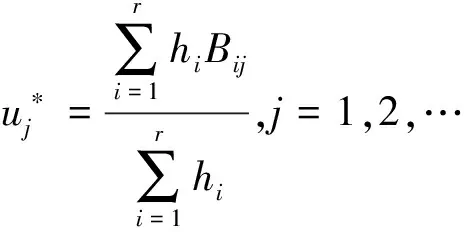
(2)

其中，hi=μAi1(x1)·μAi2(x2)…μAin(xn)，表示第i条模糊规则的适用度；μAik(xk)为第i条模糊规则中相对于第k个输入模糊变量的隶属度函数值，k代表1～n中的任意值.

1.2 隶属函数的计算

通常采用S型基函数的模糊神经网络，其中间层节点的数目会随着模糊控制规则数目的增加而大幅上升[4-5]，将FGRBF选取为式(3)的形式.

f(x)=eln(0.5)·x2.

(3)

双输入、单输出情况下的模糊高斯径向基函数神经网络控制器的结构如图1所示.

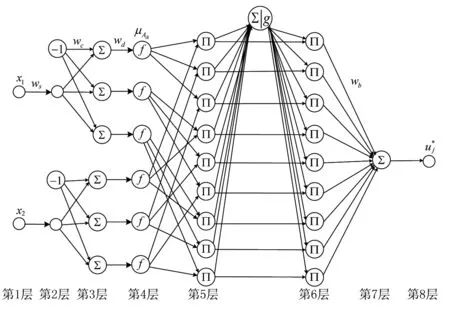
图1 优化的FGRBF神经网络结构

因此，进一步考虑网络中的节点间权值，将高斯径向基函数设定为：

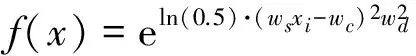
(4)

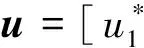
1.3 改进FGRBF网络的训练算法

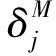
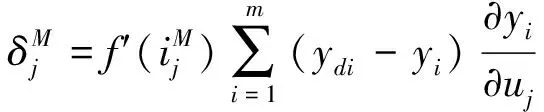
(5)

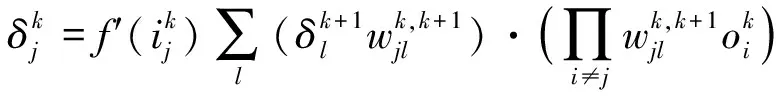
(6)

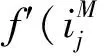
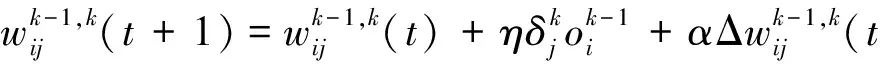
(7)

其中，η为学习率，α为稳定因子.式(7)用于调整权值参数wc，wd及wb，以提高权值计算的精度.由于ws为输入信号的归一化权值参数，其取值的变化范围较大，因此，ws的权值计算按式(8)进行：

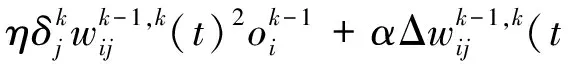
(8)

2 移动机器人模型及控制器设计

2.1 移动机器人的运动模型

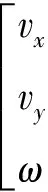
(9)

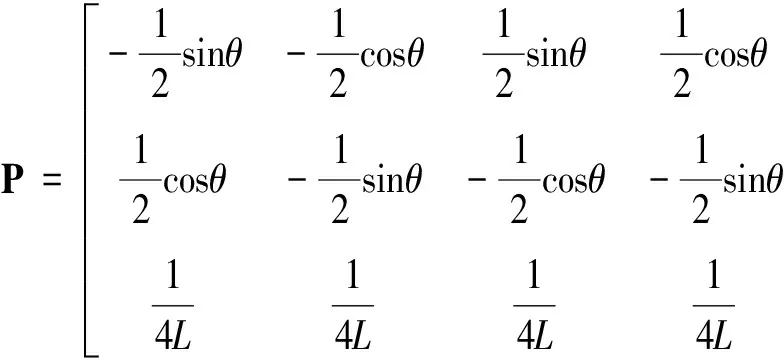
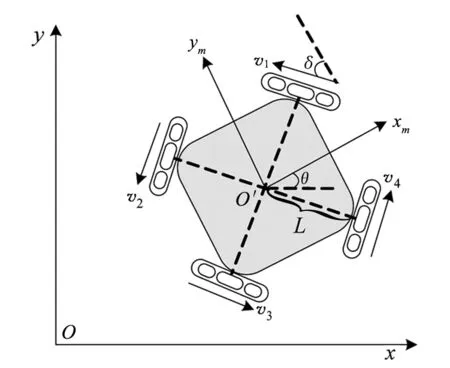
图2 四轮独立驱动全向机器人运动学模型

2.2 FGRBF控制器的设计

由式(9)可知,移动机器人行进速度和位姿朝向调整取决于四轮的输出转速组合，为多输入、多输出(MIMO)系统，故选用三个FGRBF神经网络控制器分别控制三个控制量，其控制结构如图3所示.

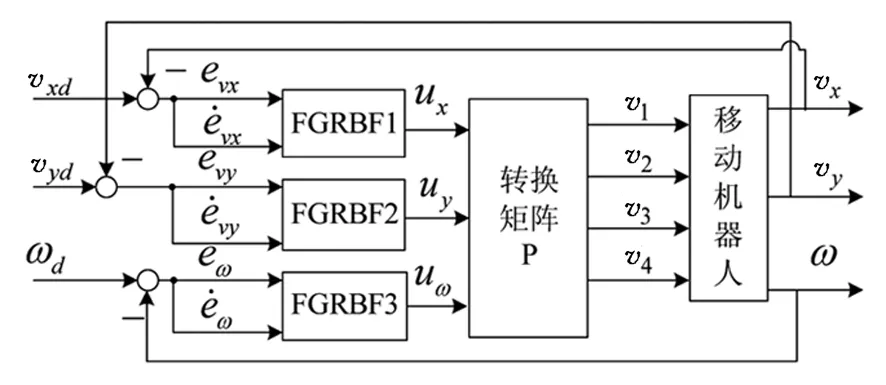
图3 FGRBF神经网络控制器结构

图3中vxd，vyd，ωd为系统的设定值输入量；控制器FGRBF1，FGRBF2，FGRBF3的输入均为二维形式；输出量分别为ux，uy和uω；P为转换矩阵.

3 仿真结果及分析

将FGRBF网络用于移动机器人的跟踪仿真试验中，分别选取三个FGRBF网络为控制器，其中，FGRBF1和FGRBF2的输入分别为移动机器人的两坐标轴方向的速度分量，为简化网络并提高运算的实时性，可选择相同的参数；FGRBF3中参数的选取参考前两个网络的参数.控制器相关参数选择如下：

机器人结构尺寸参数L=0.4 m；初始朝向角误差θ=3°；FGRBF网络中，训练迭代次数Tn=300；对速度和角度变化率两类网络的学习率ηv=0.002，ηω=0.001；考虑到安全性，对行进速度和朝向角变化率设定阈值，即v≤0.2 m/s和ω≤0.5 rad/s；FGRBF迭代终止误差E=0.01；跟踪总时长Ts=230 s；选取椭圆形轨迹进行跟踪仿真试验，椭圆轨迹方程为x2/a2+y2/b2=1,其中，a=2,b=1.

图4和图5分别给出二维平面上的跟踪轨迹及x,y轴方向上的位置跟踪轨迹.依据仿真结果可知，改进的FGRBF控制算法在轨迹跟踪过程中能实现完全跟踪且稳态误差终值为0.图6和图7分别给出了算法改进前后的跟踪控制位置误差及角度误差变化的对比.图8给出了网络的学习迭代过程误差变化，改进的FGRBF控制器经过约90次的学习，迭代误差迅速衰减至设定范围，因此，改进网络具有良好的收敛性.

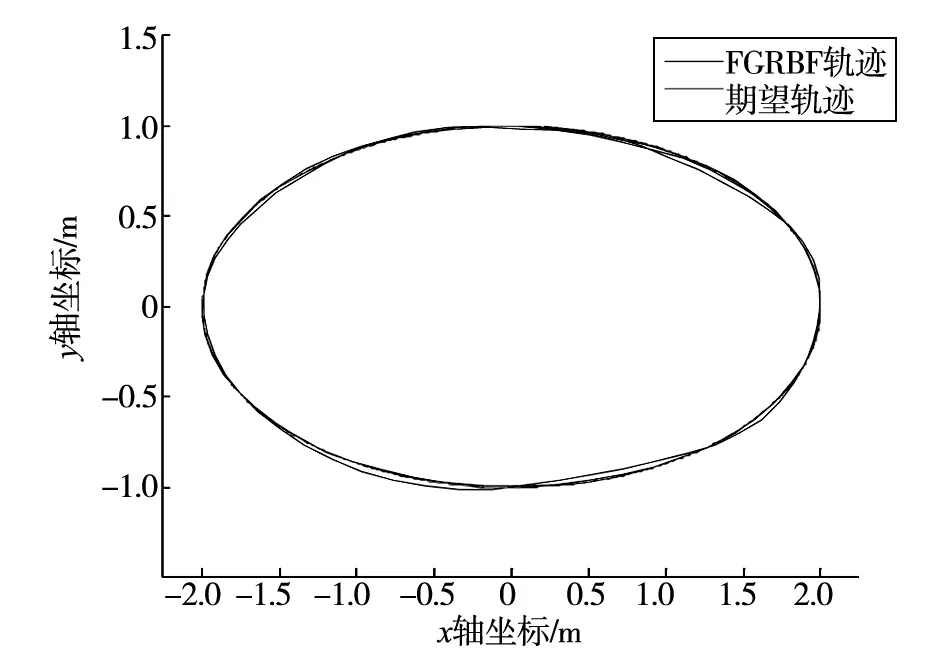
图4 基于FGRBF神经网络控制器的轨迹跟踪

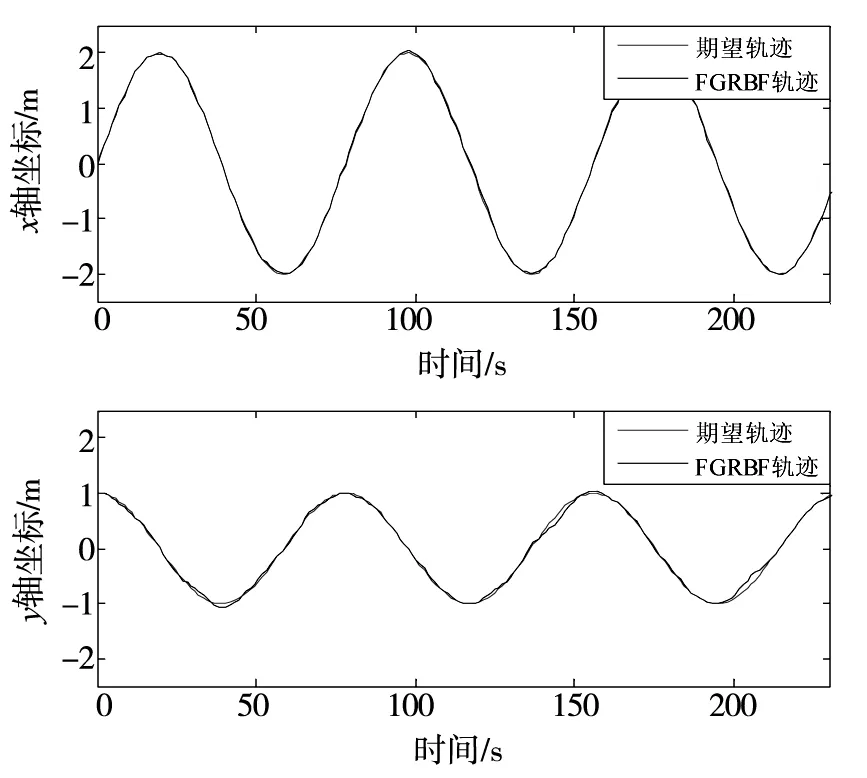
图5 基于FGRBF神经网络控制器x,y轴向位置跟踪

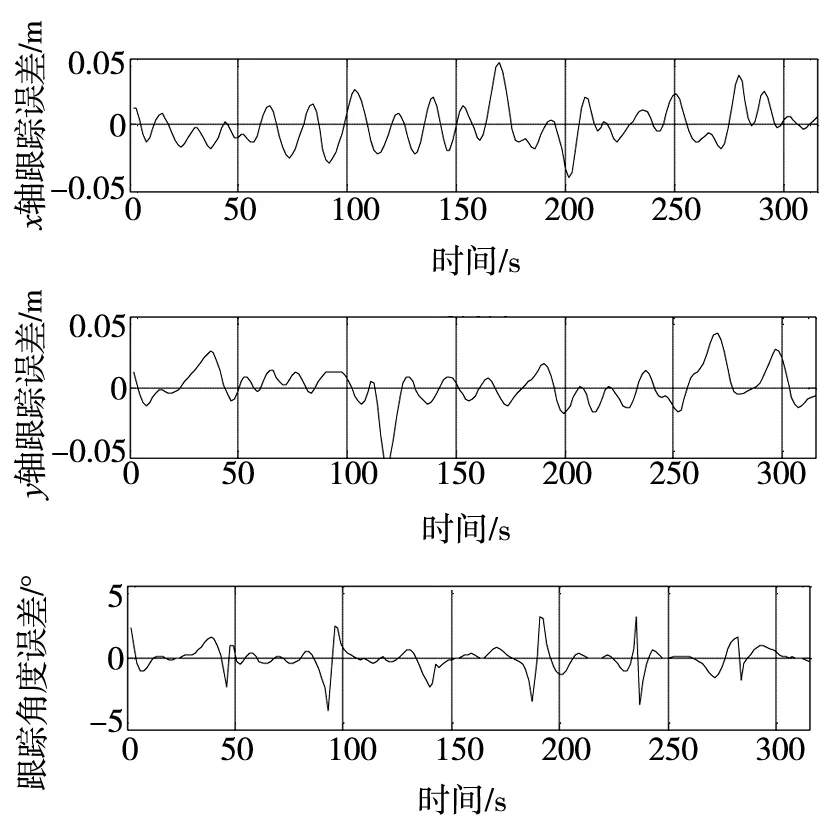
图6 改进前FGRBF神经网络控制器的跟踪误差

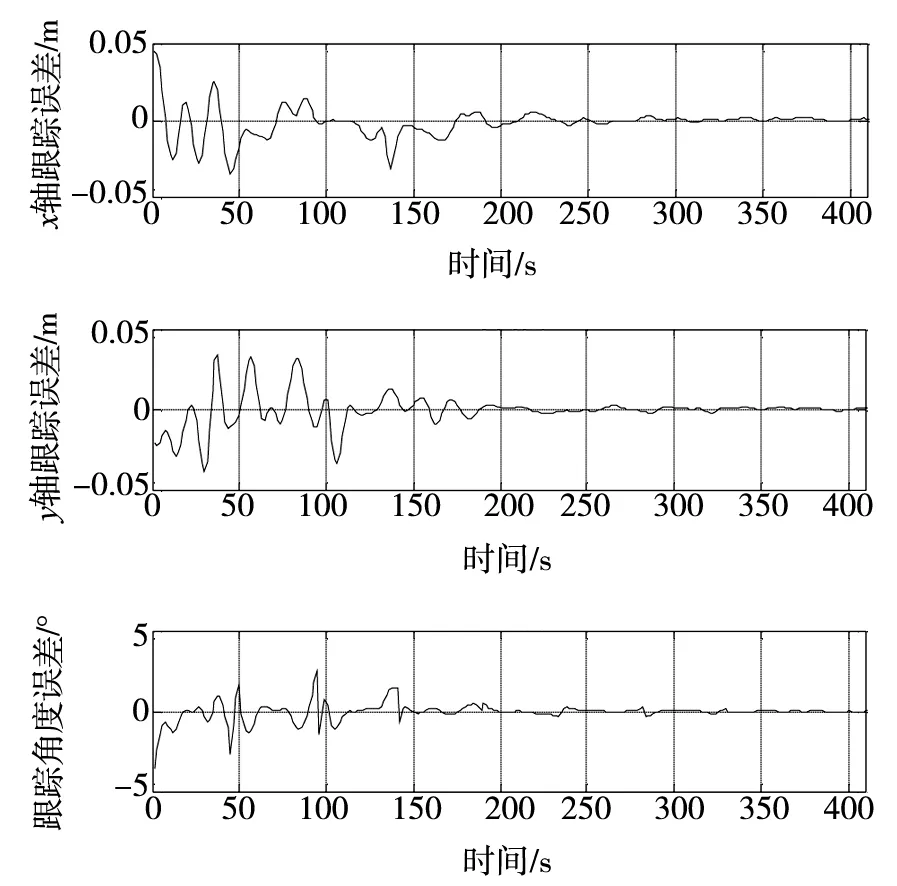
图7 改进后FGRBF神经网络控制器的跟踪误差

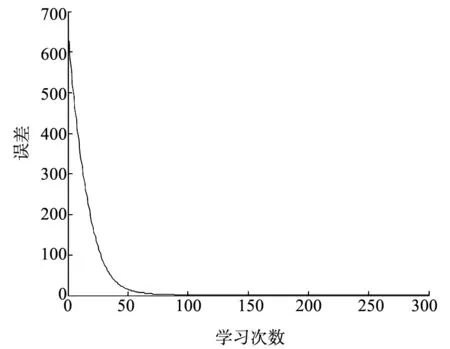
图8 改进后的FGRBF神经网络训练学习过程

4 结语

针对常规FGRBF神经网络中间层节点随模糊规则增加而激增的问题，分析并设计了改进型的高斯径向基函数神经网络，通过简化网络结构实现了降低算法复杂度并提高运行实时性的目的；同时，将其用作移动机器人跟踪控制的控制器，进行了椭圆形轨迹的跟踪控制仿真试验，通过对仿真结果的跟踪性能分析，证明了改进型网络控制器具有良好的学习收敛性，仿真结果充分验证了所设计算法在轨迹跟踪控制中的运行实时性和控制有效性.

[1] WATANABE K,TANG JUN,NAKAMURA M,et al.A fuzzy-Gaussian Neural Network and Its Application to Mobile Robot Control [J].Control Systems Technology,IEEE Transactions on,1996,4(2):193-199.

[2] CHEN YUN,ZHENG WEIXING,XUE ANKE.A New Result on Stability Analysis for Stochastic Neutral Systems [J].Automatica,2010,46(12):2100-2104.

[3] 孙洪淋,孙炜,石玉秋，等.基于模糊高斯基函数神经网络控制的机器人视觉伺服系统[J].科学技术与工程,2008,7(23):6050-6054.

[4] MON YI JEN,LIN CHIN MIN.Supervisory Fuzzy Gaussian Neural Network Design for Mobile Robot Path Control[J].International Journal of Fuzzy Systems,2013,15(2):142-148.

[5] WATANABE K,TANG JLW,NAKAMURA M,et al.Mobile Robot Control Using Fuzzy-gaussian Neural Networks[G]//Intelligent Robots and Systems' 93,IROS'93.Proceedings of the 1993 IEEE/RSJ International Conference on.IEEE,1993:919-925.

[6] 贾松敏,高立文,樊劲辉,等.模糊神经网络在智能轮椅避障中的应用[J].华中科技大学学报:自然科学版,2013(5):77-81.

[7] 高彩霞,王福忠,赵悦冰.永磁直线电机遗传算法模糊神经网络失步预防策略[J].河南理工大学学报:自然科学版,2013,32(5):587-591.

[8] 钱夔,宋爱国,章华涛,等.基于自适应模糊神经网络的机器人路径规划方法[J].东南大学学报:自然科学版,2012,42(4):637-642.

[9] 杨丽,任淑艳,段海龙,等.基于模糊神经网络的不确定机器人实时轨迹跟踪控制的研究[J].现代科学仪器,2012(3)：6.

[10] 熊开封,张华.基于改进型FNN的移动机器人未知环境路径规划[J].制造业自动化,2013,35(22):1-4.

[11] FAN JINHUI,JIA SONGMIN,LI XIUZHI,et al.Motion Control of Intelligent Wheelchair Based on Sitting Postures[G]//Mechatronics and Automation (ICMA),2011 International Conference on.IEEE,2011:301-306.

[12] 樊劲辉,贾松敏,李秀智.基于RBF神经网络的全向智能轮椅自适应控制[J].华中科技大学学报:自然科学版,2014(2):111-115.

责任编辑：金 欣

An FGRBF-based mobile robot tracking control of neural network

LU Wei1, FAN Jin-hui2, ZHANG Hong-rui3

(1.Department of Computer Engineering, Shijiazhuang Medical College, Shijiazhuang, Hebei 050071, China; 2.School of Electrical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei, 050018, China; 3.Department of Information Technology, Shijiazhuang Vocational Technology Institute, Shijiazhuang, Hebei 050081, China)

In conventional fuzzy neural network based on S-type function, the number of nodes at the corresponding intermediate layer grows with the fuzzy rule number.An optimized fuzzy Gauss function neural network controller is discussed in this paper.Both the structure and the controller designing method are detailed.This optimized fuzzy neural network reduces the number of intermediate lays, and the real-time computation ability is guaranteed.Finally, the optimized algorithm is applied on a mobile robot, and the simulation results of tracking control has verified the real-time, effectiveness and feasibility of the method.

fuzzy neural network; FGRBF; mobile robot; tracking control

2015-05-01

2011年度河北省科技支撑计划项目(112035131D);2015年度河北科技大学通用航空平台项目

陆 薇(1979-)，女，河北定州人，石家庄医学高等专科学校讲师，研究方向：计算机技术及应用.

1009-4873(2015)04-0021-05

TP242.6

A