关于二面体群的共轭类长素图
2015-03-03张晓盼
张晓盼
(沈阳工业大学 研究生基础数学,辽宁 沈阳 110870)
关于二面体群的共轭类长素图
张晓盼
(沈阳工业大学 研究生基础数学,辽宁 沈阳 110870)

有限群;共轭类长素图;二面体群
有限群理论无论从理论本身还是实际应用来说都占据着突出的地位[1].观察有限群的发展历史可以知道,有限群的一些数量信息与其结构紧密相连.在有限群理论的研究中,关于群的共轭类长的素因子相关的一些算数特性与该群的性质和结构具有什么样的关系,这一直都是群论研究中非常重要的一个课题[2].下面就用共轭类长素图来描述二面体群的结构.
1 问题描述
1.1 符号说明
以下规定:图Γ*是由有限非空集合V及其二元子集E构成,其中V中元素称为顶点,E中元素称为边;集合V和E分别称为顶点集和边集.u,v∈V,如果u和v在图中有边,就称u和v在图中是邻接的;如果图Γ*的任何两个不同的顶点都是邻接的,则称Γ*是完全的;如果Γ*包含一条u-v路,那么就称u和v是连通的;如果对于Γ*中每对不同顶点u,v,Γ*都包含一条u-v路,那么Γ*为连通的;若Γ*的一个连通子图不是Γ*的其他任何连通子图的真子图,则称它为Γ*的一个连通分支,那么图Γ*称为不连通的;n(Γ*)表示类长素图的连通分支.连通图Γ*的所有顶点之间的最大距离称为Γ*的直径,记为diam(Γ*);类长图Γ*中,与顶点v相关联的边的总数称为是v的度,记为degΓ(v);度为0的顶点为孤立点;类长图Γ*中一个团是指图Γ*的一个完全子图.图Γ*中最大团的阶数称为Γ*的团数,记为ω(Γ*)[3].
1.2 相关定义及引理
定义1[4]对于有限群G中任意的两个元素a,b,我们称其在G中是共轭的,如果有另一元素g∈G,使得ag=b成立.这样,我们就可以把群G中的元素按照共轭的关系划分为k个都不相交的等价类,这个等价类叫共轭类.任一共轭类Ci中所包含元素的个数|Ci|叫做这个共轭类Ci的长度.
定义2 类长素图Γ*(G)是满足下面条件的无向图:
1)以ρ*(G)中的素数为顶点;
2)如果两个顶点p和q之间有一条边相连,当且仅当这两个素数的乘积pq整除Cl(G)中的某一元素b.
引理1[5]如果p,q是共轭类长素图的两个不相邻的顶点,则群G要么是p-幂零群要么是q-幂零群,NG(P)=CG(P)或者NG(Q)=CG(Q)其中P∈Sp(G)Q∈Sq(G).
引理2[6] 有限群G,则有1)共轭类长素图的连通分支n(Γ*(G))最多是2.2)如果n(Γ*(G))=2,则G为可解群.3)如果G是非交换的单群,则n(Γ*(G))=1;群G,如果共轭类长素图Γ*是不连通的当且仅当群G是拟-Frobenius群,有可交换的核和补.
引理3[7]可解群G,如果共轭类长素图有两个连通分支,而且n和N表示两个连通分支里两个素因子的阶(n≤N),则N≥2n-1.
引理4[8]如果p是一个给定的素数且整除每个(不等于1的)共轭类长度, 那么CG(P)≤Z(G),此处P是G的Sylowp-子群.
下面将讨论二面体群的共轭类长素图情况.
1.3 主要结论
我们记二面体群为D2n,设n≥3,定义:
设D2n是二面体群且n≥3,则D2n的共轭类如下:
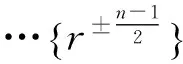
2)当n为偶数时:
上面给出的二面体群从n≥3开始,但二面体群存在共轭类长素图是从n≥5开始.
结论1 对于二面体群D2n,n≥5,当n为奇数时,那么非中心的共轭类长为{2,n},图1至5是二面体群共轭类长素图,图中孤立点指“2”,m表示n的素因子个数.
以此类推,二面体群有m个素因子对应的类长素图是有两个连通分支的非连通图,两个连通分支分别为完全图和孤立点.
结论2 对于二面体群D2n,n≥5,当n为奇数时,n的素因子个数设为m.则有以下结论:
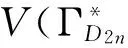


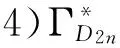








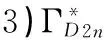
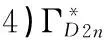



2 结论

[1] 张远达.有限群构造(上册)[M].北京:科学出版社,1982
[2] A.Beltran,M.J.Felipe.Corrigendum:Some class size conditions implying solvability of finite groups[J].Journal of Group Theory,2011,14:783-784
[3] 范益政,汪 毅.图论导引[M].北京:人民邮电出版社,2007
[4] 徐明曜.有限群导引(上册)(第二版)[M].北京:科学出版社,1999
[5] N.Ito,On finite groups with given conjugate types I[J].Nagoya Math.J,1953(6):17-28
[6] G.Alfandary,On graphs related to conjugacy classes of groups[J].Isreal J.Math,1994(86):211-220
[7] M.L.Lewis,An overview of graphs associated with character degeres and conjugacy class sizes in finite groups[J].Math,2008(38):175-211
[8] D.Chillag,M.Herzog.On the length of the conjugacy classes of finite group[J].Journal of Algebra,1990,131(1):110-125
Prime Graph Related to Conjugacy Classes of Dihedral Groups
Zhang Xiaopan
(Shenyang Industrial University Graduate, Shenyang 110870, China)
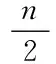
finitegroup;primegraphofconjugacyclasssizes;dihedralgroups
2015-02-21
张晓盼(1989-),女,河北邯郸人,在读硕士生.
1672-2027(2015)02-0021-03
O152
A
