择偶模型

赵 娜

(长治医学院 数学教研室，山西 长治 046000)

择偶模型

赵 娜

(长治医学院 数学教研室，山西 长治 046000)

通过调查问卷了解男女两性在择偶观上的不同,具体分析择偶过程中各因素的影响,建立FAHP模型,结合模糊综合评价法将复杂择偶决策过程量化,给出决策依据,做出定量评价,此模型还可以适用于其他多种实际情况和领域．

恋爱结婚；数学模型；层次分析法；模糊综合评价

0 问题背景

随着社会的进步和文明程度的提高,现代人的婚恋观发生了巨大变化,“剩男”“剩女”现象也越来越严重,难道真爱真的如此难以寻觅?众多机构的婚恋报告均显示,恋爱结婚一方面与个人的择偶观有着直接关系,另一方面与家庭、工作、生活圈等客观因素有着密不可分的联系．具体来说,男女双方最终能否走到一起主要取决于彼此感觉、个人品性、个人能力以及经济基础四个方面,而男女双方对于各方面的需求侧重不一．一般来说,男性更注重个人感觉与个人品性,女性更注重个人能力与经济基础．文[2-3]从不同角度对此问题进行了研究,均给出了一些实用性意见．文[2]给出了一种实用概率分布,文[3]考虑了同性竞争因素和家长影响因素下男生追女生问题,并建立了微分方程模型．

层次分析法(AHP)是一种定性分析和定量分析相结合的系统分析方法,是对具有较大规模评价因素的目标问题实现定量与定性分析相结合的有效决策方法,通过明确问题,建立层次分析结构模型,构造判断矩阵,层次单排序和层次总排序五个步骤计算各层次构成要素对于总目标的组合权重,从而得到不同可行方案的综合评价值,为选择最优方案提供依据,具有系统、实用、简洁等优点[4]．AHP的关键环节是构造一致判断矩阵,它直接影响到模型的效果,当目标因子数量较大时,检验判断矩阵一致性的计算复杂程度会很高,不一致时还需不断重复调整、检验进行修正．为此,模糊层次分析方法(FAHP)应运而生,很好地解决了此问题,提高了分析决策的准确性和合理性[5]．模糊综合评价法是一种基于模糊数学的综合评价方法,是对受多种因素影响的事物做出全面评价的一种有效决策方法,根据模糊数学的隶属度理论把定性评价转化为定量评价,其评价结果不是绝对的肯定或否定,而是以一个模糊集合来表示,具有系统性强、结果清晰等优点[6]．本文建立FAHP模型,具体分析了择偶过程中各方面因素的影响,并结合模糊综合评价方法将复杂的择偶评价决策思维过程量化,最终对择偶问题做出定量的综合评价．

1 数学模型

1.1 多层次模型结构的构建

利用FAHP法对择偶过程进行具体细致分析,建立如图1的多层次结构模型,模型分为4层:A目标层(择偶),B内容层(男方意愿,女方意愿),C准则层(感觉,品性,能力,经济基础),D子准则层(外貌,年龄,性情,心地,智商,情商,工作,家庭)．由准则层C和子准则层D之间各指标相互影响的关系来看,这是一个不完全层次结构模型．择偶问题是个双方互评的结构体系,所谓择偶成功即男女双方意愿均得到满足,内容层B对于目标层A的权重均为0.5．

2 判断矩阵的确定

根据表1对各指标进行两两比较,构造出模糊一致判断矩阵R=(rij)n×n．

3 层次单排序

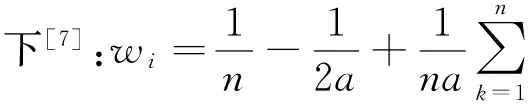
4 层次总排序

由各指标权重层层递进计算出子准则层D对于内容层B的组合权重W．

5 模糊综合评价

在双方互评过程中,对于各指标的评价多是模糊性的,我们采用模糊综合评价法[6],建立评语集V={很好，好，一般，差}={0.9,0.7,0.5,0.3},归一化V={0.375,0.292,0.208,0.125},对各指标分别给出评语vi构造出模糊评价矩阵Ψ=(vi),通过加权运算计算W⊗Ψ,得出综合评价．

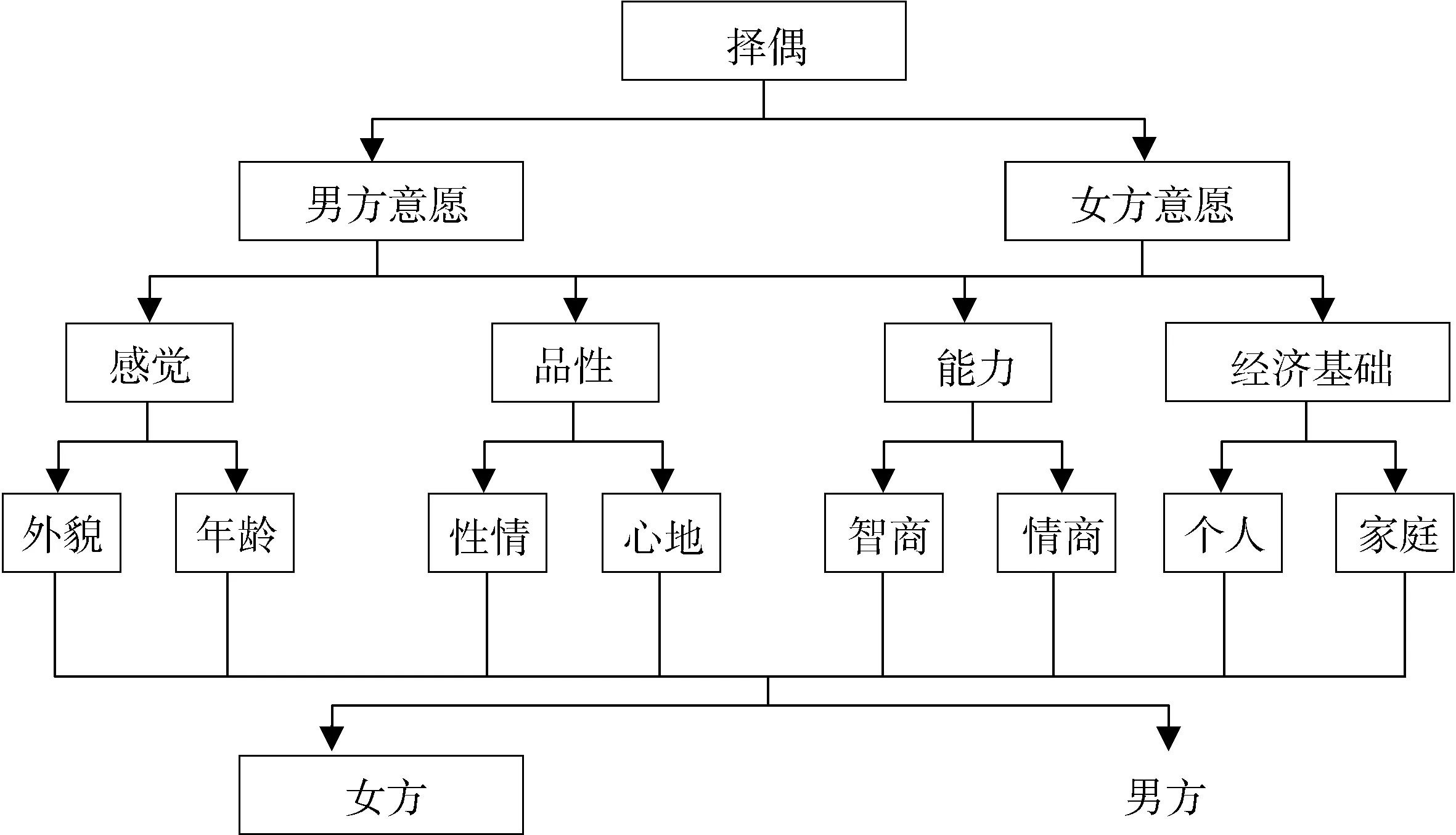
图1 多层次结构模型

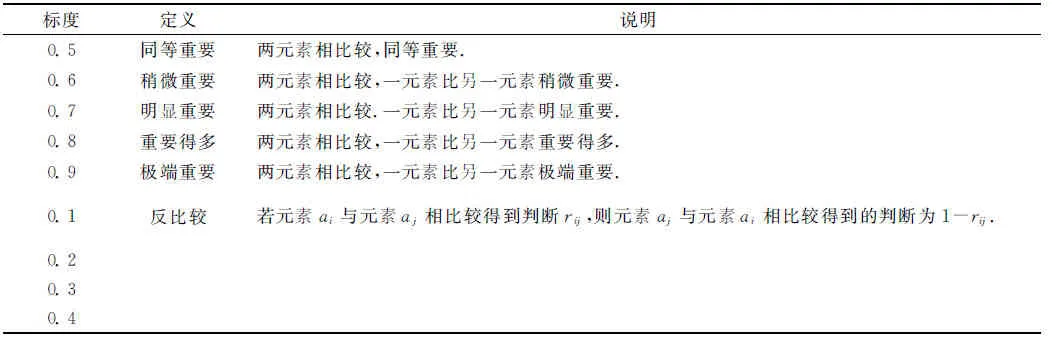
表1 标度

6 数值模拟

我们通过调查问卷分别对影响男女两性择偶各因素的重要性进行调查,即由他们为准则层C以及子准则层D各指标的重要性进行评分,得到如表2、表3模糊一致判断矩阵,并计算出其权重．

表2 模糊一致矩阵及权重(男)

C3D5D6权重D50.50.20.2D60.80.50.8

C2D3D4权重D30.50.60.6D40.40.50.4

C4D7D8权重D70.50.70.7D80.30.50.3

B1C1C2C3C4权重C10.50.40.80.70.3167C20.60.50.80.70.3500C30.20.20.50.40.1333C40.30.30.60.50.2000

表3 模糊一致矩阵及权重(女)

C3D5D6权重D50.50.70.7D60.30.50.3

C2D3D4权重D30.50.40.4D40.60.50.6

C4D7D8权重D70.50.70.7D80.30.50.3

B2C1C2C3C4权重C10.50.60.30.20.1833C20.40.50.40.40.2000C30.70.60.50.60.3167C40.80.60.40.50.3000

从表2、表3可以看出男女两性在择偶观念上的差异,并可以计算出子准则层D对于内容层B的组合权重:W男=(0.221 7,0.095 0,0.210 0,0.140 0,0.026 7,0.106 6,0.140 0,0.060 0),W女=(0.110 0,0.073 3,0.080 0,0.120 0,0.221 7,0.095 0,0.210 0,0.090 0)．假定现有一对未婚男女经过一段时间的相互了解,对彼此子准则层D各指标给出如下模糊评语:V男={很好,好,一般,很好,很好,差,好,一般},V女={一般,好,差,好,很好,好,很好,一般},通过计算可以得出男女双方彼此之间的综合评价:B1=0.283 8,B2=0.297 7．从数值上看,男女双方互评较低,恐难以满足各自意愿,择偶失败．

7 模型评价与改进

本模型为择偶问题提供了一种思维决策方式,将择偶的复杂过程简洁化、量化,最终给出了决策依据,简单易懂,还可以适用于其他多种实际情况和领域．

爱情总是让人盲目的,实际情况更复杂多变．在数值模拟中,我们给出的只是一种统计情形,考虑的指标较粗略,较少,实际情形所需考虑的因素远比本模型所涉及的多而细,比如还有距离、学历、甚至身高等等,特别地,还有父母．如果说恋爱是两个人的事,那么婚姻绝对是两家人的事．父母作为我们生命中最重要的人,他们的意见起着至关重要的作用,没有父母祝福的婚姻是不幸的．况且,父母作为旁观者一方面能更客观地作出评价,另一方面也会因考虑问题角度的不同评价会更全面．细化本模型,这些因素需要全面考虑在内,并会由个人差异得到不同权重．在数值模拟中,我们也假定了男女双方均是理智的,很清楚自己所想所需,而实际情况并非如此．在恋爱的过程中,彼此就像一面镜子,让对方更了解的同时也会更清楚自身条件,各指标权重随之改变,加之时间造成的情感因素,彼此在对方心中位置的改变,都会给最终的决策带来更多困难．任何事情不可能十全十美,面临抉择要懂得取舍,幸福掌握在自己手中．参考文献：

[1] 姜房源，金 星，叶 俊.数学模型.3版.北京:高等教育出版社，2003

[2] 宋占杰,李翠香,郭顺生.择偶问题的一种实用概率分布.数学的实践与认识,2002,32(5):783-785

[3] 周 星,克居正.男生追女生的数学模型.数学的实践与认识,2012,42(12):1-8

[4] 王莲芬,许树柏.层次分析法引论.北京:中国人民大学出版社,1990

[5] 张吉军.模糊层次分析法.模糊系统与数学,2000,14(2):80-88

[6] 谢季坚,刘承平.模糊数学方法及其应用.2版.武汉:华中科技大学出版社,2004

[7] 吕跃进.基于模糊一致矩阵的模糊层次分析法的排序.模糊系统与数学,2002(6):80-86

Mate Selection Model

ZHAO Na

(Mathematics Teaching and Research Group, Changzhi Medical College, Changzhi 046000, China)

To understand the gender differences in mate choice through the questionnaire investigation and detailed analysis the different effects of various factors in mate selection process, we establish FAHP model and combine with fuzzy comprehensive evaluation method to simplify the complex decision process, to provide a basis for decision-making and make quantitative evaluation. This model can also be applied to other situations and fields.

marry；mathematical model；FAHP；fuzzy comprehensive evaluation

2015-09-28

赵 娜(1982-)，女，长治医学院数学教研室讲师，主要从事数学建模及数学教学研究.

1672-2027(2015)04-0023-03

O29

A